Lý thuyết, cách xác định và bài tập các trường hợp đường tròn nội tiếp

Đường tròn nội tiếp

I. Lý thuyết

Đường tròn nội tiếp

a) Khái niệm

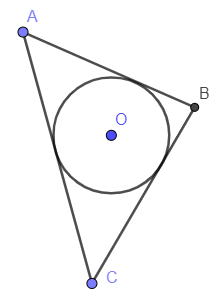
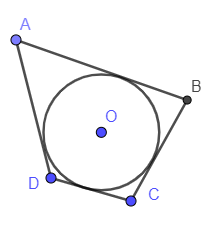
- Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác.

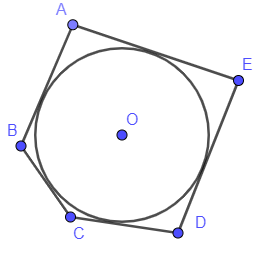Cách hình vẽ trên thể hiện đường tròn nội tiếp tam giác, đường tròn nội tiếp tứ giác, đường tròn nội tiếp ngũ giác.

b) Cách xác định đường tròn nội tiếp đa giác

Tâm đường tròn nội tiếp đa giác là giao của các đường phân giác của tất cả các góc trong đa giác.

Để xác định đường tròn nội tiếp đa giác ta làm như sau:

Bước 1: Kẻ các đường phân giác của các góc rồi xác định giao điểm của chúng.

Bước 2: Kẻ đường thẳng đi qua giao điểm và vuông góc với một cạnh bất kỳ để xác định bán kính.

Chú ý: Một đa giác chỉ có đường tròn nội tiếp khi các đường phân giác của các góc của đa giác đồng quy.

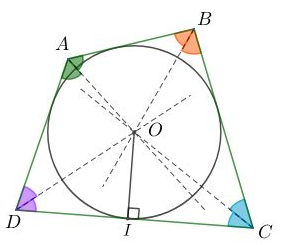
Cho tứ giác ABCD, vẽ phân giác các góc của tứ giác, các đường thẳng này đồng quy tại O do đó (O; OI) là đường tròn nội tiếp tứ giác ABCD với I là hình chiếu của O lên DC.

3. Một số định lí

- Bất kỳ đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

- Tâm của đường tròn nội tiếp và tâm của đường tròn ngoại tiếp đa giác đó trùng nhau thì đa giác đó là đa giác đều và tâm đó chính là tâm của đa giác đều.

II. Dạng bài tập

Dạng 1: Xác định tâm và bán kính đường tròn nội tiếp

Ví dụ 1: Cho một đường tròn bán kính r nội tiếp trong tam giác vuông cân ABC vuông cân tại A và một đường tròn bán kính R ngoại tiếp tam giác ấy. Tính $\frac{R}{r}$.

Lời giải:

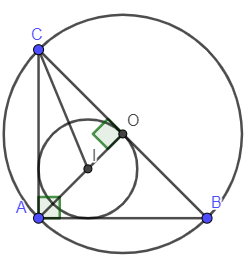
Gọi I là tâm đường tròn nội tiếp tam giác ABC.

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.

Giả sử tam giác ABC vuông cân tại A có cạnh góc vuông AB = AC = a

Xét tam giác vuông ABC vuông tại A ta có:

$A{B}^2+A{C}^2=B{C}^2$

$\iff a^2+a^2=B{C}^2$

$\iff B{C}^2=2a^2$

$\Rightarrow BC=\sqrt{2}a$

Vì ABC là tam giác vuông tại A do đó tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền (định lí)

Do đó O là trung điểm của BC

$\Rightarrow R=OB=\frac{BC}{2}=\frac{\sqrt{2}a}{2}$

Vì ABC là tam giác vuông cân tại A do đó AO là đường trung tuyến cũng là đường phân giác, đường cao của tam giác ABC

=> A, I, O thẳng hàng và $AO\perp BC$

Ta có AO = $\frac{\sqrt{2}a}{2}$ (do O là tâm đường tròn ngoại tiếp tam giác ABC).

Xét tam giác AOC có:

CI là đường phân giác của $\widehat{C}$ và CI cắt AO tại I nên ta có:

$\frac{CA}{CO}=\frac{AI}{OI}$ (tính chất đường phân giác trong tam giác)

$\iff \frac{a}{\frac{\sqrt{2}a}{2}}=\frac{AI}{OI}$

$\iff \frac{AI}{OI}=\sqrt{2}$

$\iff AI=\sqrt{2}OI$

Mà $AI+OI=AO$

$\Rightarrow \sqrt{2}OI+OI=\frac{\sqrt{2}a}{2}$

$\iff OI\left(\sqrt{2}+1\right)=\frac{\sqrt{2}a}{2}$

$\iff OI=\frac{2-\sqrt{2}}{2}a$

Vậy r = $\frac{2-\sqrt{2}}{2}a$

$\Rightarrow \frac{R}{r}=\frac{\frac{\sqrt{2}}{2}a}{\frac{2-\sqrt{2}}{2}a}=1+\sqrt{2}$.

Ví dụ 2: Cho đờng tròn (O; R) và điểm M nằm ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA và Mb với đường tròn (O). Qua M kẻ cát tuyến MCD không đi qua tâm O cắt đường tròn tại hai điểm C và D sao cho C nằm giữa M và D. Gọi I là trung điểm của dây CD. Khi đó MAOIB có là ngũ giác nội tiếp hay không? Nếu có hãy xác định tâm và bán kính của đường tròn đó.

Lời giải:

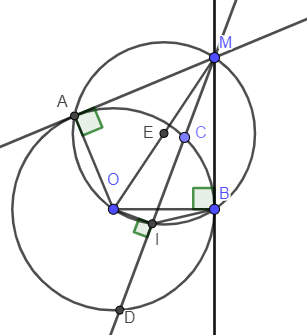
Vì MA là tiếp tuyến của đường tròn (O), A là tiếp điểm nên MA vuông góc với OA.

$\Rightarrow \widehat{MAO}=90°$

Vì MB là tiếp tuyến của đường tròn (O), B là tiếp điểm nên MB vuông góc với OB.

$\Rightarrow \widehat{MBO}=90°$

Vì I là trung điểm của CD nên OI vuông góc với CD (tính chất)

$\Rightarrow \widehat{MOI}=90°$

Gọi trung điểm của MO là E.

Tam giác OAM vuông tại A với E là trung điểm của MO

$\Rightarrow OE=EM=AE=\frac{1}{2}MO$ (định lí đường trung tuyến ứng với cạnh huyền) (1)

Tam giác OBM vuông tại B với E là trung điểm của MO

$\Rightarrow OE=EM=BE=\frac{1}{2}MO$ (định lý đường trung tuyến ứng với cạnh huyền) (2)

Tam giác OIM vuông tại I có E là trung điểm của MO

$\Rightarrow OE=ME=IE=\frac{1}{2}MO$ (định lí đường trung tuyến ứng với cạnh huyền) (3)

Từ (1); (2); (3) $\Rightarrow OE=EM=IE=AE=BE=\frac{1}{2}MO$

Hay 5 điểm A, B, M, I, O cách đều điểm E.

Hay ngũ giác AOIBM nội tiếp đường tròn (E; OE) với E là trung điểm của MO.

Dạng 2: Tính các đại lượng liên quan đến đa giác nội tiếp ngoại tiếp

Phương pháp giải: Ta sử dụng một số khái niệm công thức sau:

- Bán kính đường tròn ngoại tiếp đa giác là khoảng cách từ tâm đường tròn đến một đỉnh bất kỳ của đa giác đó.

- Bán kính đường tròn nội tiếp đa giác là khoảng cách từ tâm đường tròn đến một cạnh bất kỳ của đa giác đó.

- Cho đa giác n – cạnh đều có cạnh bằng a ta có:

+ Chu vi đa giác là: c = n.a (đơn vị độ dài).

+ Mỗi góc ở đỉnh của đa giác có số đo là $\frac{\left(n-2\right).180°}{n}$.

+ Mỗi góc ở tâm của đa giác có số đo là $\frac{360°}{n}$.

+ Bán kính đường tròn ngoại tiếp: $R=\frac{a}{2\sin \frac{180°}{n}}\Rightarrow a=2R.\sin \frac{180°}{n}$.

+ Bán kính đường tròn nội tiếp: $r=\frac{a}{2\tan \frac{180°}{n}}\Rightarrow a=2r.\tan \frac{180°}{n}$.

+ Diện tích đa giác đều: $S=\frac{1}{2}n.a.r$(đơn vị diện tích).

Ví dụ 1: Tính diện tích hình lục giác đều có cạnh bằng a?

Lời giải:

Vì là hình lục giác đều nên ta có n = 6

Bán kính đường tròn nội tiếp lục giác đều có cạnh bằng a là:

$r=\frac{a}{2.\tan \frac{180°}{n}}=\frac{a}{2.\tan \frac{180°}{6}}$

$\iff r=\frac{a}{2.\tan 30°}=\frac{a}{2.\frac{\sqrt{3}}{3}}=\frac{\sqrt{3}a}{2}$ (đơn vị độ dài)

Áp dụng công thức ta có diện tích hình lục giác đều có cạnh bằng a là:

S = $\frac{1}{2}n.a.r$= $\frac{1}{2}6.a.\frac{\sqrt{3}a}{2}=\frac{3\sqrt{3}{a}^2}{2}$ (đơn vị diện tích)

Ví dụ 2: Cho tam giác ABC cân tại A, có $\widehat{BAC}=120°$ và BC = 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

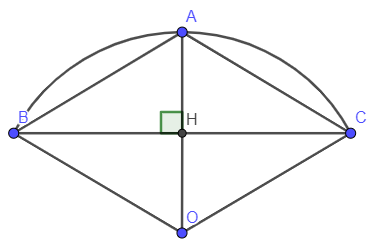
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, H là giao điểm của OA và BC.

Xét tam giác OAC, có OA = OC => tam giác OAC cân tại O.

Ta có tam giác ABC cân tại A => AO là đường trung trực của tam giác cũng là đường phân giác của tam giác

$\Rightarrow \widehat{CAO}=\widehat{BAO}=\frac{\widehat{BAC}}{2}=\frac{120°}{2}=60°$

Do đó tam giác OAC là tam giác đều

Đặt OA = OC = AC = x

Vì OA là đường trung trực của BC nen H là trung điểm của BC.

=> BH = CH = $\frac{BC}{2}=\frac{6}{2}=3cm$

Vì CH vuông góc với OA nên CH cũng là đường trung tuyến nên H là trung điểm của AO

$\Rightarrow AH=OH=\frac{OA}{2}=\frac{x}{2}\left(cm\right)$

Xét tam giác ACH vuông tại H ta có:

$A{C}^2=A{H}^2+C{H}^2$(định lý Py – ta – go)

$\iff x^2={\left(\frac{x}{2}\right)}^2+3^2$

$\iff x^2=\frac{x^2}{4}+9$

$\iff x^2-\frac{x^2}{4}=9$

$\iff \frac{3x^2}{4}=9$

$\iff x^2=9:\frac{3}{4}$

$\iff x^2=12$

$\iff x=2\sqrt{3}$ cm.

Dạng 3: Chứng minh tứ giác ngoại tiếp đường tròn

Phương pháp giải:

- Một tứ giác là tứ giác ngoại tiếp đường tròn khi và chỉ khi các đường phân giác trong của các góc đồng quy tại một điểm.

- Tứ giác có tổng các cặp cạnh đối bằng nhau là tứ giác ngoại tiếp.

Ví dụ 1: Chứng minh tứ giác ABCD ngoại tiếp đường tròn khi và chỉ khi AB + CD = AD + BC.

Lời giải:

* Chứng minh chiều thuận: Nếu ABCD ngoại tiếp đường tròn thì AB + CD = AD + BC

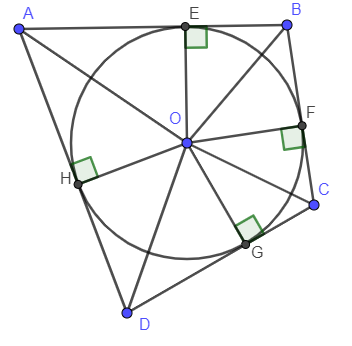
Gọi O là tâm đường tròn nội tiếp tứ giác ABCD. Vẽ OE, OF, OG, OH theo thứ tự vuông góc với AB, BC, CD, AD tại E, F, G, H.

Vì OE vuông góc với AB và (O) tiếp xúc với AB tại E nên AB là tiếp tuyến của đường tròn (O)

Vì OF vuông góc với BC và (O) tiếp xúc với BC tại F nên BC là tiếp tuyến của đường tròn (O).

Hai tiếp tuyến AB và BC cắt nhau tại B do đó BE = BF (tính chất) (1)

Chứng minh tương tự ta được CF = CG; DG = DH; AH = AE (2).

Ta có: AE + EB = AB (3)

BF + CF = BC (4)

CG + GD = CD (5)

AH + DH = AD (6)

Từ (1); (2); (3); (4); (5); (6) $\Rightarrow AB+CD=AD+BC$.

* Chiều ngược lại: Nếu AB + CD = AD + BC thì tứ giác ABCD là tứ giác ngoại tiếp.

- Nếu AB = AD thì CD = CB.

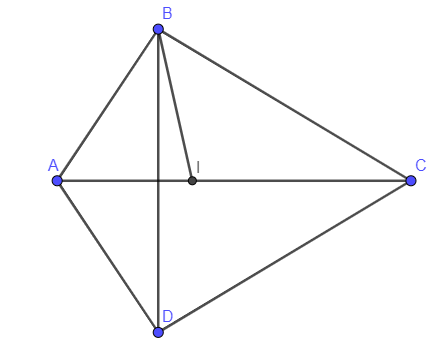
Khi đó giao điểm I của AC với đường phân giác trong của góc B chính là tâm đường tròn nội tiếp tứ giác ABCD. Ta có điều phải chứng minh.

- Không mất tính tổng quát ta xem AB > AD.

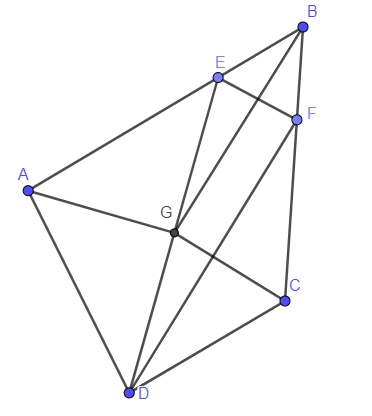
Vì AB + CD = AD + CB nên BC > CD.

Do đó tồn tại các điểm E và F theo thứ tự trên AB, BC sao cho AE = AD, CF = CD.

Ta có: AB + CD = AD + CB

=> AE + BE + CD = AD + CF + FB

=> BE = FB.

Ta có:

Tam giác ADE cân tại A do AD = AE

Tam giác BEF cân tại B do BE = BF

Tam giác CFD cân tại C do CF = CD.

Vì tam giác ADC cân tại A nên đường phân giác góc A cũng là đường trung trực của ED.

Vì tam giác BEF cân tại B nên đường phân giác góc B cũng là đường trung trực của EF.

Vì tam giác CFD cân tại C nên đường phân giác góc C cũng là đường trung trực của FD.

Mà ba điểm E, F, D không thẳng hàng nên E, F, D tạo thành một tam giác.

=> ba đường trung trực của EF, ED, FD đồng quy

Hay ba đường phân giác của ba góc của tứ giác ABCD đồng quy.

Do đó tứ giác ABCD là tứ giác ngoại tiếp.

Ví dụ 2: Cho hình thang ABCD vuông tại A và D. Biết AB = 10cm, BC = 13cm, CD = 15cm. Chứng minh hình thang ABCD ngọa tiếp đường tròn, tìm bán ính đường tròn đó.

Lời giải:

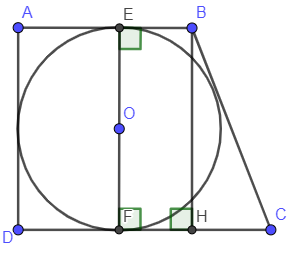
Vì ABCD là hình thang vuông tại A và D $\Rightarrow \widehat{A}=\widehat{D}=90°$

Vẽ BH vuông góc với CD tại H $\Rightarrow \widehat{BHD}=90°$.

Xét tứ giác ABHD có:

$\Rightarrow \widehat{A}=\widehat{D}=\widehat{BHD}=90°$

=> tứ giác ABCD là hình chữ nhật.

$\Rightarrow AB=DH=10cm$

Lại có: DH + CH = CD mà CD = 15cm nên CH = 5cm.

Xét tam giác BHC vuông tại H ta có:

$B{H}^2+C{H}^2=B{C}^2$(định lý Py – ta – go)

$\iff B{H}^2+5^2={13}^2$

$\iff B{H}^2+25=169$

$\iff B{H}^2=169-25$

$\iff B{H}^2=144$

$\iff BH=12cm$

Mà ABHD là hình chữ nhật nên AD = BH = 12cm.

Xét hình thang ABCD có:

AB + CD = 10 + 15 = 25cm

AD + BC = 12 + 13 = 25cm

Do đó: AB + CD = AD + BC.

=> hình thang ABCD ngoại tiếp đường tròn.

Gọi O là tâm đường tròn nội tiếp hình thang ABCD, do đo O các đều AB và CD.

Vẽ OE vuông góc với AB; OF vuông góc với CD. Do AB // CD nên O, E, F thẳng hàng hay EF = BH = 12cm

Lại có OE = OF nên OE = OF = 6cm.

Vậy bán kính đường tròn nội tiếp hình thang ABCD là 6cm.

III. Bài tập tự luyện

Bài 1: Các đường cao AD, BE của tam giác ABC cắt nhau tại H (góc C khác góc vuông) và cắt đường tròn (O) ngoại tiếp tam giác ABC lần lượt tại I và K.

a) Chứng minh tứ giác CDHE nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác đó.

b) Chứng minh tam giác CKI cân.

Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Ba đường cao của tam giác là AF, BE, CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác.

Bài 3: Cho tam giác ABC vuông tại A có AB < AC, đường cao AH (H thuộc BC). Lấy điểm D sao cho H là trung đểm của BD. Gọi E là chân đường vuông góc hạ từ C xuống đường thẳng AD. Chứng minh tứ giác AHEC nội tiếp và xác định vị trí tâm O của đuờng tròn ngoại tiếp tứ giác đó.

Bài 4: Cho ngũ giác đều có cạnh bằng a

a) Tính chu vi và diện tích ngũ giác đều đó.

b) Tính số đo mỗi góc của ngũ giác đều.

Bài 5: Cho tứ giác ABCD ngoại tiếp đường tròn, biết rằng các tia AB, CD cắt nhau tại E, các tia AD và BC cắt nhau tại F. Chứng minh rằng:

a) AE + CF = AF + CE.

b) BE + BF = DE + DF.

Bài 6: Cho hình thang ABCD (AB // CD) ngoại tiếp đường tròn (O). Tiếp điểm trên AB, CD theo thứ tự là E và F. Chứng minh rằng AC, BD, EF đồng quy.

Bài 7: Tính cạnh hình 12 cạnh đều theo bán kính đường tròn ngoại tiếp hình 12 cạnh đều đó.

Bài 8: Cho đường tròn (O) nội tiếp trong hình thang ABCD (AB // CD) tiếp xúc với cạnh AB tại E với cạnh CD tại F.

a) Chứng minh: $\frac{BE}{AE}=\frac{DF}{CF}$

b) Bết AB = a, CB = b (a < b), BE = 2.AE. Tính diện tích hình thang ABCD.

Bài 9: Cho tam giác ABC ngoại tiếp (O). Trên BC lấy M, trên BA lấy N, trên CA lấy P sao cho B = BN và CM = CP. Chứng minh rằng:

a) O là tâm đường tròn ngoại tiếp tam giác MNP.

b) Tứ giác ANOP nội tiếp đường tròn.

c) Tìm vị trí điểm M, N, P sao cho NP nhỏ nhất.

Bài 10: Cho đường (O; R) nội tiếp hình thang ABCD (AB // CD), với G là tiếp điểm của đyờng tròn (o; R) với các cạnh CD, biết AB = $\frac{4}{3}R$ và BC = $\frac{5}{2}R$. Tính tỉ số giữa GD và GC.

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Bài tập về góc có đỉnh nằm trong đường tròn, góc có đỉnh nằm ngoài đường tròn và cách giải

Cung chứa góc, các bài toán về quỹ tích, dựng hình và cách giải