Tổng hợp các công thức hình học phẳng lớp 6 và bài tập (có đáp án 2025)
Với tài liệu về Tổng hợp các công thức hình học phẳng lớp 6 và bài tập có đáp án bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.
Tổng hợp các công thức hình học phẳng lớp 6 và bài tập có đáp án
I. Công thức tính chu vi, diện tích hình tam giác
1. Lý thuyết
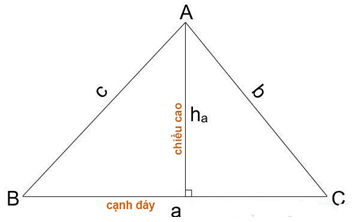
Cho tam giác ABC với độ dài 3 cạnh là BC = a; AC = b; AB = c và chiều cao ứng với cạnh a là h.
Chu vi tam giác là tổng độ dài ba cạnh của tam giác:
C = a + b + c (đơn vị độ dài)
Diện tích tam giác bằng một nửa tích của cạnh đáy nhân với chiều cao tương ứng.
S = 1/2. a . h (đơn vị diện tích)
* Đối với tam giác thường:
S = 1/2. a . h (đơn vị diện tích)
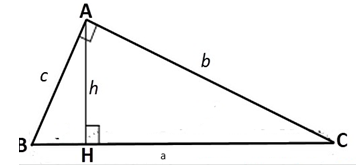
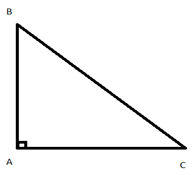
Đối với tam giác vuông:
Ngoài công thức tính diện tích tam giác như tam giác thường, để tính diện tích tam giác vuông ta có thể tính bằng cách lấy tích hai cạnh góc vuông rồi chia cho 2.
S = 1/2. a . h = 1/2. b. c (đơn vị diện tích)
Ví dụ 1. Tính diện tích tam giác biết chiều cao của tam giác đó là 5cm và độ dài cạnh đáy tương ứng là 8cm.
Hướng dẫn giải:
Diện tích tam giác là:
S = 1/2. 5. 8= 20(cm2)
Vậy diện tích tam giác là 20cm2.
Ví dụ 2. Cho tam giác ABC vuông tại A có các cạnh AB = 3cm; AC = 4cm và BC = 5cm. Tính chu vi và diện tích tam giác ABC.
Hướng dẫn giải:
Chu vi tam giác ABC là:
3 + 4 + 5 = 12 (cm)
Diện tích tam giác ABC là:
S = 1/2. 3. 4= 6 (cm2)
Vậy chu vi tam giác ABC là 12cm, diện tích tam giác ABC là 6cm2.
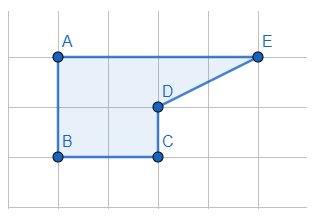
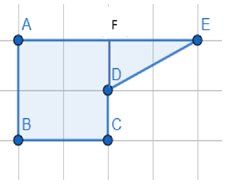
Ví dụ 3. Cho hình vẽ sau:
Tính diện tích phần hình được tô màu. (coi mỗi cạnh của 1 ô vuông nhỏ là 1dm)
Hướng dẫn giải:
Ta chia hình ban đầu thành hai hình: Hình vuông ABCF và hình tam giác DFE
Diện tích hình vông ABCF là:
SABFC = 2.2 = 4 (dm2).
Diện tích tam giác DEF là:
SDEF = 1/2.2.1 = 1 (dm2).
Vậy diện tích hình được tô màu là:
4 + 1 = 5 (dm)
2. Bài tập vận dụng
Bài 1. Tính diện tích tam giác có:
a) Độ dài cạnh đáy là 15cm và chiều cao là 12cm.
b) Độ dài đáy là 6cm và chiều cao là 4,5cm.
Bài 2. Tính diện tích tam giác vuông có:
a) Hai cạnh góc vuông lần lượt là 3cm và 4cm.
b) Hai cạnh góc vuông lần lượt là 6m và 8m.
Bài 3. Cho tam giác ABC đều có cạnh bằng 12 cm. Chiều cao của tam giác là 14cm. Tính chu vi, diện tích tam giác.
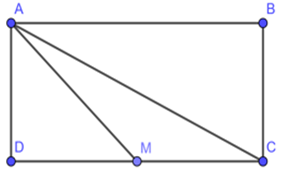
Bài 4. Cho hình chữ nhật ABCD có AD = 4cm, AB = 6cm. DM = 3cm, MC = 1cm.
a) Tính diện tích tam giác ADM?
b) Tính diện tích tam giác AMC?
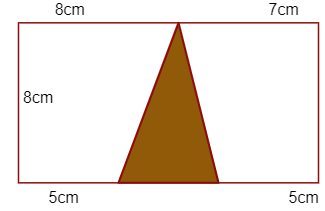
Bài 5. Tính diện tích phần được tô màu trong hình vẽ:
................................
................................
................................
II. Công thức tính chu vi, diện tích hình vuông
1. Lý thuyết
*Chu vi hình vuông là tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích. Để tính chu vi hình vuông, bạn cần biết chiều dài cạnh của hình vuông
Chu vi hình vuông được tính theo công thức: 4 lần chiều dài các cạnh của hình .
Trong đó:
-
P là chu vi hình vuông.
-
a là chiều dài các cạnh hình vuông.
Ví dụ: nếu chiều dài cạnh hình vuông là 6cm thì chu vi hình vuông đó sẽ là 4x6cm = 24cm.
*Diện tích hình vuông được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình vuông. Để tính diện tích hình vuông, bạn cần biết chiều dài cạnh của hình vuông.
Diện tích hình vuông bằng bình phương chiều dài cạnh hình vuông.
Trong đó:
-
S là diện tích hình vuông.
-
a là chiều dài các cạnh hình vuông.
-
Lưu ý: Đơn vị đo diện tích sẽ viết dưới dạng mũ 2 (2), đọc là "tên đơn vị + vuông". Ví dụ: m2 (mét vuông), cm2 (centimet vuông)...
Ví dụ: Để tính diện tích của hình vuông có cạnh là 6cm, bạn lấy 6x6 = 36cm2
2. Bài tập vận dụng
Bài 1:
Hình vuông ABCD có cạnh bằng 4 cm. Tính diện tích của hình vuông ABCD?
Giải:
Để tính diện tích của hình vuông ABCD, ta có thể sử dụng công thức: S = axa, trong đó a là độ dài cạnh của hình vuông.
Với hình vuông ABCD, a = 4 cm. Do đó, diện tích của hình vuông ABCD là:
S = axa = 4x4 = 16 cm2.
Câu trả lời cuối cùng là: 16 cm2.
Bài 2:
Cho hình vuông ABCD có chu vi bằng 28cm. Tính diện tích hình vuông ABCD.
Giải:
P = 4 x a => Chiều dài cạnh của hình vuông ABCD là: a = 28 : 4 = 7 cm
Diện tích hình vuông ABCD là: S = 7 x 7 = 49 cm²
Bài 3:
Một miếng đất hình vuông được mở rộng về 1 phía là 5cm thì ta có được chu vi hình chữ nhật là 110cm. Tính diện tích miếng đất sau khi mở rộng.
Giải:
Chu vi của miếng đất của hình vuông là: 110 - 5 x 2 = 100 cm
Cạnh của miếng đất hình vuông (cũng là chiều rộng của hình chữ nhật) là: 100 : 4 = 25 cm
Chiều dài miếng đất của hình chữ nhật là: 25 + 5 = 30 cm
Sau khi mở rộng thì diện tích miếng đất là 25 x 30 = 750cm2
III. Công thức tính chu vi, diện tích hình chữ nhật
1. Lý thuyết
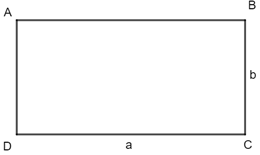
Cho hình chữ nhật ABCD có chiều dài và chiều rộng lần lượt là a và b.
- Chu vi của hình chữ nhật ABCD bằng 2 lần tổng chiều dài và chiều rộng, kí hiệu:
C = 2 . (a + b) (đơn vị độ dài)
- Diện tích của hình chữ nhật ABCD bằng tích của chiều dài và chiều rộng, kí hiệu:
S = a . b (đơn vị diện tích)
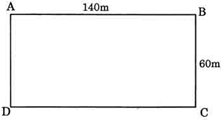
Ví dụ 1. Một thửa ruộng hình chữ nhật có chiều dài 140 m và chiều rộng 60 m.
a) Tính chu vi của thửa ruộng?
b) Tính diện tích của thửa ruộng?
Hướng dẫn giải:
a) Chu vi của thửa ruộng hình chữ nhật là:
2 . (140 + 60) = 400 (m).
b) Diện tích của thửa ruộng hình chữ nhật là:
140 . 60 = 8400 (m2).
Vậy chu vi thửa ruộng là 400m và diện tích thửa ruộng là 8 400m2.
Ví dụ 2. Một nền nhà hình chữ nhật có chiều dài 18m, chiều rộng 5m. Người ta dùng gỗ để lát sàn mỗi mét vuông hết 450 000. Hỏi để lát hết sàn của nền nhà đó thì hết bao nhiêu tiền gỗ?
Hướng dẫn giải:
Diện tích của nền nhà hình chữ nhật là:
18 . 5 = 90 (m2).
Số tiền gỗ phải bỏ ra để lát nền nhà là:
90 . 450 000 = 40 500 000 (nghìn đồng)
Vậy số tiền gõ phải bỏ ra để lát nền nhà là 40 500 000 đồng.
Ví dụ 3. Một hình chữ nhật có chiều rộng 12 cm, biết chu vi gấp 6 lần chiều rộng. Tính diện tích hình đó.
Hướng dẫn giải:
Chu vi của hình chữ nhật là:
12 . 6 = 72 (cm).
Nửa chu vi hình chữ nhật là:
72 : 2 = 36 (cm).
Chiều dài hình chữ nhật là:
36 – 12 = 24 (cm).
Diện tích hình chữ nhật là:
12 . 24 = 288 (cm2).
2. Bài tập vận dụng
Bài 1.
a) Tính chu vi hình chữ nhật có kích thước ghi trên hình vẽ;
b) Tính diện tích hình chữ nhật có kích thước ghi trên hình vẽ;
Bài 2.Tính chu vi và diện tích hình chữ nhật có chiều rộng 15 cm, chiều dài hơn chiều rộng 15 cm.
Bài 3. Một hình chữ nhật có chiều dài 60 cm, chiều rộng bằng chiều dài.
a) Tính chu vi, diện tích hình chữ nhật đó.
b) Chu vi gấp mấy lần chiều rộng.
Bài 4. Một thửa ruộng hình chữ nhật có chiều dài 24 m, chiều rộng 18 m. Trên thửa ruộng đó mỗi mét vuông thu hoạch được 5 kg rau. Hỏi cả thửa ruộng đó thu hoạch được bao nhiêu ki- lô- gam rau?
Bài 5. Một thửa ruộng hình chữ nhật có chiều dài 35 m, chiều rộng 22 m.Trên thửa ruộng đó 5 m2 thu hoạch được 15 kg dưa. Hỏi cả thửa ruộng đó thu hoạch được bao nhiêu kg dưa?
IV. Công thức tính chu vi, diện tích hình thang
1. Lý thuyết
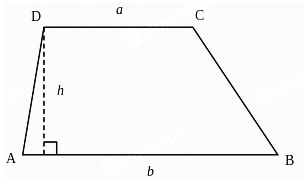
Cho hình thang ABCD có chiều dài 2 đáy lần lượt là DC = a và Ab = b, chiều cao h, BC = c, AD = d.
- Chu vi của hình thang bằng tổng độ dài của 4 cạnh xung quanh hình thang, kí hiệu:
P = a + b + c +d (đơn vị độ dài)
- Diện tích của hình thang bằng một nửa tổng của hai đáy nhân với đường cao, kí hiệu:
S = (đơn vị diện tích).
Ví dụ 1. Cho hình thang có độ dài hai cạnh đáy và hai cạnh bên lần lượt là 8 cm, 9 cm, 6 cm và 7 cm, đường cao 6 cm. Tính chu vi và diện tích của hình thang đó?
Hướng dẫn giải:
Chu vi của hình thang là:
8 + 9 + 6 + 7 = 30 (cm).
Diện tích của hình thang là:
6 . = 51 (cm2).
Vậy chu vi hình thang là 30cm, diện tích hình thang là 51cm2.
Ví dụ 2. Cho hình thang có hai cạnh đáy lần lượt là 6 cm và 4 cm. Chiều dài của hai cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?
Hướng dẫn giải:
Vì độ dài mỗi cạnh bên bằng nửa tổng độ dài hai đáy nên mỗi cạnh bên có độ dài là:
(6 + 4) : 2 = 5 (cm).
Chu vi của hình thang là:
6 + 4 + 5 + 5 = 20 (cm).
Vậy chu vi hình thang là 20cm.
Ví dụ 3. Cho hình thang có đáy lớn bằng 12 cm, đáy nhỏ bằng đáy lớn, chiều cao bằng 4 cm. Tính diện tích hình thang đó?
Hướng dẫn giải:
Độ dài đáy nhỏ là:
12 . = 8 (cm).
Diện tích của hình thang là:
4 . = 40 (cm2).
Vậy diện tích hình thang là 40cm2
2. Bài tập vận dụng
Bài 1. Cho hình thang có độ dài đáy nhỏ bằng 5 cm, đáy lớn bằng 10 cm. Chiều cao của hình thang bằng 6cm. Tính diện tích của hình thang đó?
Bài 2. Cho hình thang có hai cạnh đáy lần lượt là 12 cm và 8 cm. Chiều dài của cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?
Bài 3. Cho hình thang có tổng độ dài hai đáy là 45cm và gấp 3 lần chiều cao, tính diện tích hình thang đó?
Bài 4. Cho một thửa ruộng hình thang có đáy lớn bằng 120 m, đáy bé bằng đáy lớn. Đáy bé dài hơn chiều cao 5 m. Trung bình cứ 100 m2 thu hoạch được 64,5 kg thóc. Hãy tính số ki – lô – gam thóc thu hoạch được trên thửa ruộng đó?
Bài 5. Một mảnh vườn trồng táo hình thang có đáy lớn bằng 40 m, đáy bé bằng nửa đáy lớn. Độ dài cạnh bên thứ nhất của mảnh vườn là 10 m, độ dài cạnh bên thứ 2 gấp 3 lần độ dài cạnh bên thứ nhất. Tính chu vi mảnh vườn đó?
V. Công thức tính chu vi, diện tích hình bình hành
1. Lý thuyết
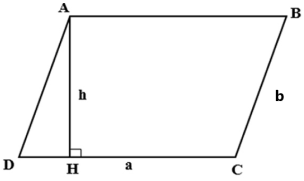
Cho hình bình hành ABCD có các cạnh lần lượt là AB = CD = a; BC = AD = b, đường cao AH = h.
- Chu vi hình bình hành là tổng độ dài các cạnh xung quanh hình bình hành, kí hiệu:
C = 2 . (a + b) (đơn vị độ dài)
- Diện tích hình bình hành: S = a . h (đơn vị diện tích)
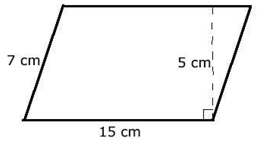
Ví dụ 1. Cho một mảnh giấy hình bình hành như hình vẽ:
a) Tính chu vi mảnh giấy?
b) Tính diện tích mảnh giấy?
Hướng dẫn giải:
a) Chu vi của mảnh giấy hình bình hành là:
2 . (15 + 7) = 44 (cm).
b) Diện tích của mảnh giấy hình bình hành là:
15 . 5 = 75 (cm2).
Vậy chu vi của mảnh giấy là 44cm và diện tích của mảnh giấy là 75cm2.
Ví dụ 2. Tính diện tích của một hình bình hành có độ dài đáy là 18 cm, chiều cao bằng độ dài đáy.
Hướng dẫn giải:
Chiều cao hình bình hành là:
18 . = 10 (cm).
Diện tích hình bình hành là:
10 . 18 =180 (cm2).
Vậy diện tích hình bình hành là 180 cm2.
Ví dụ 3. Chu vi hình bình hành bằng 48 cm. Tính độ dài các cạnh của hình bình hành biết độ dài cạnh dài hơn độ dài cạnh ngắn 4 cm.
Hướng dẫn giải:
Nửa chu vi hình bình hành là:
48 : 2 = 24 (cm).
Độ dài cạnh dài của hình bình hành là:
(24 + 4) : 2 = 14 (cm).
Độ dài cạnh ngắn của hình bình hành là:
14 – 4 = 10 (cm).
2. Bài tập vận dụng
Bài 1. Tính chu vi và diện tích hình bình hành ABCD có các độ dài cạnh lần lượt là AB = 6 cm, BC = 8 cm và chiều cao AH = 3 cm.
Bài 2. Một hình bình hành có độ dài đáy là 24 cm, chiều cao bằng độ dài đáy. Tính diện tích của hình bình hành đó.
Bài 3. Một khu vườn dạng hình bình hành có chiều cao là 444m, độ dài đáy gấp đôi chiều cao. Tính diện tích của khu vườn đó.
Bài 4. Có một miếng đất hình bình hành cạnh đáy dài là 32,5m, chiều cao bằng cạnh đáy. Trên miếng đất người ta trồng rau, mỗi mét vuông đất thu hoạch được 2,4 kg rau. Hỏi trên miếng đất đó thu hoạch được tất cả là bao nhiêu ki-lô-gam rau ?
Bài 5.Cho hình bình hành có chu vi là 480 cm, có độ dài cạnh đáy gấp 5 lần cạnh kia. Tính chiều dài các cạnh của hình bình hành đó?
VI. Công thức tính chu vi, diện tích hình thoi
1. Lý thuyết
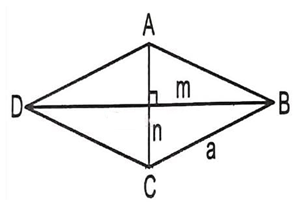
Cho hình thoi ABCD có cạnh là a và độ dài hai đường chéo lần lượt là m, n.
- Chu vi hình thoi ABCD là: C = 4 . a (đơn vị độ dài).
- Diện tích hình thoi ABCD là: S = . m . n (đơn vị diện tích).
Ví dụ 1. Cho hình thoi có cạnh là 8 cm, độ dài hai đường chéo lần lượt là 8 cm và 12 cm.
a) Tính chu vi của hình thoi?
b) Tính diện tích của hình thoi?
Hướng dẫn giải:
a) Chu vi của hình thoi là:
8 . 4 = 32 (cm).
b) Diện tích của hình thoi là:
. 8 . 12 = 48 (cm2).
Vậy chu vi hình thoi là 32cm và diện tích hình thoi là 48cm2.
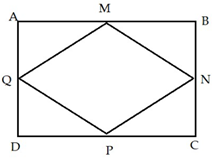
Ví dụ 2. Tính diện tích hình thoi MNPQ như hình vẽ biết các cạnh AB = 22 cm và AD = 17 cm.
Hướng dẫn giải:
Quan sát hình vẽ ta có thể thấy hình thoi có hai đường chéo là MP và NQ.
Ta thấy MP = AD = BC = 17cm
NQ = AB = CD = 22cm
Diện tích của hình thoi MNPQ là:
. 22 . 17 = 187 (cm2).
Vậy diện tích hình thoi MNPQ là 187 cm2.
Ví dụ 3. Một khu đất hình thoi có độ dài đường chéo thứ nhất là 42 m, độ dài đường chéo thứ hai bằng độ dài đường chéo thứ nhất. Người nông dân trồng khoai trên khu đất này và cứ mỗi mét vuông đất thu hoạch được 45 kg khoai. Hỏi người nông dân thu hoạch được bao nhiêu ki – lô – gam khoai?
Hướng dẫn giải:
Độ dài đường chéo thứ hai là:
42 . = 28 (m).
Diện tích của khu đất hình thoi là:
. 42 . 28 = 588 (m2).
Số ki – lô – gam khoai mà người nông dân thu được là:
588 . 45 = 26 460 (kg).
Vậy thu được 26 460 kg khoai.
2. Bài tập vận dụng
Bài 1. Cho hình thoi ABCD có cạnh bằng 10 cm, độ dài hai đường chéo lần lượt là 10 cm và 14 cm.
a) Tính chu vi của hình thoi?
b) Tính diện tích của hình thoi?
Bài 2. Một người muốn treo đèn xung quanh một khung ảnh hình thoi có cạnh là 2 m. Chi phí phải trả cho mỗi mét dài đèn là 100 000 đồng. Hỏi người này cần chi tất cả bao nhiêu tiền?
Bài 3.Người ta trồng rau trên một thửa ruộng hình thoi có tổng độ dài hai đường chéo là 50 m và đường chéo thứ nhất dài hơn đường chéo thứ hai 10 m. Trên thửa ruộng đó người ta thu hoạch được 100 kg rau. Hỏi trung bình mỗi mét vuông đất người ta thu hoạch được bao nhiêu ki-lô-gam rau?
Bài 4. Một thửa ruộng hình thoi có đường chéo lớn bằng 120 m, độ dài đường chéo bé bằng độ dài đường chéo lớn. Người ta cấy lúa trên thửa ruộng đó, cứ 1 m2 thu hoạch được 2 kg thóc. Hỏi trên thửa ruộng đó người ta thu được bao nhiêu tạ thóc?
Bài 5. Tính chu vi của hình thoi biết độ dài cạnh hình thoi là:
a) 5 m;
b) 5 dm 3cm;
c) 42 cm;
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)