Nội dung bài viết

    Xem thêm

    Tìm m để hàm số đồng biến trên khoảng

    Với tài liệu về Tìm m để hàm số đồng biến trên khoảng bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.

     

    1 17 lượt xem
    Trang trước
    Chia sẻ
    Trang sau  

    Tìm m để hàm số đồng biến trên khoảng

    I. Lý thuyết

    Chương trình phổ thông ta thường gặp dạng bài này đối với hàm số đa thức bậc 1 trên bậc 1, ta sẽ áp dụng chú ý sau:

    - Hàm số f\left( x \right)=\frac{ax+b}{cx+d},\left( ad-bc\ne 0,c\ne 0 \right) đồng biến trên từng khoảng xác định khi và chỉ khi ad-bc>0

    II. Ví dụ minh họa

    Ví dụ 1: Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y = {x^3} + mx - \frac{1}{{5{x^5}}} đồng biến trên khoảng (0; +∞)

    Giải:

    Ta có: y' = 3{x^2} + m + \frac{1}{{{x^6}}}

    Hàm số đồng biến trên khoảng (0; +∞) khi và chỉ khi

    \begin{matrix} y' = 3{x^2} + m + \dfrac{1}{{{x^6}}} \geqslant 0,\forall x \in \left( {0; + \infty } \right) \hfill \\ \Leftrightarrow 3{x^2} + \dfrac{1}{{{x^6}}} \leqslant m,\forall x \in \left( {0; + \infty } \right) \hfill \\ \end{matrix}

    Xét hàm số g\left( x \right) = 3{x^2} + \frac{1}{{{x^6}}},\forall x \in \left( {0; + \infty } \right)

    \begin{matrix} g'\left( x \right) = - 6x + \dfrac{6}{{{x^7}}} = \dfrac{{ - 6\left( {{x^8} - 1} \right)}}{{{x^7}}} \hfill \\ g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1} \\ {x = - 1\left( {ktm} \right)} \end{array}} \right. \hfill \\ \end{matrix}

    Ta có bảng biến thiên:

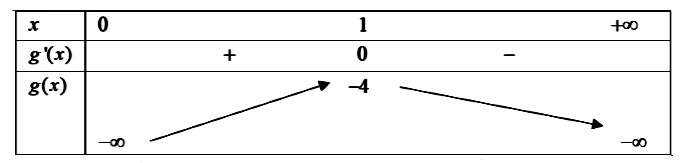
    Tìm m để hàm số đồng biến trên khoảng

    Dựa vào bảng biến thiên ta có m ≥ -4

    Suy ra các giá trị nguyên âm của tham số m thỏa mãn điều kiện đề bài là -4, -3; -2; -1

    Vậy có 4 giá trị của tham số m thỏa mãn

    Ví dụ 2: Tập hợp các giá trị của tham số m để hàm số y = x3 – 3x2+ (1 – m)x đồng biến trên khoảng (2, +∞) là:

    Giải:

    Ta có: y’ = 3x2 – 6x + 1 - m

    Hàm số y = x3 – 3x2+ (1 – m)x đồng biến trên khoảng (2, +∞) nên y’ ≥ 0 với ∀x ∈ (2, +∞)

    Suy ra: 3x2 – 6x + 1 ≥ m, ∀x ∈ (2, +∞)

    => \mathop {Min\left( {3{x^2} - 6x + 1} \right)}\limits_{x \in \left( {2; + \infty } \right)} \geqslant m \Leftrightarrow 1 \geqslant m

    Vậy m ∈ (-∞; 1] thỏa mãn điều kiện đề bài

    III. Bài tập vận dụng

    Bài 1: Tìm tất cả giá trị của m để hàm số

    y=-\frac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}+\left( m+3 \right)x-1 đồng biến trên khoảng \left( 0,3 \right).

    Giải:

    Ta có: y'=-{{x}^{2}}+2\left( m-1 \right)x+3+m

    Hàm số đồng biến trên \left( 0,3 \right)\Rightarrow y'\ge 0,\forall x\in \left( 0,3 \right)

    \Rightarrow -{{x}^{2}}+2\left( m-1 \right)x+3+m\ge 0\Leftrightarrow m\ge \frac{{{x}^{2}}+2x+3}{2x+1}

    Xét hàm số:

    f\left( x \right)=\frac{{{x}^{2}}+2x+3}{2x+1} với \forall x\in \left( 0,3 \right) \Rightarrow f\left( x \right)=\frac{{{x}^{2}}+2x+3}{2x+1},\forall x\in \left( 0,3 \right)

    Lập bảng biến thiên kết luận m\ge \frac{12}{7}

    Bài 2: Tìm m để hàm số y=\frac{\tan x-2}{\tan x-m} đồng biến trên \left( 0,\frac{\pi }{4} \right)

    Giải:

    y'=\frac{-m+2}{{{\left( \tan x-m \right)}^{2}}}\left( \tan x \right)'=\frac{-m+2}{{{\left( \tan x-m \right)}^{2}}}.\frac{1}{{{\cos }^{2}}x}

    Để hàm số đồng biến trên \left( 0,\frac{\pi }{4} \right) thì:

    y'>0,\forall x\in \left( 0,\frac{\pi }{4} \right)\Leftrightarrow \left\{ \begin{matrix} -m+2>0 \\ m\ne \tan x,x\in \left( 0,\dfrac{\pi }{4} \right) \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} m<2 \\ m\notin \left( 0,1 \right) \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{matrix} m\le 0 \\ 1\le m<2 \\ \end{matrix} \right.

    Bài 3: Tập hợp tất cả các giá trị thực của tham số m để hàm số y = \frac{{x + 3}}{{x + m}} đồng biến trên khoảng (-∞; -6)

    Giải:

    Tập xác định: D = \mathbb{R}\backslash \left\{ { - m} \right\}

    Ta có: y' = \frac{{m - 3}}{{{{\left( {x + m} \right)}^2}}}

    Để hàm số đồng biến trên khoảng (-∞; -6) ta có:

    y’ > 0 ∀x ∈ (-∞; -6)

    \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m - 3 > 0} \\ { - m \notin \left( { - \infty ; - 6} \right)} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 3} \\ { - m \geqslant - 6} \end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}} {m > 3} \\ {m \leqslant 6} \end{array} \Leftrightarrow } \right.3 < m \leqslant 6

    Vậy m ∈ (3; 6] thỏa mãn điều kiện đề bài

    Bài 4: Cho hàm số y = f\left( x \right) = \frac{{mx - 4}}{{x - m}} (m là tham số thực). Có bao nhiêu giá trị nguyên của m để hàm số đã cho đồng biến trên khoảng (0; +∞)?

    Giải

    Tập điều kiện: x ≠ m

    Ta có: y' = \frac{{ - {m^2} + 4}}{{{{\left( {x - m} \right)}^2}}}

    Để hàm số đồng biến trên khoảng (0; +∞) thì

    \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y' > 0} \\ {m \notin \left( {0; + \in } \right)} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} { - {m^2} + 4 > 0} \\ {m \leqslant 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} { - 2 < m < 2} \\ {m \leqslant 0} \end{array} \Leftrightarrow - 2 < m \leqslant 0} \right.

    Do m là số nguyên nên m = -1 hoặc m = 0

    Vậy có hai giá trị nguyên của m thỏa mãn điều kiện đề bài

    Bài 5: Tìm tất cả các giá trị thực của m để hàm số y = \frac{{\tan x - 2}}{{\tan x - m}} đồng biến trên khoảng \left( {0;\frac{\pi }{4}} \right)

    Giải

    Đặt tanx = t. Với x = 0 => t = 0 với x = \frac{\pi }{4} \Rightarrow t = 1

    Bài toán trở thành tìm m để hàm số y = \frac{{t - 2}}{{t - m}} đồng biến trên (0; 1)

    Hàm số phân thức hữu tỉ đồng biến

    y' > 0 \Leftrightarrow \frac{{2 - m}}{{{{\left( {1 - m} \right)}^2}}} > 0 \Leftrightarrow m > 2

    Ngoài ra hàm phân thức có điều kiện tồn tại x \ne m

    => m không thuộc khoảng chứa x \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m \leqslant 0} \\ {m \geqslant 1} \end{array}} \right.

    Kết hợp 2 điều kiện trên ta được \left[ {\begin{array}{*{20}{c}} {m \leqslant 0} \\ {1 \leqslant m \leqslant 2} \end{array}} \right.

    Bài 6: Tìm giá trị của tham số a để hàm số y = - \frac{1}{3}{x^3} + \left( {m - 1} \right){x^2} + \left( {m + 3} \right)x - 4 đồng biến trên khoảng (0; 3).

    Bài 7: Tìm m để hàm số y=\frac{2{{x}^{2}}-3x+m}{x-1} đồng biến trên \left( 2,+\infty \right)

    Bài 8: Tìm m để hàm số y=\sin x+mx đồng biến trên \mathbb{R}

    Bài 9: Cho hàm số y = \frac{{\left( {m - 1} \right)\sqrt {x - 1} + 2}}{{\sqrt {x - 1} - 1}}. Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (17;37).

    Bài 10: Hàm số: y = 2x3 - 3(2m + 1)x2 + 6m(m + 1)x + 1 đồng biến trên khoảng (2;+∞) khi giá trị m là?

    1 17 lượt xem
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: