100 bài toán thực tế miền nghiệm lớp 10 và cách giải (2024)

100 bài toán thực tế miền nghiệm lớp 10 và cách giải (2024)

I. Lý thuyết

1. Định nghĩa

Cặp số $(x_0;y_0)$ thỏa mãn $a{x}_0+b{y}_0\le c$ được gọi là một nghiệm của bất phương trình $ax+by\le c$.

Nghiệm của các bất phương trình $ax+by<c;ax+by>c;ax+by\ge c$ được định nghĩa tương tự.

Trong mặt phẳng tọa độ $Oxy$, miền nghiệm của bất phương trình $ax+by\le c$ là tập hợp các điểm $(x_0;y_0)$ sao cho $a{x}_0+b{y}_0\le c$.

+ Nhận xét

Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

+ Biểu diễn miền nghiệm của bất phương trình $ax+by\le c$

Bước 1: Vẽ đường thẳng $\mathrm{\Delta }:ax+by=c$

Bước 2: Lấy điểm $A(x_0;y_0)$ không thuộc $\mathrm{\Delta }$. Tính $a{x}_0+b{y}_0$ rồi so sánh với c.

Bước 3: Kết luận

Nếu $a{x}_0+b{y}_0<c$ thì miền nghiệm là nửa mặt phẳng (kể cả bờ $\mathrm{\Delta }$) chứa điểm $A(x_0;y_0)$.

Nếu $a{x}_0+b{y}_0>c$ thì miền nghiệm là nửa mặt phẳng (kể cả bờ $\mathrm{\Delta }$) không chứa điểm $A(x_0;y_0)$.

Chú ý: Đường thẳng $\mathrm{\Delta }:ax+by=c$ là tập hợp các điểm (x;y) thỏa mãn $ax+by=c$.

Do đó miền nghiệm của các bất phương trình $ax+by<c;ax+by>c$ không chứa đường thẳng $\mathrm{\Delta }$ (hay không kể bờ $\mathrm{\Delta }$), khi đó ta thường vẽ $\mathrm{\Delta }$ bằng nét đứt.

2. Ví dụ minh họa

+ Nghiệm của bất phương trình bậc nhất hai ẩn:

Cặp số $(2;-1)$ là một nghiệm của bất phương trình $3x+2y\ge -5$, vì $3.2+2.(-1)=4\ge -5$

Cặp số $(-2;0)$ không là một nghiệm của bất phương trình $3x+2y\ge -5$, vì $3.(-2)+2.0=-6<-5$

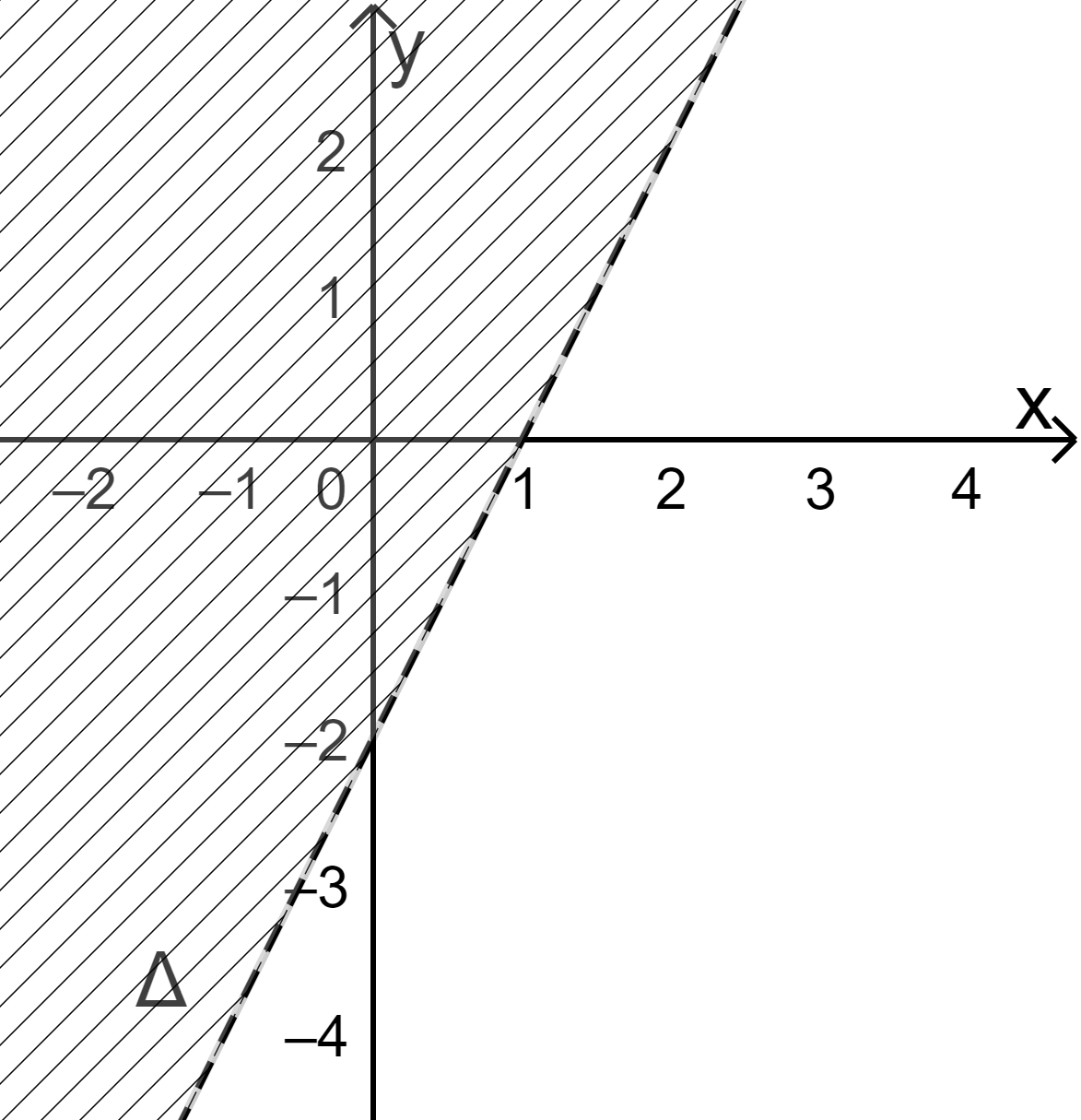
+ Biểu diễn miền nghiệm của bất phương trình $2x-y>2$

Bước 1: Vẽ đường thẳng $\mathrm{\Delta }:2x-y=2$ (nét đứt) đi qua (1;0) và (0; -2).

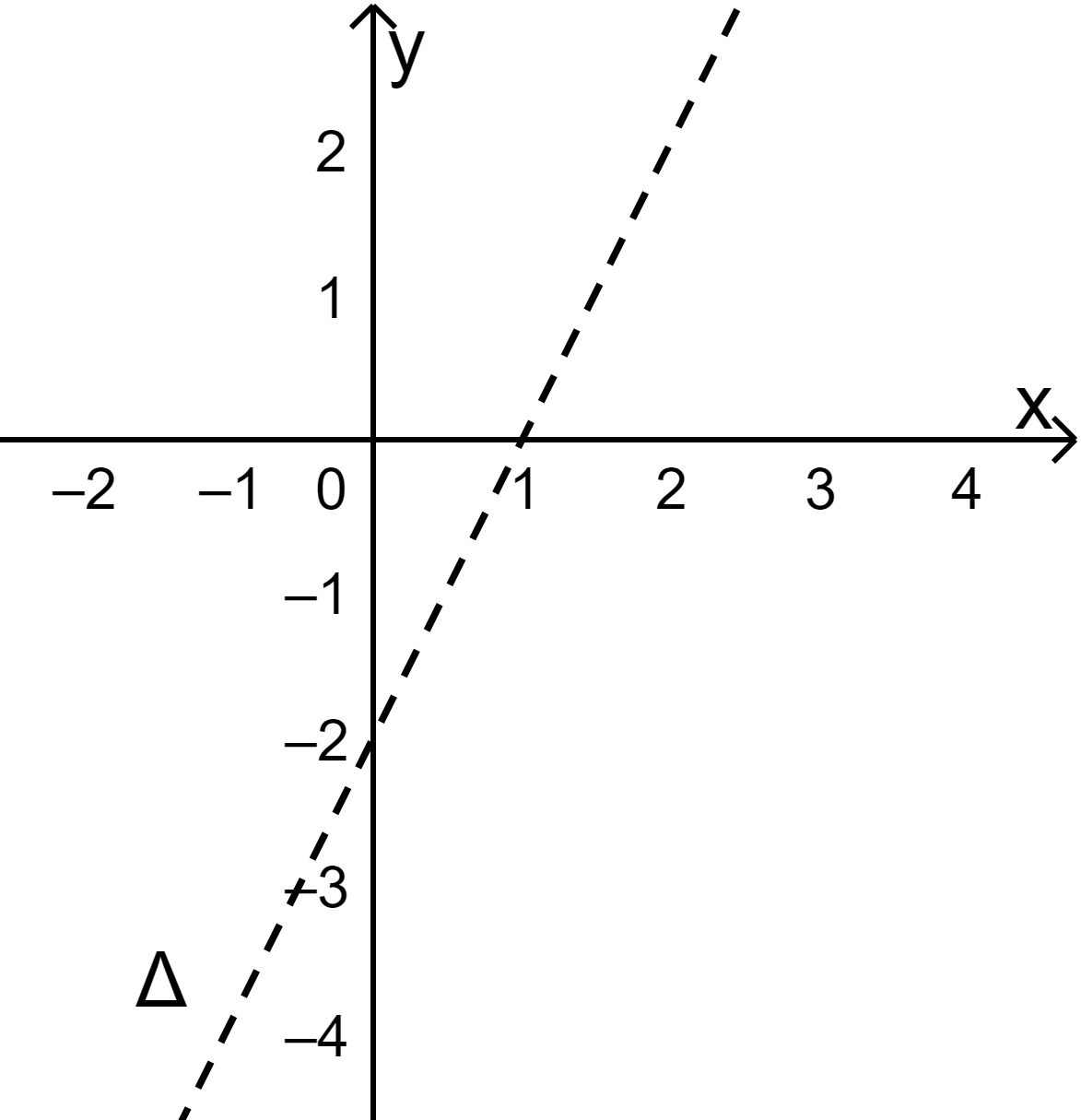
Bước 2: Lấy điểm $O(0;0)$ không thuộc $\mathrm{\Delta }$. Ta có $2.0-0=0$ và $c=2$.

Bước 3: Vì $2.0-0=0<2$ nên điểm $O(0;0)$ không thuộc miền nghiệm.

Vậy miền nghiệm là nửa mặt phẳng (không kể bờ $\mathrm{\Delta }$) không chứa điểm $O(0;0)$ (miền không gạch chéo).

II. Bài tập vận dụng

Bài 1. Hàng tuần bạn HS dành tối đa 14 giờ đồng hồ để tập thể dục giữ vóc dáng, bạn tập cả hai môn là đạp xe và boxing. Biết rằng mỗi giờ đạp xe tiêu hao 600 calo và mỗi giờ tập boxing tiêu hao 900 calo. Bạn HS muốn tiêu hao nhiều calo nhưng không vượt quá 10800 calo cho tập cả hai môn này mỗi tuần. Hỏi số giờ dành cho tập cả hai môn đạp xe và boxing trong mỗi tuần là bao nhiêu để số calo tiêu hao nhiều nhất?

Lời giải

Gọi $x,y$ là . . . , có hệ $\{\begin{array}{rl}& x+y\le 14\\ & 600x+900y\le 10800\\ & x\ge 0\\ & y\ge 0\end{array}$ $\iff \{\begin{array}{rl}& x+y\le 14\\ & 2x+3y\le 36\\ & x\ge 0\\ & y\ge 0\end{array}$. KL: 6 giờ đạp xe, 8 giờ boxing.

Bài 2. Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

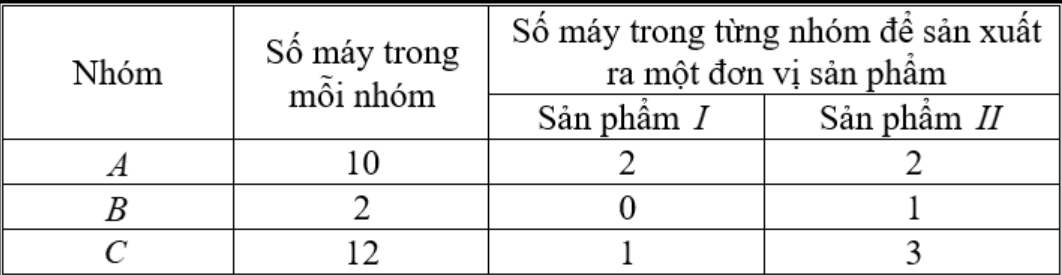
Cho biết một đơn vị sản phẩm I lãi 30 nghìn đồng, một đơn vị sản phẩm II lãi 50 nghìn đồng.

Em hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.

Lời giải:

Gọi $x$ và $y$ lần lượt là số đơn vị sản phẩm $I$ và $II$ $(x,y\ge 0)$.

Số tiền lãi là $30x+50y$ (nghìn đồng). Ta có hệ bất phương trình:

$\{\begin{array}{l}2x+2y\le 10\\ y\le 2\\ x+3y\le 12\\ x,y\ge 0\end{array}$

Giải ra sản xuất 3 sản phẩm I và 2 sản phẩm .

Bài 3. Một đoàn thám hiểm vùng cực hiện cách căn cứ 240km. Trong vòng 48 giờ tới sẽ có một cơn bão tuyết ập đến. Đoàn phải di chuyển càng nhiều càng tốt bằng tàu rồi đi bộ về căn cứ đoạn đường còn lại trước khi con bão đến. Đoàn thám hiếm có thể điều khiển tàu phá băng với vận tốc 12km/h hoặc đi bộ với vận tốc 3km/h. Viết và vẽ hệ bất phương trình xác định khoảng thời gian đoàn thám hiểm có thế đi bằng tàu phá băng rồi đi bộ để trở về căn cứ trước khi con bão đến.

_{Lời giải}

_{Gọi thời gian đoàn thám hiểm điều khiển tàu phá băng là x giờ, thời gian đoàn thám hiểm đi bộ là y giờ. Ta có .}

$\{\begin{array}{rl}& x\ge 0\\ & y\ge 0\\ & x+y\le 48\\ & 12x+3y\ge 240\end{array}$

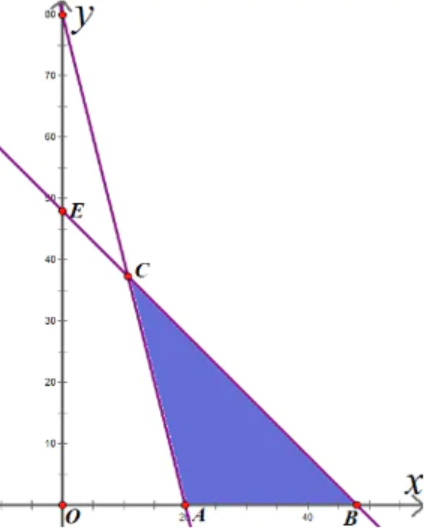
Bài 4. Bác An định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8ha (hecta). Nếu trồng 1ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác An cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác An chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.

Lời giải

Gọi x là số hecta đất trồng ngô và y là số hecta đất trồng đậu xanh.

Có $\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 8\\ 2x+3y\le 18\end{array}$. Tiền lãi $F(x;y)=40x+50y$.

Biểu diễn miền nghiệm của hệ trên hệ toạ độ Oxy , và có kết quả cần trồng 6ha ngô và 2ha đậu xanh.

Bài 5. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipid. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipid. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6 kilôgam thịt bò và 1,1 kilôgam thịt lợn; giá tiền 1 kilôgam thịt bò là 250 nghìn đồng; 1 kilôgam thịt lợn là 160 nghìn đồng. Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải

Mua 0,3 kilôgam thịt bò và 1,1 kilôgam thịt lợn

Bài 6. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là bao nhiêu?

Lời giải

Gọi x,y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x,y nguyên dương.

Ta có hệ bất phương trình sau: $\{\begin{array}{l}3x+2y\le 180\\ x+6y\le 220\\ x>0\\ y>0\end{array}$

Miền nghiệm của hệ trên là

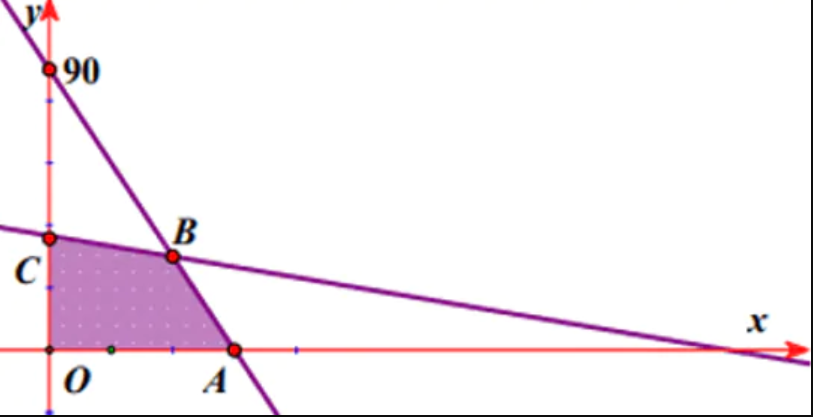
Tiền lãi trong một tháng của xưởng là T=0,5x+0,4y (triệu đồng).

Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A,B,C. Vì C có tọa độ không nguyên nên loại.

Tại A(60;0) thì T=30 triệu đồng.

Tại B(40;30) thì T=32 triệu đồng.

Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

Bài 7. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 gam hương liệu, 9 lít nước và 210 gam đường để pha chế nước ngọt loại I và nước ngọt loại II. Để pha chế 1 lít nước ngọt loại I cần 10 gam đường, 1 lít nước và 4 gam hương liệu. Để pha chế 1 lít nước ngọt loại II cần 30 gam đường, 1 lít nước và 1 gam hương liệu. Mỗi lít nước ngọt loại I được 80 điểm thưởng, mỗi lít nước ngọt loại II được 60 điểm thưởng. Hỏi số điểm thưởng cao nhất có thể của mỗi đội trong cuộc thi là bao nhiêu?

Lời giải

Gọi số lít nước ngọt loại $I$ là $x$ và số lít nước ngọt loại II là $y$. Khi đó ta có hệ điều kiện về vật liệu ban đầu mà mỗi đội được cung cấp: $\{\begin{array}{c}10x+30y\le 210\\ 4x+y\le 24\\ x+y\le 9\\ x,y\ge 0\end{array}\iff \{\begin{array}{c}x+3y\le 210\\ 4x+y\le 24\\ x+y\le 9\\ x,y\ge 0\end{array}$

Điểm thưởng đạt được: $P=80x+60y$

Bài toán đưa về tìm giá trị lớn nhất của biểu thức $P$ trong miền $D$ được cho bởi hệ điều kiện (*) Biến đổi biểu thức $P=80x+60y\iff 80x+60y-P=0$ đây là họ đường thẳng ${\mathrm{\Delta }}_{(P)}$ trong hệ tọa độ $Oxy$

Miền $D$ được xác định trong hình vẽ bên dưới

Bài 8. Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (1 sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng.

Lời giải

Gọi $x$ là số xe loại $A(0\le x\le 10;x\in \mathbb{N}),y$ là số xe loại $B(0\le y\le 9;y\in \mathbb{N})$. Khi đó tổng chi phí thuê xe là $T=4x+3y$ (triệu đồng).

Xe $A$ chở tối đa 20 người, xe $B$ chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là $20x+10y$ (người).

Xe $A$ chở được 0,6 tấn hàng, xe $B$ chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là $0,6x+1,5y$ (tấn).

Theo giả thiết, ta có $\{\begin{array}{l}0\le x\le 10\\ 0\le y\le 9\\ 20x+10y\ge 140\\ 0,6x+1,5y\ge 9\end{array}(\ast )$

Biểu diễn miền nghiệm của hệ bất phương trình $(\ast )$ là tứ giác $ABCD$ kể cả miền trong của tứ giác (như hình vẽ trên).

Biểu thức $T=4x+3y$ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác $ABCD$.

Tại các đỉnh $A(10;2);B(10;9);C\left(\frac{5}{2};9\right);D(5;4)$, ta thấy $T$ đạt giá trị nhỏ nhất tại $\{\begin{array}{l}x=5\\ y=4\end{array}$.

Khi đó $T_{min}=32$ (triệu đồng).

Bài 9. Một hộ nông dân định trồng đậu và cà trên diện tích . Nếu trồng đậu trên diện tích 100m2 thì cần 20 công làm và thu được 3000000 đồng. Nếu trồng cà trên diện tích 100m2 thì cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công.

Lời giải

Giả sử diện tích trồng đậu là $x$ (trăm $m^2$); suy ra diện tích trồng cà là $8-x$ (trăm $m^2$ )

Ta có thu nhập thu được là $S(x)=[3x+4(8-x)]\cdot 10000=10000(-x+32)$ đồng.

Tổng số công là $20x+30(8-x)=-10x+240$

Theo giả thiết có $-10x+240\le 180\iff x\ge 6$

Mà hàm số $S(x)$ là hàm nghịch biến trên $\mathbb{R}$ nên $S(x)$ đạt giá trị lớn nhất khi $x=6$.

Do đó trồng $600m^2$ đậu, $200m^2$ cà.

Bài 10. Ông An muốn thuê một chiếc xe ô-tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

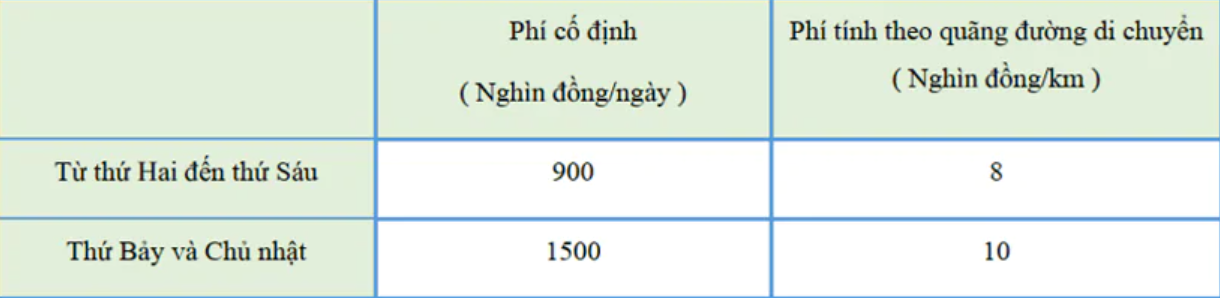
a) Gọi x và y lần lượt là số kilômet ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.

b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.

Lời giải

a) Từ thứ Hai đến thứ Sáu. $1km$ di chuyển có chi phí là 8000 ( đồng ). Ông An đi hết $x(km)$, vậy ông An sẽ tốn chi phí là: $8000x$ ( đồng ).

Tương tự vào hai ngày cuối tuần, Ông An đi hết $y(km)$, vậy ông An sẽ tốn chi phí là: $10000y$( đồng ).

Vậy tổng số tiền ông An phải chi là: $8000x+10000y$.

Theo bài ra ta có: $8000x+10000y\le 14.000.000\iff 4x+5y\le 7000$.

b) Biểu diễn miền nghiệm của BPT ở câu a) trên mặt phẳng tọa độ

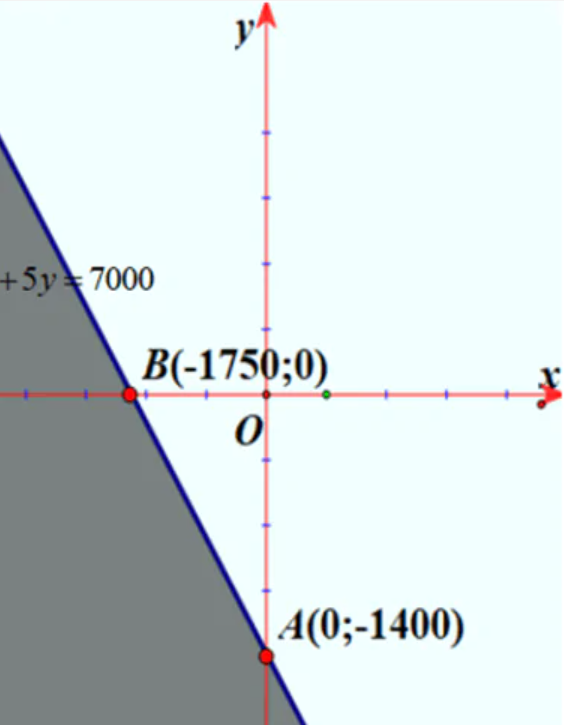
Bài 11. Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg ạo nếp, 2kg thịt ba chỉ, 5kg đậu xanh để gói bánh chưng và bánh ống. Để gói một cái bánh chưng cần 0,4kg gạo nếp, 0,05kg thịt và 0,1kg đậu xanh; để gói một cái bánh ống cần 0,6kg gạo nếp, 0,075kg thịt và 0,15kg đậu xanh. Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh ống nhận được 7 điểm thưởng. Hỏi cần phải gói mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất?

Lời giải

Gọi số bánh chưng gói được là $x$, số bánh ống gói được là $y$. Khi đó số điểm thưởng là $f(x;y)=$ $5x+7y$

Số $kg$ gạo nếp cần dùng là $0,4x+0,6y$.

Số kg thịt ba chỉ cần dìng là $0,05x+0,075y$.

Số kg đậu xanh cần dùng là $0,1x+0,15y$.

Vì trong cuộc thi này chỉ được sử dụng tối đa $20kg$ gạo nếp, $2kg$ thịt ba chỉ và $5kg$ đậu xanh nên ta có hệ bất phương trình

$\{\begin{array}{l}0,4x+0,6y\le 201\\ 0,05x+0,075y\le 2\\ 0,1x+0,15y\le 5\\ 0,1x+0,15y\le 5\\ x,y\ge 0\end{array}$ $\iff \{\begin{array}{l}2x+3y\le 100\\ 2x+3y\le 80\\ 2x+3y\le 100\\ x,y\ge 0\end{array}$ $\iff \{\begin{array}{l}2x+3y\le 80\\ x,y\ge 0\end{array}(\ast )$

Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x;y)$ trên miền nghiệm của hệ bất phương trình (*).

Miền nghiệm của hệ bất phương trình (*) là tam giác $OAB$ (kể cả biên).

Hàm số $f(x;y)=5x+5y$ sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi $(x;y)$ là toạ độ một trong các đỉnh $O(0;0),A(40;0),B\left(0;\frac{80}{3}\right)$.

Ta có: $f(0;0)=0,f(40;0)=200,f\left(0;\frac{80}{3}\right)=\frac{560}{3}$.

Suy ra $f(x;y)$ lớn nhất khi $(x;y)=(40;0)$. Do đó cần phải gói 40 cái bánh chưng để nhận được số điểm thưởng là lớn nhất.

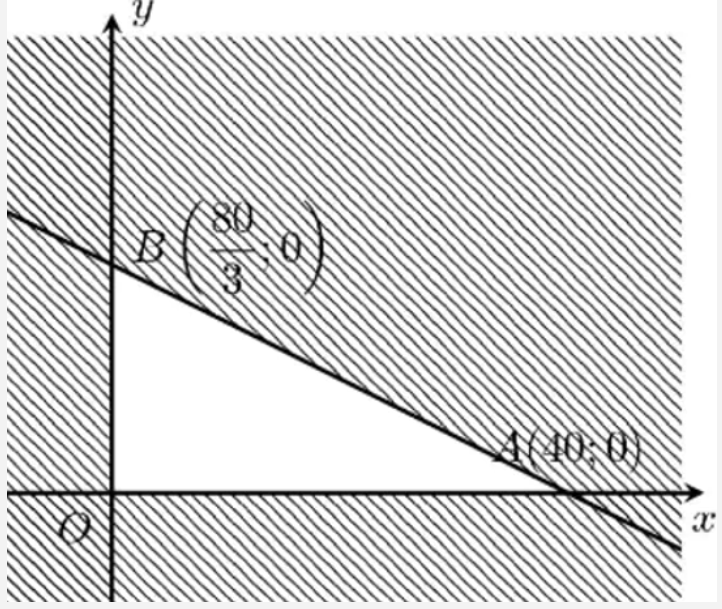
Bài 12. Một máy cán thép có thể sản xuất hai sản phẩm thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 25 USD, mỗi tấn thép cuộn có giá 30 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất.

Lời giải

Gọi $x$ và $y$ lần lượt là số tấn thép tấm và số tấn thép cuộn mà máy cán thép này sản xuất trong một tuần $(x;y\ge 0)$.

Số tiền lãi thu được là: $f(x;y)=25x+30y$ (USD).

Thời gian để sản xuất $x$ tấn thép tấm là: $\frac{x}{250}$ (giờ).

Thời gian để sản xuất $y$ tấn thép cuộn là: $\frac{y}{150}$ (giờ).

Ta có hệ bất phương trình sau: $\{\begin{array}{l}0\le x\le 5000\\ \frac{x}{250}+\frac{y}{150}\le 40\\ 0\le y\le 3500\end{array}$ $\iff \{\begin{array}{l}0\le x\le 5000\\ 0\le y\le 3500\\ 3x+5y\le 30000\end{array}$ (*)

Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x;y)$ trên miền nghiệm của hệ bất phương trình (*). Miền nghiệm của hệ (*) là ngũ giác ABCD (kể cả biên), trong đó $A(5000;0), B(5000;3000)$, $C\left(\frac{12500}{3};3500\right),D(0;3500)$.

Suy ra $f(x;y)$ đạt giá trị lớn nhất trên miền nghiệm của hệ $(\ast )$ khi $(x;y)=(5000;3000)$.

Như vậy cần phải sản xuất 5000 tấn thép tấm và 3000 tấn thép cuộn trong một tuần để lợi nhuận thu được lớn nhất.

Bài 13. Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thế làm 40 giờ/tuần và tốn 6 giờ để làm một cái bàn, 3 giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế it nhất là gấp ba lần số bàn. Một cái bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Hỏi người thợ mộc phải sản xuất như thế nào để số tiền lãi thu về là lớn nhất.

Lời giải

Gọi $x$ và $y$ lần lượt là số bàn và số ghế mà người thợ mộc sản xuất trong một tuần $(x,y\ge 0)$. Khi đó số tiền mà người thợ mộc thu được là: $f(x;y)=150x+50y$ (nghìn đồng).

Ta có hệ bất phương trình sau: $\{\begin{array}{l}6x+3y\le 40\\ y\ge 3x\\ x+\frac{y}{4}\le 4\\ x,y\ge 0\end{array}$ $\iff \{\begin{array}{l}6x+3y\le 40\\ y\ge 3x\\ 4x+y\le 16\\ x,y\ge 0\end{array}$

Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x;y)=150x+50y$ trên miền nghiệm của hệ (*).

Miền nghiệm của hệ (*) là tứ giác $OABC$ (kể cả biên).

Ta có toạ độ điểm $A$ là nghiệm của hệ phương trình: $\{\begin{array}{l}y=3x\\ 4x+y=16\end{array}$ $\Rightarrow A\left(\frac{16}{7};\frac{48}{7}\right).$

Toạ độ điểm $B$ là nghiệm của hệ phương trình: $\{\begin{array}{l}6x+3y=40\\ 4x+y=16\end{array}$ $\Rightarrow B\left(\frac{4}{3};\frac{32}{3}\right).$

Toạ độ điểm $C$ là nghiệm của hệ phương trình: $\{\begin{array}{l}x=0\\ 6x+3y=40\end{array}$ $\Rightarrow C\left(0;\frac{40}{3}\right).$

Ta thấy $f(x;y)$ lớn nhất khi $(x;y)=\left(\frac{4}{3};\frac{32}{3}\right)$.

Như vậy người thợ này cần sản xuất 4 cái bàn và 32 cái ghế trong vòng 3 tuần để thu về số tiền lãi lớn nhất.

Bài 14. Cho hệ bất phương trình $\{\begin{array}{l}x-2y\le 0\\ x+3y\ge -2.\\ x\le 0\end{array}$ Tìm giá trị lớn nhất của hàm số $f(x;y)=2x-3y$ trên miền nghiệm của hệ bất phương trình đã cho..

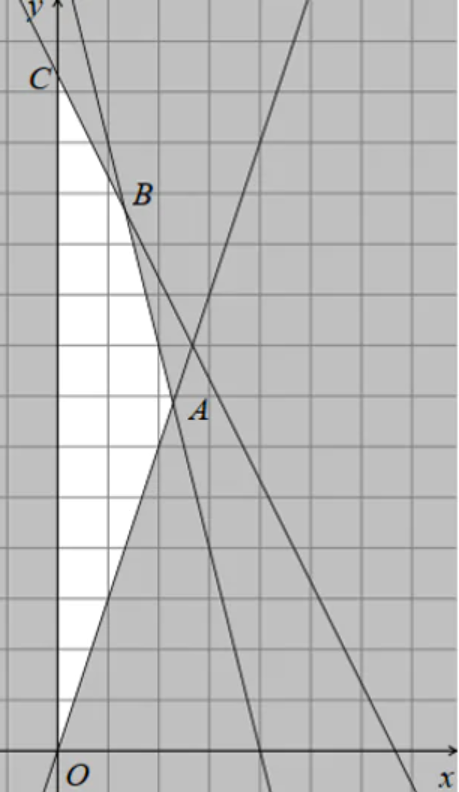
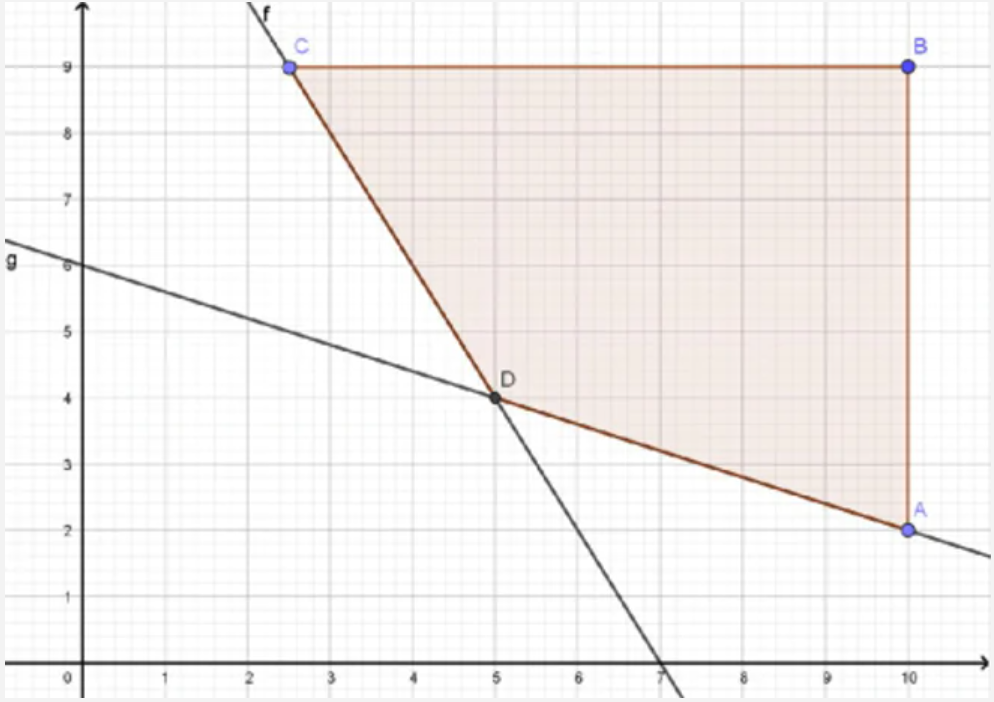
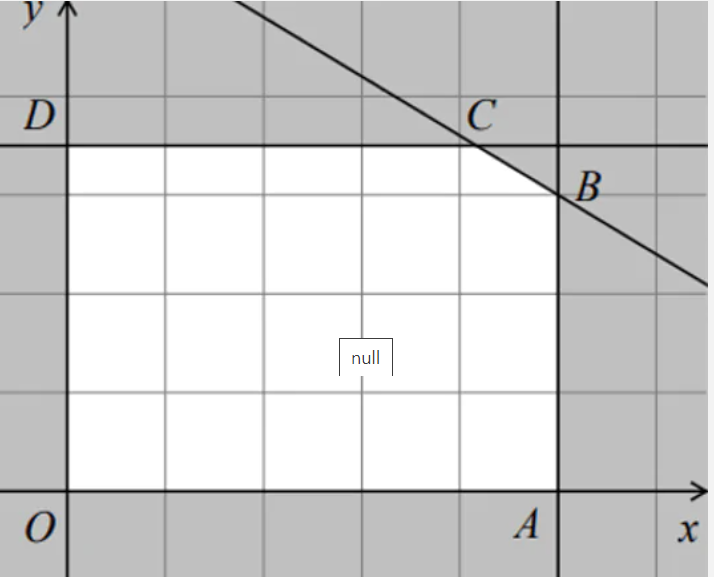
Lời giải

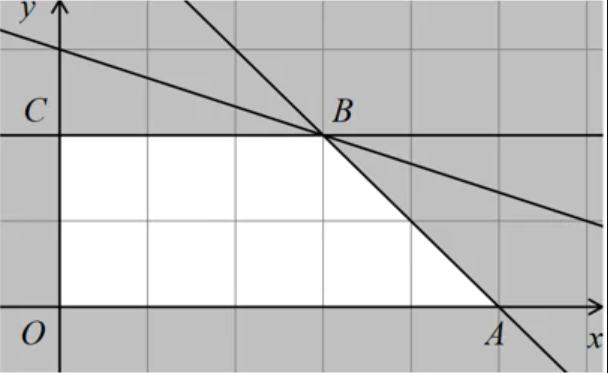
Chúng ta tìm được miền nghiệm của hệ bất phương trình đã cho là phần không tô đậm trong hình vẽ bên (kể cả biên).

Như vậy miền nghiệm là tam giác ABC (kể cả biên).

Toạ độ của điểm $A$ là nhiệm của hệ phương trình: $\{\begin{array}{l}x-2y=0\\ x+3y=-2\end{array}$ $\Rightarrow A\left(-\frac{4}{5};-\frac{2}{5}\right).$

Toạ độ của điểm $B$ là nghiệm của hệ phương trình: $\{\begin{array}{l}x+3y=-2\\ x=0\end{array}$ $\Rightarrow B\left(0;\frac{-2}{3}\right).$

Ta sẽ tính các giá trị của $f(x;y)$ với $(x;y)$ là toạ độ của các đỉnh $A,B,O$.

$f\left(-\frac{4}{5};-\frac{2}{5}\right)=2\cdot \left(-\frac{4}{5}\right)-3\cdot \left(-\frac{2}{5}\right)=-\frac{2}{5}.f(0;0)=2\cdot 0-3\cdot 0=0.f\left(0;-\frac{2}{3}\right)=2\cdot 0-3\cdot \left(-\frac{2}{3}\right)=2.$

Suy ra giá trị lớn nhất của $f(x;y)$ bằng 2 khi $(x;y)=\left(0;-\frac{2}{3}\right)$.

Vậy giá trị lớn nhất của hàm số $f(x,y)=2x-3y$ trên miền nghiệm của hệ bất phương trình đã cho bằng 2 khi $(x;y)=\left(0;-\frac{2}{3}\right)$

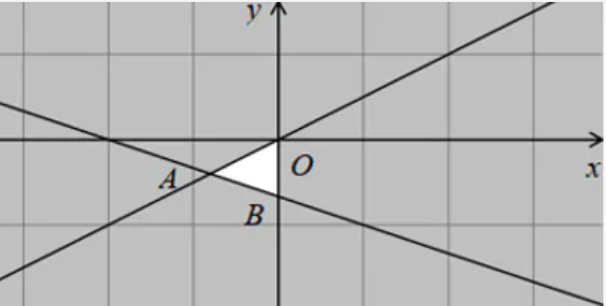
Bài 15. Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và một máy chuyên dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg nguyên liệu và máy làm việc trong 3 giờ. Để sản xuất được một kilôgam sản phẩm loại II cần 4kg nguyên liệu và máy làm việc trong 1,5 giờ. Biết một kilôgam sản phẩm loại I lãi 300000 đồng, một kilôgam sản phẩm loại II lãi 400000 đồng và máy chuyên dụng làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao nhiêu kilôgam sản phẩm mỗi loại để tiền lãi lớn nhất.

Lời giải

Giả sử sản xuất $x(kg)$ sản phẩm loại I và $y(kg)$ sản phẩm loại II.

Điều kiện $x\ge 0,y\ge 0$và $2x+4y\le 200\iff x+2y\le 100$

Tổng số giờ máy làm việc: $3x+1,5y$

Ta có $3x+1,5y\le 120$

Số tiền lãi thu được là $T=300000x+400000y$ (đồng).

Ta cần tìm $x,y$ thoả mãn: $\{\begin{array}{rl}& x\ge 0,y\ge 0\\ & x+2y\le 100\\ & 3x+1,5y\le 120\end{array}$ (I) sao cho $T=300000x+400000y$ đạt giá trị lớn nhất.

Trên mặt phẳng tọa độ $Oxy$ vẽ các đường thẳng $d_1:x+2y=100;d_2:3x+1,5y=120$

Đường thẳng $d_1$ cắt trục hoành tại điểm $A(100;0)$, cắt trục tung tại điểm $B(0;50)$.

Đường thẳng $d_2$ cắt trục hoành tại điểm $C(40;0)$, cắt trục tung tại điểm $D\left(0;80\right)$.

Đường thẳng $d_1$ và $d_2$ cắt nhau tại điểm $E\left(20;40\right)$.

Biểu diễn hình học tập nghiệm của hệ bất phương trình (I) là miền đa giác $OBEC$.

$\{\begin{array}{rl}& x=0\\ & y=0\end{array}\Rightarrow T=0$;

$\{\begin{array}{rl}& x=0\\ & y=50\end{array}\Rightarrow T=20000000$;

$\{\begin{array}{rl}& x=20\\ & y=40\end{array}\Rightarrow T=22000000$;

$\{\begin{array}{rl}& x=40\\ & y=0\end{array}\Rightarrow T=12000000$

Vậy để thu được tổng số tiền lãi nhiều nhất thì xưởng cần sản xuất $20kg$ sản phẩm loại I và $40kg$ sản phẩm loại II.

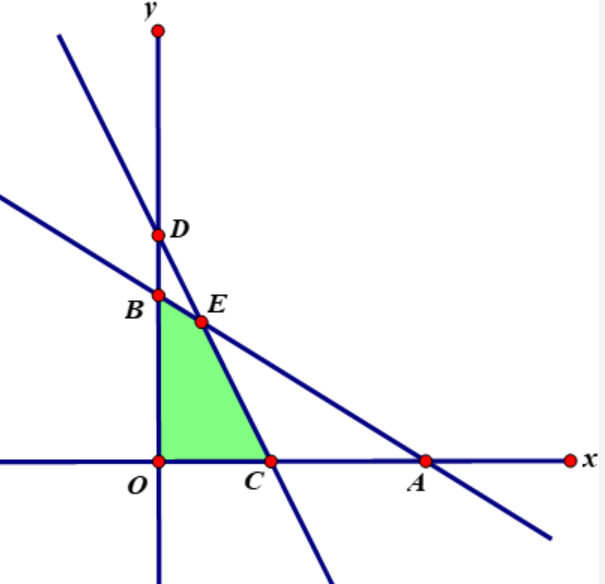
Bài 16. Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể người. Theo đó một người mỗi ngày có thể tiếp nhận được không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B; một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B. Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn 1/2 số đơn vị vitamin A nhưng không nhiều hơn 3 lần số đơn vị vitamin A. Giá của một đơn vị vitamin A là 9 đồng, giá của một đơn vị vitamin B là 7,5 đồng. Hỏi cần chi ít nhất bao nhiêu tiền mỗi ngày để dùng đủ cả hai loại vitamin trên.

Lời giải

Gọi $x$ và $y$ lần lượt là số đơn vị vitamin $A$ và $B$ dùng mỗi ngày $(x;y\ge 0)$. Số tiền cần chi là $f(x;y)=9x+7,5y$ đồng.

Ta có hệ bất phương trình:

(*)

Bài toán trở thành tìm giá trị lớn nhất của hàm số $f(x;y)$ trên miền nghiệm của hệ (*).

Miền nghiệm của hệ (*) là ngũ giác $ABCDEF$ (kể cả biên) với $A(100;300)$, $B\left(\frac{800}{3};\frac{400}{3}\right),C(600;300),D(600;400)$, $E(500;500),F\left(\frac{500}{3};500\right)$.

Suy ra $maxf(x;y)=f(100;300)=3150$.

Tức là cần chi 3150 đồng hàng ngày để sử dụng vitamin.

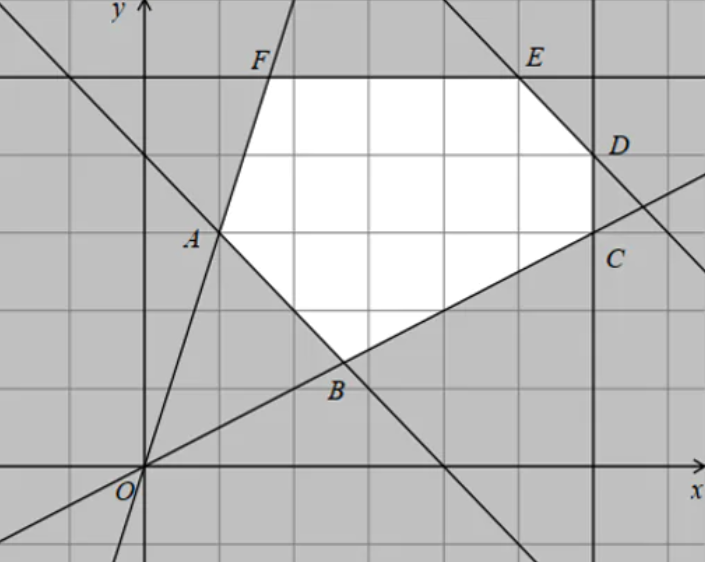
Bài 17. Giá cước đi taxi của một công ty được cho như bảng sau

a. Bạn An đi taxi để về quê với quãng đường 36km, hỏi bạn phải trả bao nhiêu tiền đi taxi?

b. Lập công thức biểu diễn số tiền phải trả theo quãng đường khi đi taxi.

a. $20000+17600\left(26-0,9\right)+14400\left(33-26\right)+11000\left(36-33\right)=595560$(đ).

b. Gọi $x,y$ là . . . , có

Bài 18. Trong toán học và nghệ thuật, hai đại lượng được gọi là có tỷ số vàng hay tỷ lệ vàng nếu tỷ số giữa tổng của các đại lượng đó với đại lượng lớn hơn bằng tỷ số giữa đại lượng lớn hơn với đại lượng nhỏ hơn. Tỷ lệ vàng thường được ký hiệu bằng ký tự (phi) trong bảng chữ cái Hy Lạp nhằm tưởng nhớ đến Phidias, nhà điêu khắc đã xây dựng nên đền Parthenon. Tỷ lệ vàng được biểu diễn trong đó Hình chữ nhật tỷ lệ vàng với cạnh dài $a$ và cạnh ngắn $b$, khi đặt cạnh hình vuông có cạnh $a$, sẽ tạo thành hình chữ nhật đồng dạng tỷ lệ vàng với cạnh dài $a+b$ và cạnh ngắn $a$. Đây cũng minh họa cho liên hệ $\frac{a+b}{a}=\frac{a}{b}=\phi$.

Bằng kiến thức liên quan đến toán học, em hãy nêu một lí do mà Hiến pháp năm 2013 đã quy định: Quốc kỳ nước Cộng hoà xã hội chủ nghĩa Việt Nam hình chữ nhật có chiều rộng bằng hai phần ba chiều dài.

Hướng dẫn câu 19:

Từ $\frac{a+b}{a}=\frac{a}{b}=\phi$ giải ra $\phi =\frac{1+\sqrt{5}}{2}$. Lại có $\frac{1+\sqrt{5}}{2}\approx \frac{3}{2}$ . . .

Bài 19. Nhịp tim là một chỉ số sức khỏe quan trọng mà tất cả chúng ta cần quan tâm, chỉ số này được đo bằng số lần co bóp của tim trong mỗi phút, nhịp tim được kí hiệu là bpm (beat per minute). Đối với hầu hết người trưởng thành khỏe mạnh, nhịp tim nghỉ ngơi dao động từ 60 bpm đến 100 bpm. Nếu bạn hoạt động thể chất thường xuyên thì nhịp tim khi nghỉ ngơi có thể thấp dưới 60 bpm, thậm chí ở các vận động viên con số này chỉ là 40 bpm. Nhịp tim tối đa là nhịp đập khi tim làm việc hết sức để đáp ứng nhu cầu oxy của cơ thể. Để có một trái tim khỏe mạnh chúng ta cần thường xuyên tập thể dục đúng theo tiêu chuẩn và cường độ phù hợp với mỗi người.

Các nhà khoa học đã đưa ra công thức khuyến cáo giữa nhịp tim tối đa và độ tuổi là: MHR = 220 – tuổi.

Nghiên cứu gần đây công thức giữa nhịp tim tối đa và độ tuổi được sửa đổi là: MHR = 208 – (0,7 x tuổi).

Người ta chỉ ra rằng nhịp tim tối đa ở độ tuổi cả công thức mới và công thức cũ cho chính xác cùng một giá trị, thì tập thể dục hiệu quả nhất khi nhịp tim đạt đến 75% của nhịp tim tối đa. Hỏi đó là năm bao nhiêu tuổi và nhịp tim tối đa lúc này là bao nhiêu ?

Lời giải

220 – tuổi = 208 – (0,7 x tuổi) ra kết quả tuổi bằng 40. Nhịp tim tối đa là 75% x 180 = 135 (bpm).

Bài 20. Cho biết quỹ đạo chuyển động của một quả bóng khi được đá lên là một cung parabol trong mặt phẳng với toạ độ là (t;h) trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên, h là độ cao (tính bằng ) của quả bóng. Một cầu thủ đá bóng từ độ cao 1.2m sau đó 1 giây, nó đạt độ cao 8.5m và sau 2 giây khi đá lên, nó đạt độ cao 6m.

a. Hãy tìm hàm số bậc hai mô tả quỹ đạo chuyển động của quả bóng ?

b. Tính chính xác đến hàng phần nghìn độ cao lớn nhất của quả bóng ?

c. Sau bao lâu thì quả bóng chạm đất kể từ khi đá lên (tính chính xác đến hàng phần trăm)?

Lời giải

a. Gọi hàm số bậc hai cần tìm là $y=a{t}^2+bt+c(a\ne 0)$. Theo giả thiết ta có hệ phương trình

$\{\begin{array}{l}y(0)=c=1,2\\ y(1)=a+b+c=8,5\\ y(2)=4a+2b+c=6\end{array}$ $\iff \{\begin{array}{l}a=-4,9\\ b=12,2\\ c=1,2\end{array}$ $\Rightarrow y=-4,9x^2+12,2x+1,2$.

b. Đáp số 8,794m.

c. Cách 1: thay giá trị $t$ trực tiếp của từng phương án vào hàm số để rút ra kết luận.

Cách 2: giải phương trình $-4,9t^2+12,2t+1,2=0\iff [\begin{array}{l}t=-0,09\\ t=2,58\end{array}$.