Nội dung bài viết

    Xem thêm

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập

    Với tài liệu về Khoảng cách giữa 2 đường thẳng chéo nhau bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.

    1 179 05/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Khoảng cách giữa 2 đường thẳng chéo nhau

    1. Định nghĩa khoảng cách giữa 2 đường thẳng chéo nhau

    Trong không gian tọa đọ Oxyz, có 4 vị trí tương đối của 2 đường thẳng đó là trùng nhau, cắt nhau, chéo nhau và song song. Trong trường hợp 2 đường thẳng chéo nhau, khoảng cách giữa chúng là độ dài đoạn vuông góc chung của 2 đường thẳng. Trong đó, đoạn thẳng nối 2 điểm trên 2 đường thẳng chéo nhau, đồng thời vuông góc với cả 2 đường thẳng đó chính là đoạn vuông góc chung.

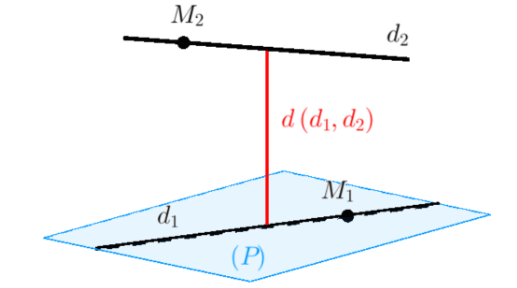
    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Lưu ý, đoạn vuông góc chung của 2 đường thẳng chéo nhau là chỉ có một và tồn tại duy nhất.

    2. Phương pháp tính khoảng cách giữa 2 đường thẳng chéo nhau

    Để có thể tính được khoảng cách giữa 2 đường thẳng chéo nhau thì chúng ta có thể sử dụng một trong các cách dưới đây:

    Phương pháp 1: Dựng đoạn vuông góc chung MN của a và b, khi đó d (a,b) = MN.

    Tuy nhiên, khi dựng đoạn vuông góc chung MN, chúng ta có thể sẽ gặp phải các trường hợp sau:

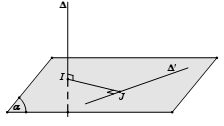
    - Trường hợp 1: ∆ và ∆’ vừa chéo vừa vuông góc với nhau

    Khi gặp trường hợp này, chúng ta sẽ làm như sau:

    • Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
    • Bước 2: Trong mặt phẳng (α) kẻ đường thẳng IJ vuông góc với ∆’

    Khi đó IJ chính là đoạn vuông góc chung và d (∆, ∆’) = IJ.

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    - Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau

    • Bước 1: Bạn chọn một mặt phẳng (α) chứa ∆’ và song song với ∆
    • Bước 2: Bạn dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M thuộc ∆ dựng đoạn MN vuông góc với (α) . Khi đó, d  sẽ là đường thẳng đi qua N và song song với ∆
    • Bước 3: Bạn gọi H là giao điểm của đường thẳng d với ∆’, dựng HK // MN

    Khi đó, HK chính là đoạn vuông góc chung và d (∆, ∆’) = HK = MN.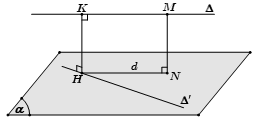Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Hoặc bạn làm như sau:

    • Bước 1: Chọn mặt phẳng (α) vuông góc với ∆ tại I
    • Bước 2: Bạn tìm hình chiếu d của ∆’ xuống mặt phẳng (α)
    • Bước 3: Trong mặt phẳng (α), dựng IJ vuông góc với d, từ J bạn dựng đường thẳng song song với ∆ và cắt ∆’ tại H, từ H dựng HM // IJ

    Khi đó, HM chính là đoạn vuông góc chung và d (∆, ∆’) = HM = IJ.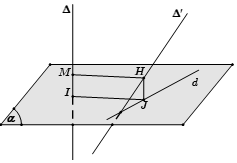Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó, d (∆, ∆’) = d (∆’, (α)).

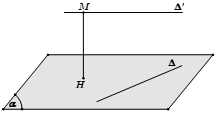
    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Phương pháp 3: Dựng 2 mặt phẳng song song và lần lượt chứa 2 đường thẳng. Khoảng cách giữa 2 mặt phẳng đó chính là khoảng cách giữa 2 đường thẳng cần tìm.

    Lưu ý: Phương pháp này thường sử dụng trong trường hợp khi kẻ đường thẳng song song với 1 trong 2 đường đề bài cho ban đầu gặp khó khăn.

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Phương pháp 4: Sử dụng phương pháp vec tơ

    * MN là đoạn vuông góc chung của AB và CD khi và chỉ khi:

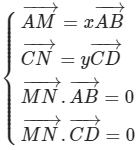
    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    * Nếu trong mặt phẳng (α) có hai véc tơ không cùng phương thì:

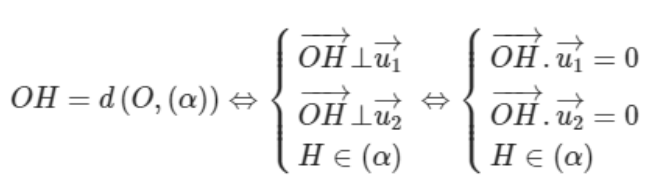
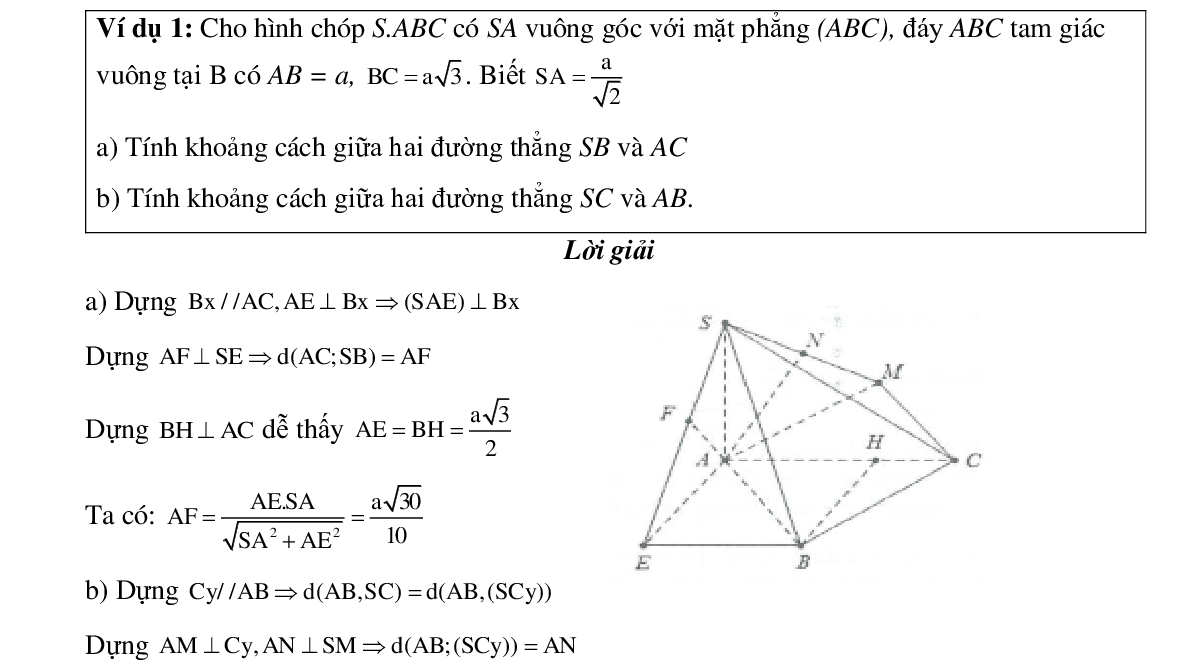
    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    3. Bài tập vận dụng

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Khoảng cách giữa 2 đường thẳng chéo nhau: Lý thuyết, cách xác định và các dạng bài tập (ảnh 1)

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 179 05/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: