Số nguyên tố là gì? Bảng tổng hợp các số nguyên tố nhỏ hơn 1000
Với tài liệu về Số nguyên tố bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.
Số nguyên tố
I. Lý thuyết Số nguyên tố
1. Số nguyên tố là gì?
Số nguyên tố là một tập hợp dãy số nguyên lớn hơn 1 chỉ chia hết được nó và 1. Nói cách khác, các số thuộc tập N lớn hơn 1 và chỉ chia hết được cho nó thì đó là số nguyên tố. Ví dụ số 3, chỉ chia hết cho 1 và nó. Tương tự như vậy, các số như 11, 13, 17, 19,... là số nguyên tố.
2. Đặc tính của số nguyên tố
Số nguyên tố có các đặc tính gồm:
-
Không bao gồm số 1.
-
Các số nguyên tố đều không chia hết cho 2 trừ số 2.
-
Dãy số nguyên tố là vô cực, không có giới hạn tương tự như tập N.
-
Ước bé nhất của số bất kỳ thuộc tập N luôn là số nguyên tố. Ví dụ 15 chia hết cho 3 (ước nhỏ nhất của 15), 3 là số nguyên tố.
-
Số X có ước nhỏ nhất là số dương, số này khác 1 và nhỏ hơn căn bậc hai của X thì đó chính là số nguyên tố. Ví dụ 30 có ước nhỏ nhất là 5, tính chất của 5 khác 1 vả nhỏ hơn căn bậc 2 của 30 thì lúc này 5 được xác định là số nguyên tố.
3. Thừa số nguyên tố
Thừa số nguyên tố là thừa số, nhưng là các số nguyên tố. Đây cách gọi của số nguyên tố khi sử dụng trong phép nhân các số nguyên tố, chẳng hạn: "Tích các thừa số nguyên tố".
Ví dụ:
6 = 2 x 3 trong đó 2 và 3 là các số nguyên tố.
105 = 3 x 5 x 7 trong số 3, 5 và 7 là các số nguyên tố.
4. Những định nghĩa khác liên quan tới số nguyên tố
a) Hai số nguyên tố được gọi là số nguyên tố cùng nhau nếu như chúng có ước số chung lớn nhất (số dương lớn nhất là mà hai số được đề cập đều chia hết cho nó) là 1.
Lưu ý: hai số nguyên tố gọi là cùng nhau có thể không phải đều là các số nguyên tố (chẳng hạn số 7 và số 8), chỉ cần thỏa mãn có ước chung lớn nhất là 1.
Ví dụ:
2 và 3 là số nguyên tố cùng nhau vì chúng có ước số chung lớn nhất là 1.
5 và 7 là hai số nguyên tố cùng nhau vì chúng có ước số chung lớn nhất là 1.
6 và 27 không phải là hai số nguyên tố cùng nhau vì ước số chung lớn nhất của chúng là 3 (khác 1)
b) Một số a được gọi là số siêu nguyên tố khi ta bỏ một số tùy ý các chữ số bên phải của a thì phần còn lại của a vẫn tạo thành một số nguyên tố.
Ví dụ:
37337 là một số siêu nguyên tố, vì khi bỏ một chữ số 7 bên tay trái số này đu, ta được số 3733 vẫn là một số nguyên tố.
c) Dãy số nguyên tố: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 là dãy số A000040 trong bảng OEIS.
d) Tập hợp số nguyên tố ký hiệu là P (Prime Number).
II. Cách tìm số nguyên tố
Cách 1: Kiểm tra số nguyên tố
-
Khi kiểm tra số nguyên tố, nếu số đó nhỏ hơn 2 thì đó không phải số nguyên tố.
-
Khi đếm số ước của số n trong đoạn từ 2 đến căn bậc hai của n mà số đó không có ước nào trong đoạn này thì nó là số nguyên tố. Còn nếu có thì nó đó không phải là số nguyên tố.
Cách 2: Chia thử nghiệm
Cách này được thực hiện bằng cách chia số cần kiểm tra theo lý thuyết số nguyên tố là được, tức là chia n cho tát cả các số nguyên từ 2 đến căn bậc 2 của n. Nếu có bất kỳ số nguyên nào mà n chia hết cho nó thì n là hợp số, còn không có thì n là số nguyên tố.
Đây là phương pháp đơn giản nhưng tốn thời gian, có thể kéo theo nhiều sai số trong quá trình thực hiện vì số phép chia sẻ tăng dần theo cấp số nhân khi số chữ số của số nguyên đó ngày càng nhiều.
Cách 3: Dùng thao tác lập từng phần tử với bước nhảy 1
Để kiểm tra số n có phải số nguyên tố hay không, bạn có thể sử dụng công cụ tính toán - máy tính cầm tay để xác định qua các bước sau:
Bước 1: Nhập vào số n
Bước 2: Kiểm tra nếu n < 2 thì n không phải là số nguyên tố.
Bước 3: Lặp từ 2 tới (n - 1). Nếu trong khoảng này tồn tại số mà n chia hết cho nó thì n không phải là số nguyên tố còn nếu chia hết thì n là số nguyên tố.
Cách 4: Dùng thao tác lặp từng phần tử với bước nhảy 2
Vì 2 là số nguyên tố chẵn duy nhất nên ta sẽ loại số 2 ra khỏi vòng lặp và bạn chỉ cần kiểm tra các số lẻ trong vòng lặp.
III. Bảng số nguyên tố nhỏ hơn 1000
| 2 | 79 | 191 | 311 | 439 | 577 | 709 | 857 |
| 3 | 83 | 193 | 313 | 443 | 587 | 719 | 859 |
| 5 | 89 | 197 | 317 | 449 | 593 | 727 | 863 |
| 7 | 97 | 199 | 331 | 457 | 599 | 733 | 877 |
| 11 | 101 | 211 | 337 | 461 | 601 | 739 | 881 |
| 13 | 103 | 223 | 347 | 463 | 607 | 743 | 883 |
| 17 | 107 | 227 | 349 | 467 | 613 | 751 | 887 |
| 19 | 109 | 229 | 353 | 479 | 617 | 757 | 907 |
| 23 | 113 | 233 | 359 | 487 | 619 | 761 | 911 |
| 29 | 127 | 239 | 367 | 491 | 631 | 769 | 919 |
| 31 | 131 | 241 | 373 | 499 | 641 | 773 | 929 |
| 37 | 137 | 251 | 379 | 503 | 643 | 787 | 937 |
| 41 | 139 | 257 | 383 | 509 | 647 | 797 | 941 |
| 43 | 149 | 263 | 389 | 521 | 653 | 809 | 947 |
| 47 | 151 | 269 | 397 | 523 | 659 | 811 | 953 |
| 53 | 157 | 271 | 401 | 541 | 661 | 821 | 967 |
| 59 | 163 | 277 | 409 | 547 | 673 | 823 | 971 |
| 61 | 167 | 281 | 419 | 557 | 677 | 827 | 977 |
| 67 | 173 | 283 | 421 | 563 | 683 | 829 | 983 |
| 71 | 179 | 293 | 431 | 569 | 691 | 839 | 991 |
| 73 | 181 | 307 | 433 | 571 | 701 | 853 | 997 |
IV. Các dạng bài tập về số nguyên tố
Dạng 1. Phân tích thừa số nguyên tố
Phân tích thừa số nguyên tố là bạn sẽ đi tìm đâu là con số không thể chia hết được cho ước chung nhỏ nhất. Lúc này, ban cần xem xét số A đề bài cho có chia được hết cho 2 hay không, sau đó lần lượt với số 3, 5,... trên bảng số nguyên tố. Cuối cùng, bạn lấy các thừa số nhân cho nhau.
Dạng 2. Tm ước số chung lớn nhất
Dạng tìm ước chung lớn nhất cũng thường xuất hiện trong các bài toán của số nguyên tố. Khi đó, một số được cho trong đề bài có thể sở hữu nhiều ước chung với ký hiệu là ƯCLN (a,b), trong đó a, b là số cần phải tìm ước chung. Để giải quyết bài này, bạn hãy lập tích các thừa số nguyên tố và lấy số mũ nhỏ nhất.
Ví dụ 1: Cho hai số 7 và 8. Hỏi hai số đó có phải là số nguyên tố cùng nhau hay không?
Lời giải:
- Ta có: 7 = 1 x 7, 8 = 1 x 2 x 2 x 2
- Nhận thấy ước chung lớn nhất của 7 và 8 là 1. Như vậy có thể kết luận 7 và 8 là hai số nguyên tố cùng nhau.
Ví dụ 2: Cho p và 2p + 1 đều là số nguyên tố (p > 5). Hỏi 4p + 1 là số nguyên tố hay hợp số.
Lời giải
Do p là số nguyên tố lớn hơn 3 nên p không chi hết cho 3 suy ra 4p cũng không chia hết cho 3.
Do 2p + 1 là số nguyên tố lớn hơn 3 nên 2p + 1 không chia hết cho 3 suy ra 2 x (2p + 1) không chia hết cho 3 hay 4p + 2 không chia hết cho 3. Mặt khác trong 3 số tự nhiên liên tiếp 4p, 4p + 1, 4p + 2 có một số chia hết cho 3 do đó 4p +1 chia hết cho 3, mà 4p + 1 > 3 suy ra 4p + 1 là hợp số.
V. Bài tập vận dụng
Bài 1: Cho p và p + 4 là số nguyên tố (p > 3) chứng tỏ rằng p + 8 là hợp số.
Lời giải
Vì p là số nguyên tố lớn hơn 3 nên p = 3k + 1 hoặc p = 3k + 2
Nếu p = 3k + 2 thì p + 4 = 3k + 6 chia hết cho 3 => loại
Nếu p = 3k + 1 thì p + 7 = 3k + 8 không chia hết cho 3 => 2 x (3k + 7) không chia hết cho 3 hay 2p + 14 không chia hết cho 3 mà trong ba số tự nhiên liên tiếp có một số chia hết cho 3 mà 2p + 14 và 2p + 15 không chia hết cho 3 suy ra 2p + 16 chia hết cho 3 hay p + 8 chia hết cho 3
Suy ra p + 8 là một hợp số.
Bài 2: Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê các cặp số nguyên tố sinh đôi nhỏ hơn 40. Có tất cả bao nhiêu cặp?
Giải:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40:
+) 3 và 5
+) 5 và 7
+) 11 và 13
+) 17 và 19
+) 29 và 31
Vậy có tất cả 5 cặp.
Bài 4: Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hàng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng, sao cho mỗi hàng có số người như nhau?
Giải:
Ta có: 33 = 3 . 11
Vì xếp 33 chiến sĩ thành các hàng thì số hàng là ước của 33
Ư(33) = 1; 3; 11; 33.
Với số hàng là 1 thì số người mỗi hàng là: 33 : 1 = 33 (người)
Với số hàng là 3 thì số người mỗi hàng là: 33 : 3 = 11 (người)
Với số hàng là 11 thì số người mỗi hàng là: 33 : 11 = 3 (người)
Với số hàng là 33 thì số người mỗi hàng là: 33 : 33 = 1 (người)
Vậy có 4 cách cách sắp xếp 33 chiến sĩ thành các hàng.
Bài 5: Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau, số người trong một nhóm là các số nguyên tố. Hỏi có bao nhiêu cách chia?
Giải:
Phân tích 30 ra thừa số nguyên tố ta được: 30 = 2.3.5
Vì cô giáo muốn chia lớp 30 học sinh thành các nhóm, các nhóm có số người bằng nhau nên số người của mỗi ngóm là ước của 30.
Mà số người mỗi nhóm là số nguyên tố nên số người mỗi nhóm là ước nguyên tố của 30.
Ta có bảng sau:
|
Số nhóm |
Số người một nhóm |
|
30:2 = 15 |
2 |
|
30:3 = 10 |
3 |
|
30:5 = 6 |
5 |
Do đó có thể chia thành 15 nhóm, 10 nhóm hoặc 6 nhóm.
Bài 6: Tìm các số thích hợp điền vào ô trống trong sơ đồ sau:
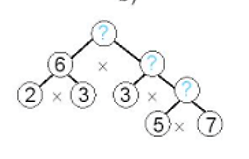
Bài 7: Tìm các số còn thiếu trong sơ đồ phân tích một số ra thừa số nguyên tố sau:
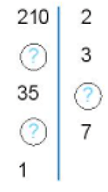
Bài 8: Hãy phân tích A = 42.95 ra thừa số nguyên tố.
Bài 9: Bạn Nam phân tích số 120 ra thừa số nguyên tố như sau: 120 = 23.3.5.
Bạn An phân tích 105 ra thừa số nguyên tố như sau: 105 = 3.5.7.
Chọn đáp án đúng.
A. Bạn Nam;
B. Bạn An;
C. Cả Nam và An đều sai.
D. Cả Nam và An đều đúng.
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Tổng hợp các đề đọc - hiểu có đáp án chi tiết
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)
