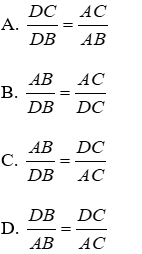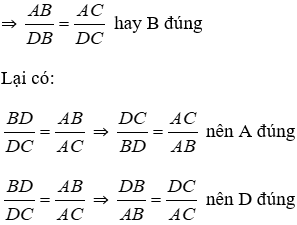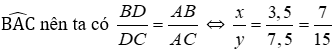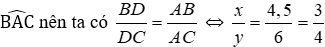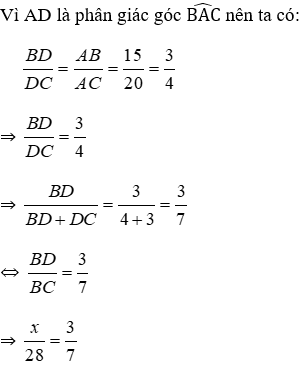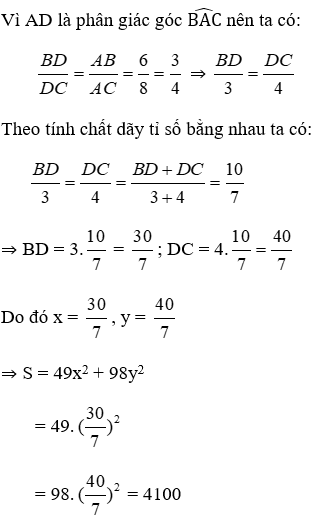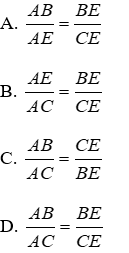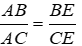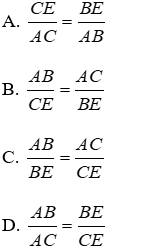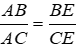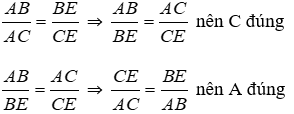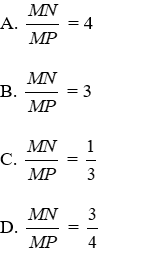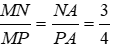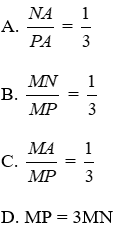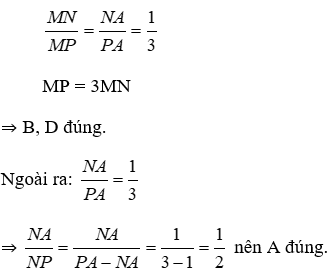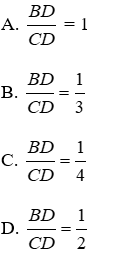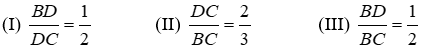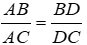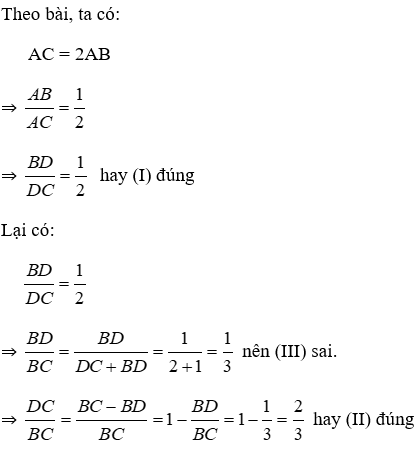Tia phân giác là gì? Thế là nào đường phân giác? Tính chất đường phân giác trong tam giác

Đường phân giác của tam giác

I. Tia phân giác là gì?

1. Định nghĩa tia phân giác

Tia phân giác của một góc là tia xuất phát từ đỉnh của góc và chia góc đó thành hai phần bằng nhau.

- Mỗi góc (không phải là góc bẹt) chỉ có một tia phân giác

​* Định lí thuận:

Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

* Định lí đảo:

- Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

- Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.

2. Đặc điểm của tia phân giác

• Độ chính xác: Tia phân giác chia một góc thành hai góc bằng nhau một cách chính xác, điều này rất quan trọng cho việc tính toán và vẽ hình.

• Vai trò trong tam giác: Trong bất kỳ tam giác nào, ba tia phân giác (kéo dài từ các đỉnh đến các cạnh đối diện) luôn giao nhau tại một điểm đặc biệt gọi là tâm của đường tròn nội tiếp. Đây là điểm từ đó có thể vẽ một đường tròn tiếp xúc với tất cả các cạnh của tam giác.

3. Cách nhận biết và vẽ tia phân giác

Tia phân giác chia một góc thành hai góc con có kích thước bằng nhau, có nghĩa là nếu bạn có góc ∠ABC, tia phân giác sẽ chia góc này thành hai góc con ∠ABD và ∠DBC sao cho: ∠ABD = ∠DBC.

Các bước để vẽ tia phân giác của một góc:

Bước 1: Vẽ một góc với đỉnh B và hai cạnh góc như BA và BC.

Bước 2: Dùng dụng cụ đo góc hoặc phần mềm vẽ hình học để xác định kích thước của góc ∠ABC. Ghi lại kích thước này để so sánh sau.

Bước 3: Xác định tia phân giác bằng cách sử dụng thước kẻ hoặc phần mềm vẽ hình học để chia góc ∠ABC thành hai phần bằng nhau. Đánh dấu điểm trên cạnh góc sao cho hai phần góc có kích thước đồng đều.

Bước 4: Vẽ một tia từ đỉnh của góc đi qua điểm đã đánh dấu. Tia này chính là tia phân giác, chia góc ∠ABC thành hai góc con bằng nhau.

Bước 5: Kiểm tra kết quả. Đảm bảo hai góc con do tia phân giác tạo ra là bằng nhau bằng cách đo lại bằng thước đo góc.

4. Ứng dụng của tia phân giác

*Ứng dụng giải toán hình học của tia phân giác

Trong toán học, đặc biệt là hình học, dùng tia phân giác có thể giải quyết các bài toán liên quan đến góc và tam giác.

Chứng minh tính chất góc: Tia phân giác được dùng để chứng minh hai góc bằng nhau hoặc để tìm ra các góc trong các bài toán hình học phức tạp. Ví dụ, trong tam giác, nếu một đường phân giác chia một góc thành hai phần bằng nhau, nó có thể được sử dụng để chứng minh rằng hai đoạn thẳng đối diện cũng có tỉ lệ nhất định, thông qua định lý đường phân giác.

Xác định tâm đường tròn nội tiếp: Trong một tam giác, ba tia phân giác của ba góc sẽ cắt nhau tại một điểm gọi là tâm đường tròn nội tiếp. Điểm này rất quan trọng có thể xác định vị trí và kích thước của đường tròn nội tiếp tam giác, giúp tính toán dễ dàng hơn trong các bài toán liên quan đến diện tích và chu vi.

Giải quyết bài toán đối xứng: Tia phân giác thường được sử dụng để tạo ra các bài toán về đối xứng trong hình học.

*Ứng dụng trong kiến trúc và kỹ thuật của tia phân giác

Ngoài toán học, tia phân giác cũng có nhiều ứng dụng trong kiến trúc và kỹ thuật:

Thiết kế kiến trúc: Tia phân giác được dùng trong thiết kế kiến trúc để tạo ra những cấu trúc đối xứng và cân đối. Việc áp dụng tia phân giác giúp kiến trúc sư đảm bảo các góc và cạnh được phân chia một cách chính xác, từ đó tạo ra các công trình hài hòa về mặt thẩm mỹ.

Kỹ thuật cơ khí: Trong kỹ thuật cơ khí, ứng dụng tia phân giác là gì? Tia phân giác có thể dùng để đảm bảo độ chính xác trong việc lắp ráp các bộ phận máy móc. Điều này giúp cải thiện hiệu suất và độ bền của các thiết bị cơ khí.

Thiết kế sản phẩm: Trong thiết kế sản phẩm, tia phân giác giúp các nhà thiết kế tạo ra các sản phẩm có tính thẩm mỹ và chức năng tốt hơn, đặc biệt là trong việc phân chia không gian hoặc tạo ra các góc cân đối.

*Ứng dụng trong đời sống của tia phân giác

Tia phân giác cũng xuất hiện trong nhiều tình huống hàng ngày mà chúng ta có thể không để ý:

Trang trí nội thất: Trong trang trí nội thất, ứng dụng tia phân giác là gì? Tia này giúp tạo ra các không gian cân đối và hài hòa. Điều này có thể được thấy rõ trong việc bố trí đồ nội thất sao cho không gian sống trở nên thoải mái và đẹp mắt hơn.

Thiết kế đồ họa: Tia phân giác dùng trong thiết kế đồ họa để tạo ra các tác phẩm nghệ thuật đối xứng và cân đối, từ logo đến poster.

Giáo dục: Trong giảng dạy toán học, tia phân giác có thể sử dụng như một công cụ để giảng giải các khái niệm hình học cho học sinh, giúp họ hiểu rõ hơn về các nguyên lý và định lý trong toán học.

II. Thế nào là đường phân giác?

1. Định nghĩa đường phân giác

Đường phân giác của một tam giác là đoạn thẳng xuất phát từ một đỉnh và chia góc tại đỉnh đó thành hai góc bằng nhau. Đồng thời, nó cắt cạnh đối diện tại điểm mà từ đó, tỉ lệ giữa các đoạn của cạnh đối diện bằng tỉ lệ giữa các cạnh còn lại của tam giác.

2. Tính chất đường phân giác trong tam giác

- Chia góc thành 2 phần bằng nhau: Tính chất nổi bật của tia phân giác là khả năng chia góc tại đỉnh tam giác thành hai góc bằng nhau. Việc hiểu về tia phân giác và đường phân giác giúp bạn dễ dàng chứng minh rằng các góc con tạo bởi tia phân giác là bằng nhau, từ đó hỗ trợ trong việc giải quyết các bài toán liên quan đến góc trong tam giác.

- Tính tỉ lệ cạnh đối diện: Đường phân giác trong tam giác chia cạnh đối diện thành hai đoạn có tỷ lệ tương đương với các cạnh còn lại của tam giác. Cụ thể, nếu đường phân giác cắt cạnh đối diện tại điểm D, thì tỷ lệ của các đoạn BD và DC sẽ bằng tỷ lệ của các cạnh còn lại của tam giác, được thể hiện qua công thức: AC/AB = DC/BD.

- Điểm giao của các đường phân giác: Trong tam giác, ba đường phân giác giao nhau tại một điểm đặc biệt gọi là tâm của đường tròn nội tiếp. Từ điểm này, bạn có thể vẽ một đường tròn tiếp xúc với tất cả các cạnh của tam giác.

3. Ứng dụng của tính chất đường phân giác

Chứng minh định lí: Tính chất của đường phân giác được sử dụng để chứng minh nhiều định lý hình học, như định lý về tỷ lệ phân chia cạnh đối diện và các bài toán liên quan đến góc trong tam giác.

Giải quyết bài toán: Trong các bài toán liên quan đến tam giác, đặc biệt khi tính toán tỷ lệ các đoạn và góc, việc nắm vững tính chất của đường phân giác sẽ giúp bạn giải quyết bài toán một cách chính xác và hiệu quả.

Thiết kế kiến trúc: Hiểu rõ về tia phân giác có thể được áp dụng trong thiết kế kiến trúc để tạo ra các cấu trúc đối xứng và cân đối hơn.

III. Phân biệt tia phân giác và đường phân giác

Tia phân giác: Là một tia xuất phát từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Tia phân giác không phải là một đoạn thẳng có độ dài cố định mà là một phần của đường thẳng kéo dài vô hạn.

Đường phân giác: Trong một tam giác, đường phân giác là đoạn thẳng nối từ một đỉnh tam giác đến điểm cắt của tia phân giác với cạnh đối diện. Đường phân giác là một đoạn thẳng có độ dài xác định và chia cạnh đối diện tam giác theo tỷ lệ nhất định.

Mối quan hệ: Tia phân giác là thành phần cơ bản có thể dựa vào từ đó xác định đường phân giác. Đường phân giác chính là đoạn thẳng mà tia phân giác cắt cạnh đối diện tam giác, và nó chia cạnh đối diện thành hai phần tương ứng.

IV. Các dạng bài tập về tia phân giác, đường phân giác

Dạng 1. Chứng minh một tia phân giác của một góc cho trước

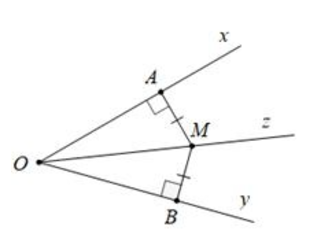
Phương pháp giải: Chứng minh tia Oy là tia phân giác của góc xOz

- Cách 1. Chứng minh tia Oy nằm giữa hai tia Ox và Oz

Chứng minh góc xOy = góc yOz

- Cách 2: Chứng minh góc xOy = góc yOz = 1/2 góc xOz

- Cách 3: Dùng tính chất đường trung tuyến trong tam giác cân đồng thời là đường phân giác

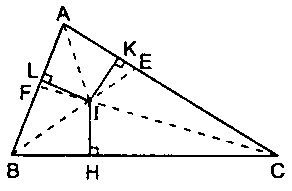
Ví dụ: Cho tam giác ABC vuông tại A . Từ một điểm K bất kì trên cạnh BC, kẻ KH vuông góc AC (H thuộc AC). Trên tia đối của tuan HK lấy điểm I sao cho HI = HK. Chứng minh:

a. AB // HK

b. góc KAH = góc IAH

c. tam giác AKI cân

Hướng dẫn giải

a. Ta có: AB vuông góc AC (tam giác ABC vuông tại A),

KH vuông góc AC (giả thiết)

=> AB // KH (từ vuông góc đến song song)

b. Xét tam giác AHK và tam giác AHI, có:

Hk = HI (giả thiết)

góc AHK = góc AHI = 90 (giả thiết)

AH chung

Do đó, tam giác AHK = tam giác AHI (hai cạnh góc vuông)

=> góc KAH = góc IAh (hai góc tương ứng)

c. Theo câu b, ta có: tam giác AHK = tam giác AHI => AK = AI (hai cạnh tương ứng)

=> tam giác AKI cân tại A.

Dạng 2. Tính số đo góc

Ví dụ: Cho hai góc xOy và góc yOz là hai góc kề bù, biết góc xOy = 120⁰

a. Tính góc yOz

b. Gọi Om là tia phân giác của góc xOy. Tính góc zOm

Hướng dẫn giải

a. Vì góc xOy và góc yOz là hai góc kề bù nên ta có góc xOy + góc yOz = 180 hay góc yOz = 180 - góc xOy = 60

b. Tia Om là tia phân giác của góc xOy nên góc xOm = mOy = góc xOy / 2 = 120/2 = 60

Hai góc xOm và zOm kề bù nên góc xOm + góc zOm = 180

=> góc zOm = 120

Dạng 3. Vận dụng tính chất của một góc để chứng minh các đoạn thẳng bằng nhau

Phương pháp giải: Áp dụng định lí thuận: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

Ví dụ: Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường thẳng vuông góc với BC tại trung điểm của BC ở D. Gọi H và K là chân các đường vuông góc kẻ từ D đến các đường thẳng AB, AC. Chứng minh: BH = CK.

Hướng dẫn giải

TA có: D thuộc phân giác của góc A

DH vuông góc với AB, DK vuông góc với AC

=> DH = DK (tính chất tia phân giác của một góc)

Gọi G là trung điểm của BC

Xét tam giác BGD và tam giác CGD, ta có:

góc BGD = góc CGD = 90° (DG là đường trung trực của BC)

BG = CG (giả thiết)

DG là cạnh chung

Do đó, tam giác BGD = tam giác CGD (hai cạnh góc vuông)

=> BD = CD (hai cạnh tương ứng)

Xét tam giác BHD và tam giác CKD có:

góc BHD = CKD = 90°

DH = DK (chứng minh trên)

BD = CD (chứng minh trên)

Do đó, tam giác BHD = tam giác CKD (cạnh huyền - cạnh góc vuông)

=> BH = CK (hai cạnh tương ứng)

V. Bài tập về đường phân giác

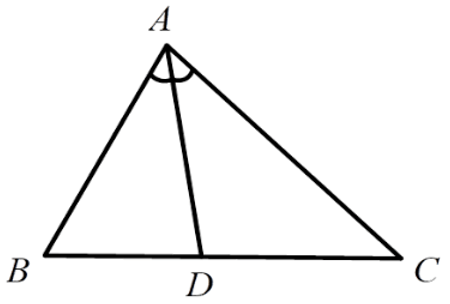
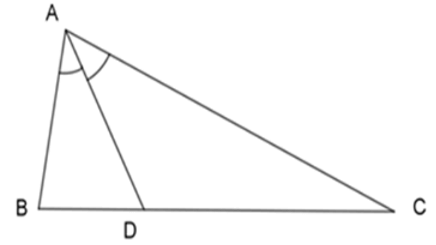
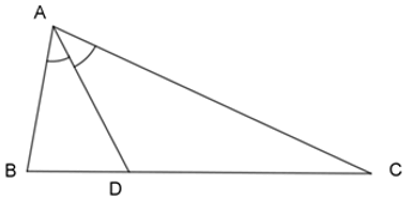
Bài 1: Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu đúng:

Lời giải

Vì AD là phân giác góc 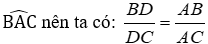(tính chất đường phân giác của tam giác).

Đáp án cần chọn là: B

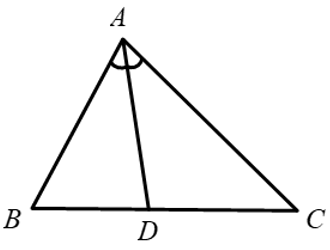
Bài 2: Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu sai:

Lời giải

Vì AD là phân giác góc 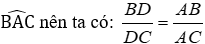(tính chất đường phân giác của tam giác).

Chỉ có C sai

Đáp án cần chọn là: C

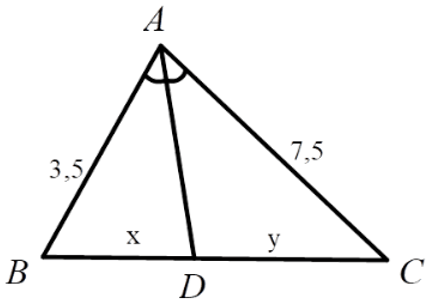
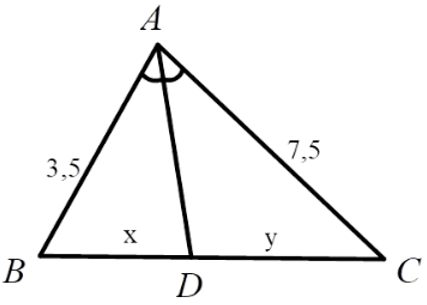
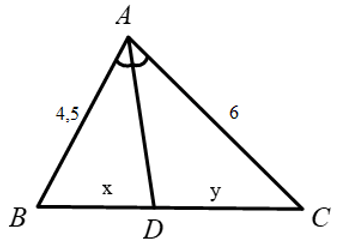
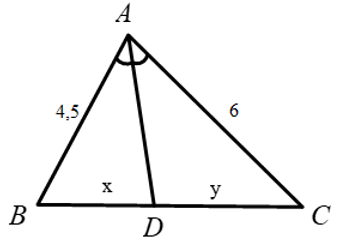
Bài 3: Hãy chọn câu đúng. Tỉ số x/y của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.

Lời giải

Xét tam giác ABC, vì AD là phân giác góc

Đáp án cần chọn là: A

Bài 4: Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số x/y bằng:

Lời giải

Xét tam giác ABC, vì AD là phân giác góc

Đáp án cần chọn là: A

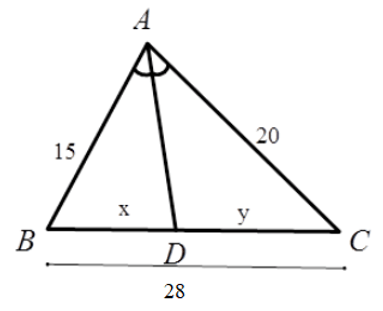
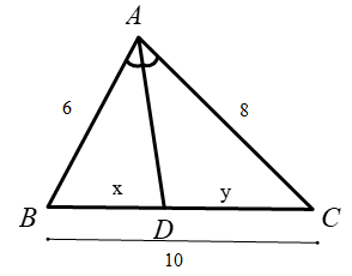
Bài 5: Hãy chọn câu đúng. Tính độ dài x, y của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là cm.

A. x = 16cm; y = 12cm

B. x = 14cm; y = 14cm

C. x = 14,3cm; y = 10,7cm

D. x = 12cm; y = 16cm

Lời giải

⇒ x = 12cm ⇒ y = 28 – x = 16 cm

Vậy x = 12cm; y = 16cm

Đáp án cần chọn là: D

Bài 6: Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức S = 49x² + 98y².

A. 3400

B. 4900

C. 4100

D. 3600

Lời giải

Vậy S = 4100

Đáp án cần chọn là: C

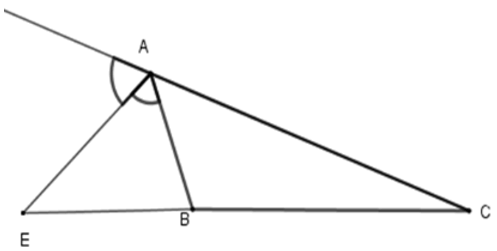
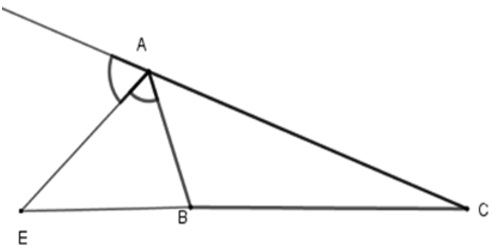
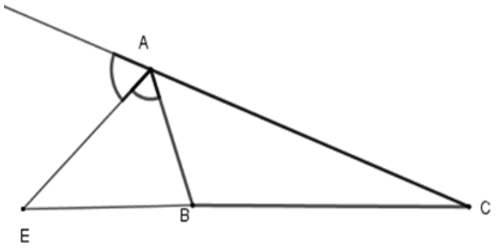
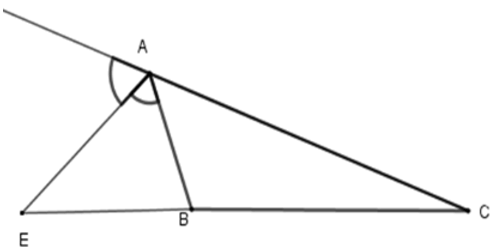
Bài 7: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:

Lời giải

Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên

Đáp án cần chọn là: D

Bài 8: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:

Lời giải

Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên

Chỉ có B sai.

Đáp án cần chọn là: B

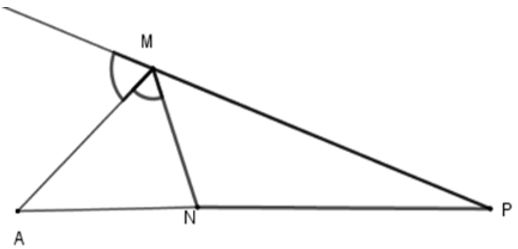
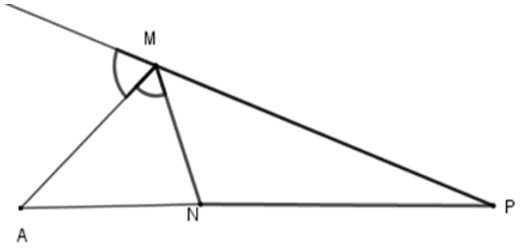
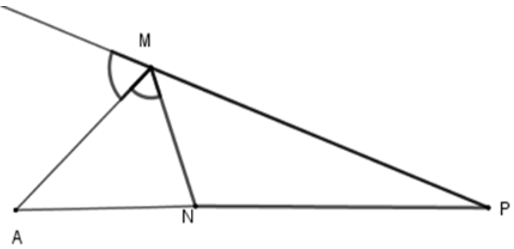
Bài 9: Cho ΔMNP, MA là phân giác ngoài của góc M, biết 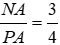. Hãy chọn câu đúng:

Lời giải

Theo tính chất đường phân giác của tam giác ta có

Đáp án cần chọn là: D

Bài 10: Cho ΔMNP, MA là phân giác ngoài của góc M, biết 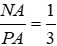. Hãy chọn câu sai:

Lời giải

Theo tính chất đường phân giác của tam giác ta có:

Chỉ có C sai.

Đáp án cần chọn là: C

Bài 11: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC, khi đó ?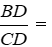

Lời giải

Đáp án cần chọn là: D

Bài 12: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Xét các khẳng định sau, số khẳng định đúng là:

A. 0

B. 3

C. 1

D. 2

Lời giải

Vì AD là đường phân giác của tam giác ABC nên:

Vậy chỉ có 2 khẳng định đúng.

Đáp án cần chọn là: D

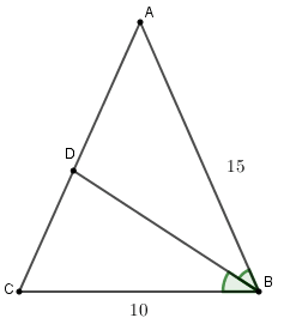
Bài 13: Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?

A. 3cm

B. 6cm

C.9cm

D. 12cm

Lời giải

Mà tam giác ABC cân tại A nên AC = AB = 15cm

Đáp án cần chọn là: C

Xem thêm:

Trắc nghiệm Định lí Ta-lét trong tam giác

Trắc nghiệm Khái niệm hai tam giác đồng dạng