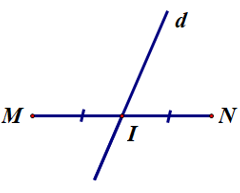Nội dung bài viết

    Xem thêm

    Lý thuyết, cách xác định và bài tập các cách chứng minh một đường thẳng là đường trung trực của tam giác

    Với tài liệu về các t cách chứng minh một đường thẳng là đường trung trực của tam giác bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.

     

    1 134 05/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Chứng minh một đường thẳng là đường trung trực của tam giác

    1. Phương pháp giải

    Để chứng minh đường thẳng d là đường trung trực của đoạn thẳng AB, ta sử dụng một trong hai cách sau:

    Cách 1 (dùng định nghĩa): Chứng minh đường thẳng d vuông góc với đoạn thẳng AB tại trung điểm M của đoạn thẳng AB;

    Cách 2 (dùng tính chất): Chứng minh đường thẳng d chứa hai điểm E, F cách đều A và B.

    Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    2. Ví dụ minh họa:

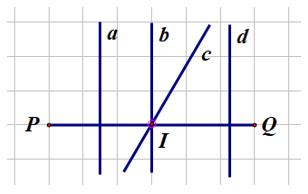
    Ví dụ 1. Cho hình vẽ bên.

    Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    Đường thẳng nào là đường trung trực của đoạn thẳng PQ?

    Hướng dẫn giải:

    Một đường thẳng là đường trung trực của một đoạn thẳng khi thỏa mãn cả hai yếu tố sau:

    + Đi qua trung điểm của đoạn thẳng.

    + Vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.

    - Ta thấy đường thẳng a và d không đi qua trung điểm I của đoạn thẳng PQ.

    Do đó đường thẳng a và d không phải là đường trung trực của đoạn thẳng PQ.

    - Đường thẳng b đi qua trung điểm I và vuông góc với đoạn thẳng PQ tại trung điểm I.

    Do đó đường thẳng b là đường trung trực của đoạn thẳng PQ.

    - Đường thẳng c đi qua trung điểm I nhưng không vuông góc với đoạn thẳng PQ tại trung điểm I.

    Do đó đường thẳng c không phải là đường trung trực của đoạn thẳng PQ.

    Vậy đường thẳng b là đường trung trực của đoạn thẳng PQ.

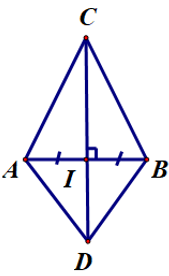
    Ví dụ 2. Cho ∆ABC có AC = BC. Gọi I là trung điểm AB. Trên tia CI lấy điểm D sao cho D nằm khác phía với C (bờ là đường thẳng AB). Chứng minh CD là đường trung trực của AB.

    Hướng dẫn giải:

    Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    Cách 1:

    Xét ∆CAI và ∆CBI, có:

    CA = CB (giả thiết).

    CI là cạnh chung.

    AI = BI (I là trung điểm AB).

    Do đó ∆CAI = ∆CBI (cạnh – cạnh – cạnh).

    Suy ra CIA^=CIB^ (cặp góc tương ứng).

    Mà CIA^+CIB^=180° (hai góc kề bù).

    Do đó CIA^=CIB^=90°.

    Khi đó ta có CI ⊥ AB.

    Mà I là trung điểm của AB (giả thiết).

    Suy ra CI là đường trung trực của AB.

    Vậy CD là đường trung trực của AB.

    Cách 2:

    Xét ∆ADC và ∆BDC, có:

    AC = BC (giả thiết).

    CD là cạnh chung.

    ACD^=BCD^ (∆CAI = ∆CBI).

    Do đó ∆ADC = ∆BDC (cạnh – góc – cạnh).

    Suy ra AD = BD (cặp cạnh tương ứng).

    Mà CA = CB (giả thiết).

    Vậy CD là đường trung trực của AB.

    3. Bài tập tự luyện

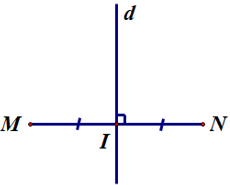
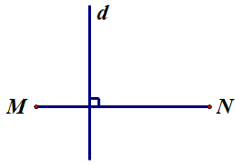
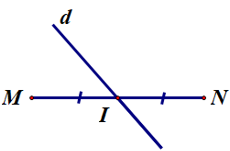
    Bài 1. Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?

    A.Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    B.Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    C.Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    D.Nhận biết và chứng minh một đường thẳng là đường trung trực của một đoạn thẳng (cách giải + bài tập)

    Bài 2. Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?

    A. AD vuông góc với BC;

    B. AD vuông góc với BE;

    C. AD là đường trung trực của đoạn thẳng BE;

    D. AD đi qua trung điểm của đoạn thẳng BE.

    Bài 3. Cho xOy^khác góc bẹt. Trên tia phân giác Ot của xOy^, lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?

    A.Ot vuông góc với AB;

    B.Ot là đường trung trực của đoạn thẳng AB;

    C. Ot đi qua trung điểm của AB;

    D. OAI^≠OBI^.

    Bài 4. Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?

    A. AM là đường trung trực của đoạn thẳng BC;

    B. AN là đường trung trực của đoạn thẳng BC;

    C. MN là đường trung trực của đoạn thẳng BC;

    D. Cả A, B, C đều đúng.

    Bài 5. Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.

    A. ADC^=ACD^;

    B. AK ⊥ DC;

    C. AK là đường trung trực của đoạn thẳng DC;

    D. Cả A, B, C đều đúng.

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 134 05/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: