Định lí Talet trong tam giác và trong hình thang (2024) và bài tập có đáp án

Định lí Talet trong tam giác và trong hình thang (2024) và bài tập có đáp án

I. Lý thuyết

1. Định lý Talet trong tam giác

1.1. Lý thuyết về tỷ số của hai đoạn thẳng

Lý thuyết về tỷ số của hai đoạn thẳng là một khái niệm quan trọng trong hình học và toán học. Nó giúp chúng ta so sánh độ dài của hai đoạn thẳng và xác định mối quan hệ tỷ lệ giữa chúng. Dưới đây là một số thông tin chi tiết về lý thuyết này:

Khái niệm về tỷ số của hai đoạn thẳng

Tỷ số của hai đoạn thẳng là một phép tính dựa trên độ dài của chúng. Để tính tỷ số, chúng ta cần đo độ dài của cả hai đoạn thẳng bằng cùng một đơn vị đo, ví dụ như centimet (cm) hoặc inch (in). Tỷ số của hai đoạn thẳng AB và CD thường được kí hiệu là $\frac{AB}{CD}$

Đoạn thẳng tỷ lệ:

Hai đoạn thẳng AB và CD được gọi là tỷ lệ với hai đoạn thẳng A'B' và C'D' nếu tồn tại một tỷ lệ thức tương đương giữa chúng. Điều này có nghĩa là tỷ số của đoạn AB và đoạn A'B' bằng tỷ số của đoạn CD và đoạn C'D'. Cụ thể, nếu $\frac{AB}{CD}=\frac{A\text{'}B\text{'}}{C\text{'}D\text{'}}$ thì ta nói AB và CD tỷ lệ với A'B' và C'D'.

Tính chất quan trọng:

Tính chất quan trọng của đoạn thẳng tỷ lệ là nó cho phép ta thể hiện sự tương quan tỷ lệ giữa các đoạn thẳng trong hình học. Nếu hai đoạn thẳng tỷ lệ với nhau, thì nếu chúng được mở rộng hoặc thu hẹp cùng một lượng, tỷ số của chúng vẫn không đổi.

Ví dụ: Nếu $\frac{AB}{CD}=\frac{A\text{'}B\text{'}}{C\text{'}D\text{'}}$thì $\frac{2AB}{2CD}=\frac{2A\text{'}B\text{'}}{2C\text{'}D\text{'}}$

Ứng dụng trong hình học và toán học:

Lý thuyết tỷ số của hai đoạn thẳng rất hữu ích trong hình học và toán học. Nó được sử dụng để giải quyết các bài toán liên quan đến tỷ lệ, tương tự và đối xứng trong hình học. Nó cũng thường xuất hiện trong các bài toán liên quan đến biến đổi đồ thị và giải tích.

Trong tổng quan, lý thuyết tỷ số của hai đoạn thẳng là một khái niệm quan trọng giúp chúng ta hiểu và xác định mối quan hệ tỷ lệ giữa các đoạn thẳng trong không gian hình học và toán học.

1.2. Định lý Talet trong hình tam giác

Định lý Talet thuận trong tam giác:

Giả sử chúng ta có một tam giác EFG và một đường thẳng F'G' song song với cạnh FG và cắt hai cạnh EF và EG tại các điểm F' và G' tương ứng.

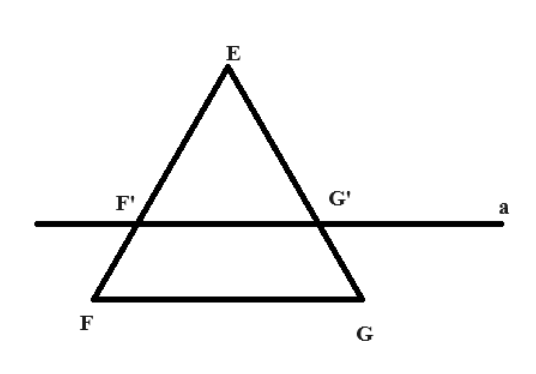
Khi đó, ta có các tỷ số sau:

$\frac{EF\text{'}}{EF}=\frac{EG\text{'}}{EG}$

$\frac{F\text{'}F}{EF}=\frac{G\text{'}G}{EG}$

$\frac{EF\text{'}}{FF\text{'}}=\frac{EG\text{'}}{GG\text{'}}$

​ Điều này có nghĩa rằng đoạn EF' và đoạn EG' có tỷ số độ dài bằng tỷ số độ dài của cạnh EF và cạnh EG. Tương tự, đoạn FF' và GG' cũng có tỷ số độ dài tương ứng với cạnh EF và cạnh EG.

Định lý Talet đảo:

Ngược lại, định lý Talet đảo khẳng định rằng nếu một đường thẳng cắt hai cạnh của tam giác và đoạn thẳng được định ra trên hai cạnh này có tỷ số độ dài tương ứng, thì đường thẳng đó sẽ song song với cạnh còn lại của tam giác.

Điều này được thể hiện bằng các tỷ số sau:

$\frac{EF\text{'}}{EF}=\frac{EG\text{'}}{EG}$

$\frac{EF\text{'}}{FF\text{'}}=\frac{EG\text{'}}{GG\text{'}}$

$\frac{FF\text{'}}{EF}=\frac{GG\text{'}}{EG}$

Khi điều kiện trên được thỏa mãn, ta có F'G' song song với FG

Hệ quả của định lý Talet:

Hệ quả quan trọng của định lý Talet là nếu một đường thẳng cắt hai cạnh hoặc phần kéo dài của hai cạnh của tam giác và song song với cạnh còn lại, thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỷ lệ với ba cạnh của tam giác ban đầu.

Cụ thể: $\frac{EF\text{'}}{EF}=\frac{EG\text{'}}{EG}=\frac{F\text{'}G\text{'}}{FG}$

Điều này đồng nghĩa với việc đường thẳng cắt tạo ra một tam giác tương tự (tam giác có các góc tương tự và các cạnh tỷ lệ với tam giác ban đầu).

2. Định lý Talet trong hình thang

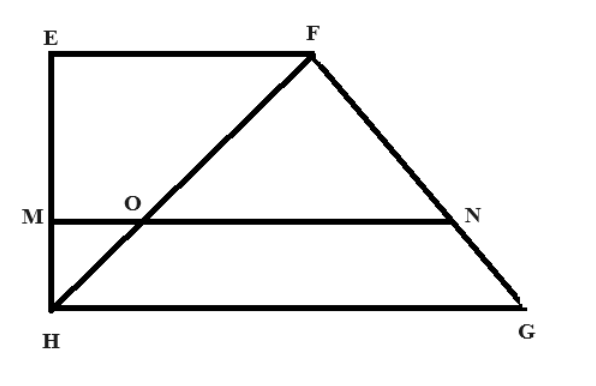
Giả sử chúng ta có một hình thang EFGH với hai đáy EF và GH, và điểm N thuộc đoạn FG và điểm M thuộc đoạn EH. Nếu đường thẳng MN song song với hai đáy EF và HG và cắt hai cạnh bên FG và EH lần lượt tại các điểm M và N, thì tỷ số giữa các đoạn thẳng tương ứng trên các đáy là bằng nhau:

$\frac{FN}{FG}=\frac{EM}{EH}$

Ngược lại, nếu tỷ số $\frac{FN}{FG}=\frac{EM}{EH}$ ​ , thì đường thẳng MN sẽ song song với đáy EF và HG của hình thang.

Áp dụng định lý Talet trong bài toán:

Giả sử chúng ta có một hình thang EFGH với đáy EF song song với đáy GH (EF < HG), và đường thẳng MN song song với đáy EF và GH. Đường thẳng MN cắt hai cạnh FG và EH lần lượt tại các điểm M và N. Biết rằng FG = 6 cm, FN = 4 cm và EH = 9cm chúng ta cần tìm độ dài của EM.

Lời giải:

Theo định lý Talet, chúng ta có:

$\frac{FN}{FG}=\frac{EM}{EH}$

​ Thay các giá trị đã biết vào phương trình:

$\frac{4}{6}=\frac{EM}{9}$

Bây giờ, để tìm độ dài BN, ta có thể giải phương trình:

4 x 9 = EM x 6

36 = EM x 6

EM = 6

Vậy độ dài của đoạn thẳng EM là 6 cm.

II. Bài tập vận dụng

Bài 1. Viết tỷ số của các cặp đoạn thẳng có độ dài như sau:

a) AB = 8 cm; CD = 9 cm.

Ta có:

$\frac{AB}{CD}=\frac{8}{9}$

$\frac{CD}{AB}=\frac{9}{8}$

b) EF = 6 dm, GH = 3 dm

Ta có:

$\frac{EF}{GH}=\frac{6}{3}=2$

$\frac{GH}{EF}=\frac{3}{6}=\frac{1}{2}$

c) MN = 18 cm; PQ = 6dm

Ta có:

$\frac{MN}{PQ}=\frac{18}{6}=3$

$\frac{PQ}{MN}=\frac{6}{18}=\frac{1}{3}$

Bài 2: Tìm giá trị của đoạn EB trên hình vẽ sau, biết Tam giác ABC là tam giác vuông tại B, có: AC = 10 dm, AE = 3 dm, AF = 4 dm và EF song song với BC

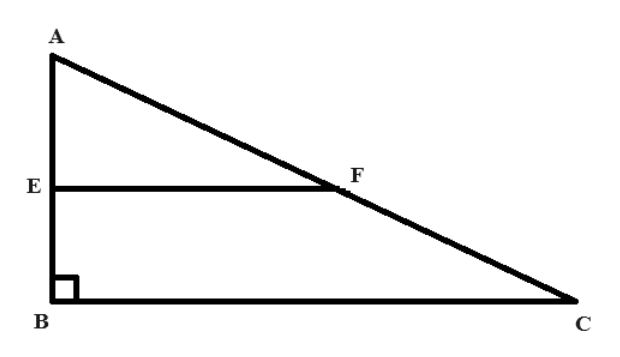
Lời giải:

Thấy: AF + FC = AC thì

4 + FC = 10

FC = 10 - 4 = 6 (dm)

Ta có EF song song với BC thì có các tỷ số như sau:

$\frac{AB}{BE}=\frac{AF}{FC}$

$\frac{3}{BE}=\frac{4}{6}$

4 x BE = 3 x 6

4 x BE = 18

BE = 4,5 (dm)

Đáp số: 4,5 dm

Bài 3:

Cho hình vẽ sau:

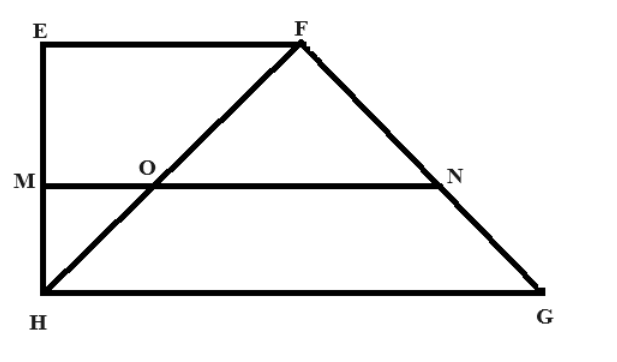
trong đó MN song song HG, FN = 12 cm, HM = 18 cm, FG= 36 cm. Độ dài EH bằng bao nhiêu?

Lời giải:

Ta có: MN song song với HG thì các tỷ số như sau:

$\frac{HM}{EH}=\frac{NG}{FG}$

Thay các số liệu vào:

$\frac{18}{EH}=\frac{36-12}{36}=\frac{24}{36}=\frac{2}{3}$

2 x EH = 18 x 3

2 x EH = 54

EH = 27 (cm)

Đáp số: 27 cm