Hợp số là gì? Đặc điểm, phân loại và ứng dụng của hợp số

Hợp số là gì? Đặc điểm, phân loại và ứng dụng của hợp số

1. Hợp số là gì?

Hợp số là một số tự nhiên lớn hơn 1 và có thể biểu diễn thành tích của hai số tự nhiên khác nhỏ hơn nó. Nói cách khác, hợp số là số chia hết cho các số khác ngoài 1 và chính nó.

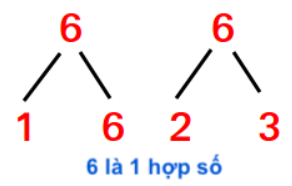
– Các số không phải là số nguyên tố là hợp số vì chúng chia hết cho nhiều hơn hai số.

– Mọi số nguyên dương bất kì đều có ba trường hợp xảy ra, hoặc là số nguyên tố, hoặc là hợp số, hoặc không phải là số nguyên tố cũng không phải là hợp số.

– Hợp số nhỏ nhất có 1 chữ số là số 4.

– Hợp số lớn nhất có 1 chữ số là số 9.

– Hợp số nhỏ nhất có 2 chữ số là số 10

– Hợp số lớn nhất có 2 chữ số là số 99

– Hợp số nhỏ nhất có 3 chữ số là số 100

– Hợp số lớn nhất có 3 chữ số là số 999

2. Đặc điểm của hợp số

+ Mọi số tự nhiên lớn hơn 1 không phải là số nguyên tố đều là hợp số.

+ Có vô số hợp số.

+ Mọi hợp số đều có ít nhất một ước số nguyên tố không vượt quá căn bậc hai của nó.

+ Hai hợp số bất kỳ luôn có ít nhất một ước số chung là 1.

+ Tích của hai số nguyên tố bất kỳ là một hợp số.

3. Tính chất của hợp số

• Phân tích ra thừa số nguyên tố

Một trong những tính chất quan trọng của hợp số là khả năng diễn giải thành ước nguyên tố, nghĩa là biểu diễn nó dưới dạng tích của các giá trị nguyên tố. Ví dụ, 18 có thể phân tích thành 2x3x3, với 2 và 3 được hiểu như các thừa số nguyên tố. Việc phân tích này giúp ta hiểu rõ hơn về cấu trúc của hợp số, đồng thời hỗ trợ trong những phép toán phức tạp hơn.

• Số ước

Hợp số là một thuật ngữ toán học gồm nhiều hơn 2 ước. Chẳng hạn, 15 sẽ có các ước cụ thể là 1, 3, 5 và 15. Tính chất này giúp phân biệt hợp số với nguyên tố. Ngoài ra, ước cũng cho thấy mức độ chia hết của thuật ngữ toán học này, đóng vai trò quan trọng trong nhiều dạng bài về chia hết và ước số.

• Không phải là số nguyên tố

Hợp số có thể chia hết cho ít nhất một số tự nhiên khác, trong khi số nguyên tố chỉ có khả năng chia hết cho 1 và chính bản thân nó. Điều này giúp khái niệm này nổi bật trong các bài toán về phân loại, hỗ trợ học sinh dễ dàng xác định một cách nhanh chóng và chính xác. Hiểu được tính chất này cũng giúp bạn dễ dàng phân tích, vận dụng vào bài tập hiệu quả hơn.

• Tính chất chia hết

Hợp số có tính chất chia hết cho ít nhất ba số, cụ thể là 1, chính nó cùng ít nhất một số khác. Nhờ vậy, khái niệm dễ dàng nhận biết trong các bài toán yêu cầu kiểm tra tính chia hết. Ví dụ, 15 chia hết cho 1, 3, 5 và 15, thể hiện rõ khả năng này và cho thấy sự khác biệt so với giá trị nguyên tố.

• Tích của các số nguyên tố

Mỗi hợp số đều có thể viết dưới dạng một phép nhân mà tích là các giá trị nguyên tố. Ví dụ, 30 có thể phân tích thành 2x3x5, trong đó 2, 3 và 5 là những số nguyên tố. Việc phân tích này không chỉ giúp ta hiểu rõ cấu trúc của khái niệm này, mà còn rất hữu ích trong các bài toán. Nó giúp ta dễ dàng xử lý những phép tính phức tạp và rút gọn các biểu thức toán học một cách chính xác.

4. Phân loại hợp số

Có hai loại hợp số đó là Hợp số lẻ và Hợp số chẵn.

– Hợp số có chữ số lẻ ở hàng đơn vị là hợp số lẻ. Nói một cách đơn giản, tất cả các số lẻ không phải là số nguyên tố đều là hợp số lẻ.

Ví dụ: 9, 15, 21, ...

– Hợp số có chữ số chẵn ở hàng đơn vị là hợp số chẵn. Nói một cách đơn giản, tất cả các số chẵn trừ 2 đều là hợp số chẵn. Điều này là do không có số chẵn nào (ngoại trừ 2) có thể là số nguyên tố.

Ví dụ: 8, 12, 14, ...

5. Cách kiểm tra hợp số

Chúng ta chỉ có thể kiểm tra một số có phải là hợp số hay không bằng cách: Nếu nhỏ hơn 2 thì chắc chắn số đó không phải là hợp số. Nếu đếm số ước của số n trong đoạn từ 2 cho đến căn bậc hai của n mà có ước thì n được coi là hợp số. Ngược lại, nếu không có thì nó là số nguyên tố.

Ngoài ra, chúng ta có thể kiểm tra một số có phải là hợp số hay không bằng 3 phương pháp sau:

Phương pháp 1: Kiểm tra một số có phải là hợp số hay không dựa theo thao tác lặp từng phần tử với bước nhảy 1.

Để kiểm tra N có phải là hợp số hay không bằng phương pháp này ta làm như sau:

– Bước 1: Nhập số N.

– Bước 2: Kiểm tra nếu N < 2 thì N không phải là một hợp số. Nếu N lớn 2 thì chuyển đến bước 3.

– Bước 3: Lặp trong khoảng từ 2 cho đến ( N – 1). Nếu trong khoảng này mà tồn tại số mà N chia hết cho số đó thì kết luận: N là hợp số. Nếu kết quả ngược lại thì N là một số nguyên tố.

Ví dụ: Kiểm tra xem 12 có phải là hợp số không?

Ta có: 12 > 2 và trong khoảng tử 2 đến 11, ta thấy rằng 12 chia hết cho 2 và 6.

Vì vậy chắc chắn 12 là hợp số.

Phương pháp 2: Kiểm tra một số có phải là hợp số hay không theo dấu hiệu chia hết cho 2; 3; 5; 9 mà chúng ta đã được học.

Ví dụ: Kiểm tra xem số 122 có phải là hợp số hay không?

Theo dấu hiệu chia hết cho 2 ta thấy số 120 ⋮ 2 nên số 120 có nhiều hơn 2 ước.

Vậy số 120 là hợp số.

Phương pháp 3:

Chúng ta cũng có thể dự vào bảng số nguyên tố để kiểm tra một số có phải là hợp số hay không bằng cách loại từ các số là số nguyên tố từ đó tìm ra hợp số. (Đây là cách được đánh giá là tối ưu hơn 2 phương pháp trên)

6. Ứng dụng của hợp số

Phân tích số

• Hợp số là công cụ thiết yếu để phân tích các số ra thừa số nguyên tố, giúp giải quyết nhiều bài toán và ứng dụng trong các lĩnh vực khác nhau.

• Ví dụ: Phân tích số 12 ra thừa số nguyên tố, ta có 12 = 2^2 x 3.

Chia hết

• Hợp số giúp ta xác định các số chia hết cho nhau.

• Ví dụ: Số 15 chia hết cho 3 vì 15 = 3 x 5, và 5 là hợp số.

Giải mã

• Hợp số được sử dụng trong các thuật toán mã hóa và giải mã, đảm bảo an toàn thông tin.

• Ví dụ: Hệ thống RSA sử dụng các số nguyên tố lớn để mã hóa thông tin.

Lý thuyết số

• Hợp số là chủ đề nghiên cứu quan trọng trong lý thuyết số, giúp giải mã các bí ẩn về các số tự nhiên.

• Ví dụ: Bảng nguyên tố được xây dựng dựa trên các số nguyên tố và hợp số.

7. Các dạng bài tập về hợp số

Dạng 1: Phân tích số ra thừa số nguyên tố

Ví dụ: Phân tích số 144 ra thừa số nguyên tố.

Lời giải:

144 | 2

72 | 2

36 | 2

18 | 2

9 | 3

3 | 3

1

Kết quả: 144 = 2 x 2 x 2 x 2 x 3 x 3 (hay 144 = 2⁴ x 3²).

Dạng 2: Tìm số nguyên tố nhỏ nhất chia hết cho n

Ví dụ: Tìm số nguyên tố nhỏ nhất chia hết cho 20.

Lời giải:

• Liệt kê các số nguyên tố bé hơn hoặc bằng 20: 2, 3, 5, 7, 11, 13, 17, 19.

• 20 chia hết cho 2.

Kết quả: Số nguyên tố nhỏ nhất chia hết cho 20 là 2.

Dạng 3: Tìm số ước số của một hợp số

Ví dụ: Tìm số ước số của số 30.

Lời giải:

• Số ước số của một hợp số có dạng n = (a + 1)(b + 1), với a và b là các số mũ trong phân tích thừa số nguyên tố của hợp số đó.

• 30 = 2 * 3 * 5 => a = 1, b = 1, c = 1.

Kết quả: Số ước số của 30 là (1 + 1)(1 + 1)(1 + 1) = 8

Dạng 4: Chứng minh một số là hợp số

Ví dụ: Chứng minh rằng 123456789 là hợp số.

Lời giải:

• Tìm một ước số khác 1 và chính nó của số cần chứng minh. Số cần chứng minh là hợp số.

• 123456789 chia hết cho 3.

Kết quả: 123456789 là hợp số.

Dạng 5: Giải bài toán ứng dụng liên quan đến hợp số

Ví dụ: Một lớp học có 30 học sinh. Hỏi có bao nhiêu cách chia tổ sao cho số học sinh trong mỗi tổ là một hợp số?

Lời giải:

• Liệt kê các hợp số bé hơn hoặc bằng 30: 2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 24, 25, 30.

• Có 19 hợp số trong danh sách.

• Mỗi cách chia tổ là một tập hợp con của tập hợp 19 hợp số này.

• Số cách chia tổ là số tập con của tập hợp 19 hợp số.

• Theo công thức số tập con, số cách chia tổ là: 2¹⁹ = 524.288

Kết quả: Có 524.288 cách chia tổ sao cho số học sinh trong mỗi tổ là một hợp số.