Trực tâm là gì? Tính chất, cách xác định trực tâm trong tam giác (chính xác nhất)

Trực tâm là gì? Tính chất, cách xác định và công thức tính trực tâm

I. Trực tâm là gì?

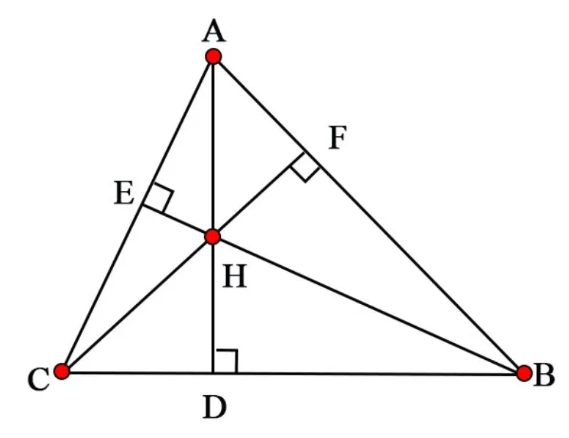
Trực tâm là giao điểm của ba đường cao tam giác, giữ một vị trí quan trọng trong hệ thống các điểm đặc biệt, bao gồm trọng tâm, tâm đường tròn ngoại tiếp và nội tiếp.

Mỗi đường cao là đoạn thẳng vuông góc với một cạnh và kéo dài từ đỉnh đối diện. Điểm trực tâm có những tính chất rất đặc biệt và quan trọng trong hình học, đặc biệt là trong việc nghiên cứu các tam giác nhọn, vuông, và tù.

Trực tâm của tam giác có một số tính chất đáng chú ý. Ví dụ, trong tam giác cân, trực tâm cũng là tâm của đường tròn nội tiếp và là trung điểm của cạnh đáy. Trong tam giác vuông, trực tâm nằm trên cạnh huyền và chính giữa hai đỉnh vuông góc. Trực tâm của tam giác cũng có tính chất là điểm duy nhất trong tam giác mà tổng khoảng cách từ trực tâm đến các đỉnh là nhỏ nhất. Trực tâm của tam giác không chỉ có ý nghĩa hình học mà còn được áp dụng trong các bài toán và bằng chứng liên quan đến tam giác. Hiểu rõ về trực tâm giúp chúng ta nắm bắt và áp dụng các tính chất của tam giác một cách hiệu quả trong giải toán và nghiên cứu hình học.

II. Cách xác định trực tâm trong tam giác

1. Xác định trực tâm trong tam giác nhọn

• Bước 1: Bắt đầu bằng cách vẽ tam giác nhọn bất kỳ. Một tam giác nhọn sẽ có cả ba góc đều nhỏ hơn 90 độ.

• Bước 2: Từ mỗi đỉnh của tam giác, kẻ một đường cao xuống cạnh đối diện (đường thẳng vuông góc với cạnh và kéo dài từ đỉnh đối diện).

• Bước 3: Điểm giao của ba đường vừa vẽ chính là trực tâm của tam giác nhọn. Trực tâm của tam giác nhọn nằm bên trong hình.

2. Xác định trực tâm trong tam giác vuông

• Bước 1: Vẽ một tam giác vuông với một góc 90 độ. Đây là một tam giác trong đó một góc vuông và hai góc nhọn còn lại.

• Bước 2: Trong tam giác vuông, trực tâm chính là đỉnh của góc vuông. Điều này có nghĩa là bạn không cần phải vẽ các đường vuông góc để tìm trực tâm, vì nó luôn trùng với đỉnh góc vuông.

• Bước 3: Để đảm bảo tính chính xác, có thể vẽ thêm đường cao từ đỉnh còn lại. Các đường này sẽ cắt nhau tại đỉnh góc vuông, xác nhận rằng đó chính là trực tâm.

3. Xác định trực tâm trong tam giác tù

• Bước 1: Vẽ một tam giác tù, trong đó một trong ba góc lớn hơn 90 độ.

• Bước 2: Kẻ các đường vuông góc từ mỗi đỉnh xuống cạnh đối diện, nhưng lưu ý rằng trong tam giác tù, các đường này có thể kéo dài ra bên ngoài tam giác.

• Bước 3: Do góc tù, ba đường cao sẽ "vươn ra" bên ngoài, giao nhau tại một điểm nằm ngoài hình, và điểm đó chính là trực tâm.

III. Tính chất của trực tâm tam giác

• Trực tâm là điểm trùng điểm giao của ba đường thẳng đồng trung và đồng quy trong tam giác, bao gồm:

+ Đường trung trực: Đường thẳng đi qua trực tâm và đỉnh tương ứng của cạnh.

+ Đường phân giác: Đường thẳng chia một góc trong tam giác thành hai phần bằng nhau, kết hợp với trực tâm.

+ Đường cao: Đường thẳng từ một đỉnh của tam giác vuông góc với cạnh đối diện, cắt nhau tại trực tâm.

• Trực tâm cắt đường trung trực của hai cạnh thành hai đoạn có độ dài bằng nhau. Điều này có nghĩa là trực tâm cách các đỉnh của tam giác một khoảng bằng nhau.

• Trực tâm là tâm của đường tròn ngoại tiếp của tam giác, nghĩa là nếu ta vẽ một đường tròn đi qua ba đỉnh của tam giác, trực tâm sẽ nằm trên đường tròn đó và là tâm của nó.

• Trực tâm của tam giác nhọn nằm bên trong tam giác, trong khi trực tâm của tam giác tù nằm bên ngoài tam giác.

• Trực tâm của tam giác vuông nằm trên cạnh huyền và chính giữa hai đỉnh vuông góc của tam giác.

• Trực tâm là điểm duy nhất trong tam giác mà nếu ta vẽ các đường từ trực tâm đến các đỉnh của tam giác, tổng độ dài các đường đó là nhỏ nhất. Điều này có nghĩa là trực tâm nằm gần nhất với các đỉnh của tam giác so với bất kỳ điểm nào khác.

• Trực tâm cũng là tâm của đường tròn ngoại tiếp của tam giác, tức là đường tròn lớn nhất mà có thể vẽ được qua ba đỉnh của tam giác.

• Vị trí phụ thuộc vào loại tam giác: Trực tâm có thể nằm trong, trên cạnh hoặc ngoài, tuỳ thuộc vào loại tam giác là nhọn, vuông hay tù. Trực tâm nằm bên trong hình nhọn, trùng với đỉnh góc vuông của hình vuông và bên ngoài hình tù.

• Quan hệ đối với tam giác vuông: Riêng với tam giác vuông, trực tâm có vị trí đặc biệt: chính là đỉnh góc vuông. Đây là một tính chất đặc biệt và có thể giúp giải nhanh các bài toán liên quan.

• Tính đồng phẳng: Trực tâm, tâm đường tròn ngoại tiếp, trọng tâm và tâm đường tròn nội tiếp của một tam giác đồng phẳng với nhau.

IV. Công thức tính trực tâm của tam giác

Để tính được toạ độ trực tâm là gì một cách chính xác, bạn có thể sử dụng phương pháp tính toán thông qua các tọa độ đỉnh tam giác. Giả sử tam giác có tọa độ ba đỉnh A, B, C và trực tâm là H. Có thể tính như sau:

• Xác định tọa độ của các đỉnh: Gọi tọa độ của ba đỉnh là A(x₁, y₁), B(x₂, y₂), và C(x₃, y₃) và trực tâm H(x_H,y_H)

• Xác định tọa độ x_H:

x_H = $\frac{x_1+x_2+x_3}{3}$

• Xác định tọa độ y_H:

y_H = $\frac{y_1+y_2+y_3}{3}$

V. Vai trò, ứng dụng của trực tâm

1.Vai trò của trực tâm

Trực tâm là một điểm quan trọng trong hình học, và có nhiều ứng dụng trong lĩnh vực này. Một trong những ứng dụng quan trọng nhất của trực tâm là tính toán diện tích của tam giác. Diện tích của tam giác bằng một nửa tích số độ dài đáy và chiều cao tương ứng với đáy đó. Giao điểm đường cao làm tâm của đường tròn nội tiếp của tam giác, chiều cao tương ứng với đáy đó chính là khoảng cách từ trực tâm đến đáy.

2. Ứng dụng của trực tâm trong hình học

Trực tâm trong tam giác có nhiều ứng dụng quan trọng và hữu ích trong lĩnh vực hình học và các ngành khoa học khác. Dưới đây là một số ứng dụng của trực tâm trong tam giác:

- Trực tâm là tâm trong đường tròn ngoại tiếp tam giác: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Trực tâm là tâm của đường tròn ngoại tiếp, nghĩa là khoảng cách từ trực tâm đến mỗi đỉnh của tam giác là bằng nhau.

- Trực tâm là tâm trong đường tròn nội tiếp tam giác: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với các cạnh của tam giác. Trực tâm là tâm của đường tròn nội tiếp, nghĩa là các đoạn thẳng nối từ trực tâm đến các điểm tiếp xúc cạnh là vuông góc với cạnh tương ứng.

- Trực tâm là tâm trong đường tròn nội tiếp nửa ngoại tiếp tam giác: Đường tròn nội tiếp nửa ngoại tiếp tam giác là đường tròn tiếp xúc với một cạnh và tiếp xúc tiếp với phần còn lại của cạnh kế tiếp. Trực tâm là tâm của đường tròn nội tiếp nửa ngoại tiếp.

- Trực tâm là trung điểm của các đoạn thẳng nối từ trực tâm đến các đỉnh của tam giác: Điều này có nghĩa là trực tâm chia đôi các đoạn thẳng nối từ trực tâm đến các đỉnh của tam giác.

- Trực tâm là giao điểm của ba đường cao của tam giác: Đường cao là đoạn thẳng vuông góc với cạnh tương ứng và đi qua đỉnh không nằm trên cạnh đó. Trực tâm là điểm giao của ba đường cao của tam giác.

- Trực tâm giúp xác định các thuộc tính và vị trí của tam giác: Nhờ trực tâm, ta có thể dễ dàng xác định được tâm của đường tròn ngoại tiếp, đường tròn nội tiếp, tính chất đối xứng và cân của tam giác.

- Trực tâm có thể được sử dụng để tính toán các giá trị hình học khác như diện tích tam giác, khoảng cách từ trực tâm đến các điểm khác trong tam giác, và các thuộc tính khác của tam giác.

=> Tóm lại, trực tâm là một điểm quan trọng và có nhiều ứng dụng trong tam giác. Việc hiểu và sử dụng trực tâm giúp ta nắm bắt và áp dụng các tính chất và quy luật hình học trong tam giác một cách hiệu quả.

3. Ứng dụng của trực tâm trong thực tế

• Kiến trúc và xây dựng

Việc có trụ cột đặt tại vị trí được xác định thông qua trực tâm giúp tăng khả năng chịu tải của công trình. Trọng lực từ các phần trên cao của công trình được truyền xuống đáng kể thông qua trụ cột hỗ trợ. Và việc đặt chúng tại vị trí chiến lược giúp giảm nguy cơ đổ sập.

• Quy hoạch đô thị

Trực tâm có thể được sử dụng để xác định trung tâm của khu vực cộng đồng hoặc thành phố, và từ đó, quy hoạch viên có thể đưa ra quyết định về vị trí lắp đặt các trạm phục vụ như bệnh viện, trường học, công viên, hay các cơ sở công cộng khác. Việc tập trung các dịch vụ này quanh một trực tâm có thể giúp tối ưu hóa tiện ích và thuận tiện cho cư dân địa phương.

Quy hoạch đô thị có sự tích hợp giữa giao điểm này có thể góp phần vào việc xây dựng thành phố thông minh. Các dữ liệu vị trí được thu thập từ trực tâm có thể được kết hợp với công nghệ thông tin để cải thiện quản lý giao thông, dịch vụ công cộng và an ninh, tạo ra một môi trường sống hiệu quả và tiện nghi.

• Nghiên cứu đất đai

Trong lĩnh vực nghiên cứu đất đai, việc xác định trực tâm có thể được thực hiện thông qua các phương pháp đo lường chính xác. Như toàn bộ GPS (Global Positioning System), thiết bị định vị vệ tinh,… Hoặc các kỹ thuật đo lường địa lý chính xác khác. Một khi đã được xác định được, các trạm đo đất đai sẽ được đặt xung quanh điểm này để đảm bảo rằng các dữ liệu thu thập được là đại diện cho toàn bộ khu vực quan tâm.

• Hệ thống điều khiển Robot

Thường được tích hợp với hệ thống đo lường, như các cảm biến vị trí, hệ thống GPS, hoặc các thiết bị đo lường vị trí vệ tinh khác. Điều này giúp xác định một cách chính xác vị trí tuyệt đối của robot trong không gian toàn cầu. Các đoạn thẳng nối tâm này với các đỉnh của tam giác cung cấp một cơ sở hình học mạnh mẽ để xác định vị trí tương đối của robot trong môi trường cụ thể.

• Giáo dục hình học

Giao điểm đường cao là một ví dụ thực tế giáo dục trong việc giảng dạy hình học. Nó giúp học sinh hiểu rõ hơn về các đặc tính và tính chất. Từ đó phát triển kỹ năng giải quyết vấn đề và tư duy hình học.

• Ứng dụng trong công nghiệp và công nghệ

Trong môi trường công nghiệp, quy trình giám sát từ xa đóng vai trò quan trọng để đảm bảo an toàn và hiệu suất. Sử dụng trực tâm giúp xác định vị trí của các thiết bị và nhân viên. Đồng thời cung cấp dữ liệu chính xác cho các hệ thống giám sát từ xa. Điều này có thể áp dụng trong các nhà máy sản xuất, khu vực lưu kho, và các môi trường công nghiệp khác.

VI. Bài tập về trực tâm trong tam giác

Bài 1. Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC.

Giải:

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC, BH ⊥ AC, CH ⊥ AB

Trong ΔAHB, ta có:

AC ⊥ BH

BC ⊥ AH

Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

AB ⊥ CH

CB ⊥ AH

Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

BA ⊥ HC

CA ⊥ BH

Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

Bài 2. Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.

Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.

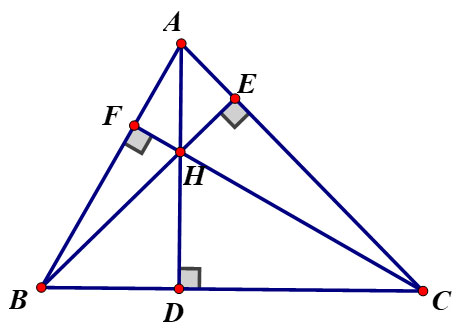
Giải:

Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.

⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.

ΔHBC có :

AD ⊥ BC nên AD là đường cao từ H đến BC.

BA ⊥ HC tại F nên BA là đường cao từ B đến HC

CA ⊥ BH tại E nên CA là đường cao từ C đến HB.

AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.

Bài 3. Cho △ABC có các đường cao AD; BE; CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.

a) Chứng minh: JT⊥EFJT⊥EF

b) Chứng minh: IE⊥JEIE⊥JE

c) Chứng minh: DA là tia phân giác của góc EDF.

d) Gọi P; Q là hai điểm đối xứng của D qua AB và AC

Chứng minh: P; F; E; Q thẳng hàng.

Bài 4. Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).

Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.

Chứng minh KN ⊥ IM.