200 bài tập hệ thức lượng nâng cao (2024) có đáp án

200 bài tập hệ thức lượng nâng cao (2024) có đáp án

I. Lý thuyết

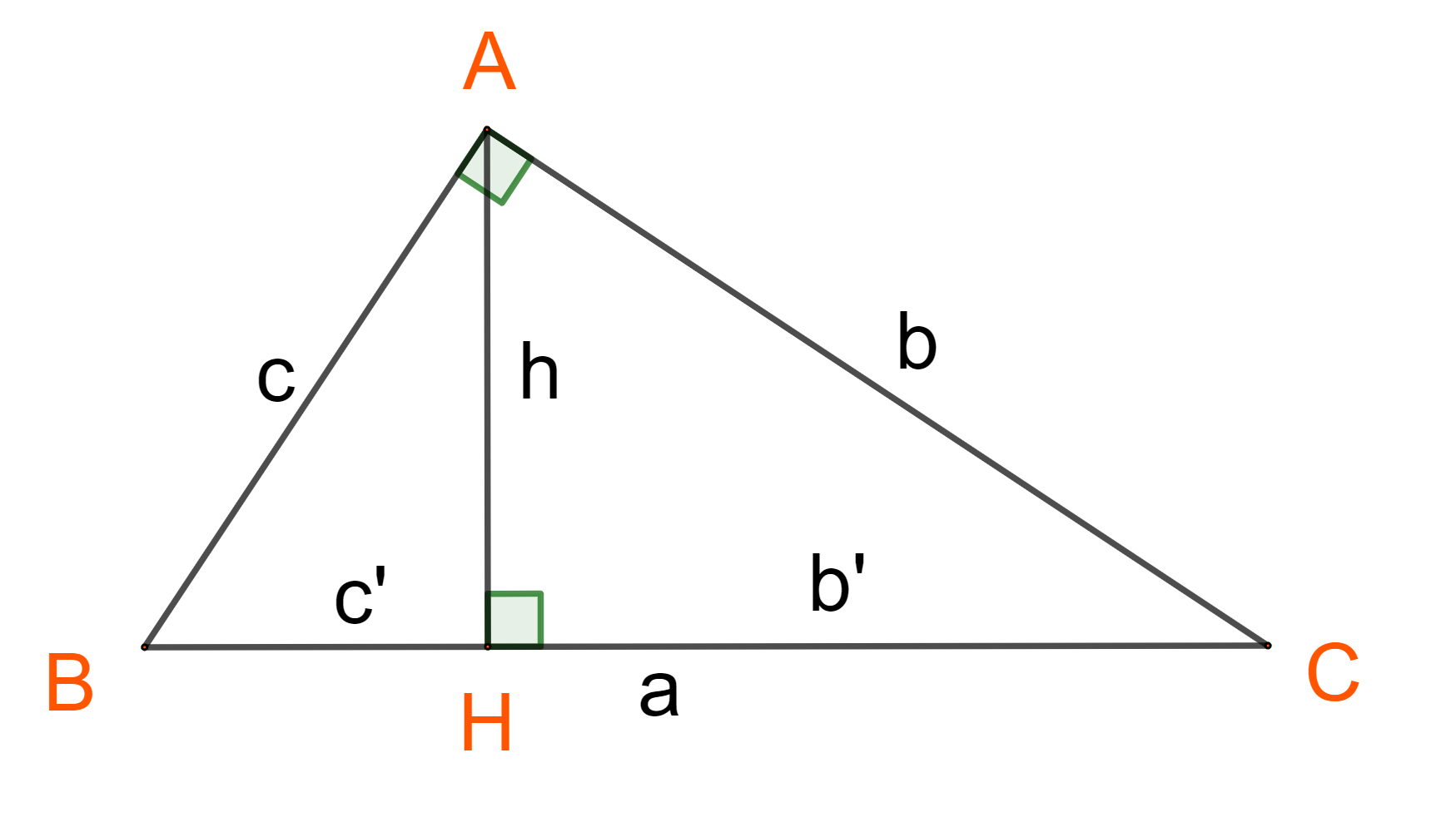
Cho tam giác $ABC$ vuông góc tại đỉnh $A$ ($\hat{A}={90}^0$), ta có:

1. $b^2=a{b}^{\prime };c^2=a.c^{\prime }$

2. Định lý Pitago : $a^2=b^2+c^2$

3. $a.h=b.c$

4. $h^2=b^{\prime }.c^{\prime }$

5. ${\displaystyle \frac{1}{h^2}}$ = ${\displaystyle \frac{1}{b^2}}$ + ${\displaystyle \frac{1}{c^2}}$

1. Định lý cosin

Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với $cosin$ của góc xen giữa chúng.

Ta có các hệ thức sau:

$$\begin{array}{rl}& a^2=b^2+c^2-2bc.\cos A(1)\\ & b^2=a^2+c^2-2ac.\cos B(2)\\ & c^2=a^2+b^2-2ab.\cos C(3)\end{array}$$

Hệ quả của định lí cosin:

$\cos A={\displaystyle \frac{b^2+c^2-a^2}{2bc}}$

$\cos B={\displaystyle \frac{a^2+c^2-b^2}{2ac}}$

$\cos C={\displaystyle \frac{a^2+b^2-c^2}{2ab}}$

Áp dụng: Tính độ dài đường trung tuyến của tam giác:

Cho tam giác $ABC$ có các cạnh $BC=a,CA=b$ và $AB=c$. Gọi $m_a,m_b$ và $m_c$ là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh $A,B,C$ của tam giác. Ta có

${m_a}^2$ = ${\displaystyle \frac{2.(b^2+c^2)-a^2}{4}}$

${m_b}^2$ = ${\displaystyle \frac{2.(a^2+c^2)-b^2}{4}}$

${m_c}^2$ = ${\displaystyle \frac{2.(a^2+b^2)-c^2}{4}}$

2. Định lí sin

Định lí: Trong tam giác $ABC$ bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là

${\displaystyle \frac{a}{\sin A}}={\displaystyle \frac{b}{\sin B}}={\displaystyle \frac{c}{\sin C}}=2R$

với $R$ là bán kính đường tròn ngoại tiếp tam giác

Công thức tính diện tích tam giác

Diện tích $S$ của tam giác $ABC$ được tính theo một trong các công thức sau

$S={\displaystyle \frac{1}{2}}ab\sin C={\displaystyle \frac{1}{2}}bc\sin A$ $={\displaystyle \frac{1}{2}}ca\sin B(1)$

$S={\displaystyle \frac{abc}{4R}}(2)$

$S=pr(3)$

$S=\sqrt{p(p-a)(p-b)(p-c)}$ (công thức Hê - rông) $(4)$

Trong đó:$BC=a,CA=b$ và $AB=c$; $R,r$ là bán kính đường tròn ngoại tiếp, bk đường tròn nội tiếp và $S$ là diện tích tam giác đó.

3. Giải tam giác và ứng dụng vào việc đo đạc

Giải tam giác : Giải tam giác là đi tìm các yếu tố (góc, cạnh) chưa biết của tam giác khi đã biết một số yếu tố của tam giác đó.

Muốn giải tam giác ta cần tìm mối liên hệ giữa các góc, cạnh đã cho với các góc, các cạnh chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.

Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:

a) Giải tam giác khi biết một cạnh và hai góc.

=> Dùng định lí sin để tính cạnh còn lại.

b) Giải tam giác khi biết hai cạnh và góc xen giữa

=> Dùng định lí cosin để tính cạnh thứ ba.

Sau đó dùng hệ quả của định lí cosin để tính góc.

c) Giải tam giác khi biết ba cạnh

Đối với bài toán này ta sử dụng hệ quả của định lí cosin để tính góc:

$\cos A={\displaystyle \frac{b^2+c^2-a^2}{2bc}}$

$\cos B={\displaystyle \frac{a^2+c^2-b^2}{2ac}}$

$cosC={\displaystyle \frac{a^2+b^2-c^2}{2ab}}$

Chú ý:

1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)

2. Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.

II. Bài tập vận dụng

Bài 1: Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.

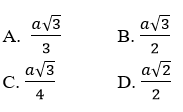
Đáp án A

Bài 2: Cho tam giác ABC có AB = 10, AC = 12, góc A = 150o.Diện tích của tam giác ABC bằng

A. 60 B. 30 C.60√3 D. 30√3

Đáp án B

Bài 3: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng

A. 4 B. 3 C. 2 D. 1

Đáp án D

Bài 4: Cho tam giác ABC có AC = 6, BC = 8. h_a,h_blần lượt là độ dài các đường cao đi qua các đỉnh A, B. Tỉ số h_a/h_bbằng

Đáp án A

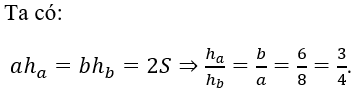
Bài 5: Cho tam giác ABC có a = 5, b = 6, c = 7. Diện tích của tam giác ABC bằng

A. 12√6 B. 3√6 C. 6√6 D. 9√6

Đáp án C

Bài 6: Cho tam giác ABC có a = 3, b = 5, c = 6. Bán kính đường trong nội tiếp của tam giác bằng

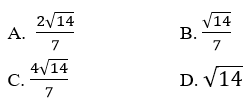
Đáp án A

Bài 7: Cho tam giác ABC có a² =b² + c² - bc. Số đo của góc A là

A. 135^o B. 150^o C. 60^o D. 120^o

Đáp án C

Ta có: a² = b² + c² – bc nên b² + c² – a² = bc

Áp dụng hệ quả định lí cosin trong tam giác ta có:

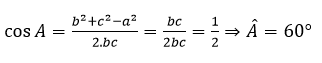
Bài 8: Cho tam giác ABC có a² =b² + c² + √2.bc. Số đo của góc A là

A. 135^o B. 45^o C. 120^o D. 150^o

^{Đáp án A}

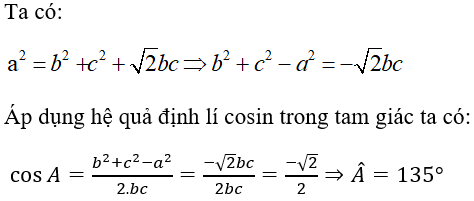
Bài 9: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

A. Nếu b² +c² > a² thì góc A > 90^o

B. Nếu b² +c² = a² thì góc A ≠ 90^o

^{C. Nếu b2 +c2 ≠ a2 thì tam giác ABC không phải là tam giác vuông}

^{D. Nếu b2 +c2 > a2 thì góc A > 90o}

^{Đáp án D}

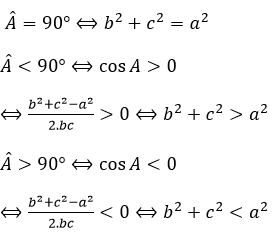
^{Bài 10: Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là}

A. Tam giác nhọn

B. Tam giác tù

C. Tam giác vuông

D. Tam giác đều

Đáp án C

Ta có: a² + b² = c² nên tam giác ABC là tam giác vuông.

^{Bài 11:Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là}

A. Tam giác nhọn

B. Tam giác tù

C. Tam giác vuông

D. Tam giác đều

Đáp án A

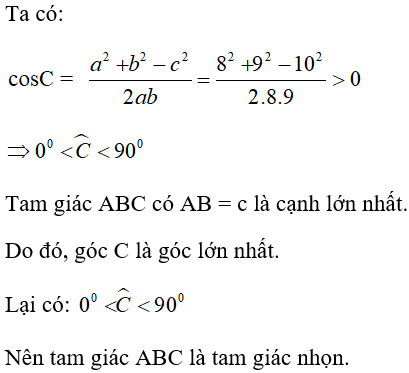
Bài 12: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

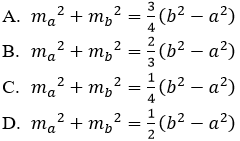
Đáp án A

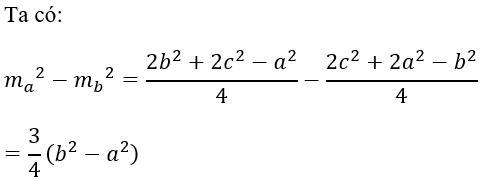
Bài 13: Cho tam giác ABC trọng tâm G. Bình phương độ dài đoạn thẳng GA bằng

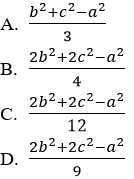
Đáp án D

Bài 14: Cho tam giác ABC thỏa mãn c = a.cos B. Khẳng định nào sau đây là đúng?

A. Tam giác ABC là tam giác cân

B. Tam giác ABC là tam giác nhọn

C. Tam giác ABC là tam giác vuông

D. Tam giác ABC là tam giác tù

Đáp án C

Bài 15: Cho tam giác ABC có a = 30, góc = 60^o. Khẳng định nào sau đây là đúng?

A. R = 10√3 B. R = 20√3 C. R = 10 D. R = 20

Đáp án A

Bài 16: Cho tam giác ABC có a = 10 cm, h_a= 3 cm. Diện tích của tam giác ABC là

A. 30 (cm)² B. 15 (cm)² C. 60 (cm)² D. 7,5 (cm)²

^{Đáp án A}

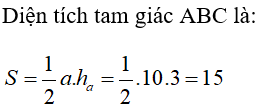
^{Bài 17: Cho tam giác ABC có AB = 4, AC =6, BC = 8. Diện tích của tam giác ABC là}

^{A. 3√15 B. 6√15 C. (3√15)/2 D. √15}

^{Đáp án A}

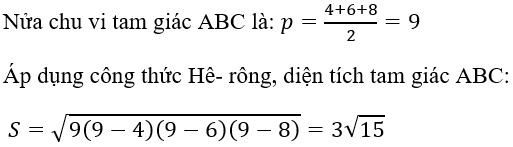
Bài 18: Đáp án nào sau đây phù hợp với diện tích của hình lục giác ở hình bên?

A. 12 + 8√3

B. 24 + 16√3

C. 24 + 4√3

D. 24 + 8√3

Đáp án D

Hình lục giác đã cho là hợp của 2 tam giác đều có độ dài cạnh là 4 và 1 hình chữ nhật với độ dài 2 cạnh là 4 và 6.

Bài 19: Bề mặt viên gạch hình lục lăng có dạng hình lục giác đều cạnh 8 cm. Diện tích bề mặt của viên gạch là

A. 96 (cm)² C. 96√3 (cm)²

B. 16√3 (cm)² D. 48√3 (cm)²

Đáp án C

Gọi O là tâm của hình lục giác đều – O là giao điểm các đường chéo.

Hình lục giác đều cạnh 8 cm được chia thành sau tam giác đều cạnh 8 cm.

Diện tích mỗi tam giác đều là:

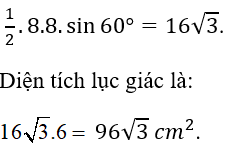
Bài 20: Tam giác cân cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là

A. a²cos⁡α/2

B. a²sin⁡α/2

C. a²cos⁡α

D. a²sin⁡α

Đáp án B

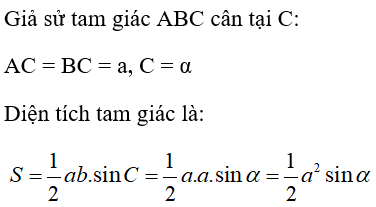
Bài 21: Đa giác đều n đỉnh và nội tiếp đường tròn bán kính R có diện tích là

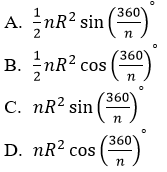
Đáp án A

Bài 22: Đáp án nào sau đây phù hợp với diện tích của phần được tô ở hình bên?

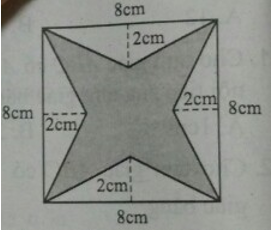
A. 48 (cm)²

B. 32 (cm)²

C. 40 (cm)²

D. 56 (cm)²

Đáp án B

^{Diện tích phần được tô màu bằng hiệu diện tích của hình vuông cạnh 8cm và 4 tam giác bằng nhau có 1 cạnh bằng 8 và đường cao ứng với cạnh đó bằng 2 cm. Diện tích của 1 tam giác là: S = (1/2).2.8 = 8 Diện tích hình vuông là: S’ = 82 = 64 Diện tích phần tô đậm là: 64 – 4.8 = 32.}