50 bài tập sắp xếp chỗ ngồi và đồ vật (có đáp án 2025) và cách giải
Với tài liệu về 50 bài tập sắp xếp chỗ ngồi và đồ vật có đáp án bao gồm: lý thuyết và bài tập cũng như những định nghĩa, tính chất, các dạng bài sẽ giúp bạn nắm vững kiến thức và học tốt môn Toán hơn.
50 bài tập sắp xếp chỗ ngồi và đồ vật
I. Lý thuyết
+ Xác định số đối tượng cần sắp xếp.
+ Xác định số vị trí để sắp xếp đối tượng.
+ Dùng hoán vị hoặc chỉnh hợp hoặc tổ hợp để tính số cách sắp xếp đó.
Lưu ý:
+ Nếu có đối tượng khác nhau xếp vào n(n≥k) vị trí thì có: Akn cách sắp xếp.
+ Nếu đối tượng giống nhau xếp vào n(n≥k) vị trí thì có: Ckn cách sắp xếp.
+ Một số bài toán chứa điều kiện thì có thể chia nhỏ thành các trường hợp để khi sắp xếp không bị lặp lại.
II. Bài tập vận dụng
Bài 1: Có bao nhiêu cách sắp xếp năm bạn học sinh A, B, C, D, E vào một chiếc ghế dài sao cho:
1. Bạn C ngồi chính giữa.
2. Hai bạn A và E ngồi ở hai đầu ghế.
Lời giải:
1. Xếp C ngồi chính giữa có một cách xếp.
Xếp 4 học sinh A, B, D, E vào 4 vị trí còn lại có 4! cách xếp.
Vậy có: 4!=24 cách xếp.
2. Xếp A và E ngồi ở hai đầu ghế có 2 cách xếp là A ngồi đầu này, E ngồi đầu kia của ghế và ngược lại.
Xếp 3 học sinh B, C, D vào 3 vị trí còn lại có 3! cách xếp có 2.3!=12 cách xếp.
Bài 2: Một nhóm gồm 10 học sinh, trong đó có 7 nam và 3 nữ. Hỏi có bao nhiêu cách sắp xếp 10 học sinh trên thành một hàng dài sao cho 7 học sinh nam phải đứng liền nhau.
Lời giải:
Coi 7 học sinh nam đứng liền nhau như một vị trí, đặt a là vị trí của 7 học sinh nam thì số cách để bố trí a đứng liền nhau xen kẽ với 3 học sinh nữ bằng 4!. Nhưng để xếp 7 học sinh nam đứng liền nhau thì lại có 7! cách.
Vậy tất cả có: 4!7!=120960 cách.
Bài 3: Có 12 đội bóng tham gia tranh giải vô địch quốc gia. Trong vòng đấu loại các đối thủ đấu với nhau theo thể thức vòng tròn, hai đội bóng bất kỳ gặp nhau hai trận, một trận lượt đi và một trận lượt về. Hỏi có bao nhiêu trận đấu trong vòng loại?
Lời giải:
Mỗi đội bóng bất kỳ thì 11 trận đấu với 11 đội bóng còn lại.
Suy ra số trận đấu là: 12.11=132 trận.
Bài 4: Có bao nhiêu cách chọn 4 cầu thủ khác nhau trong 10 cầu thủ của đội bóng quần vợt để chơi bốn trận đấu đơn, các trận đấu là có thứ tự?
Lời giải
Mỗi cách chọn bốn cầu thủ của đội bóng là một chỉnh hợp chập 4 của 10 phần tử.
Ta có: A410=5040 cách chọn.
Bài 5. Có bao nhiêu cách sắp xếp chỗ ngồi cho 10 bạn trong đó có An và Bình vào 10 ghế kê thành hàng ngang sao cho
a) Hai bạn An và Bình ngồi cạnh nhau
b) Hai bạn An và Bình không ngồi cạnh nhau
Lời giải
a) Hai bạn An và Bình ngồi cạnh nhau
Ghép 2 bạn An và Bình ngồi gần nhau: Số cách sắp xếp của 2 bạn 2!
An, Bình và 8 bạn còn lại được tính là 9 phần tử: 9!
Số cách thực hiện là: 2!.9!
b) Hai bạn An và Bình không ngồi cạnh nhau
Sắp xếp chỗ ngồi cho 10 bạn bất kì là: 10!
Số cách sắp xếp chỗ để An và Bình không ngồi cạnh nhau là : 10! – 9!.2! = 8.9!
Bài 6. Một học sinh có 12 cuốn sách đôi một khác nhau, trong đó có 2 cuốn sách Toán, 4 cuốn sách Văn và 6 cuốn sách Anh. Hỏi có bao nhiêu cách xếp tất cả các cuốn sách lên một kệ sách dài, nếu các cuốn sách cùng môn được xếp kề nhau?
Lời giải:
Có 3! cách xếp 3 nhóm sách (nhóm sách Toán, nhóm sách Văn, nhóm sách Anh) lên một kệ dài.
Mỗi cách xếp đó có 2! cách xếp 2 cuốn sách toán, 4! cách xếp 4 cuốn sách Văn và 6! cách xếp cuốn sách Anh.
Vậy theo quy tắc nhân có: 3!.2!.4!.6!=207360 cách xếp tất cả các cuốn sách lên một kệ sách dài, và các cuốn sách cùng môn được xếp kề nhau.
Bài 7. Một bàn dài có hai dãy ghế đối diện nhau, mỗi dãy có 6 ghế. Người ta muốn xếp chỗ ngồi cho 6 học sinh trường A và 6 học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách xếp trong mỗi trường hợp sau:
1. Bất cứ 2 học sinh nào ngồi cạnh nhau hoặc đối diện nhau thì khác trường với nhau.
2. Bất cứ 2 học sinh nào ngồi đối diện nhau thì khác trường với nhau.
Lời giải:
1) Có hai sơ đồ xếp chỗ ngồi sao cho cứ 2 học sinh nào ngồi cạnh nhau hoặc đối diện nhau thì khác trường với nhau là:
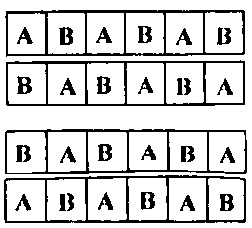
Mỗi sơ đồ có 6! cách sắp xếp 6 học sinh trường A và 6! cách sắp xếp 6 học sinh trường B.
Vậy theo quy tắc nhân có: 2.6!.6!=1036800 cách sắp xếp.
2) Học sinh thứ nhất trường A ngồi trước: có 12 cách chọn ghế để ngồi.
Sau đó, chọn học sinh trường B ngồi đối diện với học sinh thứ nhất trường A: có 6 cách chọn học sinh trường B.
Học sinh thứ hai của trường A còn 10 chỗ để chọn, chọn học sinh trường B ngồi đối diện với học sinh thứ hai trường A: có 5 cách chọn ..v.v..
Vậy có 12.6.10.5.8.4.6.3.4.2.2.1 =26.6!.6!=33177600 cách.
Bài 8. Có 5 thẻ trắng và 5 thẻ đen, đánh dấu mỗi loại theo các số 1, 2, 3, 4, 5. Có bao nhiêu cách sắp xếp tất cả các thẻ này thành một hàng sao cho hai thẻ cùng màu không nằm liền nhau.
Lời giải:
Có 2 trường hợp xảy ra:
Trường hợp 1: Các thẻ trắng ở vị trí lẻ, các thẻ đen ở vị trí chẵn.
Có 5! cách sắp xếp 5 thẻ trắng và 5! cách sắp xếp 5 thẻ đen.
Suy ra có: 5!.5! cách sắp xếp.
Trường hợp 2: Các thẻ trắng ở vị trí chẵn, các thẻ đen ở vị trí lẻ.
Có 5! cách sắp xếp 5 thẻ trắng và 5! cách sắp xếp 5 thẻ đen.
Suy ra có 5!.5! cách sắp xếp.
Vậy có: 5!.5!+5!.5!=28800 cách sắp xếp.
Bài 9. Một thầy giáo có 12 cuốn sách đôi một khác nhau trong đó có 5 cuốn sách Văn, 4 cuốn sách Nhạc và 3 cuốn sách Họa. Ông muốn lấy ra 6 cuốn và tặng cho 6 học sinh A, B, C, D, E, F mỗi em một cuốn.
1. Giả sử thầy giáo chỉ muốn tặng cho các học sinh trên những cuốn sách thuộc 2 thể loại Văn và Nhạc. Hỏi có bao nhiêu cách tặng?
2. Giả sử thầy giáo muốn rằng sau khi tặng sách xong, mỗi một trong ba loại sách trên đều còn lại ít nhất một cuốn. Hỏi có bao nhiêu cách chọn?
Lời giải:
1. Số cách tặng là số cách chọn 6 cuốn sách từ 9 cuốn có kể thứ tự, tức là mỗi cách chọn là một chỉnh hợp chập 6 của 9.
Vậy số cách tặng là A69=60480.
2. Nhận xét: không thể chọn sao cho cùng hết 2 loại sách.
Số cách chọn 6 cuốn sách từ 12 cuốn sách là: A612=66528.
Số cách chọn sao cho không còn sách Văn là: A55.A17=840.
Số cách chọn sao cho không còn sách Nhạc là: A44.A28=1344.
Số cách chọn sao cho không còn sách Hoạ là: A33.A39=3024.
Số cách chọn cần tìm là: 66528–
Bài 10. Có nam và nữ ngồi vào hai dãy ghế đối diện nhau, mỗi dãy có ghế. Hỏi:
a) Có bao nhiêu cách sắp xếp sao cho hai người đối diện khác phái?
b) Có bao nhiêu cách sắp xếp mà nam nữ ngồi xen kẽ và đối diện?
Lời giải:
a) Học sinh nam thứ nhất có cách chọn chỗ ngồi, sau đó chọn học sinh nữ ngồi đối diện với học sinh nam đã chọn có cách.
Học sinh nam thứ hai có cách chọn chỗ ngồi, chọn học sinh nữ ngồi đối diện có cách.
Học sinh nam thứ ba có cách chọn chỗ ngồi, chọn học sinh nữ ngồi đối diện có cách.
Học sinh nam thứ tư có cách chọn chỗ ngồi, chọn học sinh nữ ngồi đối diện có cách.
Học sinh nam thứ hai có cách chọn chỗ ngồi, chọn học sinh nữ ngồi đối diện có cách.
Vậy có cách sắp xếp để hai người đối diện khác phái.
Cách khác:
Chọn cặp nam, nữ thứ nhất và xếp vào ghế đối diện đã chọn có cách chọn (có thể nam_nữ hoặc nữ_nam).
Chọn cặp nam, nữ thứ hai và xếp vào ghế đối diện đã chọn có cách chọn (có thể nam_nữ hoặc nữ_nam).
Chọn cặp nam, nữ thứ ba và xếp vào ghế đối diện đã chọn có cách chọn (có thể nam_nữ hoặc nữ_nam).
Chọn cặp nam, nữ thứ tư và xếp vào ghế đối diện đã chọn có cách chọn (có thể nam_nữ hoặc nữ_nam).
Chọn cặp nam, nữ thứ năm và xếp vào ghế đối diện đã chọn có cách chọn (có thể nam_nữ hoặc nữ_nam).
Vậy có cách.
b) Có sơ đồ để sắp xếp nam nữ đối diện và xen kẽ là: (ký hiệu B: nam và G: nữ).
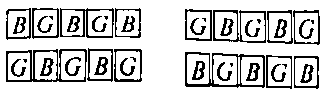
Mỗi sơ đồ có cách sắp xếp nam và cách sắp xếp nữ.
Vậy có cách sắp xếp nam nữ ngồi xen kẽ và đối diện.
Bài 11: Cần xếp nam và nữ vào hàng ghế có chỗ ngồi sao cho nam ngồi kề nhau và nữ ngồi kề nhau. Hỏi có bao nhiêu cách.
Lời giải:
Giả sử ghế có chỗ ngồi như sau: ▯▯▯▯▯▯▯.
Đầu tiên ta coi nam là một khối thống nhất là a và nữ là một khối thống nhất là b và c là 2 ghế trống còn lại.
+ Hoán vị khối a, b và c có cách.
+ Có cách sắp xếp nam của khối a và cách xếp nữ của khối b
+ c gồm ghế không phân biệt nên chỉ có cách.
Vậy có cách sắp xếp.
Bài 12: Có bao nhiêu cách chọn cầu thủ khác nhau trong cầu thủ của đội bóng quần vợt để chơi bốn trận đấu đơn, các trận đấu là có thứ tự?
Lời giải:
Mỗi cách chọn bốn cầu thủ của đội bóng là một chỉnh hợp chập của phần tử.
Ta có: cách chọn.
Bài 12: Người ta xếp ngẫu nhiên lá phiếu từ đến cạnh nhau.
a) Có bao nhiêu cách sắp xếp để các phiếu số chẵn luôn ở cạnh nhau .
b) Có bao nhiêu cách xếp để các phiếu phân thành các nhóm chẵn lẻ riêng biệt.
Lời giải:
Giả sử lá phiếu chẵn đứng cạnh nhau là một khối thống nhất A
Xếp khối A và lá phiếu còn lại có cách xếp.
Xếp lá phiếu trong khối A có cách xếp.
Vậy có cách xếp.
b) Có trường hợp để xếp lá phiếu thành hai nhóm riêng biệt đó là các phiếu chẵn ở bên trái và
các phiếu lẻ ở phía bên phải và ngược lại.
Mỗi trường hợp có cách xếp phiếu lẻ và cách xếp phiếu chẵn.
Vậy có cách xếp.
Bài 13: Một tổ gồm nam và nữ. Có bao nhiêu cách xếp hàng sao cho các bạn nữ đứng thành 2 cặp và cặp này không đứng cạnh nhau?
Lời giải:
Chọn nhóm A gồm nữ là cách chọn.
nữ còn lại là nhóm B có cách chọn.
Suy ra có cách chia nữ thành nhóm A và B (mỗi nhóm nữ).
Mỗi cách chia trên có cách xếp nhóm A, B và bạn nam. Và có cách xếp nữ trong nhóm A, cách xếp nữ trong nhóm B.
Vậy có cách sắp xếp nam và nữ theo một hàng sao cho nữ đứng thành 2 cặp.
Mặt khác khi hoán đổi vị trí cho nhau thì số nữ sẽ được tính lặp lại lần do đó số cách sắp xếp là:
cách.
Trong các cách trên ta xét trường hợp nữ đứng cạnh nhau.
Gọi C là khối thống nhất của nữ đứng cạnh nhau.
Có cách xếp C và bạn nam.
Mỗi cách xếp như trên có cách xếp bạn nữ trong khối C.
Suy ra có: cách xếp để nữ đứng cạnh nhau.
Vậy có cách xếp thỏa mãn yêu cầu bài toán.
Cách khác:
Giả sử xếp nam và nữ thành hàng theo số thứ tự:
![]()
Ta tính số trường hợp xảy ra như sau:
+ Nếu nữ xếp vào vị trí thì nữ còn lại có cách chọn vị trí (; ; ; ; ; ; ).
+ Nếu nữ xếp vào vị trí thì nữ còn lại có cách xếp vào vị trí liền nhau mà không trùng với trường hợp trên.
+ Nếu nữ xếp vào vị trí thì nữ còn lại có cách xếp vào vị trí liền nhau mà không trùng trường hợp trên.
… … …
+ Nếu nữ xếp vào vị trí thì nữ còn lại có cách xếp vào vị trí
Suy ra có tất cả trường hợp để nữ xếp thành cặp và cặp này không đứng cạnh nhau.
Mỗi trường hợp có cách xếp nữ và cách xếp nam.
Vậy có cách xếp thỏa mãn yêu cầu bài toán.
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)
