Hệ số góc là gì? Cách tính hệ số góc và các dạng bài tập (có đáp án)

Hệ số góc là gì? Cách tính hệ số góc và các dạng bài tập (có đáp án)

1. Thế nào là hệ số góc

Hệ số góc là đại lượng thể hiện độ dốc của một đường thẳng nào đó so với trục Ox trong mặt phẳng tọa độ. Được ký hiệu là hệ số góc k, nó biểu hiện cho tỷ lệ thay đổi giữa tọa độ y và tọa độ x của các điểm trên đường thẳng.

Như vậy, hệ số góc của đường thẳng càng cao thì đường thẳng càng dốc. Về mặt ký hiệu, trong phương trình y = kx + b, hệ số góc k là hệ số đứng trước x và cho biết hướng của đường thẳng này trên mặt phẳng tọa độ.

2. Ý nghĩa của hệ số góc

Thể hiện độ dốc

Một trong những ý nghĩa quan trọng nếu bạn đang tìm hiểu hệ số góc là gì chính là khả năng thể hiện độ dốc của đường thẳng. Đường thẳng có hệ số góc k lớn sẽ có độ dốc cao hơn, trong khi k nhỏ thì trở nên ít dốc, gần như ngang hơn. Điều này rất hữu ích trong các ứng dụng thực tế, như xác định độ nghiêng của mặt đất trong địa chất hoặc tính toán độ dốc của đường trong xây dựng.

Cho thấy tốc độ thay đổi

Hệ số góc k cũng thể hiện tốc độ thay đổi giữa các biến x và y. Nếu k có giá trị lớn, y sẽ tăng hoặc giảm nhanh chóng khi x thay đổi. Ngược lại, k nhỏ biểu thị tốc độ thay đổi chậm. Trong kinh tế và khoa học, hệ số này là yếu tố giúp phân tích tốc độ tăng trưởng hoặc suy giảm của dữ liệu.

Thể hiện hướng của đường thẳng

Hệ số góc của đường thẳng cũng cho biết chiều hướng của nó đấy nhé. Trường hợp nếu k > 0, đường thẳng sẽ đi lên từ trái qua phải (hướng dương). Còn nếu k < 0, đường thẳng sẽ đi xuống từ trái qua phải (hướng âm). Trường hợp đặc biệt là khi hệ số góc bằng 0, đường thẳng sẽ song song với trục x, thể hiện không có độ dốc.

3. Công thức hệ số góc

Xét đường thẳng d có phương trình như sau: y = kx + b (k0).

Trong hệ trục toạ độ Oxy, là góc giữa trục Ox cùng đường thẳng d, các trường hợp xảy ra như sau:

• Khi α nhỏ hơn 90°, ta có k > 0 và k = tan α.

• Khi α lớn hơn 90°, ta có k < 0 và k =-tan (180°-α).

• Nếu hệ số góc k dương, α là góc nhọn và k càng lớn thì góc α càng tiến gần 90°.

• Nếu hệ số góc k âm, α là góc tù và k càng lớn (theo giá trị tuyệt đối) thì α càng tiến gần 180°.

Nếu không biết góc mà có hai điểm A(x₁, y₁) và B(x₂, y₂) nằm trên d, hệ số góc của đường thẳng có thể tính như sau:

k = $\frac{y_2-y_1}{x_2-x_1}$

Với công thức tính hệ số góc này, chỉ cần thay các giá trị x và y của hai điểm trên đường thẳng là có thể xác định k. Đây là một cách tính đơn giản nhưng rất hiệu quả, giúp tìm ra độ nghiêng của đường thẳng một cách chính xác.

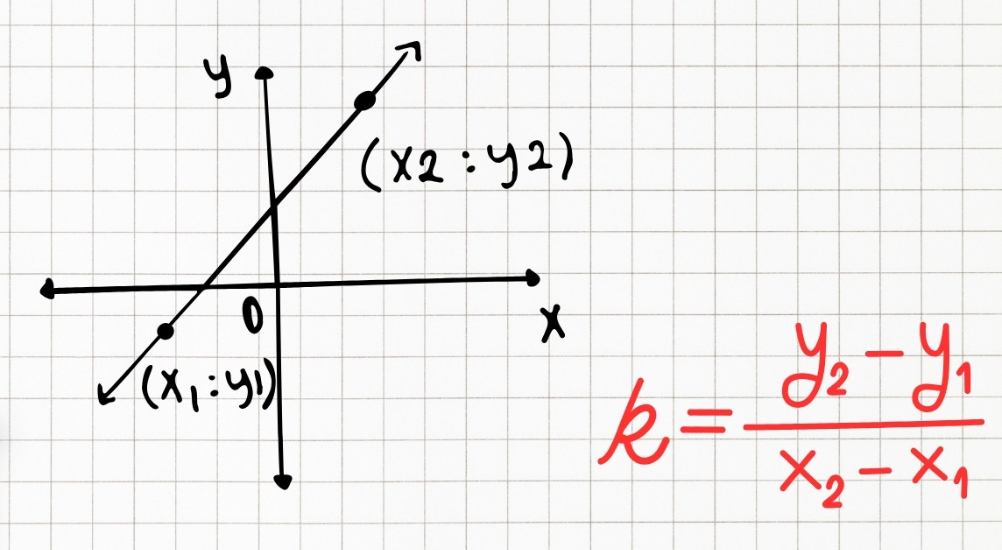
4. Cách tính hệ số góc

Hệ số góc của đường thẳng đo lường góc giữa đường thẳng và trục hoành. Để tính hệ số góc, cần biết hai điểm trên đường thẳng.

Dưới đây là cách tính hệ số góc của đường thẳng:

Bước 1: Xác định hai điểm trên đường thẳng: Gọi tọa độ của hai điểm này lần lượt là (x₁, y₁) và (x₂, y₂).

Bước 2: Tính sự chênh lệch tọa độ theo trục hoành và trục tung: Δy = y₂ - y₁ và Δx = x₂ - x₁.

Bước 3: Tính hệ số góc của đường thẳng bằng cách chia Δy cho Δx: a = Δy/Δx.

Sau khi thực hiện các bước trên, bạn sẽ có hệ số góc của đường thẳng, có thể được biểu diễn dưới dạng số thập phân hoặc phân số. Hệ số góc cho biết độ dốc của đường thẳng; nếu là dương, đường thẳng nghiêng lên, còn nếu âm, đường thẳng nghiêng xuống.

5. Các dạng bài tập về hệ số góc

Dạng 1: Tìm hệ số góc của đường thẳng

Phương pháp giải: Sử dụng kiến thức về vị trí tương đối của hai đường thẳng và hệ số góc của đường thẳng

+ Hai đường thẳng song song

d và d’ song song với nhau khi và chỉ khi

$\left\{\begin{array}{l}a=a\text{'}\\ b\ne b\text{'}\end{array}\right.$

+ Hai đường thẳng vuông góc

$a.a\text{'}=-1$ thì d và d’ là hai đường thẳng vuông góc.

Ví dụ 1: Cho đường thẳng d: y = 2x – 3. Xác định hệ số góc của d.

Lời giải:

Ta có: a = 2 nên hệ số góc của d bằng 2

Ví dụ 2: Cho đường thẳng d: y = ax + b. Xác định hệ số góc của d biết

a) d song song với đường thẳng $d_1$: y = 4x – 1

b) d vuông góc với đường thẳng $d_2$: y = -3x + 1

Lời giải:

a) Vì d // $d_1$$\Rightarrow$a = 4

$\Rightarrow$hệ số góc của d là 4

b) Vì d$\perp d_2$ nên a.( -3) = -1

$\iff$a = (-1) : (-3)

$\iff a=\frac{1}{3}$

Vậy hệ số góc của d là $\frac{1}{3}$.

Ví dụ 3: Tìm hệ số góc của đường thẳng d: y = (m – 5)x – m biết d cắt trục tung tại điểm có tung độ bằng 3.

Lời giải:

Vì d cắt trục tung tại điểm có tung độ bằng 3 nên thay x = 0 và y = 3 vào d ta có:

3 = (m – 5).0 – m

$\iff$m = -3

Với m = -3

$\Rightarrow$a = (-3 – 5) = -8

Vậy hệ số góc của đường thẳng d là -8.

Dạng 2: Xác định góc tạo bởi đường thẳng và tia Ox

Phương pháp giải: Để xác định góc giữa đường thẳng d và tia Ox ta làm như sau:

Cách 1: Vẽ d trên hệ trục tọa độ rồi sử dụng tỉ số lượng giác của tam giác vuông một cách hợp lí

Cách 2: Gọi $\alpha$ là góc tạo bởi tia Ox và d. Ta có:

- Nếu $\alpha <90°$thì $a>0$ và $a=\tan \alpha$

- Nếu $\alpha >90°$ thì $a<0$ và $a=-\tan \left(180°-\alpha \right)$

Ví dụ 1: Tìm góc tạo bởi đường thẳng d: y = -x + 5 với trục Ox.

Lời giải:

Cách 1: Vẽ d lên hệ trục tọa độ

Cho x = 0 $\Rightarrow$y = 5$\Rightarrow$A(0; 5)

Cho y = 0 $\Rightarrow$x = 5$\Rightarrow$B(5; 0)

Vậy d cắt hai trục Oy; Ox tại hai điểm A và B

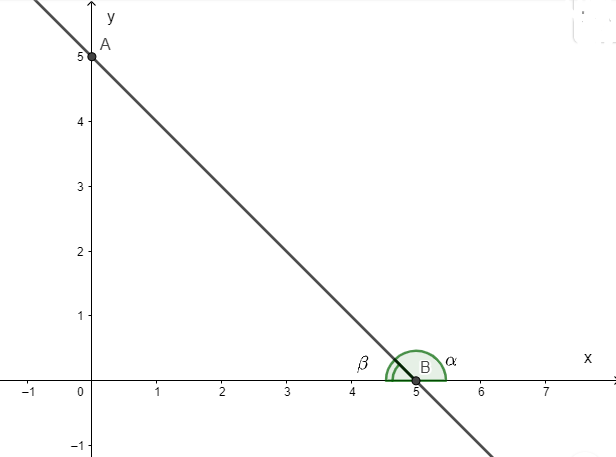
Gọi $\alpha$ là góc tạo bởi d và tia Ox,

Gọi $\beta$ là góc kề bù với góc $\alpha$

Ta có: Tam giác AOB vuông tại O

$\tan \beta =\frac{OA}{OB}=\frac{5}{5}=1$

$\Rightarrow \beta =45°$

Mà $\alpha ,\beta$ là hai góc kề bù

$\Rightarrow \alpha +\beta =180°$

$\iff \alpha =180°-45°$= $135°$

Vậy góc giữa d và Ox là $135°$

Cách 2: vì a = -1 < 0 $\Rightarrow$$\alpha >90°$ và $a=-\tan (180°-\alpha )=-1$

$\Rightarrow \tan (180°-\alpha )=\tan 45°$

$\iff 180°-\alpha =45°$

$\iff \alpha =180°-45°$

$\iff \alpha =135°$

Vậy d tạo với Ox một góc bằng $135°$.

Ví dụ 2: Cho hai đường thẳng d: y = x + 1 và đường thẳng d’: y = $\sqrt{3}x-3$

a) Vẽ d và d’ trên cùng một hệ trục tọa độ

b) Gọi C là giao điểm của d và d’. Gọi A, B lần lượt là giao điểm của d và d’ với trục hoành. Tính các góc của tam giác ABC.

Lời giải:

a)

- Xét d: y = x + 1

Cho y = 0 $\Rightarrow$x = -1$\Rightarrow$A(-1; 0)

Cho x = 0 $\Rightarrow$y = 1$\Rightarrow$A’(0; 1)

$\Rightarrow$d cắt trục hoành và trục tung tại hai điểm A, A’

- Xét d’: y = $\sqrt{3}x-3$

Cho y = 0 $\Rightarrow$x = $\sqrt{3}$$\Rightarrow$B($\sqrt{3}$; 0)

Cho x = 0 $\Rightarrow$y = -3 $\Rightarrow$B’(0; -3)

$\Rightarrow$d’ cắt trục hoành và trục trung tại hai điểm B, B’

Có đồ thị như hình vẽ

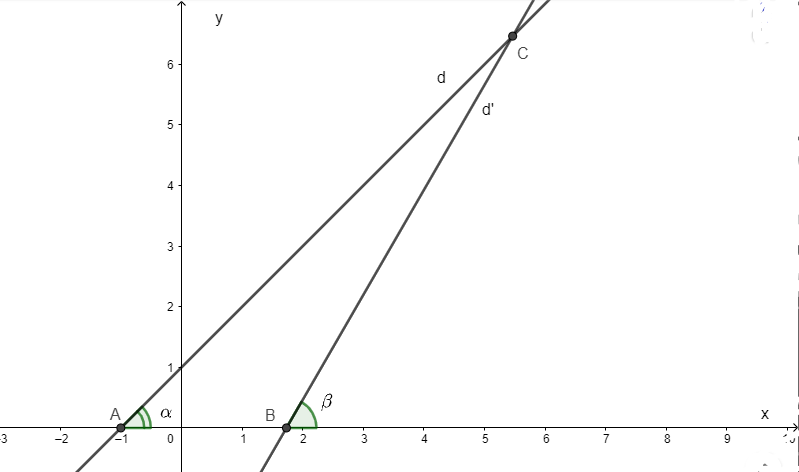
b)

- Gọi $\alpha$ là góc tạo bởi d và Ox

Xét đường thẳng d ta có

a = 1 > 0 $\Rightarrow \alpha <90°$( với $\alpha$ là góc tạo bởi d với Ox)

$\Rightarrow \tan \alpha =a=1$

$\iff \alpha =45°$ $\Rightarrow \widehat{CAB}=45°$

- Gọi $\alpha$ là góc tạo bởi d’ và Ox

Xét đường thẳng d’ ta có:

a’ = $\sqrt{3}$ > 0 $\Rightarrow \beta <90°$(với $\beta$ là góc hợp bởi d’ với Ox)

$\Rightarrow \tan \beta =a\text{'}=\sqrt{3}$

$\iff \beta =60°$

Mà $\widehat{ABC}$ kề bù với $\beta$ nên ta có $\widehat{ABC}$= $180°-60°$= $120°$

$\widehat{ABC}=120°$

Xét tam giác ABC có:

$\widehat{CAB}+\widehat{ABC}+\widehat{BCA}=180°$

$\iff 45°+120°+\widehat{BCA}=180°$

$\iff \widehat{BCA}=180°-45°-120°$

$\iff \widehat{BC}A=15°$.

Dạng 3: Xác định đường thẳng khi biết hệ số góc

Phương pháp giải: Gọi phương trình đường thẳng cần tìm là d: y = ax + b. Ta xác định a, b dựa vào kiến thức góc và hệ số góc.

Gọi đường thẳng cần tìm là y = ax + b (a$\ne$0)

Khi đó hệ số góc của đường thẳng là a

b được xác định sử dụng điều kiện còn lại của đề bài két hợp với a đã tìm được.

Ví dụ 1: Xác định đường thẳng d biết d đi qua A(1; 2) và có hệ số góc là 2.

Lời giải:

Gọi đường thẳng cần tìm là d: y = ax + b (a ≠ 0)

Vì d có hệ số góc là 2 $\Rightarrow$a = 2

Vì d đi qua A(1; 2) nên ta thay x = 1; y = 2 và a = 2 vào d ta được

2 = 2.1 + b

$\iff 2=2+b$

$\iff b=0$.

Vậy đường thẳng cần tìm là y = 2x.

Ví dụ 2: Viết phương trình đường thẳng đi qua B(5; 4) và tạo với trục Ox một góc bằng $45°$.

Lời giải:

Gọi đường thẳng cần tìm là d: y = ax + b (a ≠ 0)

Vì $45°<90°$nên a = $\tan 45°$ = 1

Vì d đi qua B(5; 4) nên ta thay x = 5; y = 4; a = 1 vào d ta được:

4 = 1.5 + b

$\iff 4=5+b$

$\iff b=-1$

Vậy đường thẳng cần tìm là d: y = x – 1.

6. Bài tập về hệ số góc

Bài 1: Cho đường thẳng d: y = ax + 3. Tìm hệ số góc của d biết

a) d song song với đường thẳng y = 2x - 1

b) d vuông góc với đường thẳng y = $\frac{\sqrt{2}}{2}$x – 1.

Bài 2: Cho đường thẳng d: y = ax + $\frac{\sqrt{2}}{2}$. Tìm hệ số góc của d biết

a) d đi qua $A\left(\frac{-\sqrt{2}}{2};1\right)$

b) d song song với đường thẳng y = 3x – 1.

Bài 3: Xác định đường thẳng d biết:

a) d đi qua $A\left(\frac{\sqrt{3}}{2};2\right)$ và có hệ số góc là -2.

b) Đường thẳng d song song với đường thẳng y = 2x + 1 và đi qua B(-2; 3).

Bài 4: Tìm góc tạo bởi trục Ox với đường thẳng d biết

a) d: y = $\frac{1}{\sqrt{3}}$x – 2

b) d đi qua 2 điểm A(0;1) và $B\left(\sqrt{3};0\right)$.

Bài 5: Xác định đường thẳng d biết d đi qua A(2;-3) và tạo với Ox một góc $135°$.

Bài 6: Cho hai đường thẳng d: y = 2x + 4 và d’: y = $\frac{-1}{2}$x – 1.

a) Vẽ hai đường thẳng trên cùng một hệ trục tọa độ

b) Gọi giao điểm của d và d’ với trục tung là B và C. Chứng minh tam giác ABC vuông với A là giao điểm của d và d’

c) Tính các góc tam giác ABC.

Bài 7: Tìm hệ số góc của đường thẳng $△$biết

a) $△$ đi qua $A\left(\sqrt{2};1\right)$ và $B\left(0;1+3\sqrt{2}\right)$

b) $△$ đi qua $C\left(\frac{1}{2};\frac{-1}{4}\right)$ và giao điểm của hai đường thẳng y = 2x – 1 và y = 3x + 2.

Bài 8: Viết phương trình đường thẳng d đi qua $A\left(\frac{1}{3};\frac{-1}{2}\right)$ và có hệ số góc là tung độ của giao điểm hai đường thẳng y = 2x – 5 và y = -x – 1.

Bài 9: Cho đường thẳng d tạo với trục hoành một góc $150°$ và đi qua A(-3;-2).

Tìm tọa độ giao điểm của d với đường thẳng y = 2x + 3.

Bài 10: Cho đường thẳng d: y = $\frac{1}{2}$x + 4 và d’: y = -x + 4. Gọi A, B là giao điểm của d và d’ với trục Ox, C là giao điểm của d và d’.

a) Tìm tọa độ A, B, C.

b) Xác định góc giữa d và d’ tạo với Ox.

c) Tính các góc của tam giác ABC.

d) Tính chu vi tam giác ABC.

e) Tính diện tích tam giác ABC.