15000 câu hỏi ôn tập Toán có đáp án (Phần 97)
Bộ 15000 câu hỏi ôn tập môn Toán có đáp án Phần 97 hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Ngữ văn.
15000 câu hỏi ôn tập Toán (Phần 97)
a) Chứng minh AH vuông góc với BC.
Lời giải:
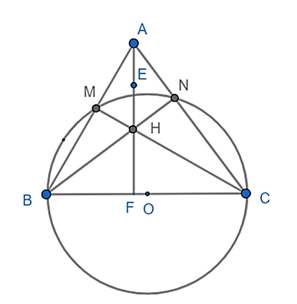
a) Xét (O) có ΔBMC nội tiếp và BC là đường kính
Do đó: ΔBMC vuông tại M
⇒ BM ⊥ MC tại M
⇒ CM ⊥AB tại M
Xét (O) có ΔBNC nội tiếp và BC là đường kính
Do đó: ΔBNC vuông tại N
⇒ BN ⊥ NC tại N
⇒ BN ⊥ AC tại N
Xét ΔABC có BN, CM là đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
⇒ AH ⊥ BC
b) Xét tứ giác AMHN có: ^AMH+^ANH=90°
nên AMHN là tứ giác nội tiếp đường tròn đường kính AH
⇒A, M, H, N cùng thuộc một đường tròn.
Gọi giao điểm của AH với BC là F
Xét ΔABC có: H là trực tâm của ΔABC
F là giao điểm của AH với BC
Do đó: AH ⊥ BC tại F
⇒ ΔAFB vuông tại F
⇒
Mà (do ΔCMB vuông tại M)
Nên:
Lại có:
Vậy EM là tiếp tuyến của (O).
Đề bài: Tính giá trị biểu thức: .
Lời giải:
b) Chứng minh AEB và COD đồng dạng.
Lời giải:
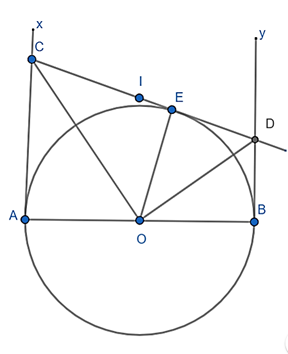
a) Ta có: (2 góc kề bù)
OC là tia phân giác (tính chất 2 tiếp tuyến cắt nhau)
OD là tia phân giác (tính chất 2 tiếp tuyến cắt nhau)
Suy ra:
Xét tam giác ACO và tam giác CEO có:
Chung CO
AC = CE (tính chất hai tiếp tuyến cắt nhau)
Nên: ∆ACO = ∆ECO (c.g.c)
⇒
Chứng minh tương tự, ta có: ∆DOE = ∆DOB (c.g.c)
⇒
Mà:
⇒
Hay , tức
b) Ta có:
(cùng chắn cung OE)
Xét ∆AEB và ∆COD có:
Suy ra: ∆AEB ~ ∆COD (g.g)
c) I là trung điểm của CD, kẻ IO
Ta có: DB ⊥ AB
AC ⊥ AB
⇒ DB // AC
⇒ CDBA là hình thang
⇒ OI là đường trung bình do nối 2 cạnh bên của hình thang
⇒ OI // AC
Mà AC ⊥ AB nên OI ⊥ AB
Vậy AB là tiếp tuyến của (I;IC)
a) Tứ giác ADME là hình gì, tại sao?
d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?
Lời giải:
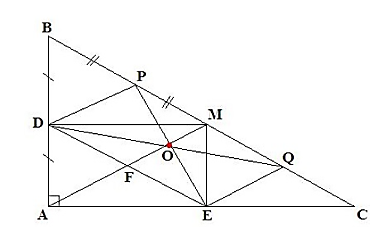
a) Ta có D, E là hình chiếu của M trên AB, AC
Nên DM ⊥ AB và ME ⊥ AC, hay
Xét tứ giác ADME có
Suy ra ADME là hình chữ nhật.
b) Xét ΔABC vuông tại A có M là trung điểm BC
Suy ra AM =
Vì ADME là hình chữ nhật có AM, DE là hai đường chéo, suy ra AM = DE
Mà AM =
Do đó DE = .
c) Ta có AD ⊥ AC và ME ⊥ AC, suy ra AD // ME
Mà M là trung điểm của BC
Suy ra E là trung điểm của AC
Xét tam giác AMC có E, Q lần lượt là trung điểm của AC, MC
Suy ra QE là đường trung bình
Do đó QE // AM, QE = (1)
Ta có DM ⊥ AB và AB ⊥ AC
Suy ra DM // AC
Mà M là trung điểm của BC
Suy ra D là trung điểm của AB
Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM
Suy ra DP là đường trung bình của ΔBAM
Do đó DP // AM và DP = (2)
Từ (1) và (2) suy ra DP // EQ, DP = EQ
Do đó DPQE là hình bình hành.
Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)
Ta có P, Q lần lượt là trung điểm của BM, MC và M là trung điểm BC
Suy ra M là trung điểm PQ
Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ
Suy ra AM là đường trung bình của DPQE
Do đó AM đi qua trung điểm DE, gọi điểm đó là F
Từ đó AM là trục đối xứng của DPQE tức là đi qua O
Vậy tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Để hình bình hành DPQE là hình chữ nhật thì
Ta xét ΔBAM nếu DP ⊥ BM thì AM ⊥ BM
Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao
Suy ra ΔABC vuông cân tại A
Vậy để hình bình hành DPQE là hình chữ nhật thì tam giác vuông ΔABC cần thêm điều kiện cân tại A.
Lời giải:
Ta có:
Suy ra:
Phương trình đường thẳng AB là: 3(x – 1) – 4(y – 2) = 0 ⇔ 3x – 4y + 5 = 0
Tương tự: phương trình đường thẳng BC là: x + 2y + 5 = 0
Phương trình đường thẳng AC: 3x + y – 5 = 0
Để M nằm trong tam giác ABC thì thỏa mãn:
– M, A nằm cùng phía đối với BC
– M, B nằm cùng phía đối với AC
– M, C nằm cùng phía đối với AB
Suy ra M nằm trong miền nghiệm của hệ bất phương trình:
Thay M vào hệ bất phương trình trên ta được:
⇒ –1 < m < 2.
Vậy –1 < m < 2 thì M nằm trong tam giác ABC.
Đề bài: Chứng minh rằng n(n + 13) chia hết cho 2 với mọi số tự nhiên n.
Lời giải:
* Khi n là số chẵn thì n ⋮ 2 với mọi n
Suy ra: n(n + 13) ⋮ 2 với mọi n.
* Khi n là số lẻ, giả sử n có dạng n = 2k + 1 (k là số tự nhiên)
Thì n + 13 = 2k + 1 + 13 = 2k + 14 = 2(k + 7) ⋮ 2 với mọi k.
Suy ra: n(n + 13) = 2(2k + 1)(k + 7) ⋮ 2 với mọi k.
Vậy n(n + 13) chia hết cho 2 với mọi số tự nhiên n.
Đề bài: Chứng minh với mọi tam giác ABC ta có:
cos2A + cos2B + cos2C = –1 – 4cosA.cosB.cosC.
Lời giải:
Xét vế trái:
cos2A + cos2B + cos2C
= (cos2A + cos2B) + 2cos2C – 1
= 2cos(A + B).cos(A − B) + 2cos2C – 1
= −2cosC.cos(A − B) + 2cos2C – 1
= −2cosC[cos(A − B) − cosC] − 1
= −2cosC[cos(A − B) + cos(A + B)] − 1
= −4cosC.cosA.cosB − 1
Vậy cos2A + cos2B + cos2C = –1 – 4cosA.cosB.cosC
Đề bài: Cho biểu thức B = . Tìm các số nguyên a để B nhận giá trị nguyên.
Lời giải:
ĐKXĐ: a > 0, a ≠ 9.
B =
Để B nhận giá trị nguyên thì
Suy ra:
⇒
⇔
⇔
⇔
⇔
⇔
Vậy a = 1 hoặc a = 4.
Đề bài: Điền số thích hợp vào chỗ chấm
Lời giải:
a) 2,5 tấn = 2500kg
5,4 tấn = 5400kg
1,2 kg = 1200g
3,2 yến = 32 kg
0,96 tấn = 960 kg
3,72 tấn = 37,2 tạ
0,12 kg = 120g
2,2hg = 22dag
5,4 tạ = 54 yến
3,39 tấn = 339 yến
0,5 yến = 2kg
2,2 hg = 220g
b) 4987m2 = 49dam2 87m2
320060 dam2 = 32km2 6000m2
125600 m2 = 12hm2 56dam2
9028007 m2 = 9km2 28007m2
c) 5m2 16dam2 = 5,16m2
7m2 5cm2 = 70005m2
68m2 = 68m2
693000m2 = 693ha
0,235km2 = 235ha
25km2 7dm2 = 25,07m2
15km2 68hm2 = 15,68km2
2002cm2 = 0,2002m2
500m2 = 0,05ha
0,058km2 = 5,8ha
9km2 6dam2 = 9,0006km2
75m2 7dam2 = 75,07m2
68063m2 = 0,68063ha
400ha = 4km2
Lời giải:
Có 7 quả cam chia cho 10 người thì mỗi người sẽ được quả cam.
Mà:
Nên mỗi người sẽ được và quả cam.
Vì vậy để không phải cắt bất kì quả cam nào thành phần bằng nhau thì ta phải:
+ Lấy 5 quả, mỗi quả chia thành 2 phần bằng nhau thì ta có được 10 phần.
+ Lấy 2 quả, mỗi quả chia thành 5 phần thì cũng đủ 10 phần cho mọi người.
Đề bài: Không thực hiện tính tổng, chứng minh rằng A = 2 + 22 + 23 + … + 220 chia hết cho 5.
Lời giải:
A = 2 + 22 + 23 + … + 220
A = (2 + 22 + 23 + 24) + (25 + 26 + 27 + 28) + … + (217 + 218 + 219 + 220)
A = 2(1 + 2 + 22 + 23) + 25(1 + 2 + 22 + 23) + … + 217(1 + 2 + 22 + 23)
A = (1 + 2 + 22 + 23)(2 + 25 + … + 217)
A = 15.(2 + 25 + … + 217)
Vì 15 chia hết cho 5 nên 15.(2 + 25 + … + 217) chia hết cho 5.
Vậy A chia hết cho 5.
Lời giải:
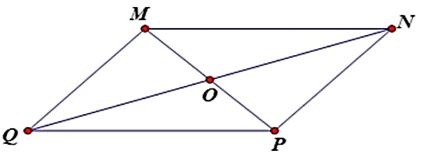
Vì MNPQ là hình bình hành nên cạnh PQ = MN = 6 cm
Lại có: MQ = NP = 5cm
Vì MNPQ là hình bình hành nên O là trung điểm của MP và QN
Suy ra: MP = 2MO = 2.2 = 4(cm)
Vậy PQ = 6cm, MQ = 5cm, MP = 4cm.
Lời giải:
Đổi 150km = 15 000 000 cm
A và B cách nhau 150 km thì trên bản đồ sẽ là số cm là:
15 000 000 : 1 000 000 = 15 (cm)
Đáp số: 15cm.
Lời giải:
Vì đồ thị hàm số y = ax2 + bx + c đi qua điểm A(2; 1) và có đỉnh I(1; –1) nên ta có hệ:
⇔
⇔
⇔
⇔
⇔
Khi đó T = a3 + b2 – 2c = 23 + (–4)2 – 2.1 = 8 + 16 – 2 = 22.
Đề bài: Rút gọn: M = sin(x – y)cosy + cos(x – y)siny.
Lời giải:
M = sin(x – y)cosy + cos(x – y)siny
M = sin[(x – y) + y)]
M = sinx.
Lời giải:
Gọi số học sinh cần tìm là x (x ∈ ℕ*) (học sinh) (350 ≤ x ≤ 400)
Vì số học sinh cần tìm khi xếp hàng 10, hàng 12, hàng 15 đều dư 3 học sinh
⇒ x – 3 chia hết cho 10
⇒ x – 3 chia hết cho 12
⇒ x – 3 chia hết cho 15
⇒ x – 3 ∈ BC(10, 12, 15)
Ta có: 10 = 2.5
12 = 22.3
15 = 3.5
⇒ BCNN(10;12;15) = 22.3.5 = 60
⇒ BC(10;12;15) = B(60) = {0; 60; 120; 180; 240; 300; 360; 420;...}
⇒ x = 3; 63; 123; 183; 243; 303; 363; 423;...
Mà 350 ≤ x ≤ 400
⇒x = 363
Vậy số học sinh khối 6 của trường đó là 363 học sinh.
Đề bài: Cho hình vẽ. Chứng minh rằng:
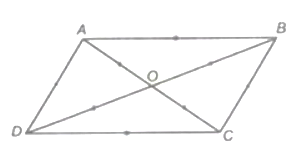
Lời giải:
a) Theo hình vẽ ta có: OA = OB = OC = OD
AC cắt BD tại trung điểm O
Suy ra: ABCD là hình bình hành
Xét ∆AOD và ∆COB có:
AO = BO =
OD = OC
AD = BC (theo hình)
Suy ra: ∆AOD = ∆COB (c.c.c)
b) Theo phần a có: ∆AOD = ∆COB nên
Mà 2 góc này ở vị trí so le trong nên AD // BC.
Lời giải:
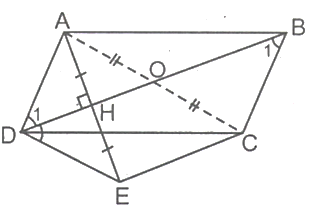
Gọi O là giao điểm của AC và BD, H là giao điểm BD và AE.
Vì E đối xứng với A qua BD nên H là trung điểm của AE.
Xét tam giác ACE có OH là đường trung bình nên OH // CE (O là trung điểm AC, H là trung điểm AE)
Vậy BCED là hình thang.
Xét tam giác ADH và tam giác DHE có:
Chung DH
AH = HE
Nên: ∆ADH = ∆EDH (c.g.c)
Suy ra:
Mà ABCD là hình bình hành nên: (2 góc so le trong)
Lại có:
Vậy BCED là hình thang cân.
Đề bài: Tìm tập giá trị T của hàm số y = sin2x.
Lời giải:
Ta có: –1 ≤ sin2x ≤ 1
Suy ra –1 ≤ y ≤ 1.
Do đó T = [–1; 1].
Lời giải:
Số trang của 1 quyển sách thực tế luôn phải là số chẵn: số trang = số tờ × 2
Vì quyển sách đánh số từ 3 đến 139 nên thực tế quyển sách có 1 trang không được số. Do đó số trang thực tế của quyển sách ban đầu là: 139 – 3 +1 + 1 = 138 trang.
Quay lại bài toán:
Khi đó quyển sách ban đầu có số tờ là: 138 : 2 = 69 tờ
Số tờ bị mất đi do sách cũ là: 2 + 5 = 7 tờ
Vậy sách còn lại số tờ là: 69 – 7 = 62 tờ.
Đề bài: Cho tam giác ABC. Xác định điểm I sao cho vectơ .
Lời giải:
Gọi F là trung điểm của AB.
Ta có:
⇔
⇔
⇔
⇔
⇔
Vậy điểm I là điểm thỏa mãn đẳng thức .
Đề bài: Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB và CD. Tứ giác DEBF là hình gì? Vì sao?
Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB và CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh 3 đường thẳng AC, BD, EF đồng qui.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M, N. Chứng minh tứ giác EMFN là hình bình hành.
Lời giải:
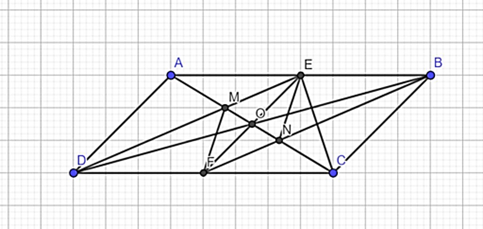
a) Vì ABCD là hình bình hành nên AB // CD, AB = CD
Mà E, F là trung điểm AB, CD nên BE // DF, BE =
Suy ra: DEBF là hình bình hành
b) Gọi O là giao điểm của AC và BD
Vì ABCD là hình bình hành nên O là trung điểm AC và BD
Lại có DEBF là hình bình hành
⇒ DB giao EF tại trung điểm mỗi đường
Vì O là trung điểm BD ⇒ O là trung điểm EF
⇒ AC, DB, EF đồng quy tại O.
c) Vì DEBF là hình bình hành nên DE // BF suy ra: ME // NF
⇒ (O là trung điểm EF)
⇒ OM = ON
⇒ O là trung điểm MN
Vì O là trung điểm MN, EF nên EMFN là hình bình hành.
Đề bài: Cho 2 đường thẳng d1: y = 4x + m – 1, d2: y = x + 15 – 3m.
a) Tìm m để d1, d2 cắt nhau tại điểm C trên trục tung.
b) Với m vừa tìm được, hãy tìm giao điểm A, B của d1, d2 với Ox.
Lời giải:
a) Để (d1) cắt (d2) tại một điểm trên trục tung thì:
⇒ 4m = 16
⇒ m = 4.
b) Với m = 4 ta được (d1): y = 4x + 3
(d2): y = x + 3
Giao điểm của d1 với Ox là A(xA; yA)
Vì A thuộc Ox nên yA = 0
⇒ 4xA + 3 = 0 ⇒ xA =
Vậy giao điểm của d1 với Ox là
Tương tự, ta tìm được giao điểm của d2 với Ox là .
Lời giải:
Gọi 4 số ấy là a, b, c, d
Tổng 2 số bất kì chia hết cho 2 nên a, b, c, d đồng dư với nhau mod 2
Tổng 3 số bất kì chia hết cho 3 nên a, b, c, d đồng dư với nhau mod 3
⇒ a, b, c, d đồng dư với nhau mod 6
Vì a, b, c, d nguyên dương nên giá trị nhỏ nhất mà a, b, c, d có thể nhận là 1
⇒ Các số tiếp theo là 1 + 6 = 7, 7 + 6 = 13, 13 + 6 = 19
⇒ Tổng của a, b, c, d là 1 + 7 + 13 + 19 = 40.
Đề bài: Cho ∆ABC, AQ, BK, CI là 3 đường cao, H là trực tâm.
a. Chứng minh: A, K, B, Q thuộc 1 đường tròn. Xác định tâm của đường tròn.
b. Chứng minh: A, I, H, K thuộc 1 đường tròn. Xác định tâm của đường tròn.
Lời giải:
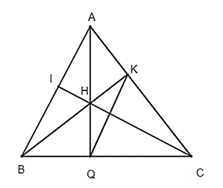
a. Xét tứ giác ABQK có:
Do đó: ABQK là tứ giác nội tiếp hay A, B, Q, K cùng thuộc 1 đường tròn đường kính AB.
Tâm của đường tròn này là trung điểm của AB.
b. Xét tứ giác AIHK có:
Do đó: AIHK là tứ giác nội tiếp hay A, I, H, K cùng thuộc 1 đường tròn đường kính AH.
Tâm của đường tròn này là trung điểm của AH.
b) Chứng minh tam giác CEH cân tại H và HE là tiếp tuyến của (I).
Lời giải:
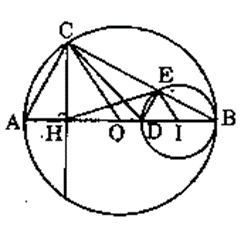
a) ACED là hình thang vuông vì AC // DE (cùng vuông góc với BC)
b) Đặt AB = 2R, AD = 2x, DB = 2y thì HA = HD = x
Ta có các hệ thức sau:
x + y = R hay HI = R
OH = OA – OH = x + y – x = y
Hay OH = y
Xét tam giác OHC và tam giác EIH có:
OH = IE = y
(đồng vị)
OC = IH = R
⇒ ∆OHC = ∆IEH (c.g.c)
Suy ra: HC = EH hay tam giác HCE cân tại H
Lại có: do ∆OHC = ∆IEH nên
Tức HE vuông góc với IE
Vậy HE là tiếp tuyến của (I).
b) Gọi O là giao điểm của AM và KI. Chứng minh .
Lời giải:
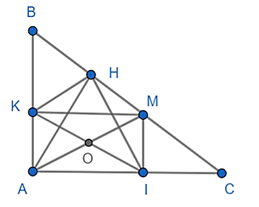
a) Xét tứ giác AIMK có:
Nên AIMK là hình chữ nhật
⇒ AM cắt KI tại trung điểm mỗi đường (tại O) và AM = KI
b) AIMK là hình chữ nhật, O là giao KI và AM
⇒ O là tâm đường tròn ngoại tiếp tứ giác AMKI
Hay A, K, M, I cùng thuộc đường tròn tâm O có bán kính là R = OK = OI = OA = OM
Lại có: mà O là trung điểm AM
Nên OH = OA = OM =
Suy ra: OH = OA = OM = OK = OI
Xét tam giác HIK có: OH = OK = OI =
Suy ra: tam giác HIK vuông tại H hay .
2. Giả sử , hãy tính OM, ON theo R sao cho CM = MN = ND.
Lời giải:
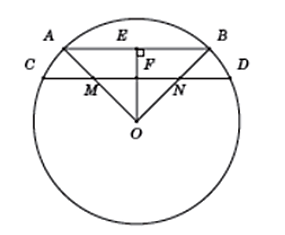
a) Hạ OE vuông góc với AB cắt CD tại F
Trong tam giác OAB cân tại O ta có:
Và MF = NF
Ta nhận xét thêm:
OF ⊥ MN ⇔ OF ⊥ CD ⇔ CF ⊥ DF
Khi đó: CM = CF – MF = DF – NF = DN (đpcm)
b) Đặt MF = x, suy ra:
CF = CM + MF = MN + MF = 3MF = 3x
OF = x, vì tam giác OMF vuông cân tại F
Trong tam giác OCF, ta có:
OF2 = OC2 – CF2
⇔ x2 = R2 – 9x2
⇔ 10x2 = R2
⇔ x =
Khi đó ta được:
ON = OM = OF
Vậy với OM = ON = thỏa mãn điều kiện bài toán.
Lời giải:
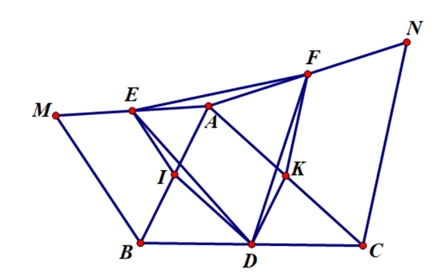
Gọi I là trung điểm AB
Ta có: EI là đường trung bình của tam giác AMB
⇒ EI // MB
⇒
Lại có: EI =
( vì ID // AC)
Xét ∆EID và ∆AEF có:
EI = AE
ID = AF
Suy ra: △EID = △ EAF (c.g.c)
⇒ DE = EF (*) và
Mà
⇒ hay (**)
Từ (*) và (**) suy ra: DEF là tam giác đều.
Đề bài: Cho a, b, c là 3 cạnh của 1 tam giác.
Lời giải:
Vì a, b, c là độ dài 3 cạnh tam giác nên:
A =
⇔
⇔
⇔
⇔
⇔
⇔ A ≥ 3 (đpcm).
Đề bài: Tìm các số nguyên dương x, y, z thỏa mãn x + y + z = xyz.
Lời giải:
Do vai trò bình đẳng của x, y, z trong phương trình, trước hết ta xét x ≤ y ≤ z.
Vì x, y, z nguyên dương nên xyz ≠ 0, do x ≤ y ≤ z
⇒ xyz = x + y + z ≤ 3z
⇒ xy ≤ 3
⇒ xy thuộc {1; 2; 3}.
Nếu xy = 1 ⇒ x = y = 1, thay vào (2) ta có : 2 + z = z, vô lí.
Nếu xy = 2, do x ≤ y nên x = 1 và y = 2, thay vào (2), ⇒ z = 3.
Nếu xy = 3, do x ≤ y nên x = 1 và y = 3, thay vào (2), ⇒ z = 2.
Vậy nghiệm nguyên dương của phương trình (2) là các hoán vị của (1; 2; 3).
Đề bài: Tìm m để phương trình x2 + mx + m – 1 = 0 có hai nghiệm lớn hơn m.
Lời giải:
Ta có: x2 + mx + m – 1 = 0
⇔ (x2 – 1) + m(x + 1) = 0
⇔ (x – 1)(x + 1) + m(x + 1) = 0
⇔ (x + 1)(x – 1 + m) = 0
⇔
⇔
Để phương trình có hai nghiệm lớn hơn m thì: –1 > m và 1 – m > m
Suy ra: m < –1 và m <
Vậy m < –1.
Đề bài: Quan sát hình vẽ sau. Giải thích vì sao m song song với n?
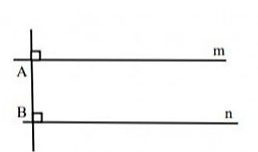
Lời giải:
Dựa vào hình vẽ ta thấy:
suy ra: m // n
(Lý thuyết: Nếu hai đường thẳng (phân biệt) cùng vuông góc với một đường thẳng thứ ba thì song song với nhau).
1) Chứng minh rằng tứ giác DENM là tứ giác nội tiếp.
2) Chứng minh rằng tích AM. AN không đổi.
3) Chứng minh rằng tâm đường tròn ngoại tiếp tứ giác DENM thuộc một đường thẳng cố định.
Lời giải:
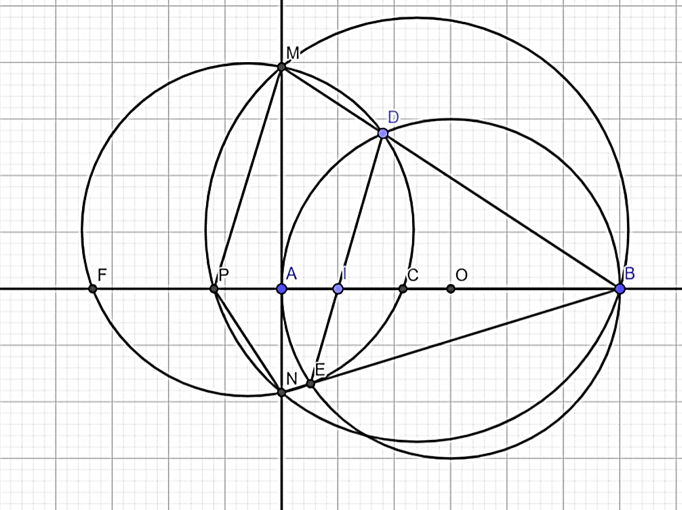
1) Ta có: AB là đường kính của (O) nên AD ⊥ BM, AE ⊥ EB
Mà AB ⊥ MN
Nên BD.BM = BA2 = BE. BN
⇒
Mà
⇒ ∆BDE ∽ ∆BNM (c.g.c.)
⇒
⇒ MNED nội tiếp
2) Vẽ đường tròn ngoại tiếp ΔBMN, (BMN) ∩ AB = P
⇒ ΔBEI ∽ ΔBPN(g.g)
⇒
⇒ BI.BP = BE.BN = BA2
⇒ BP = ⇒ P cố định
Mà
⇒ ΔABM ∽ ΔANP(g.g)
⇒
⇒ AM.AN = AB. AP không đổi
3.Vẽ đường tròn ngoại tiếp DMNE, (DMNE) ∩ AB = C, F (như hình vẽ)
Chứng minh tương tự câu 2 có AF.AC = AM.AN ⇒ AF.AC = AP.AB
Lại có BCF, BDM là cát tuyến tại B với (DMNE)
⇒ BC.BF = BD.BM = BA2
⇒
⇒
⇒
⇒
⇒
⇒
⇒
⇒ ⇒ C cố định
⇒ C, F cố định
⇒ Tâm (DENM) thuộc trung trực của CF cố định.
Đề bài: Cho hình thang ABCD (AD // BC) có .
3) Tính số đo các góc của hình thang.
Lời giải:
1) Vì ABCD là hình thang có AD // BC nên (2 góc trong cùng phía)
2) Lại có: (2 góc trong cùng phía)
Nên:
3) Ta có: ,
⇒
⇒
Lại có: và
⇒ ⇒ ⇒
⇒
Vậy .
Đề bài: Tìm số nguyên tố p sao cho 2p + 1 chia hết cho p.
Lời giải:
Giả sử p là số nguyên tố thỏa mãn 2p + 1 chia hết cho p.
Theo định lý Fermat, ta có: 2p ≡ 2 (mod p)
Suy ra: (2p – 2) ⋮ p
⇒ 3 = (2p + 1) – (2p – 2) ⋮ p
⇒ p = 3 (thỏa mãn)
Vậy số nguyên tố p cần tìm là 3.
a, Chứng minh: BHCK là hình bình hành.
b, Chứng minh: BK vuông góc AB.
c, Chứng minh: tâm giác MEF cân.
d, CQ vuông góc BK tại Q. Chứng minh: EF vuông góc EQ.
Lời giải:
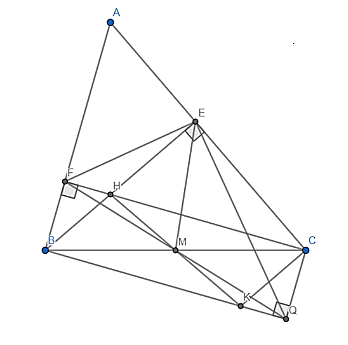
a) Xét tứ giác BHCK có:
M là trung điểm của BC (giả thiết).
M là trung điểm của HK (MH = MK).
⇒ BHCK là hình bình hành (dấu hiệu nhận biết).
b) BHCK là hình bình hành (chứng minh trên).
⇒ BK // HC mà HC ⊥ AB (đường cao)
⇒ AB ⊥ BK (từ vuông góc đến song song đảo).
c) M là trung điểm của BC (giả thiết)
⇒ ME là đường trung tuyến của ΔBCE
Mà ΔBCE vuông tại E ⇒ ME =
M là trung điểm của BC (giả thiết).
⇒ MF là đường trung tuyến của ΔBCF
Mà ΔBCF vuông tại F⇒ MF = = ME
⇒ΔMEF cân (hai cạnh bên bằng nhau).
d) Xét tứ giác BFCQ có:
(CF ⊥ AB)
(BK ⊥ AB)
(CQ ⊥ BK)
⇒ BFCQ là hình chữ nhật
⇒ BC = FQ
⇒ M là trung điểm FQ
⇒ ME là trung tuyến của tam giác EFQ
Suy ra: ME = =
⇒ Tam giác EFQ vuông tại E
Vậy EF vuông góc EQ.
a) Chứng minh rằng: tam giác COB là tam giác vuông.
Lời giải:
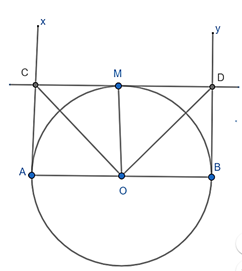
a) Xét (O) có:
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: OC là tia phân giác của góc (1)
Xét (O) có: DM là tiếp tuyến; DB là tiếp tuyến
Do đó OD là tia phân giác của góc (2)
Từ (1) và (2) suy ra:
hay ΔODC vuông tại O.
b) Xét ΔODC vuông tại O có OM là đường cao
Áp dụng hệ thức lượng trong tam giác vuông, có: MC.MD = MO2.
Lời giải:
Δ = (–m + 3)2 – 4.(–5) = m2 – 6m + 9 + 20 = m2 – 6m + 29 = (m – 3)2 + 20 > 0
Nên phương trình luôn có hai nghiệm phân biệt.
Để phương trình có hai nghiệm phân biệt x1, x2 là các số nguyên thì trước hết Δ phải là một số chính phương.
Giả sử (m – 3)2 + 20 = k2 với k nguyên
⇒ k2 – (m – 3)2 = 20
⇔ (k – m – 3)(k – m + 3) = 20
Do (k – m – 3) + (k – m + 3) = 2k chẵn nên chúng cùng tính chẵn lẻ.
Mà 20 là số chẵn nên (k – m – 3) + (k – m + 3) cùng là số chẵn
Suy ra: ⇔ .
Đề bài: Tìm các số tự nhiên x sao cho 14 chia hết cho 2x + 1.
Lời giải:
Ta có: 14 ⋮ (2x + 1) nên (2x + 1) là ước của 14
Ư(14) = {1; 2; 7; 14}
Suy ra: 2x + 1 ∈ {1; 2; 7; 14}
⇒ x ∈ {0; 0,5; 3; 6,5}
Mà x là số tự nhiên nên x = 0 hoặc x = 3.
Vậy x = 0 hoặc x = 3.
Đề bài: Cho A = 2 + 22 + 23 + … + 260. Hãy thu gọn tổng A.
Lời giải:
A = 2 + 22 + 23 + … + 260
2A = 22 + 23 + …. + 261
2A – A = (22 + 23 + …. + 261) – (2 + 22 + 23 + … + 260)
A = 261 – 2.
Đề bài. Cho hai tập hợp khác rỗng A = [ m – 1; 5) và B =[–3; 2m + 1]. Tìm m để A ⊂ B.
Lời giải:
Điều kiện tồn tại nửa đoạn và đoạn:
⇒ –2 ≤ m < 6.
A ⊂ B thì ⇒ m > 2
Kết hợp điều kiện ta được: 2 < m < 6.
Đề bài. Cho tổng A = 8 + 12 + x với x thuộc ℕ. Tìm x để:
Lời giải:
Ta có: A = 8 + 12 + x = 20 + x
a) Để A chia hết cho 2 thì 20 + x chia hết cho 2
Mà 20 luôn chia hết cho 2 nên x chia hết cho 2
Suy ra: x = 2k (k ∈ ℕ).
b) Để A không chia hết cho 2, thì (20 + x) không chia hết 2
Mà 20 luôn chia hết cho 2 nên để 20 + x 2 thì x 2
Suy ra: x = 2k + 1 (k ∈ ℕ).
Đề bài. Điền chữ số thích hợp vào dấu * để được số M = thỏa mãn điều kiện:
a) M chia hết cho 3;
b) M chia hết cho 9;
c) M chia hết cho 3 nhưng không chia hết 9.
Lời giải:
a) Để M chia hết cho 3 thì tổng các chữ số của M chia hết cho 3
⇒ (3 + 7 + *) ⋮ 3 hay (10 + *) ⋮ 3
Vì * < 10 nên * ∈ {2; 5; 8}
b) Để M chia hết cho 9 thì tổng các chữ số của M chia hết cho 9
⇒ (3 + 7 + *) ⋮ 9 hay (10 + *) ⋮ 9
Vì * < 10 nên * ∈ {8}
c) Để M chia hết cho 3 thì tổng các chữ số của M chia hết cho 3
⇒ (3 + 7 + *) ⋮ 3 hay (10 + *) ⋮ 3
Vì * < 10 nên * ∈ {2; 5; 8}
Ta loại * = 8 vì khi * = 8 ta được số 378 là số chia hết cho 9.
Vậy * ∈ {2; 5}.
Đề bài. Thực hiện phép tính .
Lời giải:
Ta xét tổng quát:
Khi đó ta có:
Đề bài. Cho phương trình: x2 – 2mx + m2 – 4 = 0.
a) Chứng minh rằng phương trình luôn có 2 nghiệm với mọi giá trị của m.
b) Tìm m để phương trình có 2 nghiệm phân biệt x1; x2 sao cho 3x1 + 2x2 = 7.
Lời giải:
a) x2 – 2mx + m2 – 4 = 0
∆' = m2 – m2 + 4 = 4 > 0 nên phương trình luôn có 2 nghiệm với mọi giá trị của m.
b) Phương trình có 2 nghiệm phân biệt là:
TH1: x1 = m + 2; x2 = m – 2
Khi đó: 3x1 + 2x2 = 7
⇔ 3(m + 2) + 2(m – 2) = 7
⇔ 5m + 6 – 4 – 7 = 0
⇔ 5m – 5 = 0
⇔ m = 1.
TH2: x2 = m + 2; x1 = m – 2
Khi đó: 3x1 + 2x2 = 7
⇔ 3(m – 2) + 2(m + 2) = 7
⇔ 3m – 6 + 2m + 4 – 7 = 0
⇔ 5m – 9 = 0
⇔ m =
Vậy m = 1 hoặc m = .
Đề bài. Biến đổi tổng thành tích A = sina + sinb + sin(a + b).
Lời giải:
A = sina + sinb + sin(a + b)
Đề bài. Cho số tự nhiên bằng ba lần tích các chữ số của nó.
a) Chứng minh rằng b chia hết cho a.
b) Gỉa sử b = ka (k thuộc ℕ) chứng minh rằng k là ước của 10.
Lời giải:
a) Theo đề bài có:
⇔ 10a + b = 3ab (1)
Vì 3ab ⋮ a nên (10a + b) ⋮ a
Mà 10a ⋮ a nên b ⋮ a.
b) Do b = ka mà b < 10 nên ka < 10
Thay b = ka vào (1) ta được:
10a + ka = 3a.ka
⇔ a(10 + k) = 3a2.k
⇔ 10 + k = 3ak (*)
Vì 3ak ⋮ k nên 10 + k ⋮ k
Mà k ⋮ k nên 10 ⋮ k
Vậy k là ước của 10.
c) Theo phần b có k là ước của 10 nên k ∈ {1; 2; 5}
Với k = 1 thay vào (*) có: 11 = 3a (loại vì a là số tự nhiên)
Với k = 2 thay vào (*) có: 12 = 6a ⇒ a = 2
b = ka = 2a = 2.2 = 4
Với k = 5 thay vào (*) có: 15 = 15a ⇒ a = 1
b = ka = 5a = 5
Vậy số cần tìm là 24 và 15.
Đề bài. Cho tam giác ABC nhọn (AB < AC) có các đường cao BD và CE.
a, Cho góc A = 60 độ và AC = 12cm, tính AE và CE.
b, Tia DE cắt BC ở F. Chứng minh tam giác ADE đồng dạng với tam giác ABC.
Lời giải:
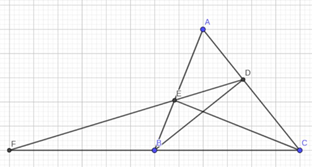
a) Ta có:
AE =
b) Xét ΔADB, ΔAEC có:
Chung
⇒ ΔADB ∽ ΔAEC(g.g)
⇒
Mà
⇒ ΔADE ∽ ΔABC (c.g.c)
c) Từ câu b: ΔADE ∽ ΔABC suy ra:
⇒
Mà
Xét ΔFBE và ΔFDC có:
⇒ ΔFBE ∽ ΔFDC(g.g)
⇒
⇒ FB.FC = FD.FE.
Đề bài. Cho nửa đường tròn (O; R). Hai dây cung AB và CD song song với nhau có độ dài lần lượt là 32 cm và 24 cm và khoảng cách giữa 2 dây là 4 cm. Tính bán kính đường tròn.
Lời giải:
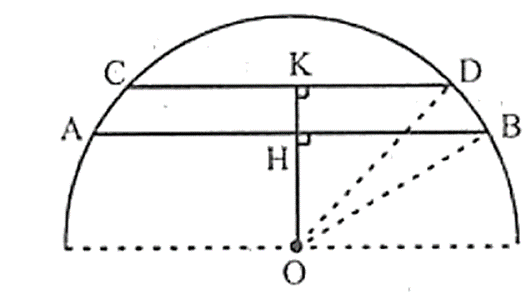
Kẻ OH vuông góc với AB, OK vuông góc với CD
Ta thấy O, H, K thẳng hàng
Đặt OH = x, OK = x + 4
Tam giác OHB vuông tại H có:
OH2 + HB2 = OB2 hay x2 + 162 = R2
Tam giác OKD vuông ở K có:
OK2 + KD2 = OD2
Hay (x + 4)2 + 122 = R2
Từ (1) và (2) suy ra: x2 + 162 = (x + 4)2 + 122
Giải phương trình này ta được: x = 12, tức OH = 12 cm
Từ (1) ta có: R2 = 122 + 162 = 400, suy ra R = 20 cm.
c) Gọi I là giao điểm của DE và BC. Chứng minh HI là tiếp tuyến của đường tròn đường kính EB?
Lời giải:
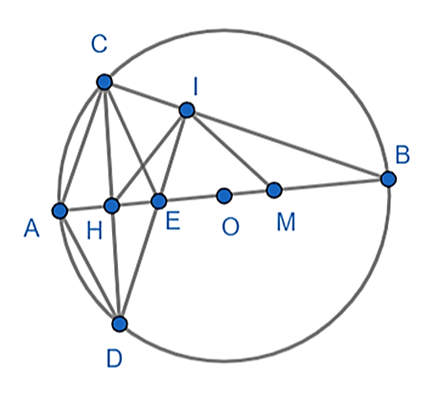
a) Vì là góc nội tiếp chắn nửa đường tròn nên
b) Xét (O) có:
OH là một phần đường kính
CD là dây
OH ⊥ CD tại H
Do đó: H là trung điểm của CD
Xét tứ giác ECAD có
H là trung điểm của đường chéo CD
H là trung điểm của đường chéo EA
Do đó: ECAD là hình bình hành
Mà EA ⊥ CD
Nên ECAD là hình thoi
c) ACED là hình thoi nên DE //AC
Mà AC ⊥ BC nên DE ⊥ BC
Suy ra: DI ⊥ BC
⇒
Xét tam giác CID vuông tại I có IH là trung tuyến
⇒ IH
⇒ ∆DHI cân tại H ⇒
Gọi M là trung điểm BE
Suy ra: IM là trung tuyến của ∆IBE vuông tại I.
⇒ IM =
⇒ ∆MBI cân tại M
⇒
Ta có:
Suy ra: HI ⊥ IM tại I.
Vì IM = EM = BM = và HI ⊥ IM nên HI là tiếp tuyến của .
Lời giải:
Chu vi phần có dạng hình thang cân:
40 + 50 + 2.15 = 120(cm)
Số mét dây thép cần dùng là:
120 + 10 = 130 (cm) = 1,3 (m)
Vậy cần dùng 1,3m dây thép.
Đề bài. Chứng minh rằng 109 + 108 + 107 chia hết cho 222.
Lời giải:
Ta có: 109 + 108 + 107 = 107(102 + 10 + 1) = 107 . 111
= 106.10.111
= 106.5.2.111
= 106.5.222
Ta thấy 222 chia hết cho 222 nên 106.5.222 chia hết cho 222
Vậy 109 + 108 + 107 chia hết cho 222.
Lời giải:
Số xe trường cần là:
1055 : 30 = 35 ( chiếc ) dư 5 học sinh
Vì thế nên cần thêm 1 xe để chở 5 học sinh còn lại.
Vậy cần ít nhất 36 xe để chở hết học sinh của trường đi dã ngoại.
Đề bài. Cho tam giác ABC vuông tại A. M là trung điểm BC, D đối xứng với A qua M.
a) Chứng minh ABCD là hình chữ nhật.
b) Lấy E đối xứng với A qua C. O là trung điểm CD. Chứng minh B đối xứng với E qua O.
Lời giải:
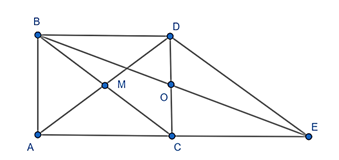
a) Vì ABC là tam giác vuông tại A có AM là đường trung tuyến nên AM =
Lại có: D là đối xứng của A qua M nên MA = MD
Suy ra: MA = MD = MB = MC hay BC và AD cắt nhau tại trung điểm M mỗi đường
⇒ ABCD là hình bình hành
Mà
⇒ ABCD là hình chữ nhật
b) Vì ABCD là hình chữ nhật nên BD // AC và BD = AC
Suy ra: BD // CE (1)
E là đối xứng của A qua C nên AC = CE
Mà AC = BD nên BD = CE (2)
Từ (1) và (2): BDEC là hình bình hành
⇒ DC và BE cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm DC nên O là trung điểm BE
Vậy E đối xứng với B qua O.
b) Gọi M là trung điểm của BC. Chứng minh: ΔBHM = ΔAKM.
Lời giải:
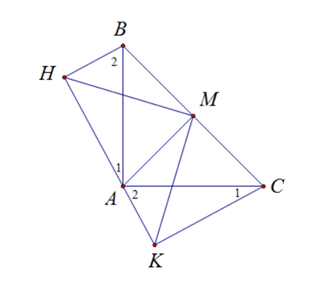
a)
Suy ra:
Xét tam giác vuông HBA và KAC có:
AB = AC (tam giác ABC vuông cân tại A)
⇒ ∆HBA = ∆KAC (g.c.g)
⇒ BH = AK
b) Vì tam giác ABC vuông cân tại A nên AM là đường phân giác, đường cao
⇒ ;
Vậy
Mà theo phần a có:
⇒
Hay
Xét tam giác BHM và AKM có:
BM = AM =
BH = AK
⇒ ∆BHM = ∆AKM (c.g.c)
c) Theo phần b có: ∆BHM = ∆AKM nên MH = MK (2 cạnh tương ứng) (*)
Xét tam giác MKC và tam giác MHA có:
MH = MK
AH = KC (vì ∆HBA = ∆KAC theo phần a)
MC = MA =
⇒ ∆MKC = ∆MHA (c.c.c)
⇒
Mà (vì AM là đường cao của ABC)
Nên: hay (**)
Từ (*) và (**) suy ra: tam giác MHK vuông cân tại M.
Đề bài. Cho tam giác ABC vuông tại A, AH là đường cao. Biết ; AB = 15cm.
b) Gọi E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh: AH3 = BC.BE.CF.
Lời giải:
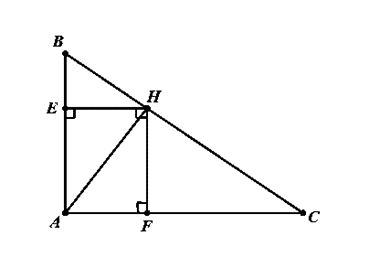
a) Ta có: , nên AH = AC
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AB.AC = BC.AH
⇔ BC =
Suy ra: BC = 15. (cm)
Lại có: AB2 = BC.BH ⇒ BH =
CH = BC – BH = 25 – 9 = 16 (cm).
b) Áp dụng hệ thức lượng trong các tam giác vuông ABC, AHB, AHC ta có:
AB.AC = BC.AH ⇒
BH2 = AB.BE ⇒
CH2 = AC.CF ⇒
Khi đó: (Vì AH2 = BH.CH)
Vậy BC.BE.CF = .
Đề bài. Rút gọn biểu thức P = .
Lời giải:
P =
P =
P =
P =
P =
P =
P = 6 – 112
P = 6 – 121
P = –115.
Lời giải:
Diện tích hình vuông được ghép là:
722.1.2 = 1444 (cm2)
Mà 1444 = 38.38 nên cạnh của hình vuông được ghép là 38cm.
Chu vi hình vuông được ghép là:
38.4 = 152 (cm)
Chu vi của 722 hình chữ nhật là:
722.(1 + 2).2 = 4332 (cm)
Chu vi của hình đã bị giảm:
4332 – 152 = 4180 (cm).
Lời giải:
Gọi số thứ nhất và số thứ hai là x (vì số thứ nhất = số thứ hai)
Ta có: x – 28 + x + 35 = 357
⇔ 2x = 357 – 35 + 28
⇔ 2x = 350
⇔ x = 350 : 2
⇔ x = 175
Vậy số thứ nhất và số thứ hai là 175.
Lời giải:
Số bé nhất có hai chữ số chia hết cho 3 là 12.
Số lớn nhất có 2 chữ số chia hêt cho 2 là 98.
Nên số lớn là:
(98 + 12) : 2 = 55.
Số bé là:
98 – 55 = 43.
Đáp số: số lớn: 55; số bé: 43.
Lời giải:
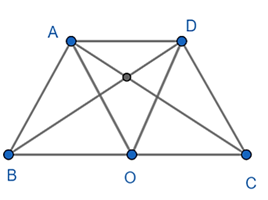
Xét tam giác ABC thấy BC2 = AC2 + AB2 (202 = 162 + 122)
Nên tam giác ABC vuông tại A
Gọi O là trung điểm BC
Nên OB = OC
Vì tam giác ABC vuông tại A nên OA = (1)
Lại có: ABCD là hình thang cân nên AC = BD; AB = DC (tính chất)
⇒ BD = 16cm, DC = 12cm
Lại có: BD2 + DC2 = BC2 (do 202 = 162 + 122)
Nên ∆BDC vuông tại D.
Suy ra: (2)
Từ (1) và (2): OA = OB = OC = OD
Vậy A, B, C, D cùng thuộc đường tròn tâm O, bán kính R = OA.
R = OA=
Vậy bán kính của đường tròn ngoại tiếp ABCD bằng 10 cm.
Đề bài. Giải phương trình: .
Lời giải:
ĐKXĐ:
Phương trình ⇔
Bình phương 2 vế ta được:
x2 – 5x + 4 = – 2x2 – 3x + 12
⇔ 3x2 + 2x – 8 = 0
⇔ 3x2 + 6x – 4x – 8 = 0
⇔ 3x(x + 2) – 4(x + 2) = 0
⇔ (x + 2)(3x – 4) = 0
⇔
Vậy x = –2.
Lời giải:
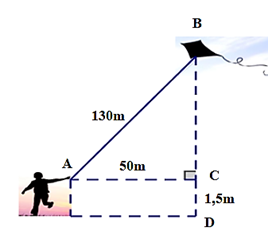
Gọi tay của bạn học sinh là điểm A, diều là điểm B, BC, BD là đường thẳng đứng.
Như vậy đoạn dây từ tay bạn đến diều dài 130m nên ta có AB = 130m, bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 50m nên AC = 50m.
Tay bạn cách mặt đất 1,5m nên CD = 1,5m.
Áp dụng định lý Pitago vào Δ vuông ABC ta có:
BC² = AB² – AC² = 130² – 50² = 14400 ⇒ BC = 120m
⇒ Độ cao của con diều so với mặt đất là đoạn BD là:
BD = BC + CD = 120 + 1,5 = 121,5m.
Đề bài. Tìm x biết: (x + 7) – 25 = 13.
Lời giải:
(x + 7) – 25 = 13
⇔ x + 7 = 13 + 25
⇔ x + 7 = 38
⇔ x = 38 – 7
⇔ x = 31
Vậy x = 31.
Đề bài. Cho tứ giác ABCD có AB = AD, CB = CD, .
a) Chứng minh AC là đường trung trực của BD.
Lời giải:
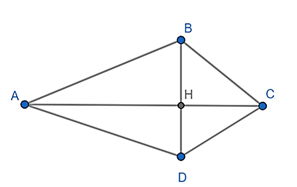
a) Theo giả thiết có AB = AD suy ra tam giác ABD cân tại A
Nên đường thẳng kẻ từ A xuống BD vừa là đường cao vừa là phân giác vừa là đường trung trực, tức A thuộc đường trung trực của BD. (1)
Lại có: CD = CB ⇒ Tam giác CBD cân tại C
⇒ Đường thẳng kẻ từ C xuống đáy BD vừa là đường cao vừa là phân giác vừa là đường trung trực, tức C thuộc đường trung trực của BD (2)
Từ (1) và (2): AC là đường trung trực của BD.
b) Xét ∆ABC và ∆ADC có:
AB = AD
BC = DC
AC chung
⇒ ∆ABC = ∆ADC (c.c.c)
⇒
Mà CH là phân giác của nên
AH là phân giác nên
Lại có trong tam giác ABC có:
⇒
Vậy .
Lời giải:
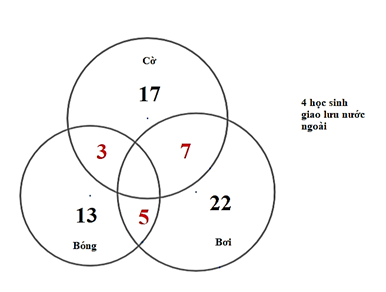
Số học sinh chỉ chơi đá bóng là:
13 – 3 – 5 = 5 (học sinh)
Số học sinh chỉ bơi lội là:
22 – 5 – 7 = 10 (học sinh)
Số học sinh chỉ chơi cờ là:
17 – 3 – 7 = 7 (học sinh)
Tổng số học sinh của lớp đó là:
5 + 10 + 7 + 5 + 3 + 7 + 4 = 41 (học sinh).
Lời giải:
Chu vi của bánh xe đạp là:
2π . 50 = 100π (cm)
Quãng đường đi được là:
100π . 5 = 500π (cm)
Đáp số: 500π (cm).
Đề bài. Giải phương trình: tan2x + cot2x = 1 + .
Lời giải:
ĐKXĐ: cosx ≠ 0; sinx ≠ 0
Xét VT = tan2x + cot2x = (tanx – cotx)2 + 2 ≥ 2
Lại có
⇒
Đẳng thức xảy ra khi và chỉ khi:
⇔
⇔ ⇔ ⇔ .
Đề bài. Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5; 6; 13.
Lời giải:
C = 5 + 52 + … + 520
C = 5(1 + 5 + 52 + … + 519) ⋮ 5
Vậy C chia hết cho 5.
* C = 5 + 52 + … + 520
C = (5 + 52) + (53 + 54) + … + (519 + 520)
C = 5(1 + 5) + 53(1 + 5) + …. + 519(1 + 5)
C = 5.6 + 53.6 +… + 519.6
C = 6(5 + 53 + …. + 519)
Vì 6 ⋮ 6 nên 6(5 + 53 + …. + 519) ⋮ 6
Vậy C chia hết cho 6.
* C = 5 + 52 + … + 520
C = (5 + 52 + 53 + 54) + … + (517 + 518 + 519 + 520)
C = 5.(1 + 5 + 52 + 53) + … + 517(1 + 5 + 52 + 53)
C = 5.156 + 55.156 + … + 517.156
C = 156.(5 + 55 + … + 517)
Vì 156 ⋮ 13 nên 156.(5 + 55 + … + 517) ⋮ 13
Vậy C chia hết cho 13.
Lời giải:
Cạnh hình vuông:
20 : 4 = 5 (cm)
Chiều dài hình chữ nhật là:
26 : 2 – 5 = 8 (cm)
Diện tích hình chữ nhật là:
8 . 5 = 40 (cm2)
Đáp số: 40cm2.
Lời giải:
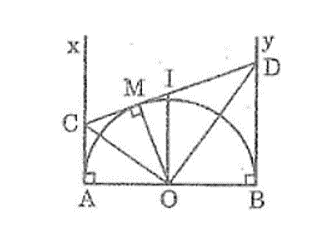
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang.
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC.
Suy ra: OI // AC ⇒ OI ⊥ AB.
Vì OC và OD lần lượt là phân giác của và nên OC vuông góc với OD (tính chất hai góc kề bù).
Suy ra: = 90°
Suy ra: IC = ID = IO = .CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD.
Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Lời giải:
Phân số chỉ 11 quyển sách là:
(số sách ngăn trên)
Ngăn trên có số sách là:
11 : = 42 (quyển)
Trên giá có số sách là:
42 : 6 . (5 + 6) = 77 (quyển)
Đáp số: 77 quyển sách.
Đề bài: Cho A = 2 + 22 + 23 + … + 260. Chứng minh rằng A chia hết cho 3; 5; 7.
Lời giải:
A = (2 + 22) + (23 + 24) +…. + (259 + 260)
A = 2(1 + 2) + 23(1 + 2) + … + 259(1 + 2)
A = 2.3 + 23.3 + … + 259.3
A = 3.(2 + 23 + … + 259)
Vì 3 chia hết cho 3 nên 3.(2 + 23 + … + 259) chia hết cho 3.
Vậy A chia hết cho 3.
* Xét: A = (2 + 22 + 23 + 24) + (25 + 26 + 27 + 28) +…. + (257 + 258 + 259 + 260)
A = 2(1 + 2 + 22 + 23) + 25(1 + 2 + 22 + 23) + … + 257(1 + 2 + 22 + 23)
A = 2.15 + 25.15 + …. + 257.15
A = 15.(2 + 25 + … + 257)
Vì 15 chia hết cho 5 nên 15.(2 + 25 + … + 257) chia hết cho 5.
Vậy A chia hết cho 5.
* Lại có: A = (2 + 22 + 23) + (24 + 25 + 26) +…. + (258 + 259 + 260)
A = 2(1 + 2 + 22) + 24(1 + 2 + 22) + … + 258(1 + 2 + 22)
A = 2.7 + 24.7 + … + 258.7
A = 7(2 + 24 + ... + 258)
Vì 7 chia hết cho 3 nên 7.(2 + 24 + … + 258) chia hết cho 7.
Vậy A chia hết cho 7.
Đề bài: Tìm các số nguyên n biết 3n – 1 chia hết cho n – 2.
Lời giải:
Ta có: 3n – 1 = 3(n – 2) + 5
Để 3n – 1 chia hết cho n – 2 thì 3(n – 2) + 5 chia hết cho n – 2
Mà 3(n – 2) ⋮ (n – 2) nên 5 chia hết cho (n – 2)
⇒ n – 2 ∈ Ư(5)
⇒ n – 2 ∈ {–5; –1; 1; 5}
⇒ n ∈ {–3; 1; 3; 7}
Vậy n ∈ {–3; 1; 3; 7}.
Lời giải:
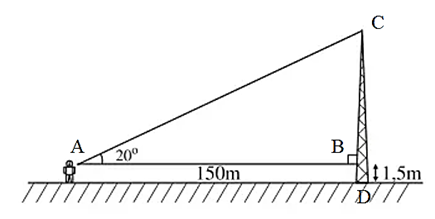
Xét tam giác ABC vuông tại B
Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ta có:
BC = AB.tan = 150.tan20° ≈ 54,596 (m)
Chiều cao của tháp là:
CD = DB + BC = 1,5 + 54,596 = 56,096 (m).
Lời giải:
Cách 1: Coi giá mua là 100% thì giá bán để lãi 20% so với giá mua tức là em bán 120% giá mua. Còn lãi 20% giá bán thì em lấy vốn mua vào
100 : (100 – 20) . 100 = 125% (giá mua)
40 000 đồng chính là:
125% – 100% = 5% (giá mua)
Anh tính ra giá mua giúp cô ấy được:
40 000 : 5 . 100 = 800 000 (đồng).
Và tính luôn giá chém khách tới bến:
800 000 : 4 . 5 = 1 000 000 (đồng).
Cách 2: Khi bán lãi 20% giá bán tức là giá mua so với giá bán chiếm số % là:
100% – 20% = 80% (giá bán)
Khi đó lãi so với giá mua chiếm số phần trăm
20% : 80% = 0,25 = 25% (giá mua)
So với lúc trước lãi tăng thêm số % so với giá mua
25% – 20% = 5%
Giá tiền mua tấm vải
40 000 : 5 . 100 = 800 000 (đồng)
Giá bán tấm vải ( trước khi tăng giá )
800 000 : 100 . (100 + 20) = 960 000 (đồng)
Giá bán tấm vải sau khi tăng giá
800 000 : 100 . (100 + 25) = 1 000 000 (đồng).
Đề bài: Cho C = 1 + 4 + 42 + 43 +… + 42021. Chứng minh C chia hết cho 21.
Lời giải:
C = 1 + 4 + 42 + 43 +… + 42021
C = (1 + 4 + 42) + (43 + 44 + 45) + … + (42019 + 42020 + 42021)
C = (1 + 4 + 42) + 43(1 + 4 + 42) + … + 42019(1 + 4 + 42)
C = 21 + 43.21 +… + 42019.21
C = 21(1 + 43 +… + 42019)
Vì 21 chia hết cho 21 nên 21(1 + 43 +… + 42019) chia hết cho 21
Vậy C chia hết cho 21.
b) Chứng minh AI vuông góc EF.
c) Gọi M là trung điểm HB, N là trung điểm HC. Chứng minh EMNF là hình thang vuông.
Lời giải:
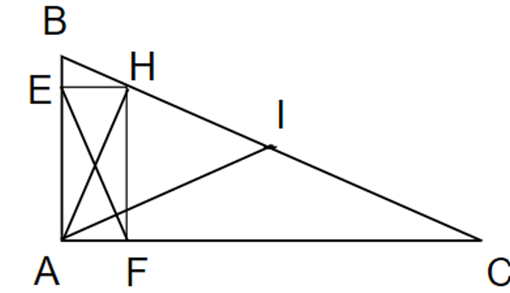
a) Ta có nên EAFH là hình chữ nhật
Suy ra EF = AH (hai đường chéo của một hình chữ nhật)
b) Tam giác ABC vuông tại A có trung tuyến AI
Suy ra AI = = BI = IC
⇒ΔIAB cân tại I nên (1)
EAFH là hình chữ nhật suy ra EF = AH
Gọi O là giao điểm EF và AH
Suy ra EO = OF = OA = OH hay tam giác EOA cân tại O
Nên (2)
Mà
Từ (1), (2) và (3) suy ra hay AI ⊥ EF
c) Xét tam giác EBH vuông tại E có EM là trung tuyến ứng với cạnh huyền
⇒ EM = MB =
⇒ ΔEMB cân tại M
⇒
Mà (do tam giác ABC vuông tại A)
(= )
⇒
⇒
Suy ra: ME vuông góc với EF tại E
Chứng minh tương tự: NF vuông góc với EF tại F
Xét tứ giác MEFN có ME ⊥ EF; NF ⊥ EF
Suy ra: ME // NF
⇒ MENF là hình thang
Đồng thời
⇒ MEFN là hình thang vuông tại E và F.
Lời giải:
Nếu 3a + b ⋮ 7 thì (3a + b)2 ⋮ 49
Tức là A = 9a2 + 6ab + b2 ⋮ 49
Đặt B = 5a2 + 15ab – b2
Ta có: A + B = 14a2 + 21ab = 7(2a + 3b) = 7(9a – 7a + 3b) = 7.3.(3a + b) – 49a ⋮ 49
Từ đó ta được A + B ⋮ 49
Mà A ⋮ 49 nên B ⋮ 49
Ngược lại, nếu B ⋮ 49 ⇒ B = 5a2 + 15ab – b2 ⋮ 7
⇒ (14a2 + 21ab) – (5a2 +15ab – b2) ⋮ 7
⇒ (3a + b)2 ⋮ 7
⇒ (3a + b) ⋮ 7.
Lời giải:
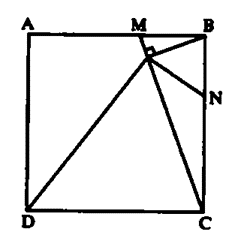
Đặt a là độ dài các cạnh của hình vuông, α =
Ta có: (vì )
=
= –HB.a.cosφ + BN.HC.cosφ
= –MB.a.cos2φ + NB.a.cos2φ
= 0 (vì MB = NB)
Suy ra:
Vậy = 90°.
Đề bài: Cho B = 1 + 3 + 32 + 33 + … + 3101. Chứng minh rằng B chia hết cho 13.
Lời giải:
B = 1 + 3 + 32 + 33 + … + 3101
B = (1 + 3 + 32) + (33 + 34 + 35) + … + (399 + 3100 + 3101)
B = (1 + 3 + 32) + 33(1 + 3 + 32) + … + 399(1 + 3 + 32)
B = (1 + 3 + 32)(1 + 33 +… + 399)
B = 13.(1 + 33 +… + 399)
Vì 13 chia hết cho 13 nên 13.(1 + 33 +… + 399) chia hết cho 13
Vậy B chia hết cho 13.
Đề bài: Cho A = (2m – 1; m + 3) và B = (–4; 5). Tìm m sao cho A ⊂ B.
Lời giải:
Để A ⊂ B thì phải đồng thời xảy ra 2 bất đẳng thức:
2m – 1 ≥ – 1 (hay m ≥ 0) và 2m + 3 ≤ 1 (hay m ≤ – 1)
Nhưng 2 bất đẳng thức trên không thể xảy ra đồng thời nên không có giá trị nào của m để A là tập con của B.
Vậy không tồn tại m.
Lời giải:
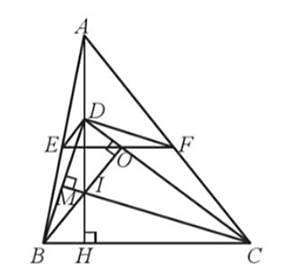
Kẻ BO vuông góc CD, CM vuông góc BD, BO cắt CM tại I
Suy ra: D là trực tâm của ∆BIC hay DI ⊥ BC
Mặt khác, AH ⊥ BC suy ra I, D, A thẳng hàng
Do = = 90° nên ED ⊥ DC, DF ⊥ DB
Ta có: ED ⊥ DC, BO ⊥ CD, I ∈ BO nên ED // BI
DF ⊥ DB, CM ⊥ BD, I ∈ CM nên DF // CI
Xét ∆ABI với DE // BI, ta có: (hệ quả của định lý Thalès)
Xét ∆ACI với DF // CI, ta có: (hệ quả của định lý Thalès)
Suy ra:
Xét tam giác ABC có nên EF // BC (định lý Thalès đảo).
Lời giải:
Ta có: 3x2 – 4xy + 2y2 = 3
⇔ x2 = 3 – 2y2 + 4xy – 2x2
⇔ x2 = 3 – 2(x – y)2
Thấy (x – y)2 ≥ 0 nên 3 – 2(x – y)2 ≤ 3 với mọi x, y
Suy ra: x2 ≤ 3 ⇒ x = 0 hoặc x = 1.
Vì x là số nguyên dương nên x = 1.
Thay vào 3x2 – 4xy + 2y2 = 3 ta được:
3 – 4y + 2y2 = 3
⇔ 2y(y – 2) = 0
⇔
M = x2022 + (y – 3)2022 = 12022 + (2 – 3)2022 = 1 + 1 = 2.
Vậy M = 2.
Đề bài: Cho . Chứng minh rằng A không phải là số tự nhiên.
Lời giải:
Để quy đồng ta sẽ chọn mẫu chung tích các thừa số nguyên tố chung và riêng (hay ta tìm BCNN của mẫu)
Ta chọn mẫu chung là 26.3.5.7.9.99
Gọi k1; k2; …; k100 là các thừa số phụ tương ứng, do đó A có dạng:
A =
Trong 100 phân số của tổng A chỉ có phân số duy nhất chứa 26 nên trong các thừa số phụ chỉ có k64 là số lẻ, còn lại các thừa số phụ đều là số chẵn.
Nên tử số không chia hết cho 2, trong khi mẫu số chia hết cho 2.
Do đó phân số A không phải là số tự nhiên.
Lời giải:
Làm vòng tay mỗi giờ được 10 ngàn đồng
Làm vòng đeo cổ mỗi giờ được: 40 : 3 ≈ 13 ngàn đồng
Vậy làm vòng đeo cổ có lợi hơn nên ưu tiên làm tối đa số vòng cổ trước.
Làm 4 vòng đeo cổ hết 4.6 = 24 giờ, bán được 4.80 = 320 ngàn đồng.
Để làm được ít nhất 400 ngàn đồng cần làm thêm vòng tay để thu về 80 ngàn đồng hay cần làm thêm 2 cái vòng tay
⇒ Cần thêm 2.4 = 8 giờ
Vậy cần tối thiểu: 24 + 8 = 32 giờ một tuần để An bán được ít nhất 400 ngàn đồng.
Lời giải:
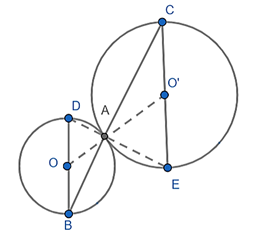
Có: (góc nội tiếp chắn nửa đường tròn (O))
(góc nội tiếp chắn nửa đường tròn (O'))
Suy ra:
Do đó: D, A, E thẳng hàng.
Ta có: tam giác AOD cân tại O vì OD = OA
Suy ra:
Tam giác O'AE cân tại O' vì O'A = O'E
⇒
Mà: (2 góc đối đỉnh) do đó BD // CE
Suy ra: (2 góc so le trong).
a, Chứng minh tứ giác EFCG là hình bình hành.
c, Cho biết BH = 4 cm, . Tính SABCD; SEFCG.
Lời giải:
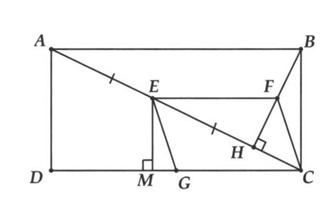
a) Vì E, F theo thứ tự là trung điểm của AH, BH nên EF là đường trung bình trong tam giác ABH
⇒ EF // AB và EF =
Vì AB // DG nên EF // DG
Xét tứ giác EFCG có: EF // DG và EF = DG
Nên EFCG là hình bình hành
b) Lại có: AB ⊥ BC mà EF // AB nên EF ⊥ BC
Mà BF ⊥ AC
Xét trong tam giác BEC có: EF ⊥ BC; BF ⊥ EC nên F là trực tâm của tam giác BEC
Suy ra: CF ⊥ BE (1)
Mà theo phần a có EFCG là hình bình hành nên: EG // CF (2)
Từ (1) và (2): EG ⊥ BE hay
c) Sử dụng tỉ số sinA trong tam giác vuông HAB ta có:
⇒
AC =
Lại có: AB2 = AH.AC ⇒ AH = AB2 : AC = 4
HC = AC – AH =
Mà AE = EH =
Suy ra: EC = HC + EH =
Kẻ EM vuông góc với CD tại M
Có (2 góc so le trong)
Ta có: sin
⇒ EM =
SABCD = AB.BC =
SEFCG = EM.EF = EM .
Đề bài: Chứng minh rằng biểu thức sau luôn dương với mọi giá trị của x: x2 + x + 1.
Lời giải:
Xét x2 + x + 1 = x2 +
Ta thấy nên
Vậy x2 + x + 1 luôn dương với mọi giá trị của x.
Đề bài: Cho tam giác ABC. Chứng minh điều kiện cần và đủ để ABC cân là
Lời giải:
Khi đó ta có: VP =
VT =
Dấu “=” xảy ra khi cos(A – B) = 1 hay , tức tam giác ABC cân tại C.
Lời giải:
Theo bài ra ta có: a = 4b + 35
Suy ra: b =
Mặt khác: số dư là 35 ⇒ số chia b > 35
Vậy 35 < b < 42 ⇒ b có thể là 36; 37; 38; 39; 40; 41
Khi đó a sẽ lần lượt là (a = b.4 + 35) = 179; 183; 187; 191; 195; 199.
Đề bài: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm; CH = 16cm.
Lời giải:
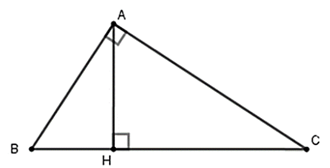
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.BC = 9.25 = 225
Suy ra: AB = 15cm
AC2 = CH.BC = 16.25 = 400
Suy ra: AC = 20cm
Lại có: AH.BC = AB.AC ⇒ AH = cm.
Lời giải:
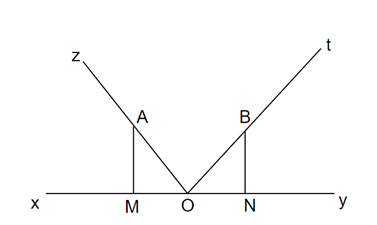
a) Ta có:
Mà
⇒
Lại có:
⇒
Xét ∆OAM và ∆BON có:
OA = OB
⇒ ∆OAM = ∆BON (g.c.g)
b) Có ∆OAM = ∆BON (phần a) nên MA = ON và OM = BN
Xét: AM + BN = ON + OM = MN
Vậy MN = AM + BN.
Lời giải:
Gọi a là độ dài cạnh tam giác đều ABC.
Vì E thuộc CN nên tồn tại x, y sao cho x + y = 1 (1)
Với
Vì E thuộc AM nên
Từ (1) và (2) suy ra:
Vậy
Mặt khác:
Khi đó:
=
Vậy BE vuông góc CN hay EB vuông góc với EC.
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Tổng hợp các đề đọc - hiểu có đáp án chi tiết
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)
