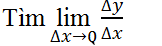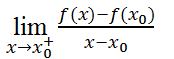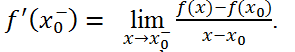Nội dung bài viết

    Xem thêm

    Đạo hàm của 3^x

    Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

    1 93 01/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Đề bài: Đạo hàm của 3x

    *Lời giải

    Đạo hàm của 3x là 3x.lnx

    *Phương pháp giải

    Sử dụng bảng công thức tính đạo hàm

    *Lý thuyết

    1. Định nghĩa

    Giới hạn nếu có của tỉ số giữa số gia của hàm số và số gia của đối số tại x_0, khi số gia của đối số tiến dần tới 0, được gọi là đạo hàm của hàm số y=f(x) tại điểm x_0.

    Cho hàm số y=f(x) xác định trên (a;b) và x_0\in(a;b):
    f'({x_0})=\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) – f({x_0})}}{{x – {x_0}}}=\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} (\Delta x = x – x_0, \Delta y = f(x_0 + \Delta x) – f(x_0)
    Nếu hàm số y=f(x) có đạo hàm tại x_0 thì nó liên tục tại điểm đó.

    2. Cách tính đạo hàm bằng định nghĩa

    Quy tắc tính đạo hàm bằng định nghĩa:

    + Bước 1: Giả sử ∆x là số gia của đối số tại x0; tính :

    ∆y= f( x0+ ∆x)- f( x0) .

    + Bước 2: Lập tỉ số ∆y/∆x.

    + Bước 3:

    Tổng hợp các công thức tính đạo hàm chi tiết

    3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

    * Định lí: Nếu hàm số y= f( x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.

    * Chú ý:

    + Nếu hàm số y= f(x) gián đoạn tại x0 thì hàm số không có đạo hàm tại điểm đó.

    + Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

    4. Đạo hàm một bên, Đạo hàm trên khoảng, trên đoạn

    a. Đạo hàm bên trái, bên phải

    + Nếu tồn tại giới hạn( hữu hạn) bên phảiTổng hợp các công thức tính đạo hàm chi tiết

    ta gọi giới hạn đó là đạo hàm bên phải của hàm số y= f(x) tại x=x0 và kí hiệu f'(x0+)

    + Tương tự; đạo hàm bên trái của hàm số làTổng hợp các công thức tính đạo hàm chi tiết

    Hệ quả : Hàm số y= f(x) có đạo hàm tại x0 khi và chỉ khi tồn tại f'(x0+) và f;(x0-) đồng thời f' (x0+ )=f'(x0-) .

    b. Đạo hàm trên khoảng, trên đoạn

    Hàm số y=f(x) có đạo hàm trên (a;b) nếu nó có đạo hàm tại mọi điểm thuộc (a; b).

    Hàm số y= f(x) có đạo hàm trên[a;b] nếu nó có đạo hàm tại mọi điểm thuộc khoảng (a; b) đồng thời tồn tại đạo hàm trái tại x= b và đạo hàm phải tại x= a.

    5. Ý nghĩa hình học của đạo hàm

    Định lí: Đạo hàm của hàm số y= f(x) taị điểm x=x0 là hệ số góc của tiếp tuyến M0T của đồ thị hàm số y= f( x) tại điểm M0(x0; f(x0)).

    Định lí: Phương trình tiếp tuyến của đồ thị hàm số y= f(x) tại điểm M0(x0; f(x0)) là:

    y – y0= f’(x0) ( x- x0)

    trong đó y0= f( x0)

    6. Ý nghĩa vật lí của đạo hàm

    a. Vận tốc tức thời.

    Xét chuyển động thẳng xác định bởi phương trình: s= s(t); với s= s(t) là một hàm số có đạo hàm. Vận tốc tức thời tại thời điểm t0 là đạo hàm của hàm số s= s(t) tại t0:

    v(t0) = s’(t0)

    b. Cường độ tức thời.

    Nếu điện lượng Q truyền trong dây dẫn là một hàm số của thời gian: Q= Q(t) ( là hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm t0 là đạo hàm của hàm số Q= Q(t) tại t0:

    I(t0)= Q’(t0) .

    Xem thêm

    Tổng hợp công thức đạo hàm

    50 bài tập về Đạo hàm của hàm số lượng giác

    Tham khảo các loạt bài Toán khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 93 01/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: