1500 câu hỏi ôn tập Toán (Phần 8)

Câu 1: Cho đường thẳng d và hai điểm A, B nằm cùng phía với d. Tìm điểm M trên d sao cho MA + MB đạt giá trị nhỏ nhất ?

Lời giải:

- Tìm điểm A’ đối xứng với A qua d

- Nối A’B cắt d tại M. M chính là điểm cần tìm.

- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA = MA’.

Do đó : MA + MB = MA’ + MB = A’B .

- Giả sử tồn tại M’ khác M thuộc d thì : M’A + M’B = M’A’ + M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’ 

Câu 2: Cho một đường thẳng d và hai điểm phân biệt A, B không thuộc d.

Tìm điểm C thuộc d sao cho A, B, C thẳng hàng. Khi nào không thể tìm được điểm C như vậy?

Lời giải:

Vì hai điểm A, B phân biệt nên có thể vẽ được đường thẳng d’ đi qua hai điểm đó.

Hai điểm A, B không thuộc d thì d’ không trùng với d

Theo đầu bài, ta cần ba điểm A, B, C thẳng hàng nghĩa là C phải nằm trên đường thẳng d’ mà C phải thuộc vào d. Do đó C là giao điểm của hai đường thẳng d và đường thẳng d’.

+) Nếu d’ và d không có giao điểm nghĩa là d’ song song với d thì không thể tìm được điểm C như vậy.

Câu 3: Trong mặt phẳng cho 10 điểm phân biệt  A₁, A₂,... A₁₀ trong đó có 4 điểm  A₁, A₂, A₃, A₄ thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh được lấy trong 10 điểm trên là

A. 116 tam giác

B. 80 tam giác

C. 96 tam giác

D. 60 tam giác

Lời giải:

Chọn A

Số tam giác được tạo thành từ 10 điểm là $C_{10}^3$ tam giác

Do 4 điểm A₁, A₂, A₃, A₄ thẳng hàng nên số tam giác mất đi là $C_4^3$

Vậy số tam giác thỏa mãn yêu cầu Đề bài: $C_{10}^3-C_4^3=116$ là tam giác

Câu 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất 

$\text{y = 3sin}\left(\text{3x + }\frac{\text{π}}{\text{6}}\right)\text{ + 4cos}\left(\text{3x + }\frac{\text{π}}{\text{6}}\right)$

Lời giải:

$\text{y = 5}\left[\frac{\text{3}}{\text{5}}\text{sin}\left(\text{3x + }\frac{\text{π}}{\text{6}}\right)\text{ + }\frac{\text{4}}{\text{5}}\text{cos}\left(\text{3x + }\frac{\text{π}}{\text{6}}\right)\right]$

$\text{y = 5 . sin}\left(\text{3x + }\frac{\text{π}}{\text{6}}\text{ + a}\right)$ với $\text{cosa = }\frac{\text{3}}{\text{5}}$

Do $-1\le \text{sin}\left(\text{3x + }\frac{\text{π}}{\text{6}}\text{ + a}\right)\le 1$

$\Rightarrow \text{-5}\le \text{y}\le \text{5}$

Câu 5: Hưởng ứng phong trào quyên góp sách giáo khoa cũ giúp đỡ học sinh có hoàn cảnh khó khắn, ba lớp 7A, 7B, 7C đã quyên góp số sách lần lượt với tỉ lệ 3; 4; 5. Tính số sách giáo khoa của mỗi lớp quyên góp, biết số sách quyên góp của lớp 7C hơn lớp 7A là 22 quyển.

Lời giải:

Gọi số sách quyên góp của 3 lớp 7A, 7B, 7C lần lượt là a (quyển), b (quyển), c (quyển)

(điều kiện

Theo đầu bài ta có: $\frac{\text{a}}{\text{3}}\text{ = }\frac{\text{b}}{\text{4}}\text{ = }\frac{\text{c}}{\text{5}}$ và c – a = 22

Áp dụng tính chất: $\frac{\text{a}}{\text{b}}\text{ = }\frac{\text{c}}{\text{d}}\text{ = }\frac{\text{a – c}}{\text{b – d}}$

Ta có: $\frac{\text{a}}{\text{3}}\text{ = }\frac{\text{c}}{\text{5}}\text{ = }\frac{\text{c – a}}{\text{5 – 3}}\text{ = }\frac{\text{22}}{\text{2}}\text{ = 11}$

$\frac{\text{a}}{\text{3}}\text{ = 11}\Rightarrow \text{a = 3 . 11 = 33; }\frac{\text{c}}{\text{5}}\text{ = 5 . 11 = 55}$

Ta có: $\frac{\text{a}}{\text{3}}\text{ = }\frac{\text{b}}{\text{4}}\Rightarrow \frac{\text{33}}{\text{3}}\text{ = }\frac{\text{b}}{\text{4}}\Rightarrow \text{b = }\frac{\text{33 . 4}}{\text{3}}\text{ = 44}$

Vậy số sách quyên góp của lớp 7A, 7B, 7C lần lượt là:

33 (quyển), 44 (quyển), 55 (quyển).

Câu 6: cho các số hữu tỉ là a, b, c khác 0 thỏa mãn : $\frac{\text{a + b - c}}{\text{c}}\text{ = }\frac{\text{a - b + c}}{\text{b}}\text{ = }\frac{\text{-a + b + c}}{\text{a}}$. Tính giá trị của biểu thức $\text{M = }\frac{\left(\text{a + b}\right)\left(\text{b + c}\right)\left(\text{c + a}\right)}{\text{abc}}$

Lời giải:

Theo bài ra, ta có:

$\frac{\text{a + b - c}}{\text{c}}\text{ = }\frac{\text{a - b + c}}{\text{b}}\text{ = }\frac{\text{-a + b + c}}{\text{a}}$

áp dụng tính chất ta có:

$$\begin{gathered} \frac{\text{a + b - c}}{\text{c}}\text{ = }\frac{\text{a - b + c}}{\text{b}}\text{ = }\frac{\text{-a + b + c}}{\text{a}} \\ \text{= }\frac{\text{a + b - c + a - b + c + -a + b + c}}{\text{c + b + a}}\text{ = }\frac{\text{a + b + c}}{\text{c + b + a}}\text{ = 1} \end{gathered}$$

$$\begin{gathered} \Rightarrow \text{ a + b - c = c }\Rightarrow \text{ a + b = 2c }\left(\text{1}\right) \\ \Rightarrow \text{ a - b + c = b }\Rightarrow \text{ a + c = 2b }\left(\text{2}\right) \\ \Rightarrow \text{ -a + b + c = a }\Rightarrow \text{ b + c = 2a }\left(\text{3}\right) \end{gathered}$$

thay 1, 2 và 3 vào biểu thức M ta có:

$\text{M = }\frac{\text{2c . 2a . 2b}}{\text{abc}}\text{ = }\frac{\text{8abc}}{\text{abc}}\text{ = 8}$

Vậy M = 8

Câu 7: Cho biết $\frac{\text{x}}{\text{y}}\text{ = }\frac{\text{7}}{\text{10}}\text{ ; }\frac{\text{y}}{\text{z }}\text{ = }\frac{\text{10 }}{\text{13 }}$  và x + y + z =120 .Tìm x,y,z

Lời giải:

$\begin{array}{l}\frac{x}{y}=\frac{7}{10}\Rightarrow \frac{x}{7}=\frac{y}{10}\\ \frac{y}{z}=\frac{10}{13}\Rightarrow \frac{y}{10}=\frac{z}{13}\\ \Rightarrow \frac{x}{7}=\frac{y}{10}=\frac{z}{13}\end{array}$

Theo tính chất dãy tỉ số bằng nhau ta có:

$\begin{array}{l}\frac{x}{7}=\frac{y}{10}=\frac{z}{13}=\frac{x+y+z}{7+10+13}=\frac{120}{30}=4\\ \Rightarrow x=7.4=28\\ y=10.4=40\\ z=13.4=52\end{array}$

Vậy $\left(\text{x; y; z}\right)\text{ = }\left(\text{28; 40; 52}\right)$

Câu 8: Chứng minh đẳng thức

tan²x - sin²x = tan²x . sin²x

Lời giải:

$$\begin{gathered} {\text{tan}}^{\text{2}}{\text{x - sin}}^{\text{2}}\text{x = }\frac{{\text{sin}}^{\text{2}}\text{x}}{{\text{cos}}^{\text{2}}\text{x}}{\text{ - sin}}^{\text{2}}{\text{x = sin}}^{\text{2}}\text{x . }\left(\frac{\text{1}}{{\text{cos}}^{\text{2}}\text{x}}\text{ - 1}\right) \\ {\text{= sin}}^{\text{2}}\text{x . }\frac{{\text{sin}}^{\text{2}}\text{x}}{{\text{cos}}^{\text{2}}\text{x}}{\text{ = tan}}^{\text{2}}{\text{x . sin}}^{\text{2}}\text{x} \end{gathered}$$

Câu 9: Cho hai điểm A(x₁; y₁) và B(x₂; y₂) với $x_1\ne x_2;y_1\ne y_2$. Chứng minh rằng nếu đường thẳng y = ax + b đi qua A và B thì $\frac{{\text{y - y}}_{\text{1}}}{{\text{y}}_{\text{2}}{\text{ - y}}_{\text{1}}}\text{ = }\frac{{\text{x - x}}_{\text{1}}}{{\text{x}}_{\text{2}}{\text{ - x}}_{\text{1}}}$

Lời giải:

Vì đường thẳng đi qua A nên tọa độ điểm A thỏa mãn: y₁ = ax₁ + b (1).

Đường thẳng đi qua B nên tọa độ điểm B thỏa mãn: y₂ = ax₂ + b (2)

Trừ vế với vế của (1) cho (2) ta được: $a=\frac{y_1-y_2}{x_1-x_2},b=y_1-\frac{y_1-y_2}{x_1-x_2}.x_1=\frac{y_1{x}_2-y_2{x}_1}{x_1-x_2}$

Do đó ta có: $\frac{{\text{y - y}}_{\text{1}}}{{\text{y}}_{\text{2}}{\text{ - y}}_{\text{1}}}\text{ = }\frac{{\text{x - x}}_{\text{1}}}{{\text{x}}_{\text{2}}{\text{ - x}}_{\text{1}}}$ .

Câu 10: Cho hàm số y = -x + 5 có đồ thị là (d₁)

$y=\frac{x}{2}-1$ có đồ thị là (d₂)

A) Vẽ (d₁), (d₂) trên cùng mặt phẳng tọa độ

B) Tìm tọa độ giao điểm của (d₁), (d₂)

Lời giải:

y = -x + 5

Cho $\text{x = 0 }\Rightarrow \text{ y = 5 }\Rightarrow$  dths đi qua A(0; 5)

cho  $\text{y = 0 }\Rightarrow \text{ x = 5 }\Rightarrow$  dths đi qua B(5; 0)

Nối A; B ta được dths y = -x + 5

$y=\frac{x}{2}-1$

cho $\text{x = 0 }\Rightarrow \text{ y = -1 }\Rightarrow$  dths đi qua C(0; -1)

cho $\text{x = 2 }\Rightarrow \text{ y = 0 }\Rightarrow$  dths đi qua D(2; 0)

Nối C; D ta được dths cần tìm

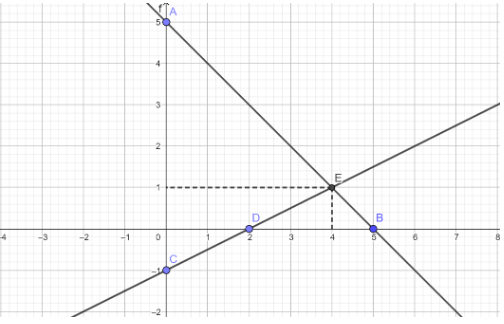
b) Từ dths ta thấy tọa độ giao điểm của 2 hàm số là E(4; 1)

Câu 11: Gọi d₁ là đồ thị hàm số y = −(2m − 2)x + 4m và d₂ là đồ thị hàm số y = 4x – 1 . Xác định giá trị của m để M(1; 3) là giao điểm của d₁ và d₂.

A. $m=\frac{1}{2}$

B. $m=-\frac{1}{2}$

C. m = 2

D. m = −2

Lời giải:

Nhận thấy $\text{M }\in {\text{d}}_{\text{2}}$

Ta thay tọa độ điểm M vào phương trình d₁ được phương trình

$\text{3 = -}\left(\text{2m - 2}\right)\text{ . 1 + 4m}\iff \text{m = }\frac{\text{1}}{\text{2}}$

Vậy $\text{m = }\frac{\text{1}}{\text{2}}$

Đáp án cần chọn là: A.

Câu 12: Cho $\Delta ABC$ cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?

A. 3 cm

B. 6cm

C. 9cm

D. 12cm

Lời giải:

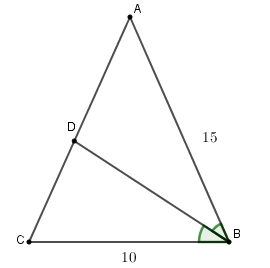
Vì BD là đường phân giác của $\widehat{\text{ABC}}$ nên: $\frac{\text{AD}}{\text{DC}}\text{ = }\frac{\text{AB}}{\text{BC}}$

Suy ra: $\frac{\text{AD}}{\text{DC + AD}}\text{ = }\frac{\text{AB}}{\text{BC + AB}}$ (theo tính chất dãy tỉ số bằng nhau) .

$\Rightarrow \frac{\text{AD}}{\text{AC}}\text{ = }\frac{\text{AB}}{\text{BC + AB}}$

Mà tam giác ABC cân tại A nên AC = AB = 15cm

Đáp án: C

Câu 13: Cho $\Delta ABC$ cân tại A . Tia giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E. Chứng minh cân.

Lời giải:

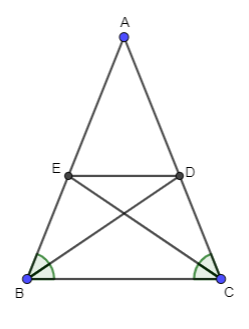
$\Delta ABC$ cân tại A nên $\widehat{ABC}=\widehat{ACB}$ (t/c tam giác cân)

$\Rightarrow \frac{\widehat{\text{ABC}}}{\text{2}}\text{ = }\frac{\widehat{\text{ACB}}}{\text{2}}$

Mà $\widehat{\text{ABD}}\text{ = }\widehat{\text{CBD}}\text{ = }\frac{\widehat{\text{ABC}}}{\text{2}}$

$\widehat{\text{ACE}}\text{ = }\widehat{\text{BCE}}\text{ = }\frac{\widehat{\text{ACB}}}{\text{2}}$

Nên $\widehat{\text{ABD}}\text{ = }\widehat{\text{CBD}}\text{ = }\widehat{\text{ACE}}\text{ = }\widehat{\text{BCE}}$

Xét $\Delta EBC$ và $\Delta DCB$ có:

$\widehat{\text{EBC}}\text{ = }\widehat{\text{DCB}}$ (cmt)

BC là cạnh chung

$\widehat{\text{ECB}}\text{ = }\widehat{\text{DBC}}$ (cmt)

Do đó, $\Delta EBC=\Delta DCB$  (g.c.g)

$\Rightarrow$ BE = CD (2 cạnh tương ứng)

Mà AB = AC (gt) nên AB - BE = AC - CD

$\Rightarrow$ AE = AD

$\Rightarrow \Delta AED$ cân tại A (đpcm)

Câu 14: Trong không gian với hệ tọa độ Oxyz, cho với A(1; 0; 0), B(3; 2; 4), C(0; 5; 4). Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $\left|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\right|$ nhỏ nhất.

A. M(1; 3; 0).

B. M(1; −3; 0).

C. M(3; 1; 0).

D. M(2; 6; 0).

Lời giải:

+ Ta tìm điểm I(a; b; c) thỏa mãn

$\overrightarrow{\text{IA}}\text{ + }\overrightarrow{\text{IB}}\text{ + 2}\overrightarrow{\text{IC}}$

Hay $\left\{\begin{array}{c}\text{1 - a + 3 - a - 2a = 0}\\ \text{-b + 2 - b + 2(5 - b) = 0}\\ \text{-c + 4 - c + 2(4 - c) = 0}\end{array}\right.\iff \left\{\begin{array}{c}a=1\\ b=3\\ c=3\end{array}\right.\Rightarrow \text{I}\left(\text{1; 3; 3}\right)$

+ Khi đó: $\left|\overrightarrow{\text{MA}}\text{ + }\overrightarrow{\text{MB}}\text{ + 2}\overrightarrow{\text{MC}}\right|\text{ = }\left|\text{4}\overrightarrow{\text{MI}}\right|\ge \text{4IH}$

với H là hình chiếu của I trên  (Oxy) và H(1; 3; 0)

Do đó $\text{min}\left|\overrightarrow{\text{MA}}\text{ + }\overrightarrow{\text{MB}}\text{ + 2}\overrightarrow{\text{MC}}\right|\text{ = 4IH = 12}$

khi  $H\equiv M$ hay M(1;3;0)

Đáp án cần chọn là: A

Câu 15: Cho $\Delta ABC$ vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.

a) Chứng minh BE = CD, AD = AE.

b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.

Lời giải:

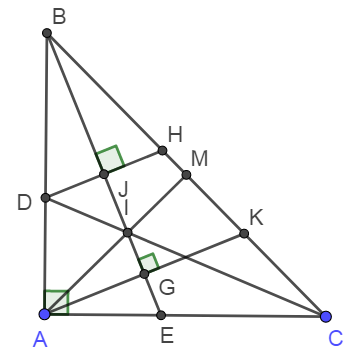
a) Do tam giác ABC vuông cân nên $\widehat{\text{ABC}}\text{ =}\widehat{\text{ ACB}}\Rightarrow \widehat{\text{ABE}}\text{ = }\widehat{\text{ACD}}$

Xét tam giác vuông ABE và tam giác vuông ACD có:

AB = AC (gt)

$\widehat{\text{ABE}}\text{ = }\widehat{\text{ACD}}$

$\Rightarrow \text{ΔABE = ΔACD}$ (Cạnh góc vuông - góc nhọn kề)

$\Rightarrow$ BE = CD; AE = AD

b) I là giao điểm của hai tia phân giác góc B và góc C của nên AI cũng là phân giác góc A.

Do $\Delta ABC$  cân tại A nên AI là phân giác đồng thời là đường cao và trung tuyến.

Vậy thì $\widehat{\text{AMC}}{\text{ = 90}}^{\text{o}}\text{; BM = MC = AM}$

Từ đó suy ra $\Delta AMC$ vuông cân tại M.

c) Gọi giao điểm của DH, AK với BE lần lượt là J và G.

Do DH và AK cùng vuông góc với BE nên ta có

$\text{ΔBDJ = ΔBHJ; ΔBAG = ΔBKG}\Rightarrow \text{BD = BH; BA = BK}$

$\Rightarrow HK=AD$

Mà AD = AE nên HK = AE.    (1)

Do $\Delta BAK$ cân tại B, có ${}^{\text{o}}\Rightarrow \widehat{\text{BAK}}\text{ = }\frac{{\text{180}}^{\text{o}}{\text{ - 45}}^{\text{o}}}{\text{2}}{\text{ = 67,5}}^{\text{o}}$

$\Rightarrow \widehat{\text{GAE}}{\text{ = 90}}^{\text{o}}{\text{ - 67,5}}^{\text{o}}{\text{ = 22,5}}^{\text{o}}\text{ = }\frac{\widehat{\text{IAE}}}{\text{2}}$

Suy ra AG là phân giác góc IAE.

Từ đó ta có $\widehat{\text{KAC}}\text{ = }\widehat{\text{ICA}}\left({\text{ = 22,5}}^{\text{o}}\right)$

$\Rightarrow \text{ΔAKC = ΔCIA}\left(\text{g - c - g}\right)\Rightarrow \text{KC = IA}$

Lại có $\Delta AIE$ có AG là phân giác đồng thời đường cao nên nó là tam giác cân, hay AI = AE. Suy ra KC = AE  (2)

Từ (1) và (2) suy ra HK = KC.

Câu 16: $3\frac{9}{100}$  viết dưới dạng số thập phân là:

A. 3,09

B. 3,900

C. 3,009

D. 3,90

Lời giải:

Chọn A

$3\frac{9}{100}=\mathrm{3,09}$

Vậy  $3\frac{9}{100}$ được viết dưới dạng số thập phân là 3,09

Câu 17: Một nhóm học sinh gồm 5 nam và 3 nữ. Có bao nhiêu cách chọn 5 người để làm ban đại diện sao cho có đúng ba nam?

A. 20

B. 15

C. 30

D. 45

Lời giải:

Chọn 3 nam trong 5 nam là số tổ hợp chập 3 của 5 phần tử: $C_5^3$

Chọn 2 nữ trong 3 nữ là số tổ hợp chập 2 của 3 phần tử: $C_3^2$

Số cách chọn thỏa mãn Đề bài: là ${\text{C}}_{\text{5}}^{\text{3}}{\text{ . C}}_{\text{3}}^{\text{2}}\text{ = 30}$

Câu 18: Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.

a) Chứng minh $\text{ΔABH = ΔACH}$

b) Chứng minh AH ⊥ BC

c) Vẽ $\text{HD }\perp \text{AB (D }\in \text{AB)}$  và $HE\perp AC(E\in AC)$ . Chứng minh: DE // BC

Lời giải:

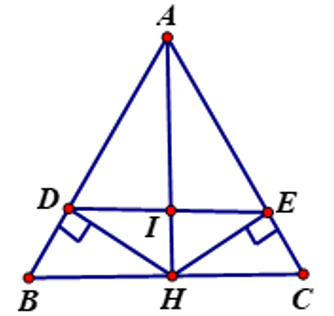
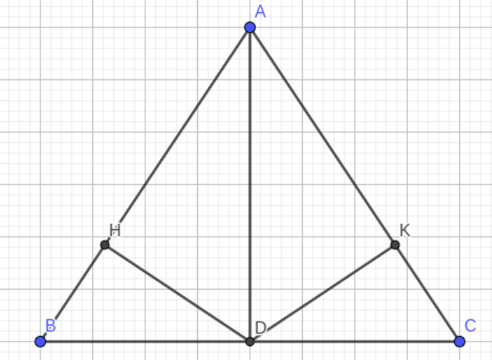
Câu 19: Cho $\text{ΔABC}$ có AB = AC. Tia phân giác của góc A cắt BC tại D.

a) Chứng minh tam giác ABD bằng tam giác ADC.

b) Kẻ $DH\perp AB$  (h tập hợp AB ) $DK\perp AC$ ( $K\in AC$) Chứng minh BH = CK.

c) Biết $\hat{A} = 4\hat{B}$  tính số đo các góc của tam giác $\text{ΔABC}$

Lời giải:

a)Ta có: $\text{AB = AC, }\widehat{\text{BAD}}\text{ = }\widehat{\text{DAC}}\to \text{ΔABD = ΔACD(c . g . c)}$

b)Từ câu a $\Rightarrow$ DB = DC

Mà $\widehat{\text{DHB}}\text{ =}\widehat{\text{ DKC}}{\text{ = 90}}^{\text{o}}\text{, }\widehat{\text{ABC}}\text{ = }\widehat{\text{ACB}}$

$\Rightarrow \text{ΔDHB = ΔDKC}$ (cạnh huyền – góc nhọn)

$\Rightarrow \text{BH = CK}$

c) Ta có : AB = AC suy ra tam giác ABC cân tại A

$\Rightarrow \hat{B}=\hat{C}$

Mà $\hat{A} = 4\hat{B}$

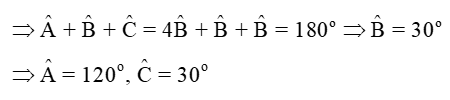
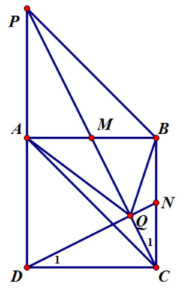
Câu 20: Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA

a) Cm: APBC là hình bình hành và BCDP là hình thang vuông

b) CM: 2Sbcdp = 3Sapbc

c) Gọi N là trung điểm BC, Q là giao điểm DN và CM. Cm: AQ = AB

Lời giải:

a) Ta có: $\widehat{{\text{M}}_{\text{1}}}\text{ = }\widehat{{\text{M}}_{\text{2}}}$ (2 góc đổi đỉnh)

$\Rightarrow \text{ΔAMP = ΔBMC(g . c . g)}\Rightarrow \text{MP = MC}$

Xét tứ giác APBC có AB và CP là 2 đường chéo nhau tại trung điểm mỗi đường nên APBC là hình bình hành.
Vì APBC là hình bình hành nên $\text{BC // AP}\Rightarrow \text{BC // DP}$  mà $\text{BC }\perp \text{CD}$

$\Rightarrow$ BCDP là hình thang vuông (Điều phải chứng minh).
b) Nhận xét: ${\text{S}}_{\text{ADC}}{\text{ = S}}_{\text{ABC}}{\text{ = S}}_{\text{ABP}}$  và đặt ${\text{S}}_{\text{ADC}}{\text{ = S}}_{\text{ABC}}{\text{ = S}}_{\text{ABP}}\text{ = a}$

Khi đó: ${\text{2S}}_{\text{BCDP}}{\text{ = 2 . 3a = 6a; 3S}}_{\text{APBC}}\text{ = 3 . 2a = 6a}$

Suy ra đpcm.

c) Vì M là trung điểm của AB nên $\text{BM = }\frac{\text{1}}{\text{2}}\text{AB}$

Vì N là trung điểm của BC nên $\text{CN = }\frac{\text{1}}{\text{2}}\text{BC}$ mà

$\text{AB = BC}\Rightarrow \text{BM = CN}\Rightarrow \text{ΔCBM = ΔDCN(c . g . c)}\Rightarrow \widehat{{\text{C}}_{\text{1}}}\text{ = }\widehat{{\text{D}}_{\text{1}}}$

mà $\Delta DCN$ vuông tại C nên

$\widehat{{\text{D}}_{\text{1}}}\text{ + }\widehat{{\text{N}}_{\text{1}}}{\text{ = 90}}^{\text{o}}\Rightarrow \widehat{{\text{C}}_{\text{1}}}\text{ + }\widehat{{\text{N}}_{\text{1}}}{\text{ = 90}}^{\text{o}}\Rightarrow \widehat{\text{CQN}}{\text{ = 90}}^{\text{o}}$

$\Rightarrow \Delta PDQ$ vuông tại Q.
Xét vuông tại Q, có QA là đường trung tuyến ứng với cạnh huyền

$\Rightarrow \text{QA = }\frac{\text{1}}{\text{2}}\text{PD = AD}$  mà $\text{AD = AB}\Rightarrow \text{AQ = AB}$  (Điều phải chứng minh). 

Câu 21: Cho phương trình x² – mx + m – 3 = 0.

a) Chứng minh rằng phương trình đã cho luôn có 2 nghiệm phân biệt x₁, x₂.

b) Tìm hệ thức liên hệ giữa 2 nghiệm x₁, x₂ mà không phụ thuộc vào m.

Lời giải:

a) ∆ = (–m)² – 4(m – 3) = m² – 4m + 12 = (m – 2)² + 8.

Ta có (m – 2)² ≥ 0, ∀m ∈ ℝ.

⇔ (m – 2)² + 8 ≥ 8 > 0, ∀m ∈ ℝ.

⇔ ∆ > 0, ∀m ∈ ℝ.

Vậy phương trình đã cho luôn có 2 nghiệm phân biệt x₁, x₂.

b) Theo Viet: S = x₁ + x₂ = m và P = x₁x₂ = m – 3.

Suy ra x₁ + x₂ – x₁x₂ = m – m + 3 = 3.

Vậy hệ thức cần tìm là x₁ + x₂ – x₁x₂ = 3.

Câu 22: Cho phương trình bậc hai ẩn x, tham số m: x² + mx + m + 3 = 0.

Tìm m để phương trình có 2 nghiệm trái dấu.

Lời giải:

Phương trình đã cho có 2 nghiệm trái dấu ⇔ P < 0.

⇔ m + 3 < 0.

⇔ m < –3.

Vậy m < –3 thỏa mãn yêu cầu bài toán.

Câu 23: Tập hợp các số tự nhiên là gì?

Lời giải:

⦁ Tập hợp các số tự nhiên được kí hiệu là ℕ.

Ta có ℕ = {0; 1; 2; 3;…}.

⦁ Tập hợp các số tự nhiên khác 0 được kí hiệu là ℕ*.

Ta có ℕ* = {1; 2; 3;…}.

Câu 24: Cho f(x) = ax² + bx + c. Tìm điều kiện của tham số m để f(x) < 0 với mọi x thuộc ℝ.

Lời giải:

Cần xét hai trường hợp:

Trường hợp 1: a = 0.

Trường hợp 2: a ≠ 0.

Ta có $f\left(x\right)<\mathrm{0,}\forall x\in ℝ\iff \left\{\begin{array}{l}a<0\\ \Delta <0\end{array}\right.$  (hoặc $f\left(x\right)<\mathrm{0,}\forall x\in ℝ\iff \left\{\begin{array}{l}a<0\\ {\Delta }^{\text{'}}<0\end{array}\right.$ ).

Câu 25: Phân tích đa thức thành nhân tử:

a) 3x² – 6xy + 3y² – 12;

b) 4x² – 4x + 1 – 9y²;

c) 9x² – 6x + 1 – 16y².

Lời giải:

a) 3x² – 6xy + 3y² – 12

= 3(x² – 2xy + y² – 4)

= 3[(x – y)² – 2²]

= 3(x – y + 2)(x – y – 2).

b) 4x² – 4x + 1 – 9y²

= (2x – 1)² – (3y)²

= (2x – 1 – 3y)(2x – 1 + 3y).

c) 9x² – 6x + 1 – 16y²

= (3x – 1)² – (4y)²

= (3x – 1 – 4y)(3x – 1 + 4y).

Câu 26: Phân tích đa thức sau thành nhân tử:

a) 3x² + 3y² – 6xy – 12;

b) x⁴ + x³ + 2x² + x + 1.

Lời giải:

a) 3x² + 3y² – 6xy – 12

= 3(x² – 2xy + y² – 4)

= 3[(x – y)² – 2²]

= 3(x – y + 2)(x – y – 2).

b) x⁴ + x³ + 2x² + x + 1

= (x⁴ + 2x² + 1) + (x³ + x)

= (x² + 1)² + x(x² + 1)

= (x² + 1)(x² + 1 + x).

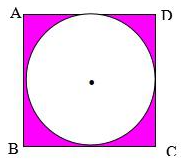
Câu 27: Hình vẽ bên là một hình vuông ABCD có chu vi 48 dm. Tính diện tích phần tô đậm?

Lời giải:

Độ dài cạnh của hình vuông ABCD là: 48 : 4 = 12 (dm).

Diện tích của hình vuông ABCD là: 12.12 = 144 (dm²).

Bán kính hình tròn là: 12 : 2 = 6 (dm).

Diện tích hình tròn là: 6.6.3,14 = 113,04 (dm²).

Diện tích phần tô đậm là: 144 – 113,04 = 30,96 (dm²).

Đáp số: 30,96 dm².

Câu 28: Tính bằng cách hợp lí: A = (–30) + (–29) + … + 48 + 49 + 50.

Lời giải:

A = (–30) + (–29) + … + 48 + 49 + 50

= [(–30) + 30] + [(–29) + 29] + … + [(–1) + 1] + 31 + 32 + … + 50

= 0 + 0 + … + 0 + 31 + 32 + … + 50

$=\left(\frac{50-31}{1}+1\right):2\left(31+50\right)=810$.

Câu 29: Tìm x, biết: (3x + 2)² – (1 – 2x)² = 0.

Lời giải:

(3x + 2)² – (1 – 2x)² = 0

⇔ (3x + 2 – 1 + 2x)(3x + 2 + 1 – 2x) = 0

⇔ (5x + 1)(x + 3) = 0

⇔ 5x + 1 = 0 hoặc x + 3 = 0

⇔ $x=-\frac{1}{5}$  hoặc x = –3.

Vậy $x\in \left\{-\frac{1}{5};-3\right\}$ .

Câu 30: Tìm x, y là số nguyên, biết:

a) x.y = 11;

b) (2x + 1)(3y – 2) = 12;

c) 1 + 2 + 3 + … + x = 55;

d) 6 ⋮ (x – 1);

e) (2x + 1)³ = 27;

f) 2^x.16 = 128.

Lời giải:

a) x.y = 11 = 1.11.

$\Rightarrow \left\{\begin{array}{l}x=1\\ y=11\end{array}\right.$ hoặc $\left\{\begin{array}{l}x=11\\ y=1\end{array}\right.$

Vậy (x; y) ∈ {(1; 11), (11; 1)}.

b) (2x + 1)(3y – 2) = 12

Ta có {2x + 1; 3y – 2} ∈ Ư(12).

Ư(12) ∈ {1; 2; 3; 4; 6; 12}.

Ta có bảng sau:

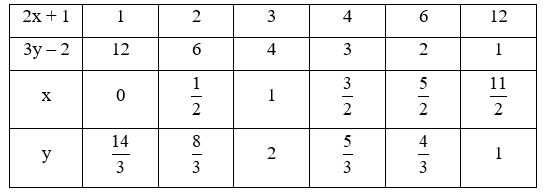
Mà x, y là số nguyên nên $\left(x;y\right)=\left(1;2\right)$

Vậy $\left(x;y\right)=\left(1;2\right)$ .

c) Từ 1 đến x có: (x – 1) : 1 + 1 = x số hạng.

Ta có 1 + 2 + 3 + … + x = 55

⇔ (x + 1) . x : 2 = 55

⇔ (x + 1) . x = 110

⇔ x² + x – 110 = 0

⇔ x² – 10x + 11x – 110 = 0

⇔ x(x – 10) + 11(x – 10) = 0

⇔ (x – 10)(x + 11) = 0

⇔ x – 10 = 0 hoặc x + 11 = 0

⇔ x = 10 hoặc x = –11.

Vậy x ∈ {10; –11}.

d) Ta có 6 chia hết cho (x – 1).

Suy ra x – 1 ∈ {1; 2; 3; 6}.

Vậy x ∈ {2; 3; 4; 7}.

e) (2x + 1)³ = 27

⇔ (2x + 1)³ = 3³

⇔ 2x + 1 = 3

⇔ 2x = 2

⇔ x = 1.

Vậy x ∈ {1}.

f) 2^x.16 = 128

⇔ 2^x = 8

⇔ 2^x = 2³

⇔ x = 3.

Vậy x ∈ {3}.

Câu 31: So sánh: A = 2017.2019 và B = 2018².

Lời giải:

Ta có: A − B = 2017.2019 − 2018²

= 2017.(2018 + 1) − 2018.(2017 + 1)

= 2017.2018 + 2017 − 2018.2017 − 2018

= 2017 − 2018 = −1 < 0

Þ A − B < 0 Þ A < B.

Câu 32: So sánh: $A=\frac{2017+2018}{2018+2019}$  và $B=\frac{2017}{2018}+\frac{2018}{2019}$ .

Lời giải:

Ta có: $A=\frac{2017+2018}{2018+2019}=\frac{2017}{2018+2019}+\frac{2018}{2018+2019}$ .

Ta thấy $\frac{2017}{2018+2019}<\frac{2017}{2018}\frac{2018}{2018+2019}<\frac{2018}{2019}$ ;

Nên $\frac{2017}{2018+2019}+\frac{2018}{2018+2019}<\frac{2017}{2018}+\frac{2018}{2019}$ .

Do đó A < B.

Câu 33: Tìm tất cả các giá tị thực của tham số m để hàm số

y = x³ − 3x² + (m + 1)x + 2 có hai điểm cực trị.

A. m £ 2;

B. m > 2;

C. m < 2;

D. m < −4.

Lời giải:

Ta có y = x³ − 3x² + (m + 1)x + 2

Þ y' = 3x² − 6x + m + 1

Hàm số y = x³ − 3x² + (m + 1)x + 2 có hai điểm cực trị

Û y' = 0 có hai nghiệm phân biệt

Û ∆' > 0 Û 3² − 3(m + 1) > 0 Û m < 2

Câu 34: Tìm tất cả các giá tị thực của tham số m để hàm số y = −x² + (m − 1)x + 2 nghịch biến trên khoảng (1; 2).

A. m < 5;

B. m > 5;

C. m < 3;

D. m > 3.

Lời giải:

Với mọi x₁ ≠ x₂, ta có:

$$\begin{gathered} \frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2} \\ =\frac{\left[-{x_1}^2+\left(m-1\right)x_1+2\right]-\left[-{x_2}^2+\left(m-1\right)x_2+2\right]}{x_1-x_2} \end{gathered}$$

= − (x₁ + x₂) + m − 1

Để hàm số nghịch biến trên (1; 2) Û − (x₁ + x₂) + m − 1 < 0, với mọi x₁, x₂ Î (1; 2)

Û m < (x₁ + x₂) + 1, với mọi x₁, x₂ Î (1; 2)

Û m < (1 + 1) + 1 = 3

Đáp án cần chọn là C.

Câu 35: Phân tích đa thức thành nhân tử: $x-2\sqrt{x}-3$ .

Lời giải:

Ta có $x-2\sqrt{x}-3=x-3\sqrt{x}+\sqrt{x}-3$

$=\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}-3=\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)$

Câu 36: Giải phương trình: $x-2\sqrt{x-3}=3$ .

Lời giải:

$x-2\sqrt{x-3}=3$ (ĐK: x ≥ 3)

$$\begin{gathered} \iff x-3-2\sqrt{x-3}=0 \\ \iff \sqrt{x-3}\left(\sqrt{x-3}-2\right)=0 \end{gathered}$$

+) TH1: $\sqrt{x-3}=0$

Û x − 3 = 0

Û x = 3 (TMĐK)

+) TH2: $\sqrt{x-3}=2$

Û x − 3 = 4

Û x = 7 (TMĐK)

Vậy x = 3 hoặc x = 7.

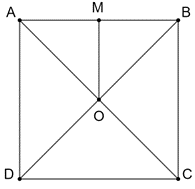
Câu 37: Cho hình vuông ABCD cạnh a, tâm O và M là trung điểm AB. Tính độ dài của các vectơ $\overrightarrow{OA}+\overrightarrow{OB}.$

Lời giải:

$\left|\overrightarrow{OA}+\overrightarrow{OB}\right|=2\left|\overrightarrow{OM}\right|=2OM=AD=a.$

Câu 38: Tính diện tích hình bình hành, biết tổng số độ dài đáy và chiều cao là 24 cm, độ dài đáy hơn chiều cao 4 cm.

Lời giải:

Độ dài đáy của hình bình hành đó là:

(24 + 4) : 2 = 14 (cm)

Chiều cao của hình bình hành đó là:

24 − 14 = 10 (cm)

Diện tích của hình bình hành đó là:

14 × 10 = 140 (cm²)

Đáp số: 140 cm²

Câu 39: Tính diện tích hình bình hành, biết tổng số độ dài đáy và chiều cao là 25 cm, độ dài cạnh đáy hơn chiều cao 7 cm.

Lời giải:

Độ dài đáy của hình bình hành đó là:

(25 + 7) : 2 = 16 (cm)

Chiều cao của hình bình hành đó là:

25 − 16 = 9 (cm)

Diện tích của hình bình hành đó là:

16 × 9 = 126 (cm²)

Đáp số: 126 cm²

Câu 40: Rút gọn phân thức sau: $\frac{x^2+4x+3}{2x+6}\left(x\ne -3\right)$ .

Lời giải:

Với điều kiện x ≠ −3, ta có:

$$\begin{gathered} \frac{x^2+4x+3}{2x+6} \\ =\frac{x^2+3x+x+3}{2\left(x+3\right)}=\frac{x\left(x+3\right)+x+3}{2\left(x+3\right)} \\ =\frac{\left(x+3\right)\left(x+1\right)}{2\left(x+3\right)}=\frac{x+1}{2} \end{gathered}$$

Câu 41: Thực hiện phép cộng: $\frac{6}{x^2+4x}+\frac{3}{2x+8}.$

Lời giải:

Ta có

$$\begin{gathered} \frac{6}{x^2+4x}+\frac{3}{2x+8}=\frac{6}{\left(x+4\right)x}+\frac{3}{2\left(x+4\right)} \\ =\frac{6.2}{2\left(x+4\right)x}+\frac{3x}{2x\left(x+4\right)} \\ =\frac{12}{2x\left(x+4\right)}+\frac{3x}{2x\left(x+4\right)} \\ =\frac{12+3x}{2x\left(x+4\right)}=\frac{3\left(x+4\right)}{2x\left(x+4\right)}=\frac{3}{2x} \end{gathered}$$

Câu 42: Giải phương trình $\cos \left(x+\frac{\pi }{3}\right)+\sin 2x=0$ .

Lời giải:

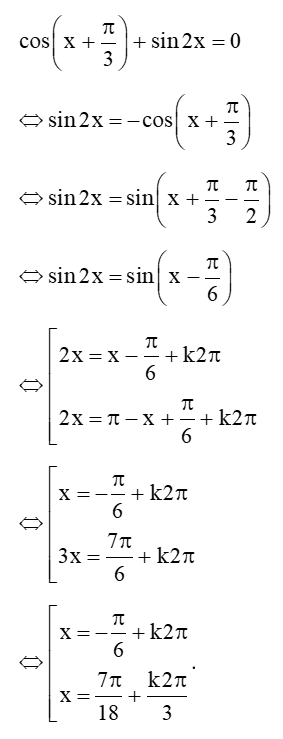
Câu 43: Giải phương trình $\sin 2x+\cos \left(6x+\frac{\pi }{3}\right)=0$ .

Lời giải:

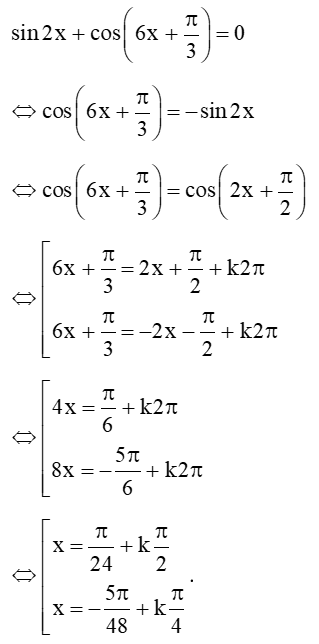
Câu 44: Rút gọn biểu thức: $A=\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}$ .

Lời giải:

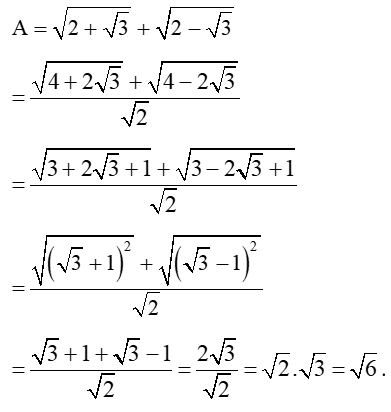
Câu 45: Rút gọn $\sqrt{2-\sqrt{3}}$ .

Lời giải:

Ta có

$$\begin{gathered} \sqrt{2-\sqrt{3}}=\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}} \\ =\frac{{\displaystyle \sqrt{3-2\sqrt{3}+1}}}{{\displaystyle \sqrt{2}}} \\ =\frac{{\displaystyle \sqrt{{\left(\sqrt{3}-1\right)}^2}}}{{\displaystyle \sqrt{2}}} \\ =\frac{{\displaystyle \sqrt{3}-1}}{{\displaystyle \sqrt{2}}}=\frac{{\displaystyle \sqrt{6}-\sqrt{2}}}{{\displaystyle 2}} \end{gathered}$$

Câu 46: Tìm giá trị lớn nhất của $\frac{3}{\sqrt{x}+3}$ .

Lời giải:

Do $\sqrt{x}\ge \mathrm{0,}\forall x\ge 0$

Nên $\sqrt{x}+3\ge 3\Rightarrow \frac{3}{\sqrt{x}+3}\le \frac{3}{3}=1$ .

Do đó giá trị lớn nhất của $\frac{3}{\sqrt{x}+3}$ $\frac{3}{\sqrt{x}+3}=1\iff \sqrt{x}=1\Rightarrow x=0$.

Vậy giá trị lớn nhất của $\frac{3}{\sqrt{x}+3}$  là 1 khi x = 0.

Câu 47: Tìm giá trị nhỏ nhất của $\frac{-3}{\sqrt{x}+3}$ .

Lời giải:

Do $\sqrt{x}\ge \mathrm{0,}\forall x\ge 0$

Nên $\sqrt{x}+3\ge 3\Rightarrow \frac{3}{\sqrt{x}+3}\le \frac{3}{3}=1$

$\Rightarrow \frac{-3}{\sqrt{x}+3}\ge -1$.

Vậy giá trị nhỏ nhất của $\frac{-3}{\sqrt{x}+3}$  là −1 khi và chỉ khi $\sqrt{x}=1\Rightarrow x=0$ .

Câu 48: Trong dịp tổng kết cuối năm lớp 6A không có học sinh yếu, kém. Biết 125 % số học sinh khá là 35 em. Số học sinh giỏi bằng $\frac{5}{7}$  số học sinh khá. Số học sinh  trung bình bằng 10 % số học sinh giỏi.

a) Tính số học sinh mỗi loại.

b) Số học sinh giỏi bằng bao nhiêu phần trăm số học sinh cả lớp?

Lời giải:

a) Số học sinh khá là:

35 : 125% = 28 (hoc sinh)

Số học sinh giỏi là:

28 . $\frac{5}{7}$  = 20 (học sinh)

Số học sinh trung bình là:

20 × 10% = 2 (học sinh).

b) Tỉ số phần trăm của số học sinh giỏi so với số học sinh cả lớp là:

$\frac{20}{28+20+2}\times 100\%=40\%$

Câu 49: Chứng minh $\sin 2a=2\sin a.\cos a$

Lời giải:

Ta có:

sin 2a = sin (a + a)

$=\sin a.\cos a+\cos a.\sin a=2\sin a.\mathrm{co}sa$

Câu 50: Cho tam giác ABC vuông tại A, AB < AC, góc C = a < 45°, đường trung tuyến AM, đường cao AH, MA = MB = MC. Chứng minh: $\sin 2\alpha =2\sin \alpha .\cos \alpha$

Lời giải:

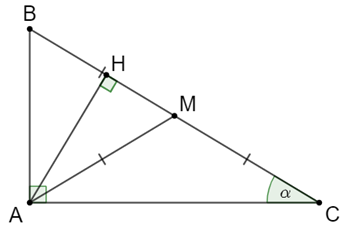
Ta có:

$$\begin{gathered} \sin 2\alpha =\sin \left(2\widehat{ACB}\right)=\sin \left(\widehat{MCA}+\widehat{MAC}\right) \\ =\sin \left(\widehat{AMH}\right)=\frac{AH}{AM}=\frac{2AH}{BC} \\ =2.\frac{AH}{AC}.\frac{AC}{BC}=2\sin \alpha .\cos \alpha \end{gathered}$$

Câu 51: Cho tam giác ABC vuông tại A, biết $\widehat{C}=52°$ . Hỏi số đo góc B bằng bao nhiêu?

Lời giải:

Áp dụng định lí tổng số đo ba góc trong một tam giác, ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}=180°-90°-52°=38°$ .

Vậy số đo góc B bằng 38^o.

Câu 52: Cho tam giác ABC. Chứng minh sin A = sin B.cos C + sin C.cos B.

Lời giải:

Ta có: sin B.cos C + sin C.cos B = sin (B + C)

$=\sin \left({180}^{\circ }-B-C\right)=\sin A$.

Do đó sin A = sin B.cos C + sin C.cos B (đpcm).

Câu 53: Chứng minh rằng trong tam giác ABC ta có các hệ thức:

a) sin A = sin B.cos C + sin C.cos B;

b) h_a = 2R.sin B.sin C.

Lời giải:

a) Ta có: sin B.cos C + sin C.cos B = sin (B + C)

$=\sin \left({180}^{\circ }-B-C\right)=\sin A$

b) Theo định lý sin ta có:  $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$.

Do đó: a = 2R.sin A, b = 2R.sin B, c = 2R.sin C.

Khi đó: 2R.sin B.sin C $=\frac{bc}{2R}=\frac{S_{ABC}}{R.\sin A}=\frac{2}{a}.\frac{1}{2}.h_a.a=h_a$ .

Câu 54: Cho tam giác ABC vuông tại A, đường cao AH (h.5). Giải bài toán trong mỗi trường hợp sau:

a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH. 

b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.

Lời giải:

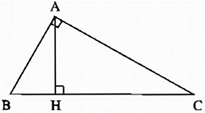
a) – Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: AH² = BH.CH

$\Rightarrow CH=\frac{A{H}^2}{BH}=\frac{{16}^2}{25}=\mathrm{10,24}$

BC = BH + CH = 25 + 10,24 = 35,24.

– Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

AB² = BH.BC

$\Rightarrow AB=\sqrt{BH.BC}=\sqrt{25.\mathrm{35,24}}=\mathrm{29,68}$

AC² = HC.BC

$\Rightarrow AC=\sqrt{CH.BC}=\sqrt{\mathrm{10,24}.\mathrm{35,24}}=\mathrm{18,99}$

b) – Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:   

AB² = BH.BC

$\Rightarrow BC=\frac{A{B}^2}{BH}=\frac{{12}^2}{6}=24$

CH = BC − BH = 24 − 6 = 18

– Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

AC² = HC.BC

$\Rightarrow AC=\sqrt{CH.BC}=\sqrt{18.24}=\mathrm{20,78}$

– Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:

AH² = BH.CH

$\Rightarrow AH=\sqrt{HB.HC}=\sqrt{6.18}=6\sqrt{3}$

Câu 55: Tìm tất cả các nghiệm nguyên của phương trình: 2x + 5y = 15.

Lời giải:

Ta có 2x + 5y = 15

$$\begin{gathered} \iff x=\frac{15-5y}{2} \\ \iff x=7-2y+\frac{1-y}{2} \end{gathered}$$

Vì x, y Î ℤ Þ 1 − y ⋮ 2

Þ 1 − y = 2m (m Î ℤ)

Û y = 1 − 2m (m Î ℤ)

$\iff x=\frac{15-5\left(1-2m\right)}{2}=5m+5$ (m Î ℤ)

Vậy các cặp nghiệm (x; y) nguyên thỏa mãn là (5m + 5; 1 − 2m), với m Î ℤ

Câu 56: Tìm tất cả các nghiệm nguyên của phương trình 5x − 3y = 8.

Lời giải:

Ta có 5x − 3y = 8

$$\begin{gathered} \iff y=\frac{5x-8}{3} \\ \iff y=x-2+\frac{2x-2}{3} \end{gathered}$$

Vì x, y Î ℤ Þ x − 1 ⋮ 3

Þ x − 1 = 3m

Û x = 3m + 1 (m Î ℤ)

$\iff y=\frac{5\left(3m+1\right)-8}{3}=5m-1$ (m Î ℤ)

Vậy các cặp nghiệm (x; y) nguyên thỏa mãn là (3m + 1; 5m − 1), với m Î ℤ.

Câu 57: Một hộp đựng 8 viên bi màu xanh, 5 viên bi đỏ, 3 viên bi màu vàng. Có bao nhiêu cách chọn từ hộp đó ra 4 viên bi trong đó có đúng 2 viên bi xanh?

Lời giải:

• TH1: Chọn 2 viên bi xanh, 2 viên bi đỏ có:

$C_8^2.C_5^2=280$ (cách).

• TH2: Chọn 2 viên bi xanh, 2 viên bi vàng có:

$C_8^2.C_3^2=84$ (cách).

• TH3: Chọn 2 viên bi xanh, 1 viên bi đỏ và 1 viên bi vàng có:

$C_8^2.C_5^1.C_3^1=420$ (cách).

Vậy có: 280 + 84 + 420 = 784 (cách).

Câu 58: Một hộp đựng 8 viên bi màu xanh, 5 viên bi đỏ, 3 viên bi màu vàng. Có bao nhiêu cách chọn từ hộp đó ra 4 viên bi sao cho số bi xanh bằng số bi đỏ?

Lời giải:

• TH1: Chọn 2 viên bi xanh, 2 viên bi đỏ có:

$C_8^2.C_5^2=280$ (cách).

• TH2: Chọn 1 viên bi xanh, 1 viên bi đỏ và 2 viên bi vàng có:

$C_8^1.C_5^1.C_3^2=120$ (cách).

Vậy có: 280 + 120 = 400 (cách).

Câu 59: Giải tam giác ABC vuông tại A, biết rằng: b = 8 cm, C = 60°

Lời giải:

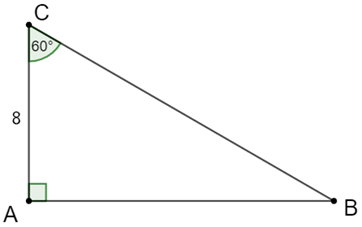
Ta có:

$$\begin{gathered} \widehat{B}=90°-\widehat{C}=90°-60°=30° \\ \cos C=\frac{AC}{BC}\Rightarrow BC=\frac{AC}{\cos C}=\frac{8}{\cos {60}^{\circ }}=16\left(cm\right) \\ AB=\sqrt{B{C}^2-A{C}^2}=\sqrt{{16}^2-8^2}=8\sqrt{3}\left(cm\right) \end{gathered}$$

Câu 60: Tìm x để x + 21 là bội của x + 3.

Lời giải:

Để x + 21 là bội của x + 3 nên

x + 21 ⋮ x + 3

(x + 3) + 18 ⋮ x + 3

18 ⋮ x + 3

Do đó x + 3 Î Ư(18) = {−18; −9; −6; −3; −2; −1; 1; 2; 3; 6; 9; 18}.

Vậy x Î {−21; −12; −9; −6; −5; −4; −2; −1; 0; 3; 6; 15}.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 9)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 10)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 11)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 12)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 13)