1500 câu hỏi ôn tập môn Toán có đáp án (Phần 3)

1500 câu hỏi ôn tập Toán (Phần 3)

Câu 1: Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4cm và HC = 6cm.

a) Tính độ dài các đoạn AH, AB, AC

b) Gọi M là trung điểm của AC. Tính số đó góc AMB (làm tròn đến độ)

c) Kẻ AK vuông góc BM (K thuộc BM). Chứng minh: $\frac{BK}{BH}=\frac{BC}{BM}$

Lời giải:

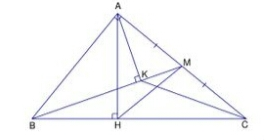
A_ Tính độ dài các đoạn AH, AB, AC

∆ABC vuông tại A:

+ $A{H}^2=HB.HC=4.6=24\Rightarrow AH=2\sqrt{6}\left(cm\right)$

+ $A{B}^2=BC.HB=10.4=40\Rightarrow AB=2\sqrt{10}\left(cm\right)$

+ $A{C}^2=BC.HC=10.6=60\Rightarrow AC=2\sqrt{15}\left(cm\right)$

b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn độ). ∆ABM vuông tại A

$tgAMB=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}\Rightarrow AMB\approx 59°$

c) Kẻ AK vuông góc với BM ( $K\in BM$ ). Chứng minh: $\Delta BKC~\Delta BHM$

∆ABM vuông tại A có: $AK\perp BM$

+ AB² = BK.BM

∆ABC vuông tại A có: $AH\perp BC$

+ AB² = BH.BC

$\Rightarrow BK.BM=BH.BC$ hay $\frac{BK}{BH}=\frac{BC}{BM}$

Câu 2: Cho điểm M có hoành độ là -2 và điểm M thuộc đồ thị hàm số y = −2x² . Xác định tọa độ điểm M

Lời giải:

Vì M ∈ y = −2x² và có hành độ là −2

Thay x = −2 vào hàm số y = −2x² ta có:

y = −2.(−2)²

⇔ y = −8

Vậy tọa độ điểm M là: M (−2; −8)

Câu 3: Cho hàm số y = x - 2 có đồ thị là d. Tìm điểm trên d có hoành độ và tung độ đối nhau

Lời giải:

Vì các điểm trên (d) có hoành độ và tung độ đối nhau nên

y = −x

Thay vào (d) ta được

− x = x – 2

⇔ x = 1

⇒ y = −1

Vậy điểm đó là (1; -1)

Câu 4: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C, vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:

a) Tứ giác ABCD nội tiếp.

b) CA là phân giác góc SCB.

Lời giải:

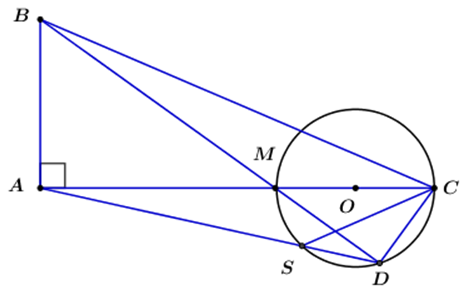
a) Tứ giác ABCD nội tiếp.

Do MC là đường kính của đường tròn (O), D thuộc (O) nên: ∠MDC = 90⁰ = ∠BAC

Suy ra D và A cùng nhìn BC dưới một góc vuông

⇒ Tứ giác ABCD nội tiếp đường tròn đường kính BC.

b) CA là phân giác góc SCB.

Do ABCD là tứ giác nội tiếp nên: $\widehat{ADB}=\widehat{ACB}$ (cùng chắn cung AB).

Xét (O) ta có: $\widehat{ACS}=\widehat{BDA}$ (hai góc nội tiếp cùng chắn cung MS)

⇒ ∠ACB = ∠ ACS ( = ∠BDA).

Vậy CA là phân giác của ∠SCB   (đpcm).

Câu 5: Cho đường tròn tâm O bán kỉnh và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB ?

Lời giải:

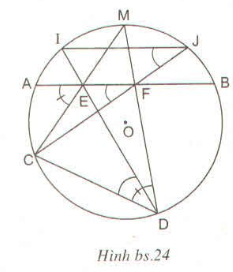
Xem hình vẽ (h.bs.24)

Ta có cung AM và MB bằng nhau nên $\widehat{AEC}=\widehat{CDM}$  (cùng bằng nửa số đo của cung nhỏ CM)

Suy ra CDFE là tứ giác nội tiếp.

Từ đó $\widehat{CDE}=\widehat{CFE}$  (cùng chắn cung CE)

Lại có $\widehat{IJC}=\widehat{IDC}$  (cùng chắn cung CI)

Vậy $\widehat{IJC}=\widehat{AFC}$ , suy ra JI song song với AB

Câu 6: Tìm chữ số tận cùng của các số: 
a) 7⁹⁹ 

b) 14¹⁴¹⁴  

c) 4⁵⁶⁷ 

Lời giải:

Trước hết, ta tìm số dư của phép chia 99 cho 4 : 
9⁹ - 1 = (9 - 1)(9⁸ + 9⁷ + … + 9 + 1) chia hết cho 4 
 99 = 4k + 1 (k thuộc N)

⇒ 7⁹⁹ = 7^{4k + 1} = 7^4k.7 
Do 7^4k có chữ số tận cùng là 1 (theo tính chất 1c)

⇒ 7⁹⁹ có chữ số tận cùng là 7.
b) Dễ thấy 14¹⁴ = 4k (k thuộc N)

⇒ theo tính chất 1d thì 14¹⁴¹⁴ = 14^4k có chữ số tận cùng là 6. 
c) Ta có 5⁶⁷ - 1 chia hết cho 4

⇒ 5⁶⁷ = 4k + 1 (k thuộc N) 
⇒ 4⁵⁶⁷ = 4^{4k + 1} = 4^4k.4, theo tính chất 1d, 4^4k có chữ số tận cùng là 6 nên 4⁵⁶⁷ có chữ số tận cùng là 4.

Câu 7: Cho hàm số y = 3x⁴ + 2(m − 2018)x² + 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng 120°

A. m = −2018

B. m = −2017

C. m = 2017

D. m = 2018.

Lời giải:

Ta có

y′ = 12x³ + 4(m − 2018)x;

$y\text{'}=0\iff \left[\begin{array}{c}x=0\\ 3x^2=2018-m\end{array}\right.$

Để hàm số có ba điểm cực trị ⇔ 2018 – m > 0 ⇔ m < 2018

Khi đó, tọa độ các điểm cực trị của đồ thị hàm số là:

A (0; 2017)

$$\begin{gathered} B\left(\sqrt{\frac{2018-m}{3}};-\frac{{\left(m-2018\right)}^2}{3}+2017\right) \\ C\left(-\sqrt{\frac{2018-m}{3}};-\frac{{\left(m-2018\right)}^2}{3}+2017\right) \end{gathered}$$

Do tam giác ABC cân tại A nên ycbt ⇔ 3AB² = BC²

$3\left[\frac{2018-m}{3}+\frac{{\left(m-2018\right)}^4}{9}\right]=4\frac{2018-m}{}3$

⇔ (m − 2018)³ = −1 ⇔ m = 2017 (thỏa mãn)

Câu 8: Cho hs: y = x⁴ + 2mx² + m² + m (1) ( m là tham số). Xác định m để hs (1) có 3 cực trị, đồng thời các điểm cực trị của đồ thị tạo thành 1 tam giác có góc bằng 120 độ.

Lời giải:

Ta có:
y′ = 4x³ + 4mx = 4x(x² + m)

Hàm số (1) có 3 cực trị khi và chỉ khi phương trình y′ = 0 có đúng 3 nghiệm phân biệt. Điều này tương đương với:
m < 0,   (2)
Với điều kiện (2), đồ thị hàm số có 3 điểm cực trị là :

$A\left(0;m^2+m\right),B\left(-\sqrt{-m};m\right),C\left(\sqrt{-m};m\right)$

Dễ thấy tam giác ABC là tam giác cân tại A. Do đó $\widehat{A}=120°$. Từ đó suy ra $\widehat{ABC}=30°$. Yêu cầu của bài toán tương đương với:

$\tan \widehat{ABC}=\frac{\left|y_A-y_B\right|}{\left|x_B\right|}\iff \frac{\sqrt{3}}{3}=\frac{m^2}{\sqrt{-m}}\iff m=-\frac{1}{3}$

$m=-\frac{1}{3}$ thỏa mãn (2) nên đó là đáp án của bài toán

Câu 9: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.

c) Chứng minh rằng: $S_{BHD}=\frac{1}{4}{S}_{BKC}.{\cos }^2\widehat{ABD}$ .

Lời giải:

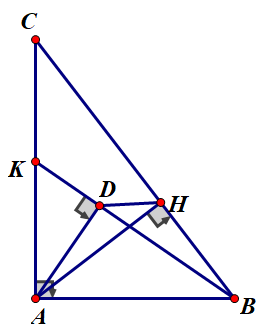
a) Áp dụng HTL tam giác:

$\left\{\begin{array}{c}A{B}^2=BH.BC=16\\ A{C}^2=BC.CH=8\left(8-2\right)=48\\ A{H}^2=BH.CH=2\left(8-2\right)=12\end{array}\right.\Rightarrow \left\{\begin{array}{c}AB=4\left(cm\right)\\ AC=4\sqrt{3}\left(cm\right)\\ AH=2\sqrt{3}\left(cm\right)\end{array}\right.$

b) $\widehat{ADB}=\widehat{AHB}\left(=90°\right)\Rightarrow$ ADHB nội tiếp

$\Rightarrow \widehat{DHA}=\widehat{DBA}$ (cùng chắn AD) (1)

$\left\{\begin{array}{c}\widehat{CKB}=\widehat{KAB}+\widehat{ABD}=90°+\widehat{ABD}\\ \widehat{DHB}=\widehat{DHA}+\widehat{AHB}=\widehat{DHA}+90°\\ \widehat{ABD}=\widehat{DHA}\left(cmt\right)\end{array}\right.$

$$\begin{gathered} \Rightarrow \widehat{CKB}=\widehat{DHB} \\ \left\{\begin{array}{c}\widehat{CKB}=\widehat{DHB}\\ \widehat{CBK}chung\end{array}\right.\Rightarrow \Delta DHB~\Delta CKB\left(g.g\right) \\ \Rightarrow \frac{BD}{BC}=\frac{BH}{BK}\Rightarrow BD.BK=BH.BC \end{gathered}$$

c) Áp dụng công thức tính diện tích hình tam giác bằng nửa tích hai cạnh nhân sin góc xen giữa

$S_{BHD}=\frac{1}{2}BH.BD.\sin \widehat{DBH}$

$S_{BKC}=\frac{1}{2}BK.BC.\sin \widehat{KBC}$

Mà $\widehat{DBH}=\widehat{KBC}$

$\Rightarrow \frac{S_{BHD}}{S_{BKC}}=\frac{BH.BD}{BK.BC}=\frac{2BD}{8BK}=\frac{BD}{4BK}=\frac{B{D}^2}{4BK.BD}$

$=\frac{1}{4}\frac{B{D}^2}{A{B}^2}$ (hệ thức lượng) $=\frac{1}{4}.{\cos }^2\widehat{ABD}$

$\Rightarrow S_{BHD}=\frac{1}{4}{S}_{BKC}.{\cos }^2\widehat{ABD}$.

Câu 10: Cho tam giác ABC có diện tích 60cm². Gọi M, N lần lượt là trung điểm của BC và AC. Tính diện tích tam giác AMN ?

Lời giải:

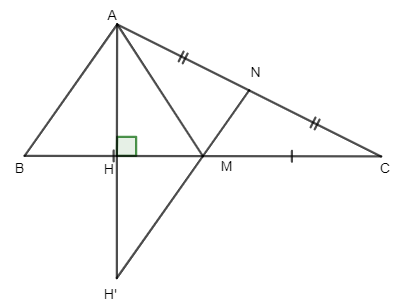
Vẽ $AH\perp BC$  cắt MN tại H'

Ta có :  $AH\text{'}=HH\text{'}=\frac{1}{2}AH$ (vì MN là trung điểm $\Rightarrow \frac{\text{1}}{\text{2}}\text{AH}$ )

Lại có:

${\text{S}}_{\text{ABC}}\text{= }\frac{\text{1}}{\text{2}}{\text{ . AH . BC = 60cm}}^{\text{2}}$ và ${\text{S}}_{\text{AMN}}\text{=}\frac{\text{1}}{\text{2}}\text{.MN}$ . Mà

${\text{S}}_{\text{AMN}}\text{= }\frac{\text{1}}{\text{2}}\text{ . }\frac{\text{1}}{\text{2}}\text{AH . }\frac{\text{1}}{\text{2}}\text{BC = }\frac{\text{1}}{\text{4}}\left(\frac{\text{1}}{\text{2}}\text{AH . BC}\right)\text{ = }\frac{\text{1}}{\text{2}}\text{ . 60 = 15}\left({\text{cm}}^{\text{2}}\right)$

Vậy ${\text{S}}_{\text{AMN}}{\text{ = 15cm}}^{\text{2}}$ .

Câu 11: Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S.

Lời giải:

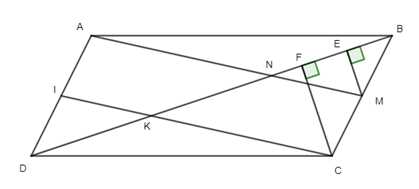
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ $ME \perp BD$  tại E, $CF \perp BD$ tại F.

Ta có 

$$\begin{gathered} \text{BN = }\frac{\text{1}}{\text{3}}\text{BD, EM = }\frac{\text{1}}{\text{2}}\text{CF} \\ {\text{S}}_{\text{BMN}}\text{ = }\frac{\text{1}}{\text{2}}\text{EM.BN = }\frac{\text{1}}{\text{2}}\text{ . }\frac{\text{1}}{\text{2}}\text{CF . }\frac{\text{1}}{\text{3}}\text{BD = }\frac{\text{1}}{\text{6}}{\text{S}}_{\text{BCD}}\text{=}\frac{\text{1}}{\text{12}}\text{S} \\ \Rightarrow {\text{S}}_{\text{MNDC}}\text{= }\frac{\text{1}}{\text{2}}\text{S - }\frac{\text{1}}{\text{12}}\text{S = }\frac{\text{5}}{\text{12}}\text{S} \end{gathered}$$

Câu 12: Có bao nhiêu số nguyên âm m để hàm số $\text{y = }\frac{\text{1}}{\text{3}}{\text{cos}}^{\text{3}}\text{x - 4cotx - }\left(\text{m + 1}\right)\text{ cosx}$ đồng biến trên khoảng $\left(0;\pi \right)$ ?

A. 5

B. 2

C. Vô số

D. 3

Lời giải:

Ta có:

$y\text{'}=-{\cos }^{2}x.\mathrm{s}\text{inx}+\frac{4}{\mathrm{s}{\text{in}}^2\text{x}}+\left(m+1\right).\mathrm{s}\text{inx}=\mathrm{s}{\text{in}}^3\text{x + }\frac{4}{\mathrm{s}{\text{in}}^2\text{x}}+m.\mathrm{s}\text{inx}$

- Hàm số đồng biến trến $\left(0;\pi \right)$  khi và chỉ khi $y\text{'}\ge \mathrm{0,}\forall x\in \left(0;\pi \right)$

$$\begin{gathered} \iff \mathrm{s}{\text{in}}^3\text{x + }\frac{4}{\mathrm{s}{\text{in}}^2\text{x}}+m.\mathrm{s}\text{inx}\ge \mathrm{0,}\forall x\in \left(0;\pi \right) \\ \iff \mathrm{s}{\text{in}}^2\text{x+}\frac{4}{\mathrm{s}{\text{in}}^3\text{x}}\ge -m,\forall x\in \left(0;\pi \right)\left(1\right) \end{gathered}$$

- Xét hàm số: $g\left(x\right)=\mathrm{s}{\text{in}}^2\text{x +}\frac{4}{\mathrm{s}{\text{in}}^3\text{x}}$ trên $\left(0;\pi \right)$

Có $g\text{'}\left(x\right)=2\sin x.\cos x-\frac{12\cos x}{{\sin }^{4}x}$

$$\begin{gathered} =2\cos x.\left(\sin x-\frac{6}{{\sin }^{4}x}\right)=2\cos x.\frac{{\sin }^{5}x-6}{{\sin }^{4}x} \\ \Rightarrow g\text{'}\left(x\right)=0\iff x=\frac{\pi }{2}\in \left(0;\pi \right) \end{gathered}$$

Bảng biến thiên

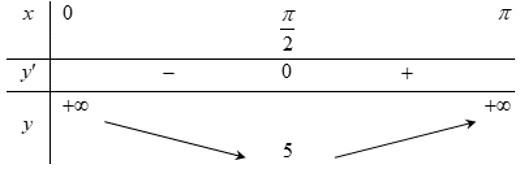
- Do đó : $\left(1\right)\iff -m\le \underset{x\in \left(0;\pi \right)}{\min }g\left(x\right)\iff -m\le 5$

$\iff m\ge -5$

- Lại do m nguyên âm nên $m\in \left\{-5;-4;-3;-2;-1\right\}$

Vậy có 5 số nguyên âm.

Câu 13: Tìm x ∈ BC(16; 21; 25) và x ≤ 400

Lời giải:

Ta có: 16 = 2⁴; 21 = 3.7; 25 = 5²

Suy ra BCNN(16; 21; 25) = 2⁴.3.5².7 = 8 400.

Do đó BC(16; 21; 25) = B(8 400) = {0; 8400; ...}.

Mà x ≤ 400 nên x = 0.

Vậy x = 0.

Câu 14: Cho tam giác ABC vuông ở B, trên cạnh AC lấy điểm E sao cho AE = AB. Tia phân giác của góc A cắt BC tại D.

a, Chứng minh $\Delta ADB=\Delta ADE$

b, Chứng minh $DE\perp AC$

c, Một đường thẳng qua C và vuông góc với AD cắt đường thẳng AB ở F. Chứng minh BF = CE

Lời giải:

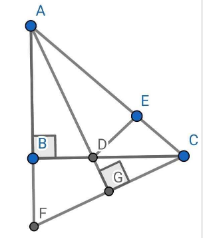
a) Xét $\Delta ADB$ và $\Delta ADE$ có:

AD chung

$\widehat{BAD}=\widehat{EAD}$ (AD là tia phân giác của $\widehat{BAC}$ )

AB = AE (gt)

$\Rightarrow \Delta ADB=\Delta ADE\left(c-g-c\right)$

b) Do $\Delta ADB=\Delta ADE\left(c-g-c\right)$

$\Rightarrow \widehat{ABD}=\widehat{AED}$ (hai góc tương ứng)

$\Rightarrow \widehat{AED}={90}^0$

Hay DE vuông góc AC

c) Gọi G là giao điểm của CF và AD

Do $\widehat{BAD}=\widehat{EAD}$  (cmt)

$\Rightarrow \widehat{FAG}=\widehat{CAG}$

Xét hai tam giác vuông: $\Delta AGF$ và $\Delta AGC$ có:

AG chung

$\widehat{FAG}=\widehat{CAG}$ (cmt)

$\Rightarrow \Delta AGF=\Delta AGC$ (cạnh góc vuông - góc nhọn kề)

$\Rightarrow AF=AC$ (hai cạnh tương ứng)

Mà $AF=AB+BF$

$$\begin{gathered} AC=AE+EC \\ AB=AE \\ \Rightarrow BF=CE \end{gathered}$$

Câu 15: Cho đường tròn tâm O, đường kính AB và một điểm C di động trên đoạn AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F

a. Chứng minh tứ giác MECF là hình chữ nhật và EF là tiếp tuyến chung của (I) và (K)

b. Cho AB = 4cm, xác định vị trí điểm C trên AB để diện tích tứ giác IFEK là lớn nhất.

c. Khi C khác O, đường tròn ngoại tiếp hình chữ nhật MECF cắt đường trong (O) tại P (khác M), đường thẳng PM cắt đường thẳng AB tại N. Chứng minh tam giác MPF đồng dạng với tam giác MBN.

d. Chứng minh 3 điểm: N, E, F thẳng hàng

Lời giải:

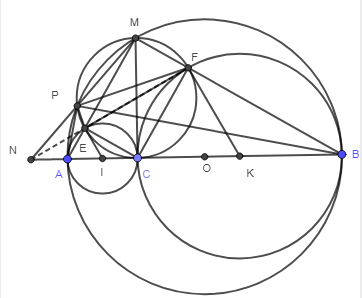
a) Ta thấy MEC và MFC là các tam giác vuông chung cạnh huyền MC nên MECF nội tiếp đường tròn đường kính MC.

Dễ thấy MECF là hình chữ nhật (Tứ giác có 3 góc vuông) nên $\widehat{\text{CEF}}\text{=}\widehat{\text{ECM}}$

Lại có $\widehat{\text{IEC}}\text{=}\widehat{\text{ICE}}\Rightarrow \widehat{\text{IEF}}\text{=}\widehat{\text{MCA}}{\text{=90}}^{\text{o}}$

Hoàn toàn tương tự FE là tiếp tuyến đường tròn (K). Vậy EF là tiếp tuyến chung của hai đường tròn.

b) MECF là hình chữ nhật nên EF = MC.

Do EI và FK cùng vuông góc với EF nên IEFK là hình thang vuông.

$\Rightarrow {\text{S}}_{\text{IEFK}}\text{=}\frac{\left(\text{EI+FK}\right)\text{.EF}}{\text{2}}\text{=}\frac{\left(\text{IC+CK}\right)\text{.MC}}{\text{2}}\text{=}\frac{\text{IK.MC}}{\text{2}}\text{=}\frac{\frac{\text{AB}}{\text{2}}\text{.MC}}{\text{2}}\text{=MC}\le \text{MH}$ với H là điểm chính giữa cung AB.

Vậy để diện tích IEFK lớn nhất thì C nằm chính giữa cung AB. Khi đó 

${\text{S}}_{\text{IEFK}}\text{=2}\left({\text{cm}}^{\text{2}}\right)$

c) Ta thấy $\widehat{\text{MPF}}\text{=}\widehat{\text{MCF}}$  (Hai góc nội tiếp cùng chắn cung MF) $=\widehat{\text{MBN}}$  (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung CF)

$\Rightarrow \text{ΔMPF ~ ΔMBN}\left(\text{g - g}\right)$

d) Do $\text{ΔMPF ~ ΔMBN}\Rightarrow \widehat{\text{MFP}}\text{ =}\widehat{\text{ MNB}}$

Mà $\widehat{\text{MFP }}\text{=}\widehat{\text{ MEP}}\Rightarrow \widehat{\text{PNA}}\text{ =}\widehat{\text{ MEP}}$  hay NPEA là tứ giác nội tiếp.

Tương tự PFBN cũng là tứ giác nội tiếp.

Vậy thì ta có: $\widehat{\text{PNE}}\text{ = }\widehat{\text{PAE}}\text{ =}\widehat{\text{ PBM}}\text{ =}\widehat{\text{ PNF}}$

Hay N, E, F thẳng hàng.

Câu 16: Cho đường tròn (O) đường kính AB, vẽ góc ở tâm  $\widehat{AOC}={55}^0$. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE.

A. 55⁰

B. 60⁰

C. 40⁰

D. 50⁰

Lời giải:

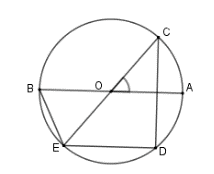
Xét (O) có $CD\perp OA;ED//OA$

$\Rightarrow CD\perp ED$ hay $\widehat{EDC}={90}^0$

Mà E; D; C $\in \left(O\right)$ nên EC là đường kính của (O) hay E; O; C thẳng hàng.

Do đó $\widehat{BOE}=\widehat{COA}={55}^0$ (đối đỉnh) nên số đo cung nhỏ BE là 55°.

Đáp án cần chọn là: A.

Câu 17:  Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh: ME = AD và MD = AE.

Lời giải:

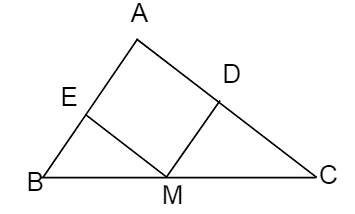
Xét tứ giác AEMD có : MD // AE (vì MD // AB) và ME // AD (vì ME // AC)

⇒ AEMD là hình bình hành. Theo tính chất của hình bình hánh ta suy ra được ME = AD và MD = AE (đpcm).

Câu 18: Cho tam giác ABC vuông tại A. Từ điểm M bất kì trên cạnh BC ( M không trùng với BC ) kẻ đường thẳng song song với AC và AB, chúng cắt AB ở D và AC ở E.

a) ADME là hình gì? Vì sao?

b) Giả sử AD và 3cm, AE = 4cm. Tính độ dài đoạn thẳng AM và diện tích tam giác DME

Lời giải:

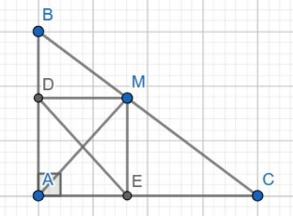
a)

Ta có: $\text{MD//AC, AB}\perp \text{AC}\left(gt\right)$

$\Rightarrow \text{MD}\perp \text{AB}$

Tương tự $\Rightarrow ME\perp AC$

Xét tứ giác ADME:

$\begin{array}{l}\widehat{\text{DAE}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(AB}\perp \text{AC)}\\ \text{}\widehat{\text{ADM}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}(MD}\perp \text{AB)}\\ \text{}\widehat{\text{AEM}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}(ME}\perp \text{AC)}\end{array}$

→ Tứ giác ADME là hình chữ nhật (tứ giác có 3 góc vuông)

→ AD = ME, DM = AE

b)

Ta có: AD = ME = 3cm, DM = AE = 4cm

$\Delta \text{ADM}$ vuông tại D:

${\text{AD}}^{\text{2}}{\text{ + DM}}^{\text{2}}{\text{ = AM}}^{\text{2}}$ (định lý Pytago)

$\Rightarrow \text{AM = }\sqrt{{\text{AD}}^{\text{2}}{\text{+DM}}^{\text{2}}}\text{ = }\sqrt{{\text{3}}^{\text{2}}{\text{+4}}^{\text{2}}}\text{ = 5(cm)}$

$\Delta DME$ vuông tại M

$\Rightarrow {\text{S}}_{\text{VDME}}\text{ = }\frac{\text{1}}{\text{2}}\text{.DM.ME = }\frac{\text{1}}{\text{2}}{\text{.4.3 = 6(cm}}^{\text{2}}\text{)}$

Câu 19: Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.

Nếu $A \cap B= \varnothing$ thì $A\backslash B=\mathrm{...}$ và $B\backslash A=\mathrm{....}$

Lời giải:

Ta có $A \cap B= \varnothing$ nên A và B là hai tập hợp rời nhau:

Khi đó mọi phần tử của A và B đều khác nhau.

Vậy $A\backslash B=A$ và $B\backslash A=B$ .

Câu 20: Hai xạ thủ độc lập với nhau cùng bắn vào một tấm bia. Mỗi người bắn một viên. Xác suất bắn trúng của xạ thủ thứ nhất là 0,7; của xạ thủ thứ hai là 0,8. Gọi X là số viên đạn bắn trúng bia. Tính kì vọng của X :

A. 1,75

B. 1,5

C. 1,54

D. 1,6

Lời giải:

Xác suất để 2 người không bắn trúng bia là: P = 0,3 . 0,2 = 0, 06.

Xác suất để 2 người cùng bắn trúng bia là:  P = 0,7 . 0,8 = 0,56.

Xác suất để đúng 1 người cùng bắn trúng bia là: P = 1 – 0,06 – 0,56 = 0,38.

Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc X .

X	0	1	2
P	0,06	0,38	0,56

Vậy kỳ vọng của X là E(X) = 0 . 0,06 + 1 . 0,38 + 2 . 0,56 = 1,5.

Câu 21: Hai xạ thủ A và B cùng bắn vào bia xác suất để xạ thủ bắn trúng là 0,7 và xác suất để xạ thủ b bán kính là 0,8 tính xác suất để có đúng một xạ thủ bắn trúng bia

Lời giải:

Có đúng 1 người bắn trúng bia → (A trúng, B trật) hoặc (A trật, B trúng)

→ xác suất  $P=\mathrm{0,7.}\left(1-\mathrm{0,8}\right)+\left(1-\mathrm{0,7}\right)\mathrm{.0,8}=\mathrm{0,38}$.

Câu 22: Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
A. 20;

B. 45;

C. 38;

D. 21.

Lời giải:

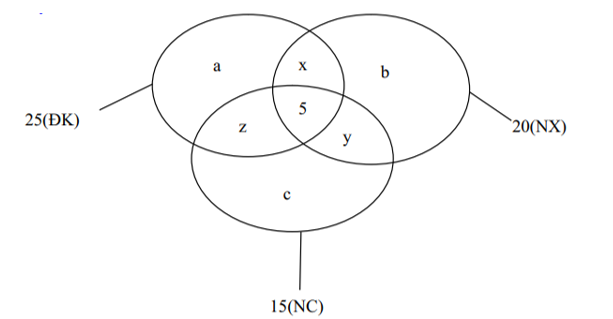
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: 45 –  7 = 38
Dựa vào biểu đồ ven ta có hệ phương trình sau:

$\left\{\begin{array}{c}a+x+z+5=25\left(1\right)\\ b+x+y+5=20\left(2\right)\\ c+y+z+5=15\left(3\right)\\ x+y+z+a+b+c+5=38\left(4\right)\end{array}\right.$

Cộng vế với vế của (1), (2), (3) ta có: a + b + c + 2(x + y + z) + 15 = 60 (5)

Từ (4) và (5) ta có: a + b + c + 2(38 – 5 – a – b – c) + 15 = 60

⟺ a + b + c = 21.

Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.

Câu 23: Trong hội khỏe Phù Đổng của trường THPT Thanh Miện, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 học sinhkhông tham gia môn nào, 5 học sinhtham gia cả 3 môn. Hỏi số học sinh tham gia chỉ một môn trong ba môn trên là bao nhiêu?

Lời giải:

Tổng số lượt đi thi là 25 + 20 + 15 = 60 (lượt)

Trong đó có 55 học sinh thi cả 33 môn

→ Có 60 – 5 . 3 = 45 lượt đi thi cho 40 – 7 = 33 học sinh

hay 45 lượt thi sẽ có xx học sinh và yy học sinh thi 2 trong 3 môn

$\left\{\begin{array}{c}x+y=33\\ x+2y=45\end{array}\right.\iff \left\{\begin{array}{c}x=21\\ y=12\end{array}\right.$

Vậy có 21 học sinh chỉ thi 1 trong 3 môn.

Câu 24: Cho a,b,c là các số không âm thỏa mãn a + b + c = 1. Chứng minh $b+c\ge 16abc$

Lời giải:

Ta có:

$a+b+c=1\Rightarrow a=1-b-c$

Điều phải cm

$$\begin{gathered} \iff b+c\ge 16\left(1-b-c\right)bc \\ \iff b+c-16\left(1-b-c\right)bc\ge 0 \\ \iff b+c-16bc+16b^{2}c+16b{c}^2\ge 0 \\ \iff \left(16b^{2}c-8bc+c\right)+\left(16b{c}^2-8bc+b\right)\ge 0 \\ \iff c\left(16b^2-8bc+1\right)+b\left(16c^2-8c+1\right)\ge 0 \end{gathered}$$

$\iff c{\left(4b-1\right)}^2+b{\left(4c-1\right)}^2\ge 0$ (luôn đúng)

→đpcm

Dấu “=” xảy ra $\left(a,b,c\right)\in \left\{\left(\mathrm{1,0,0}\right);\left(\frac{1}{2},\frac{1}{4},\frac{1}{4}\right)\right\}$

Câu 25: Cho tam giác ABC nhọn có đường cao AH. Gọi M và N là hình chiếu của H lên AB và AC. CMR: AB . AM = AC . AN

Lời giải:

Xét tứ giác AMHN có $\widehat{ANM}=\widehat{AHM}$ (1) (2 góc trong tứ giác nội tiếp cùng nhìn xuống cạnh AM)

Mà $\widehat{AHM}=\widehat{B}={90}^o –\widehat{BHM}\left(2\right)$

(1)(2) ⇒ $\widehat{ANM}=\widehat{B}$

Xét tam giác ANM và tam giác ABC có:

$\widehat{A}$ chung

$\widehat{ANM}=\widehat{B}$

tam giác ANM đồng dạng tam giác ABC (g – g)

$\frac{AN}{AB}=\frac{AM}{AC}\Rightarrow AN.AC=AB.AM$

Câu 26: Tìm hệ số của x⁶ trong khai triển ${(\frac{1}{x}+x^3)}^{3n+1}$ với $x\ne \mathrm{0,}$ biết n là số nguyên dương thỏa mãn điều kiện ${\text{3C}}_{\text{n\hspace{0.05em}+1}}^{\text{2}}{\text{+nP}}_{\text{2}}{\text{=4A}}_{\text{n}}^{\text{2}}$

 A.210.                   

B.252.                       

C.120.                    

D.45.

Lời giải:

Điều kiện:$\text{n}\ge \text{2.}$ Ta có

$\begin{array}{l}{\text{3C}}_{\text{n\hspace{0.05em}+1}}^{\text{2}}{\text{+ nP}}_{\text{2}}{\text{= 4A}}_{\text{n}}^{\text{2}}\\ \iff \text{3.}\frac{\left(\text{n+1}\right)\text{!}}{\left(\text{n-1}\right)\text{!.2!}}\text{ + 2n = 4.}\frac{\text{n!}}{\left(\text{n-2}\right)\text{!}}\\ \iff \frac{\text{3}}{\text{2}}\text{n}\left(\text{n + 1}\right)\text{ + 2n = 4n}\left(\text{n-1}\right)\end{array}$

$\begin{array}{l}\iff \text{3}\left(\text{n + 1}\right)\text{ + 4 = 8}\left(\text{n-1}\right)\\ \iff \text{3n + 3 + 4 = 8n - 8}\\ \iff \text{5n = 15}\\ \iff \text{n = 3.}\end{array}$

Với n = 3, theo khai triển nhị thức Newton, ta có

${\left(\frac{\text{1}}{\text{x}}{\text{+x}}^{\text{3}}\right)}^{\text{10}}\text{=}\sum _{k=0}^{10}{\text{C}}_{\text{10}}^{\text{k}}\text{.}{\left(\frac{\text{1}}{\text{x}}\right)}^{\text{10\hspace{0.05em}-\hspace{0.05em}k}}\text{.}{\left({\text{x}}^{\text{3}}\right)}^{\text{k}}\text{=}\sum _{k=0}^{10}{\text{C}}_{\text{10}}^{\text{k}}\text{.}\frac{{\text{x}}^{\text{3k}}}{{\text{x}}^{\text{10\hspace{0.05em}-\hspace{0.05em}k}}}\text{=}\sum _{k=0}^{10}{\text{C}}_{\text{10}}^{\text{k}}{\text{.x}}^{\text{4k\hspace{0.05em}-\hspace{0.05em}10}}\text{.}$

Hệ số của số hạng chứa x⁶ ứng với 4k – 10 = 6 k = 4

→ Hệ số cần tìm là $C_{10}^4=210.$

Đáp án cần chọn là: A

Câu 27: Cho n là số nguyên dương thỏa mãn điều kiện ${\text{6C}}_{\text{n+1}}^{\text{n-1}}{\text{ = A}}_{\text{n}}^{\text{2}}\text{ + 160.}$  Tìm hệ số của x⁷ trong khai triển $\left({\text{1 - 2x}}^{\text{3}}\right){\left(\text{2 + x}\right)}^{\text{n}}$

A. -2224

B. 2224

C. 1996

D. -1996

Lời giải:

Đáp án cần chọn là: A

Điều kiện: $\text{n}\ge \text{2}$

Từ giả thiết, ta có:

$\begin{array}{l}{\text{6C}}_{\text{n+1}}^{\text{n-1}}{\text{ = A}}_{\text{n}}^{\text{2}}\text{ + 160}\\ \iff \text{6.}\frac{\left(\text{n+1}\right)\text{!}}{\left(\text{n-1}\right)\text{!.2!}}\text{ = }\frac{\text{n!}}{\left(\text{n-2}\right)\text{!}}\text{ + 160}\\ \iff \text{3n}\left(\text{n + 1}\right)\text{ = n}\left(\text{n - 1}\right)\text{ + 160}\\ \iff {\text{2n}}^{\text{2}}\text{ + 4n - 160 = 0}\end{array}$

$\iff \text{n = 8}$ (vì điều kiện $n\ge 2$ )

Khi đó, ta được khai triển $\left({\text{1 - 2x}}^{\text{3}}\right){\left(\text{2 + x}\right)}^{\text{8}}\text{= }{\left(\text{2 + x}\right)}^{\text{8}}{\text{ - 2x}}^{\text{3}}{\left(\text{2 + x}\right)}^{\text{8}}$

Theo khai triển nhị thức Newton, ta có:

${\left(\text{2 + x}\right)}^{\text{8}}\text{=}\sum _{k=0}^8{\text{C}}_{\text{8}}^{\text{k}}{\text{.2}}^{\text{8-k}}{\text{.x}}^{\text{k}}$

Suy ra hệ số của x⁷ ứng với $k+3=7\iff k=4$

Hệ số của x⁷ trong khai triển ${\text{x}}^{\text{3}}{\left(\text{2+x}\right)}^{\text{8}}$ là ${\text{2}}^{\text{4}}{\text{.C}}_{\text{8}}^{\text{4}}$

Vậy hệ số cần tìm là ${\text{2.C}}_{\text{8}}^{\text{7}}{\text{ - 2.2}}^{\text{4}}{\text{.C}}_{\text{8}}^{\text{4}}\text{ = -2224}$ .

Câu 28: Chứng minh: $S=1+\frac{1}{2}+\frac{1}{3}+\cdot \cdot \cdot +\frac{1}{63}+\frac{1}{64}>4$ .

Lời giải:

Ta có:

$$\begin{gathered} S=1+\frac{1}{2}+\frac{1}{3}+\cdot \cdot \cdot +\frac{1}{63}+\frac{1}{64} \\ =1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+\cdot \cdot \cdot +\left(\frac{1}{33}+\frac{1}{34}+\cdot \cdot \cdot +\frac{1}{64}\right) \\ >1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)+\cdot \cdot \cdot +\left(\frac{1}{64}+\cdot \cdot \cdot +\frac{1}{64}\right) \\ =1+\frac{1}{2}+2\cdot \frac{1}{4}+4\cdot \frac{1}{8}+8\cdot \frac{1}{16}+16\cdot \frac{1}{32}+32\cdot \frac{1}{64} \\ =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=4 \end{gathered}$$

Vậy $S=1+\frac{1}{2}+\frac{1}{3}+\cdot \cdot \cdot +\frac{1}{63}+\frac{1}{64}>4$ .

Câu 29: Tìm m để hàm số $y=\frac{\sqrt{x-2m+3}}{x-m}+\frac{3x-1}{\sqrt{-x+m+5}}$  xác định trên khoảng (0; 1)?

Lời giải:

Điều kiện: $\left\{\begin{array}{l}x-2m+3\ge 0\\ x-m\ne 0\\ -x+m+5\ge 0\end{array}\right.\iff \left\{\begin{array}{l}x\ge 2m-3\\ x\ne m\\ x\le m+5\end{array}\right.$

Þ TXĐ: $D=\left[2m-3;m+5\right]\backslash \left\{m\right\}$

Để hàm số xác định trên khoảng (0; 1) thì (0; 1) là con của $D=\left[2m-3;m+5\right]\backslash \left\{m\right\}$

$$\begin{gathered} \iff \left\{\begin{array}{l}2m-3\le 0\\ m+5\ge 1\\ \left[\begin{array}{l}m\le 0\\ m\ge 1\end{array}\right.\end{array}\right.\iff \left\{\begin{array}{l}m\le \frac{3}{2}\\ m\ge -4\\ \left[\begin{array}{l}m\le 0\\ m\ge 1\end{array}\right.\end{array}\right. \\ \iff \left[\begin{array}{l}\left\{\begin{array}{l}m\le \frac{{\displaystyle 3}}{{\displaystyle 2}}\\ m\ge -4\\ m\le 0\end{array}\right.\\ \left\{\begin{array}{l}m\le \frac{{\displaystyle 3}}{{\displaystyle 2}}\\ m\ge -4\\ m\ge 1\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}-4\le m\le 0\\ 1\le m\le \frac{{\displaystyle 3}}{{\displaystyle 2}}\end{array}\right. \end{gathered}$$

Vậy $m\in \left[-4;0\right]\cup \left[1;\frac{3}{2}\right].$

Câu 30: Tìm tất cả các giá trị thực của tham số m để hàm số

$y=\sqrt{x-m+1}+\frac{2x}{\sqrt{-x+2m}}$ xác định trên khoảng (−1; 3).

A. Không có giá trị m thỏa mãn;

B. m ≥ 2;

C. m ≥ 3;

D. m ≥ 1.

Lời giải:

Điều kiện: $\left\{\begin{array}{l}x-m+1\ge 0\\ -x+2m>0\end{array}\right.\iff \left\{\begin{array}{l}x\ge m-1\\ x<2m\end{array}\right.$

Þ TXĐ: $D=\left[m-1;2m\right]$

Để hàm số xác định trên khoảng (−1; 3) thì (−1; 3) là con của $D=\left[m-1;2m\right]$

$\iff \left\{\begin{array}{l}m-1\le -1\\ 2m\ge 3\end{array}\right.\iff \left\{\begin{array}{l}m\le 0\\ m\ge \frac{3}{2}\end{array}\right.$

Vậy không có giá trị của m nào thỏa mãn.

Vậy ta chọn đáp án A.

Câu 31: Tìm x biết x³ − 3x + 2 = 0.

Lời giải:

x³ − 3x + 2 = 0

Û x³ − x − 2x + 2 = 0

Û x(x² − 1) − 2(x − 1) = 0

Û x(x − 1)(x + 1) − 2(x − 1) = 0

Û (x − 1)(x² + x − 2) = 0

Û (x − 1)[x² − x + 2x − 2] = 0

Û (x − 1)[x(x − 1) + 2(x − 1)] = 0

Û (x − 1)²(x + 2) = 0

$\Rightarrow \left[\begin{array}{l}x-1=0\\ x+2=0\end{array}\right.\iff \left[\begin{array}{c}x=1\\ x=-2\end{array}\right.$

Vậy nghiệm của phương trình là x = 1 và x = −2.

Câu 32: Cho hai tập hợp $E=\left(2;5\right]$  và $F=\left[2m-3;2m+2\right]$ . Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.

Lời giải:

Do (2m + 2) − (2m − 3) = 5 nên độ dài của tập F bằng 5.

Để $C=E\cup F$  là một đoạn có độ dài bằng 5 khi và chỉ khi C = F.

$\iff E\subset F$

$\iff \left\{\begin{array}{l}2m-3\le 2\\ 2m+2\ge 5\end{array}\right.\iff \left\{\begin{array}{l}m\le \frac{5}{2}\\ m\ge \frac{3}{2}\end{array}\right.\iff \frac{3}{2}\le m\le \frac{5}{2}$.

Vậy các giá trị của tham số m thỏa mãn yêu cầu bài toán là $m\in \left[\frac{3}{2};\frac{5}{2}\right]$ .

Câu 33: Tìm m để đa thức: A(x) = x³ − 3x² + 5x + m chia hết cho đa thức B(x) = x − 2

Lời giải:

Ta có A(x) = x³ − 3x² + 5x + m

= (x³ − 2x²) − (x² − 2x) + (3x − 6) + m + 6

= x²(x − 2) − x(x − 2) + 3(x − 2) + m + 6

= (x² − x + 3)(x − 2)

Thực hiện phép chia A(x) = x³ − 3x² + 5x + m cho đa thức B(x) = x − 2.

Ta được thương là x² − x + 3 và số dư là m + 6.

Để A(x) chia hết cho B(x) thì số dư của phép chia phải bằng 0.

Khi đó m + 6 = 0

Û m = − 6

Vậy m = − 6 là giá trị m cần tìm.

Câu 34: Tính độ dài MN trên hình vẽ.

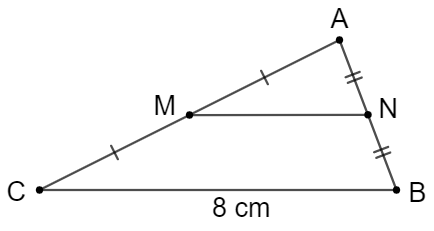
Lời giải:

Xét tam giác ABC có:

M là trung điểm của đoạn thẳng AB (AM = MC)

N là trung điểm của đoạn thẳng AB (AN = NB)

Þ MN là đường trung bình của tam giác ABC.

$\Rightarrow MN=\frac{1}{2}BC=\frac{1}{2}\cdot 8=4\left(cm\right)$.

Câu 35: Tìm tập hợp X sao cho $\left\{a;b\right\}\subset X\subset \left\{a;b;c;d\right\}$ .

Lời giải:

Tập X có thể xảy ra những trường hợp sau:

X = {a; b};

Hoặc X = {a; b; c};

Hoặc X = {a; b; d};

Hoặc X = {a; b; c; d}.

Câu 36:

a) Xác định các tập hợp X sao cho: $\left\{a;b\right\}\subset X\subset \left\{a;b;c;d;e\right\}$ .

b) Cho A = {1; 2}, B = {1; 2; 3; 4; 5}. Xác định các tập hợp X sao cho $A\cup X=B$ .

Lời giải:

a) Tập X có thể xảy ra những trường hợp sau:

X = {a; b};

Hoặc: X = {a; b; c}; X = {a; b; d}; X = {a; b; e};

Hoặc: X = {a; b; c; d}; X = {a; b; c; e}; X = {a; b; d; e};

Hoặc: X = {a; b; c; d; e}.

b) Để $A\cup X=B$  thì tập X có thể xảy ra những trường hợp sau:

X = {3; 4; 5};

Hoặc: X = {1; 3; 4; 5}; X = {2; 3; 4; 5};

Hoặc: X = {1; 2; 3; 4; 5}.

Câu 37:

a) Tìm m để đường thẳng y = (m + 2)x + m song song với đường thẳng y = 3x – 2.
b) Hãy vẽ đồ thị của hàm số $y=-\frac{1}{4}{x}^2$ .

Lời giải:

a) Để đường thẳng y = (m + 2)x + m song song với đường thẳng y = 3x − 2 thì:

$\left\{\begin{array}{l}m+2=3\\ m\ne -2\end{array}\right.\Rightarrow \left\{\begin{array}{l}m=1\\ m\ne -2\end{array}\right.\Rightarrow m=1$.

Vậy m = 1 là giá trị của m thỏa mãn yêu cầu bài toán.

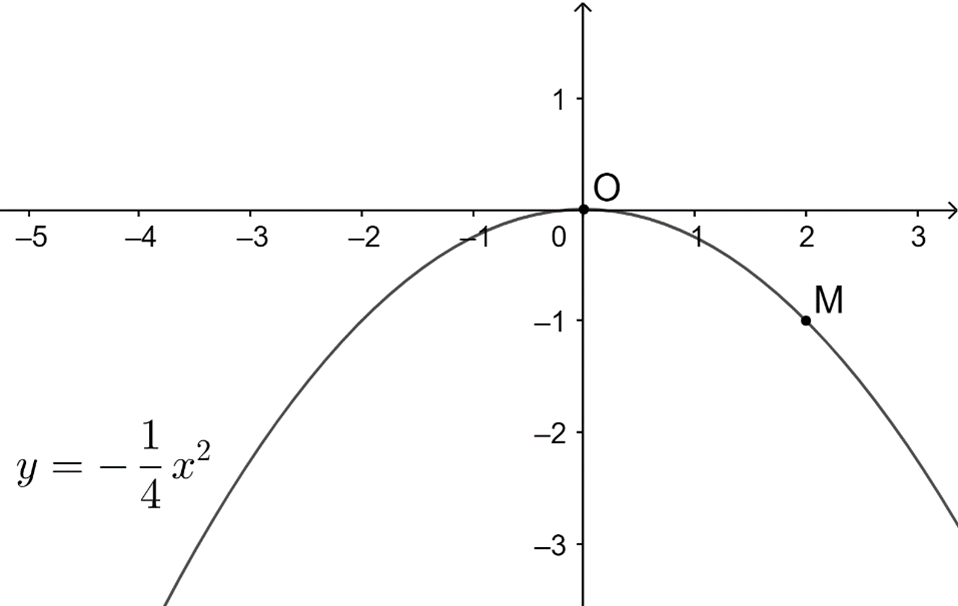
b) Đồ thị của hàm số $y=-\frac{1}{4}{x}^2$ .

• Với x = 0 Þ y = 0 nên đồ thị hàm số đi qua O(0; 0).

• Với x = 2 $\Rightarrow y=-\frac{1}{4}\cdot 2^2=-1$  nên đồ thị hàm số đi qua điểm M(2; −1).

Ta có đồ thị hàm số $y=-\frac{1}{4}{x}^2$  như sau:

Câu 38: Tìm m, n để đường thẳng y = mx + n song song với đường thẳng y = 3x + 2 và cắt trục hoành tại điểm có hoành độ là 2.

Lời giải:

Để y = mx + n song song với y = 3x + 2 thì $\left\{\begin{array}{l}m=3\\ m\ne 2\end{array}\right.$ .

Phương trình đường thẳng có dạng: y = 3x + n (n ≠ 2).

Do đường thẳng cắt trục hoành tại điểm có hoành độ bằng 2 nên

0 = 3.2 + n Þ n = −6

Vậy m = 3 và n = −6.

Câu 39: Kiểm tra rằng cặp số (x; y) = (2; −1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Lời giải:

• Thay x = 2, y = −1 vào phương trình 2x + y = 3, ta được:

$\left\{\begin{array}{l}VT=2.2+\left(-1\right)=3\\ VP=3\end{array}\right.\Rightarrow VT=VP$

Do đó (2; −1) là nghiệm của phương trình 2x + y = 3.

• Thay x = 2, y = −1 vào phương trình x – 2y = 4, ta được:

$\left\{\begin{array}{l}VT=2-2.\left(-1\right)=4\\ VP=4\end{array}\right.\Rightarrow VT=VP$

Do đó (2; −1) là nghiệm của phương trình x – 2y = 4.

Vậy cặp số (x; y) = (2; −1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Câu 40: 1 tấn bằng bao nhiêu tạ? $\frac{1}{5}$  tấn bằng bao nhiêu kg?

Lời giải:

1 tấn = 10 tạ = 1 000 kg.

Vậy $\frac{1}{5}$  (tấn) $=\frac{1}{5}\cdot 1000\left(kg\right)=200\left(kg\right)$ .

Câu 41: Một tổ công nhân có 8 người dự định làm xong 1 sân bóng chuyền trong 6 ngày nhưng sau đó người ta quyết định là xong sân bóng sớm hơn 2 ngày. Hỏi như vậy phải bổ sung thêm bao nhiêu công nhân?

Lời giải:

1 người làm xong sân trong số ngày là:

8 × 6 = 48 (ngày)

Sớm hơn 2 ngày thì làm xong sau:

6 − 2 = 4 (ngày)

Số công nhân để làm xong trong 4 ngày là:

48 : 4 = 12 (công nhân)

Vậy cần bổ sung số công nhân là:

12 − 8 = 4 (công nhân)

Đáp số: 4 công nhân.

Câu 42: Tìm hiệu của số lớn nhất có ba chữ số và số bé nhất có ba chữ số khác nhau

Lời giải:

Số lớn nhất có 3 chữ số là 999.

Số bé nhất có ba chữ số khác nhau là 102.

Suy ra hiệu của chúng là:

999 − 102 = 897.

Đáp số: 897.

Câu 43: Tìm hiệu của số lớn nhất có ba chữ số khác nhau và số bé nhất có ba chữ số khác nhau

Lời giải:

Số lớn nhất có ba chữ số khác nhau: 987.

Số bé nhất có ba chữ số khác nhau: 102.

Hiệu của số lớn nhất có ba chữ số khác nhau và số bé nhất có ba chữ số khác nhau là: 987 − 102 = 885.

Đáp số: 885.

Câu 44: Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên gồm 3 chữ số phân biệt.

A. 10;

B. 20

C. 60;

D. 12.

Lời giải:

Gọi số tự nhiên thỏa mãn đề bài là $\overline{abc}\left(a,b,c\in \left\{1;2;3;4;5\right\};a\ne b\ne c\right)$ .

Có 5 cách chọn a.

Có 4 cách chọn b.

Có 3 cách chọn c.

Số số lập được là: 5.4.3 = 60.

Vậy ta chọn đáp án C.

Câu 45: Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 2 chữ số khác nhau?

A. 25;

B. 9;

C. 20;

D. 10.

Lời giải:

Mỗi số có 2 chữ số khác nhau được lập từ 5 chữ số là chỉnh hợp chập 2 của 5.

$\Rightarrow A_5^2=20.$

Vậy ta chọn đáp án C.

Câu 46: Tính 155,7 : 45

Lời giải:

155,7 : 45 = 1 557 : 10 : 45 = 1 557 : 45 : 10

= 1 557 : 9 : 5 : 10 = 173 : 5 : 10

= 1730 : 10 : 5 : 10 = 1730 : 5 : 100

= 346 : 100 = 3,46.

Câu 47: Đặt tính rồi tính 155,9 : 45

Lời giải:

Thử lại: 45 × 3,4 + 2,9 = 155,9

$\begin{array}{c}\mathrm{155,9}\\ 209\\ 29\end{array}\begin{array}{l}45\\ \begin{array}{l}\mathrm{3,4}\\ \end{array}\end{array}$

Vậy 155,9 : 45 = 3,4 (dư 2,9).

Câu 48: 2(x − 1) = 7 + (−3)

Lời giải:

2(x − 1) = 7 + (−3)

Û 2(x − 1) = 4

Û x − 1 = 4 : 2

Û x − 1 = 2

Û x = 3.

Câu 49: Tìm x, biết:

a) $\left|x-\mathrm{1,7}\right|=\mathrm{2,3}$ .

b) $\left|x+\frac{3}{4}\right|-\frac{1}{3}=0$ .

Lời giải:

a) $\left|x-\mathrm{1,7}\right|=\mathrm{2,3}$

+ TH1: x − 1,7 = 2,3

Û x = 2,3 + 1,7

Û x = 4

+TH2: x − 1,7 = −2,3

Û x = −2,3 + 1,7

Û x = −0,6.

Vậy nghiệm của phương trình là x = 4 và x = −0,6.

b) $\left|x+\frac{3}{4}\right|-\frac{1}{3}=0$

$\iff \left|x+\frac{3}{4}\right|=\frac{1}{3}$.

+ TH1: $x+\frac{3}{4}=\frac{1}{3}$

$$\begin{gathered} \iff x=\frac{1}{3}-\frac{3}{4} \\ \iff x=-\frac{5}{12} \end{gathered}$$

+ TH2: $x+\frac{3}{4}=-\frac{1}{3}$

$\iff x=-\frac{13}{12}$.

Vậy $x=-\frac{5}{12}$  và $x=-\frac{13}{12}$  là nghiệm của phương trình.

Câu 50: Cho đường thẳng (d): y = x − 2. Điểm A nằm trên (d) có hoành độ và tung độ đối nhau sẽ có tọa độ là (a; b).

Khi đó, a.b = …

Lời giải:

Vì A có hoành độ và tung độ đối nhau nên a = − b (1)

Vì A nằm trên d nên b = a − 2 (2)

Thay (2) vào (1) ta được: a = − (a − 2)

Û a = − a + 2

Û a = 1

Suy ra b = − a = −1.

Vậy khi đó a.b = −1.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 4)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 5)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 6)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 7)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 8)