1500 câu hỏi ôn tập môn Toán có đáp án (Phần 88)

1500 câu hỏi ôn tập Toán (Phần 88)

Câu 1: Xe thứ nhất chở được 25 tấn hàng, xe thứ hai chở 35 tấn hàng, xe thứ ba chở bằng trung bình cộng 3 xe. Hỏi xe thứ 3 chở bao nhiêu tấn hàng?

Lời giải:

Gọi số hàng xe thứ 3 chở được là a tấn.

a = (25 + 35 + a) : 3

⇔ 3a = 25 + 35 + a

⇔ 2a = 60

⇔ a = 30 (tấn)

Vậy xe thứ 3 chở được 30 tấn hàng.

Câu 2: Một cửa hàng có 3,125 tấn gạo. Ngày thứ nhất bán đc 24%số gạo. Ngày thứ hai bán đc 32% số gạo còn lại. Hỏi ngày thứ hai cửa hàng bán được bao nhiêu ki lô gam gạo?

Lời giải:

Đổi 3,125 tấn = 3125 kg

Ngày thứ nhất bán được số gạo là:

3125 : 100 . 24 = 750 (kg)

Sau ngày thứ nhất cửa hàng còn lại số gạo là:

3125 – 750 = 2375 (kg)

Ngày thứ 2 cửa hàng bán được số kg gạo là:

2375 : 100 . 32 = 760 (kg)

Sau 2 ngày cửa hàng bán , còn lại số kg là:

2375 – 760 = 1615 (kg).

Câu 3: Một căn phòng hình chữ nhật có chiều rộng 6m, chiều dài gấp rưỡi chiều rộng. Người ta lát nền căn phòng đó bằng loại gạch vuông cạnh 3dm . Hỏi căn phòng đó lát nền hết bao nhiêu viên gạch ?

Lời giải:

Chiều dài của căn phòng đó là:

6 . 1,5 = 9 (m²)

Diện tích của căn phòng đó là:

6 . 9 = 54 (m²)

Diện tích của 1 viên gạch là:

3 . 3 = 9 (m²)

Đổi: 54 m² = 5400 dm

Cần số gạch để lát hết phòng đó là:

5400 : 9 = 600 viên gạch

Đáp số: 600 viên gạch.

Câu 4: Một lớp có 25% học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Tính số học sinh của lớp đó biết số học sinh trung bình là 5 em?

Lời giải:

Số học sinh trung bình chiếm số phần trăm số học sinh cả lớp là:

100% – 25% – 55% = 20% (số học sinh cả lớp)

Số học sinh của lớp đó là:

5 : 20 . 100 = 25(học sinh)

Đáp số: 25 học sinh.

Câu 5: Năm ngoái, mẹ đi chợ mua 5 gói bánh quy hết 100000 đồng. Năm nay vẫn số tiền đó mẹ mua được 4 gói bánh quy. Hỏi năm nay giá một gói bánh quy tăng hay giảm bao nhiêu phần trăm?

Lời giải:

Giá tiền 1 gói bánh quy năm ngoái là:

100000 : 5 = 20000 (đồng)

Giá tiền 1 gói bánh quy năm nay là:

100000 : 4 = 25000 (đồng)

Giá tiền 1 gói nay năm tăng số % là:

25000 : 20000 . 100 = 125% (tức là tăng 25%).

Câu 6: Một cửa hàng bán một chiếc xe đạp với giá 1495000 đồng thì được lãi 15% so với tiền vốn mua xe đạp đó.hỏi tiền vốn mua chiếc xe của cửa hàng đó là bao nhiêu?

Lời giải:

Số tiền lãi:

1495000 . 15% = 224250 (đồng)

Tiền vốn mua chiếc xe của cửa hàng đó:

1495000 – 224250 = 1270750 (đồng).

Câu 7: Phép chiếu xuyên tâm có đặc điểm gì?

Lời giải:

Phép chiếu xuyên tâm có ba đặc điểm cơ bản sau:

– Qua phép chiếu xuyên tâm, hình chiếu của một điểm là một điểm. Điểm thuộc mặt phẳng hình chiếu là điểm trùng với chính nó.

– Qua phép chiếu xuyên tâm, hình chiếu của một đường thẳng không đi qua tâm chiếu là một đường thẳng.

– Đường thẳng chiếu là đường thẳng đi qua tâm chiếu, có hình chiếu là một điểm. Mặt phẳng đi qua tâm chiếu gọi là mặt phẳng chiếu, có hình chiếu là một đường thẳng. Đặc biệt, tỉ số kép của bốn điểm thẳng hàng được bảo toàn bởi phép chiếu này.

Câu 8: Tìm số tự nhiên x biết 3(x + 1) + 25 chia hết cho 5 và 8 < x < 16.

Lời giải:

Ta có: 3(x + 1) + 25

Thấy 25 chia hết cho 5 nên suy ra: 3(x + 1) chia hết cho 5

Mà 3 không chia hết cho 5 nên x + 1 chia hết cho 5

Hay x + 1 ∈ B(5) = {0; 5; 10; 15; 20; …}

Mà 8 < x < 16 nên 9 < x + 1 < 17

Suy ra x + 1 ∈ {10; 15}

Vậy x ∈ {9; 14}.

Câu 9: Phân tích đa thức thành nhân tử: 5xy⁴ + 15x⁴y + 15x²y³ + 5x³y².

Lời giải:

5xy⁴ + 15x⁴y + 15x²y³ + 5x³y²

= 5xy(y³ + 3x³ + 3xy² + x²y )

= 5xy[(3x³ + 3xy²) + (y³ + x²y)]

= 5xy([3x(x² + y²) + y(y² + x²)]

= 5xy (3x + y)(x² + y²).

Câu 10: Có bao nhiêu cách sắp xếp 5 bạn nam và 2 bạn nữ thành 1 hàng dọc theo thứ tự bất kì?

Lời giải:

Số cách sắp xếp 5 bạn nam: 5! (cách)

Số cách sắp xếp 2 bạn nữ: 2! (cách)

Số cách sắp xếp cho 5 bạn nam và 2 bạn nữ: 2! (cách)

Số cách sắp xếp 5 bạn nam và 2 bạn nữ thành 1 hàng dọc theo thứ tự bất kì là:

5! . 2! . 2! = 480 (cách).

Câu 11: Cửa hàng lấy 1 thùng nước ngọt (24 lon)của đại lý phân phối với giá 192.000 đồng và bán lẻ với giá 10.000 đồng/ lon.

a) Hỏi khi bán hết 1 barrel nước ngọt thì cửa hàng thu được lãi bao nhiêu % so với giá gốc?
b) Trong đợt khuyến mãi, do đại lý phân phối giảm giá nên cửa hàng cũng giảm còn 9.500 đồng/ lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua 1 barrel nước ngọt với giá bao nhiêu?

Lời giải:

a) Khi bán lẻ 1 thùng thì bán được số tiền là:

10000 . 24 = 240000 (đồng)

Số tiền lãi của 1 thùng khi bán lẻ là:

240000 – 192000 = 48000 (đồng)

Tiền lãi chiếm số % giá gốc là:

48000 : 192000 . 100 = 25 (%)

b) Tổng số tiền bán được 1 thùng là;

9500 . 24 = 228000 (đồng)

Vì lãi suất như cũ là 25%

Vậy số tiền bán được chiếm số phần trăm so với giá gốc là

100% + 25% = 125%

Trong đợt này cửa hàng đã mua 1 barrel nước ngọt với giá là:

228000 : 125%= 182400 (đồng).

Câu 12: Mỗi tháng mẹ bạn Hà được nhận 7 000 000 đồng tiền lương, mẹ đã mua có thực phẩm cho gia đình hết 5 600 000 đồng. Hỏi mẹ là mua thực phẩm hết bao nhiêu phần trăm số tiền lương?

Lời giải:

Mẹ Hà mua thực phẩm hết số tiền lương là:

5600000 : 7000000 = 0,8 = 80%.

Câu 13: Một cửa hàng thời trang nhập 100 cái áo với giá vốn mỗi chiếc 200000 đồng. Chi phí vận chuyển là 1000000 đồng. Hỏi cửa hàng bỏ ra bao nhiêu tiền vốn để nhập 100 cái áo?

Lời giải:

Cửa hàng bỏ ra số tiền vốn để nhập 100 cái áo là:

100 . 200000 + 1000000 = 21000000 (đồng).

Câu 14: Người ta lấy ra 15kg gạo trong một bao gạo là 75% lượng gạo trong bao đó. Lúc đầu bao đó có bao nhiêu kilôgam gạo?

Lời giải:

Bao gạo đó có tổng số gạo là:

15 : 75 . 100 = 20 (kg).

Đáp số: 20 (kg).

Câu 15: Hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.

Lời giải:

Đáy bé hình thang là:

(24 – 1,2) : 2 = 11,4 (cm)

Đáy lớn hình thang là:

24 – 11,4 = 12,6 (cm)

Chiều cao hình thang là:

11,4 – 2,4 = 9 (cm)

Diện tích hình thang là:

(11,4 + 12,6) . 9: 2 = 108 (cm²).

Câu 16: Lãi suất tiết kiệm là 0,58% một tháng. Một người gửi tiết kiệm 6000000 đồng. Hỏi sau 1 tháng cả số tiền gửi và tiền lãi là bao nhiêu?

Lời giải:

Sau 1 tháng, số tiền lãi nhận được là:

6000000 . 0,58% = 34800 (đồng)

Sau 1 tháng, cả số tiền gửi và tiền lãi là:

6000000 + 34800 = 6034800 (đồng).

Câu 17: Tính diện tích hình thang có đáy bé bằng 40cm, chiều cao bằng 30% đáy bé và và bằng 20% đáy lớn.

Lời giải:

Chiều cao của hình thang là:

(40 : 100) . 30 = 12 (cm)

Đáy lớn của hình thang là:

(12 : 20) . 100 = 60 (cm)

Diện tích hình thang là:

(60 + 40) . 12 : 2= 600 (cm²)

Câu 18: Tính diện tích hình thang có đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy bé kém đáy lớn 12 dm.

Lời giải:

Chiều cao là:

50 : 80 . 100 = 62,5 (dm)

Đáy bé là :

50 – 12 = 38 (dm)

Diện tích hình thang là:

(50 + 38) . 62,5 : 2 = 2750 (dm²).

Câu 19: Tính diện tích hình thang có đáy lớn bằng 25 m, chiều cao bằng 80% đáy lớn, đáy bé bằng 90% chiều cao.

Lời giải:

Chiều cao hình thang là :

25 . 80 : 100 = 20 (m)

Đáy bé hình thang là :

20 . 90 : 100 = 18 (m)

Diện tích hình thang là :

( 25 + 20 ) . 18 : 2 = 405 (m²)

Câu 20: Xác định hệ số a và b để 2x² + ax + 5 chia hết cho x + 3 dư 41.

Lời giải:

Đặt f(x) = 2x² + ax + 5; g(x) = x + 3

Theo Bezout ta có:

f(–3) = 2(–3)² – 3a + 5 = 23 – 3a

Để f(x) chia g(x) dư 41 thì 23 – 3a = 41

Suy ra: a = –6.

Vậy a = –6.

Câu 21: Tính bằng cách thuận tiện nhất: 57 . 0,1 . 100 . (2,5 . 4 – 10).

Lời giải:

57 . 0,1 . 100 . (2,5 . 4 – 10)

= 57 . 0,1 . 100 . (10 – 10)

= 57 . 0,1 . 100 . 0

= 0.

Câu 22: Tính giá trị biểu thức: 140 : 2,8 – 2,3.

Lời giải:

140 : 2,8 – 2,3 = 50 – 2,3 = 47,7.

Câu 23: Một vườn cây có 840 cây, trong đó có 672 cây lấy gỗ và còn lại là cây ăn quả.

a) Số cây lấy gỗ chiếm bao nhiêu phần trăm số cây trong vườn?

b) Tìm tỉ số phần trăm giữa số cây ăn quả và số cây lấy gỗ?

Lời giải:

a) Số cây lấy gỗ chiếm số phần trăm số cây trong vườn là:

672 : 840 . 100 = 80%

b) Vườn cây đó có số cây ăn quả là:

840 – 672 = 168 (cây)

Tỉ số phần trăm giữa số cây ăn quả số cây lấy gỗ là:

168 : 672 . 100 = 25%.

Câu 24: Hình chữ nhật , hình bình hành, hình thang cân , hình vuông , hình thoi . Mỗi hình có bao nhiêu tâm đối xứng , trục đối xứng.

Lời giải:

* Hình chữ nhật:

– Hình chữ nhật có 1 tâm đối xứng, đó là giao điểm của hai đường chéo.

– Hình chữ nhật có 2 trục đối xứng (đó là đường trung trực của chiều dài và chiều rộng).

* Hình vuông:

– Hình vuông có 1 tâm đối xứng là giao điểm hai đường chéo.

– Hình vuông có 4 trục đối xứng là hai đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông.

– Hình vuông có 4 trục đối xứng.

* Hình bình hành:

– Hình bình hành có 1 tâm đối xứng là giao điểm hai đường chéo.

– Hình bình hành không có trục đối xứng.

* Hình thang cân:

– Hình thang cân có 1 trục đối xứng là đường thẳng đi qua trung điểm hai đáy của hình thang cân.

* Hình thoi:

– Hình thoi có hai trục đối xứng là hai đường chéo.

– Hình thoi có 1 tâm đối xứng là giao điểm hai đường chéo.

Câu 25: Tính bằng cách thuận tiện: 0,2468 + 0,08 . 0,4 . 12,5 . 2,5 + 0,7532.

Lời giải:

0,2468 + 0,08 . 0,4 . 12,5 . 2,5 + 0,7532

= 0,2468 + (0,08 . 12,5) . (0,4 . 2,5) + 0,7532

= 0,2468 + 1 . 1 + 0,7532

= 0,2468 + 1 + 0,7532

= 1 + (0,2468 + 0,7532)

= 1 + 1

= 2.

Câu 26: Tìm x biết: –125 + 2(5 – x) = –5.

Lời giải:

–125 + 2(5 – x) = –5

⇔ 2(5 – x) = –5 – (–125) = –5 + 125 = 120

⇔ 5 – x = 120 : 2

⇔ 5 –x = 60

⇔ x = 5 – 60

⇔ x = –55

Vậy x = –55.

Câu 27: Có bao nhiêu số tự nhiên chia hết cho 4 thoả mãn số đó nhỏ hơn 31,72 và lớn hơn 3,73 ?

Lời giải:

Gọi số cần tìm là x

Ta có: 3,73 < x < 31,72

Suy ra: x ∈ {4; 8; 12; 16; 20; 24; 28}

Vậy có 7 số tự nhiên thỏa mãn.

Câu 28: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào 1 bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách xếp cho 3 học sinh nữ ngồi kề nhau?

Lời giải:

Cho 3 bạn nữ là 1 nhóm nữ, xếp 3 bạn nữ có 3! cách

Sắp xếp nhóm nữ và 2 bạn nam vào 3 vị trí có 3! cách

Như vậy có tất cả 3!.3! = 36 cách.

Câu 29: Học sinh khối 5 của một trường tiểu học sinh hoạt động ngoài trời: Nếu chia thành các tổ, mỗi tổ 6 học sinh nam và 6 học sinh nữ thì còn thùa 20 học sinh nam. Nếu chia thành các tổ, mỗi tổ 7 học sinh nam và 5 học sinh nữ thì còn thừa 20 học sinh nữ. Hỏi khối 5 trường tiểu học đó có bao nhiêu học sinh nam ?

Lời giải:

Hiệu số học sinh nam giữa hai cách xếp là:

7 – 6 = 1 (học sinh nam)

Số tổ học sinh là:

20 : 1 = 20 (tổ)

Số học sinh nam là:

6 . 20 + 20 = 140 (học sinh nam)

Đáp số: 140 học sinh nam.

Câu 30: Một cây cau cao 9 m bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu?

Lời giải:

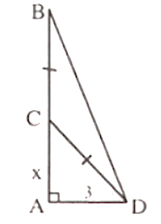
Giả sử AB là độ cao của cây cau, C là điểm gãy

Đặt AC = x (0 < x < 9)

Suy ra: CB = CD = 9 – x

Vì tam giác ACD vuông tại A nên AC² + AD² = CD²

⇔ x² + 3² = (9 – x)²

⇔ x² + 9 = 81 – 18x + x²

⇔ 18x = 72

⇔ x = 4

Vậy điểm gãy cách gốc 4 m.

Câu 31: Một cửa hàng nhập về 100 cái áo với giá vốn là 200 000 đồng mỗi cái,cửa hàng đã bán 60 cái áo, mỗi cái lời 25% so với giá mua, 40 cái áo còn lại lỗ 5% so với giá mua. Hỏi sau khi bán hết cửa hàng đã lời bao nhiêu tiền?

Lời giải:

Cửa hàng mua 100 cái áo hết số tiền là:

200 000 . 100 = 20 000 000 (đồng)

60 cái áo đầu tiên mỗi cái được bán với giá:

200 000 . (100% + 25%) = 250 000 (đồng)

60 cái áo đầu tiên cửa hàng bán được số tiền là:

250 000 . 60 = 15 000 000 (đồng)

40 cái áo còn lại mỗi cái được bán với giá:

200 000.(100% − 5%) = 190 000 (đồng)

40 cái áo còn lại cửa hàng bán được số tiền là:

190 000 . 40 = 7 600 000 (đồng)

Sau khi bán hết 100 cái áo cửa hàng thu được số tiền là:

15 000 000 + 7600000 = 22 600 000 (đồng)

Cửa hàng đã lời số tiền là:

22 600 000 – 20000000 = 2 600 000 (đồng).

Câu 32: Một người mua một chục bát có giá 40000 đồng. Người đó bán với giá 50000 đồng . Hỏi người đó được lãi bao nhiêu phần trăm so với tiền mua?

Lời giải:

Người đó lãi số tiền là: 50000 – 40000 = 10000 (đồng)

Người đó lãi số tiền so với số tiền vốn là: 10000 : 40000 = 0,25 = 25%.

Câu 33: Năm 2010 , gia đình bác Tám thu hoạch được 8 tấn thóc. Năm 2011 gia đình bác tám thu hoạch được 8,5 tấn thóc.

a) Hỏi so với năm 2010 năm 2011 số thóc mà gia đình bác tám thu hoạch tăng thêm bao nhiêu phần trăm?

b) Nếu so với năm 2011 năm 2015 số thóc cũng tăng thêm bấy nhiêu phần trăm thì năm 2015 gia đình bác Tám thu hoạch được bao nhiêu tấn thóc?

Lời giải:

a) So với năm 2010, năm 2011 số thóc mà gia đình bác Tám thu hoạch tăng thêm là:

8,5 – 8 = 0,58 (tấn)

Số với năm 2010, năm 2011 số thóc mà gia đình bác Tám thu hoạch tăng thêm số phần trăm là:

0,5 : 8 = 0,0625 = 6,25%

b) Nếu so với năm 2011, năm 2015 số thóc cũng tăng thêm 6,25% thì năm 2015 gia đình bác Tám thu hoạch được thêm số tấn thóc là:

8,5 . 6,25 : 100 = 0,53125 (tấn)

Vậy năm 2015, gia đình bác Tám thu hoạc được số tấn thóc là:

8,5 + 0,53125 = 9,03125 (tấn).

Câu 34: Tìm một số biết số đó cộng thêm 21 rồi nhân tổng đó với 165 thì được kết quả là 6270.

Lời giải:

Gọi số phải tìm là a

Theo bài ra ta có: (a + 21) . 165 = 6270

⇔ a + 21 = 6275 : 165

⇔ a = 38 − 21

⇔ a = 17

Vậy số phải tìm là 17.

Câu 35: Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau đúng hay sai?

Lời giải:

Mệnh đề sai.

Vì nếu hai tam giác bằng nhau thì sẽ dẫn đến diện tích bằng nhau. Nhưng ngược lại khi chúng có diện tích bằng nhau thì không thể suy ra chúng bằng nhau (ví dụ một tam giác vuông có 2 cạnh góc vuông là 3, 4 và 1 tam giác nhọn có đáy là 4, chiều cao là 3 thì diện tích của hai tam giác là bằng nhau bằng 6, nhưng hai tam giác này không thể bằng nhau vì một bên là tam giác vuông một bên là tam giác nhọn).

Câu 36: Chứng minh rằng: 35x – 14y + 2⁹ – 1 chia hết cho 7.

Lời giải:

Ta có 35x – 14y + 2⁹ – 1 = 35x – 14y + 511 = 7(5x – 2y + 73)

Ta thấy 7 ⋮ 7 nên 7(5x – 2y + 73) ⋮ 7 với mọi x, y.

Vậy 35x – 14y + 2⁹ – 1 chia hết cho 7.

Câu 37: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OC = 2cm. Tính AC ?

Lời giải:

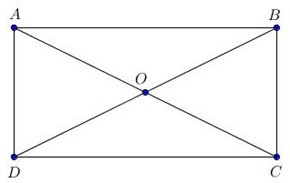
Vì ABCD là hình chữ nhật nên O là trung điểm của AC và BD

Suy ra: AC = 2OC = 2 . 2 = 4 (cm).

Câu 38: Cho x + 2y = 5. Tính giá trị biểu thức A = x² + 4y² – 2x + 10 + 4xy – 4y.

Lời giải:

A = x² + 4y² – 2x + 10 + 4xy – 4y

A = x² + (2y)² – 2x + 10 + 4xy – 4y

A = x² + (2y)² + 4xy – 2x + 10 – 4y

A = (x + 2y)² – 2(x + 2y) + 10

A = 5² – 2.5 + 10

A = 25 – 10 + 10

A = 25.

Câu 39: Nhân ngày 20/10, một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiết của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy thu ngân.

a) Chị Hoa không có thẻ thân thiết của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1.050.000đ. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?

b) Cô Hà có thẻ khách hàng thân thiết, cô mua một chiếc túi xách và nhận được một voucher trị giá 91.000đ. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?

Lời giải:

a) Chị Hoa phải trả số tiền là:

1050000.(1 − 30%) = 735000(đồng)

b) Giá chiếc túi đã giảm khi có thẻ khách hàng thân thiết là:

91000 : 10% = 910000 (đồng)

Giá chiếc túi ban đầu là:

910000 : (1 − 30%) = 1300000(đồng).

Câu 40: Tính giá trị biểu thức: – 87 + (–12) – (–487) + 512

Lời giải:

–87 + (–12) – (–487) + 512

= –87 – 12 + 487 + 512

= –99 + 999

= 900.

Câu 41: Trong một kì kiểm tra, có 42% học sinh không đạt môn nhảy xa, 52% không đạt môn đá cầu, trong đó 17% học sinh không đạt cả 2 môn, hãy tính % số học sinh đã đạt cả hai môn đó.

Lời giải:

Phần trăm số học sinh không đạt là:

52% + 42% − 17% = 77%

Coi số học sinh là 100%

Phần trăm số học sinh đạt là:

100% − 77% = 23%.

Câu 42: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I.
a. Chứng minh: AD//BM và tứ giác ADBM là hình thoi.
b. Gọi E là giao điểm AM và DC. Chứng minh: AE = EM.

Lời giải:

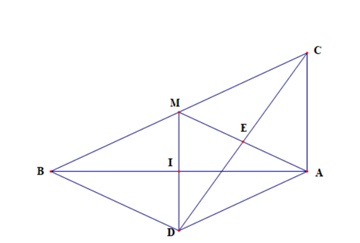
a) Xét tứ giác ADBM có I là trung điểm của hai đường chéo MD và AB

Suy ra ADBM là hình bình hành

Lại có AB ⊥ MD (do D là điểm đối xứng của M qua I)

Do đó ADBM là hình thoi

Suy ra AD // BM

b) Vì ADBM là hình thoi nên AM // BD

Ta có: CA ⊥ AB và MI ⊥ AB

Suy ra CA // MI (quan hệ từ vuông góc đến song song)

Xét tứ giác ADMC có CM // AD, MD // AC

Suy ra ADMC là hình bình hành

Mà AM cắt CD tại trung điểm E nên AE = EM

Vậy AE = EM.

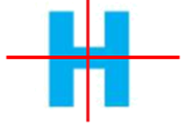
Câu 43: Hình chữ “H” có bao nhiêu trục đối xứng?

Lời giải:

Chữ "H" có 2 trục đối xứng.

Câu 44: Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:

P = x² + 5y² + 4xy + 6x + 16y + 32.

Lời giải:

P = x² + 5y² + 4xy + 6x + 16y + 32

⇔ P = x² + (4xy + 6x) + 5y² + 16y + 32

⇔ P = x² + 2x(2y + 3) + (2y + 3)² – (2y + 3)² + 5y² + 16y + 32

⇔ P = [x + (2y + 3)]² – 4y² – 12y – 9 + 5y² + 16y + 32

⇔ P = (x + 2y + 3)² + y² + 4y + 23

⇔ P = (x + 2y + 3)² + (y + 2)² + 19

Vì (x + 2y + 3)² ≥ 0 với mọi x, y ∈ R

(y + 2)² ≥ 0 với mọi y ∈ R

⇒ P = (x + 2y + 3)² + (y + 2)² + 19 ≥ 19 với mọi x, y ∈ R

Dấu "=" xảy ra khi và chỉ khi x + 2y + 3 = 0 và y + 2 =0

Suy ra, x = 1 và y = –2

Vậy P đạt giá trị nhỏ nhất bằng 19 tại x = 1 và y = –2.

Câu 45: Có bao nhiêu cách sắp ngẫu nhiên 10 học sinh gồm 2 học sinh 11A, 3 học sinh lớp 11B và 5 học sinh lớp 11C thành 1 hàng ngang sao cho không có học sinh nào cùng lớp đứng cạnh?

Lời giải:

Xếp 5 học sinh lớp 11C thành một hàng có 5! cách

∗TH1: Không có học sinh lớp 11A, 11B đứng cạnh nhau

Giữa 5 học sinh lớp 11C tạo ra 5 khoảng trống

C__C__C__C__C__

Số cách chọn 5 vị trí trống có 2 cách

(C__C__C__C__C__ hoặc __C__C__C__C__C)

Xếp 5 học sinh lớp 11A và 11B vào 5 khoảng trống có 5! cách

Có 2 cách chọn 5 vị trí trống

Trường hợp này có 5!.5!.2 = 28800

∗TH2: Có 1 cặp gồm 2 học sinh lớp 11A,11B đứng cạnh nhau

(C A B C A C B C B C)

Giữa 5 học sinh lớp 11C tạo ra 4 khoảng trống

C__C__C__C__C

Chọn 1 cặp A,B có: 2.3 cách

Đổi chỗ vị trí cho A,B trong cặp có 2 cách

Xếp cặp A,B và học sinh lớp 11A, 11B còn lại 4! cách

Thường hợp này có 5!.2.3.4!.2 = 34560

Vây số cách sắp xếp học sinh = 28800 + 34560 = 63630.

Câu 46: Phân tích đa thức thành nhân tử: –x² – 2xy – y².

Lời giải:

–x² – 2xy – y²

= –(x² + 2xy + y²)

= –(x + y)².

Câu 47: Biết 48 lít dầu nặng 36 kg. Một can chứa dầu nặng 30 kg. Biết cân nặng của can khi rỗng là 1,5 kg, số lít dầu chứa trong can đó là?

Lời giải:

1 lít dầu cân nặng là:

36 : 48 = 0,75 (kg).

Số dầu chứa trong can là:

(30 − 1,5) : 0,75 = 38 (lít).

Câu 48: Lớp 6A có 42 học sinh, lớp 6B có 54 học sinh và lớp 6C có 48 học sinh. Cô phụ trách đã xếp đều số học sinh của 3 lớp thành một số hàng như nhau. Tính số hàng nhiều nhất có thể xếp được.

Lời giải:

Vì số học sinh xếp đủ nên số hàng dọc là ước chung của số học sinh ba lớp Số hàng dọc nhiều nhất cũng là ước chung lớn nhất của số học sinh ba lớp .

Ta có:

54 = 2.3³

42 = 2.3.7

48 = 2⁴ .3

ƯCLN (54; 42; 48) = 2.3 = 6.

Vậy số hàng dọc nhiều nhất xếp được là 6 hàng.

Câu 49: Tìm y biết: 76,22 – y . 3 = 30,61 . 2.

Lời giải:

76,22 – y . 3 = 30,61 . 2

⇔ 76,22 – 3y = 61,22

⇔ 3y = 76,22 – 61,22

⇔ 3y = 15

⇔ y = 15 : 3

⇔ y = 5.

Vậy y = 5.

Câu 50: Tính giá trị biểu thức x + (–10) biết x = –28

Lời giải:

x + (–10) = –28 + –10 = –38

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: