1500 câu hỏi ôn tập môn Toán có đáp án (Phần 4)
Bộ 1000 câu hỏi ôn tập môn Toán có đáp án Phần 4 hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
1500 câu hỏi ôn tập Toán (Phần 4)
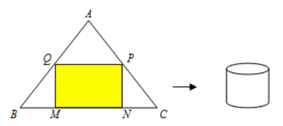
Lời giải:
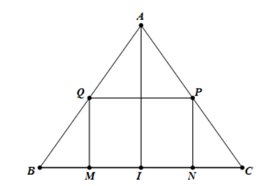
Gọi I là trung điểm của BC. Suy ra I là trung điểm của MN. Đặt MN=x, (0<x<90).
Khi đó ta có: MQAI=BMBI⇔MQ=√32(90−x). Gọi R là bán kính của hình trụ ⇒R=x2π.
Thể tích của khối trụ là: V=π(x2π)2√32(90−x)=√38π(−x3+90x2).
Xét f(x)=√38π(−x3+90x2), với 0<x<90. Suy ra
f'
Do đó
Lời giải: Sử dụng tổng cấp số nhân, ta có công thức sau:
Trong đó với N là số tiền vay, là lãi suất hàng tháng), a là số tiền trả hàng tháng và n là số tháng.
Khi đó:
Vậy anh A mất 18 tháng thì sẽ trả hết nợ cho ngân hàng.
Lời giải: Ta có hình vẽ sau:
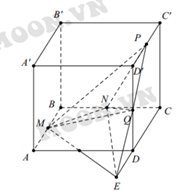
Khi đó ta có:
Do nên ta có:
Vì vậy
Câu 4: Cho các hình sau thì có bao nhiêu hình là đa diện lồi?
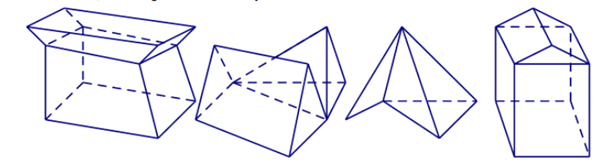
Lời giải: Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.
Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
Vậy theo định nghĩa trên thì chỉ có 1 hình là đa diện lồi.
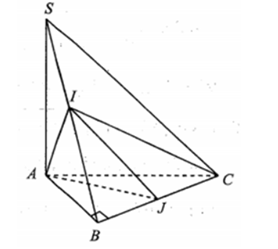
Lời giải: Do tam giác ABC vuông cân tại B nên ta có
Đồng thời do
Suy ra Mặt khác: (do J là trung điểm của BC).
Ta có:
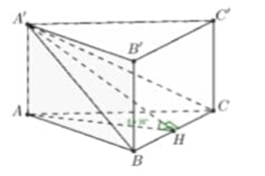
Câu 6: Cho hình lăng trụ đều ABC.A'B'C'. Biết rằng góc giữa (A'BC) và (ABC) là Tam giác A'BC có diện tích bằng 8. Tính thể tích của khối lăng trụ ABC.A'B'C'
Lời giải: Gọi H là trung điểm của BC. Đặt AB = a ta có:
Xét tam giác A'AH ta tìm được:
Suy ra
Thể tích của khối lăng trụ ABC.
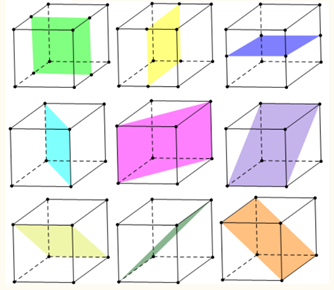
Câu 7: Hình lập phương có bao nhiêu mặt đối xứng?
Lời giải: Hình lập phương có 9 mặt đối xứng
Lời giải:
Xét hàm số f(x) = x3 – 3x2 – 9x + m trên đoạn [– 2; 4].
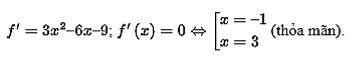
Ta có: f(– 2) = m – 2, f(– 1) = m + 5, f(3) = m – 27, f(4) = m – 20.
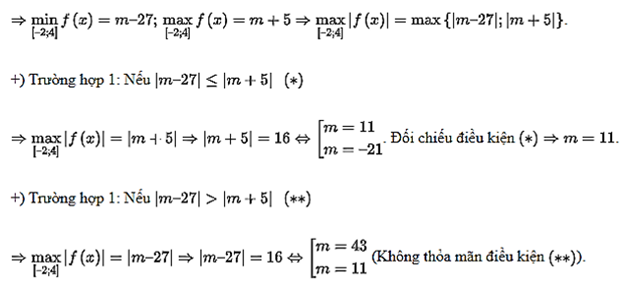
Vậy S = {11}. Do đó S có 1 phần tử.
Câu 9: với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là.
Lời giải: Ta có:
Để đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình: y' = 0 có 5 nghiệm phân biệt. Điều này tương đương với Đặt phải có 3 nghiệm phân biệt khác 0 và 2.
Ta có: tức là ta cần đi tìm giá trị của m để đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt.
Do đó ta khảo sát hàm số thì ta có được:
Vậy S tổng tất cả các giá trị của S là 6.
Câu 10: Đồ thị hàm số có bao nhiêu điểm cực trị?
Lời giải: Xét hàm số Tập xác định D = R
Ta xét đạo hàm bậc nhất: Khi đó ta có BBT sau:
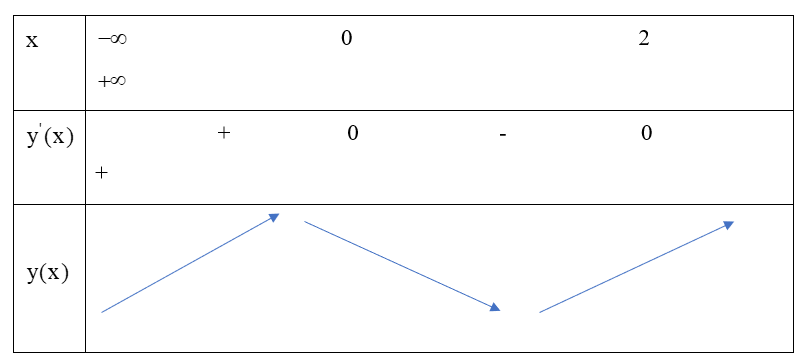
Hàm số là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy. Như vậy ta sẽ thu được đồ thị hàm số có dạng sau:
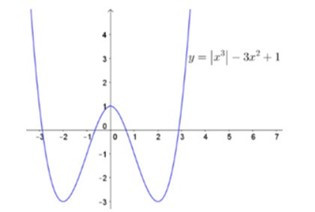
Lời giải:
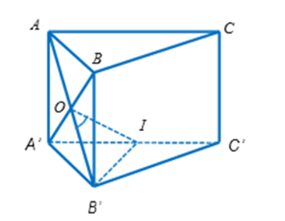
Gọi O là tâm của hình bình hành ABB'A' và I là trung điểm của A'C'. Ta có:
Mặt khác nên là tam giác đều.
Suy ra
Vì là hình lăng trụ tam giác đều nên tam giác AA'B' vuông tại A' và có
Thể tích của khối lăng trụ đã cho là:
Câu 12: Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a và O là tâm của đáy. Gọi M, N, P và Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và là điểm đối xứng của S qua O. Tính thể tích của khối chóp S'.MNPQ
Lời giải:
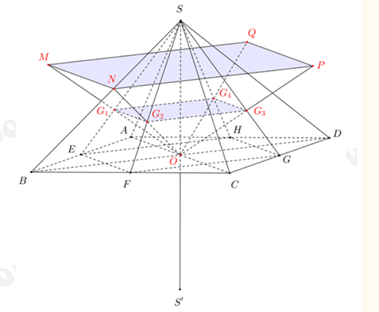
Gọi lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Ta có:
Mặt khác:
Vậy thể tích của khối chóp S'.MNPQ là:
Lời giải:
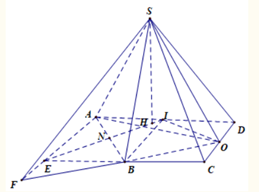
Gọi I, N là trung điểm của AD, AB. Gọi H là tâm đường tròn ngoại tiếp tam giác ABO, vì tam giác ABI đều nên H thuộc NI.
Kẻ HK vuông góc CD, dựng hình bình hành AECD. Gọi F là giao điểm của BO và AE.
Ta có: nên
Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, nên tam giác BIC và CID là các tam giác đều, do đó ta có:
Suy ra
Diện tích
Thể tích của khối chóp S. AFO là:
Diện tích tam giác SAF:
Vậy
Lời giải:
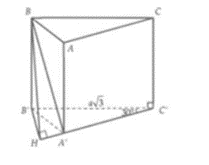
Ta có:
Mà
Vậy suy ra thể tích của khối lăng trụ đứng ABC.A'B'C' là:
Câu 15: Cho G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
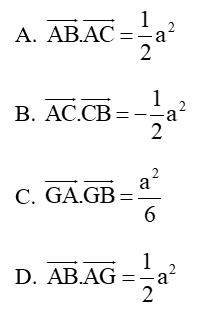
Lời giải: Đáp án C.
Dựa vào đáp án ta có nhận xét: Xác định góc nên
Tương tự ta cũng xác định là góc ngoài của góc C nên
Xác định góc của do đó
Tương tự cho ý đáp án D, ta ra kết quả là
Câu 16: Cho hình nón có thiết diện qua trục là tam giác đều. Gọi lần lượt là thể tích của khối cầu nội tiếp và nội tiếp hình nón đã cho. Tính tỉ số
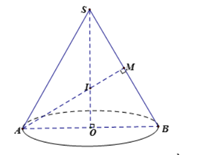
Lời giải: Giả sử cạnh của tam giác đều SAB bằng 1. Gọi thiết diện qua trục hình nón là tam giác đều SAB.
Gọi I là trọng tâm của tam giác đều SAB, khi đó I là tâm mặt cầu nội tiếp hình nón cũng là tâm mặt cầu ngoại tiếp hình nón.
Bán kính mặt cầu ngoại tiếp hình nón là:
Bán kính mặt cầu nội tiếp hình nón là:
Thể tích mặt cầu ngoại tiếp hình nón là:
Thể tích mặt cầu nội tiếp hình nón là:
Vậy
Lời giải: Gọi số tự nhiên có 6 chữ số đôi một khác nhau có dạng:
Sắp xếp cụm số 3, 4, 5 mà số 4 luôn đứng cạnh 3 và 5 thì ta có 2 cách sắp xếp: 345 và 543.
TH1: Nếu các cụm số 3, 4, 5 đứng đầu có các số tạo thành là: (số)
TH2: Nếu các cụm số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345.
Khi đó 3 chữ số còn lại có: cách chọn và sắp xếp.
Do đó ta có được các số tạo thành là: (số)
Áp dụng quy tắc cộng có: số thỏa mãn yêu cầu bài toán.
Lời giải: Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau từ tập A (không tính chữ số 0 đứng đầu) là: (số).
Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau mà số 3 và số 4 đứng cạnh nhau là: (số).
Xác suất cần tìm thỏa mãn bài toán là:
Lời giải:
Ta có: 0 + 6 = 2 + 4 = 1 + 5
Suy ra a, b, c, d, e, f ∈ {0; 1; 2; 4; 5; 6}
+) a khác 0 nên a có 5 cách, b có 1 cách.
+) c khác a và b nên c có 4 cách, d có 1 cách.
+) e khác a, b, c, d nên e có 2 cách, d có 1 cách.
Do đó có 5.4.2 = 40 cách.
Ta lại có: 0 + 5 = 2 + 3 = 1 + 4
Do đó có 40 cách.
Vậy tổng cộng có 40 + 40 = 80 số.
Câu 20: Cho hình hộp chữ nhật ABCD.A'B'C'D' có Tính diện tích mặt cầu ngoại tiếp hình hộp đã cho.
Lời giải:
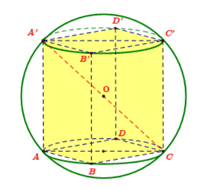
Gọi O là mặt cầu ngoại tiếp của hình hộp chữ nhật ABCD.A'B'C'D' .
Khi đó bán kính của hình hộp sẽ là:
Vậy diện tích của mặt cầu ngoại tiếp hình hộp là:
Lời giải:
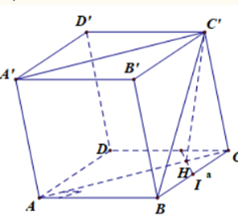
Do nên kẻ Do nên
(với I là trung điểm của BC).
Ta có:
Tam giác vuông tại H nên ta có:
Tam giác vuông ABC có
Vậy thể tích của lăng trụ đã cho là:
Câu 22: Số cách chia 12 phần quà giống nhau cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà.
Lời giải:
+ Chia trước cho mỗi học sinh một phần quà thì số phần quà còn lại là 9 phần quà.
+ Chia 9 phần quà cho 3 học sinh sao cho học sinh nào cũng có ít nhất một phần quà: Đặt 9 phần quà theo một hàng ngang, giữa các phần quà sẽ có 8 khoảng trống, chọn 2 khoảng trống trong 8 khoảng trống đó để chia 9 phần quà còn lại thành 3 phần quà mà mỗi phần có ít nhất một phần quà, có
+ Vậy tất cả có số cách chia là: (cách chia).
Lời giải: Cho 3 học sinh nam cầm tay nhau coi như là một người, cùng với 2 học sinh nữ xếp thành một hàng ngang, có 3! cách.
Ba học sinh nam có thể đổi chỗ cho nhau, có 3! cách.
Vậy theo quy tắc nhân sẽ có: cách xếp.
Lời giải:
B1: Số cách chọn ra 3 bạn nam trong 10 bạn nam là:
B2: Số cách chọn ra 2 bạn nữ trong 8 bạn nữ là:
B3: Áp dụng theo quy tắc nhân ta có số cách chọn ra 5 bạn thỏa mãn đề bài là:
Câu 25: Từ các chữ số 0, 1, 2, 3, 4, 5, có thể lập bao nhiêu số gồm 3 chữ số khác nhau và chia hết cho 9.
Lời giải: Gọi số cần lập có 3 chữ số đôi một khác nhau có dạng:
Theo giả thiết là các số này sẽ chia hết cho 9, do đó ta có:
Khi đó các số a, b, c thuộc các tập số và
+ TH1: Nếu các số a, b, c thuộc tập A.
Khi đó chữ số a có: 2 cách chọn; chữ số b có 2 cách và c có 1 cách chọn. Vậy ta có: 2.2.1=4 (số).
+ TH2: Nếu các số a, b, c thuộc tập B.
Khi đó a có 3 cách chọn, b có 2 cách và c có 1 cách chọn. Vậy ta có: 3.2.1 = 6 (số).
Áp dụng quy tắc cộng ta có các số tạo thành thỏa mãn bài toán là: 6 + 4 = 10 (số).
Lời giải: Đặt y = 23 xét số trong đó a; b; c; d; e đôi một khác nhau và thuộc tập {0; 1; y; 4; 5}.
Khi đó có 4 cách chọn a; 4 cách chọn b; 3 cách chọn c; 2 cách chọn d và 1 cách chọn e.
Theo quy tắc nhân có 4.4.3.2 = 96 số.
Khi ta hoán vị trong y ta được hai số khác nhau.
Vậy có tất cả: 96.2 = 192 số thỏa mãn yêu cầu bài toán.
Câu 27: Tính cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
Lời giải:
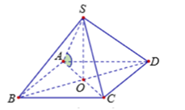
Gọi các cạnh của đáy ABCD đều có độ dài là a.
Vì chóp S. ABCD là chóp tứ giác đều, nên do đó ta có:
Gọi O là tâm của hình vuông ABCD thì ta có:
Suy ra ta có:
Xét tam giác SAO vuông tại O ta có:
Lời giải: Đồ thị hàm số có 2 điểm cực trị nằm về hai phía của Ox
cắt trục Ox tại 3 điểm phân biệt.
có 3 nghiệm phân biệt.
Ta có:
Để (C) cắt trục Ox tại 3 điểm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác 2.
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện trên.
Câu 29: Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng 2a. Biết Tính thể tích của khối hộp ABCD.A'B'C'D'
Lời giải:
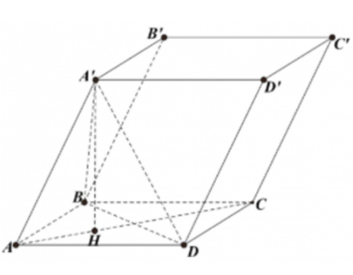
Từ giả thiết ta có các tam giác ABD, A'AD, A'AB là các tam giác đều.
Suy ra ta có: nên H là hình chiếu của A' trên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp tam giác đều ABD.
Do đó:
Vậy thể tích của khối hộp là:
Câu 30: Cho tam giác ABC, biết AB = 8, AC = 9, BC = 11. Gọi M là trung điểm của BC, N là điểm trên đoạn AC sao cho Hãy khai triển theo
Lời giải:
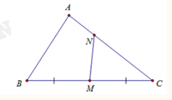
Ta có:
Vậy
Câu 31: Cho . Hãy so sánh P và
Lời giải:
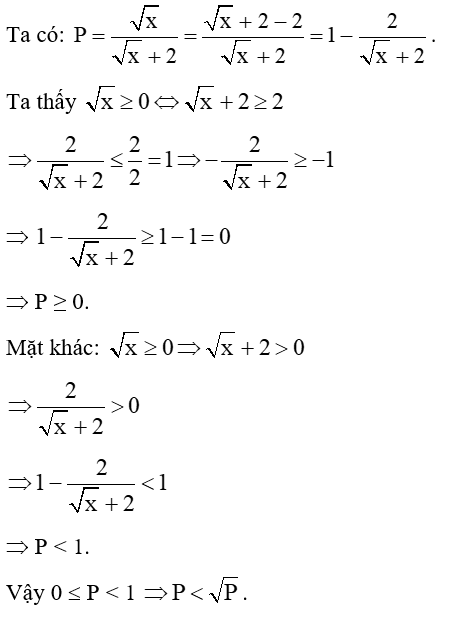
Câu 32: Cho , với x > 1. Hãy so sánh P và
Lời giải:
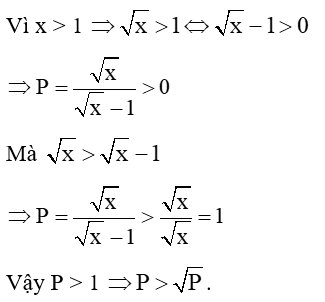
Lời giải:
Tổng mới giảm số đơn vị là:
19,1 − 7,4 = 11,7.
Do ở tổng mới số hạng thứ nhất bị giảm đi 4 lần nên số hạng thứ nhất còn lại 3 phần trên tổng 4 phần. Khi đó, số hạng thứ nhất là:
11,7 : 3 × 4 = 15,6.
Số hạng thứ hai là:
19,1 − 15,6 = 3,5.
Đáp số: Số hạng thứ nhất: 15,6; số hạng thứ hai là: 3,5.
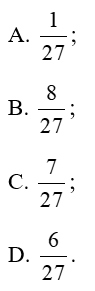
Lời giải:
Ta có: n(Ω) = 3.3.3 = 27.
Gọi A là: “Tổng số ghi trên ba tấm thẻ là 6”.
Để tổng số ghi trên ba tấm thẻ là 6 thì có các tổng sau:
1 + 2 + 3 = 6. Khi đó hoán vị 3 phần tử 1, 2, 3 ta được 3! = 6 (cách).
2 + 2 + 2 =6. Khi đó ta có 1 cách.
Do đó n(A) = 6 + 1 = 7.
Vậy .
Vậy ta chọn đáp án C.
Lời giải:
Số phần tử của không gian mẫu là .
Ta tính số cáchchonj ba phần tử khác nhau của tập hợp A sao cho ba phần tủ nhày là độ dài ba cạnh một tam giác.
Giả sử ba số cần chọn là x < y < z. Khi đó ta phải có x > z − y.
Đặt k = z − y; 1 £ k £ 49.
Với k = 1, ta có x Î {2; 3; …; 98}. Ta xét từng trường hợp như sau:
+ x = 2 các bộ số (y; z) lượt là (3; 4), (4; 5), …, (99; 100) có 97 bộ.
+ x = 3 các bộ số (y; z) lượt là (4; 5), (5; 6), …, (99; 100) có 96 bộ.
…
+ x = 8 chỉ có 1 bộ số (y; z) = (99; 100) thỏa mãn.
Do đó số bộ ba trong trường hợp này là .
Với k = 2, ta có x Î {3; 4; …; 97}. Ta xét từng trường hợp như sau:
+ x = 3 các bộ số (y; z) lượt là (4; 6), (5; 7), …, (98; 100) có 95 bộ.
…
+ x = 97 chỉ có 1 bộ số (y; z) = (98; 100) thỏa mãn.
Như vậy trường hợp này số bộ ba là .
Lập luận tương tự đến trường hợp k = 49 thì x = 50 và chỉ có một bộ số (y; z) thỏa mãn là (51; 100).
Vậy số cách chọn bộ ba số thỏa mãn yêu cầu là
Xác suất của biến cố cần tìm là .
Câu 36: Cho x Î ℕ. Hãy chứng minh x2 + 1 không chia hết cho 4.
Lời giải:
+ TH1: Nếu x chẵn, ta đặt: x = 2k, với k Î ℕ.
Þ x2 + 1 = 4k2 + 1 không chia hết cho 4 .
+ TH2: Nếu x chẵn, ta đặt: x = 2k + 1, với k Î ℕ.
Þ x2 + 1 = 4k2 + 4k + 2 = 4k(k + 1) + 2.
Vì 4k(k + 1) ⋮ 4 Þ 4k(k + 1) + 2 chia cho 4 dư 2
Þ 4k(k + 1) + 2 không chia hết cho 4.
Vậy với x Î ℕ thì x2 + 1 không chia hết cho 4.
Câu 37: Trong các mệnh đề sau, mệnh đề nào sai?
A. ∃ n Î ℕ, n2 + 11n + 2 chia hết cho 11;
B. ∃ n Î ℕ, n2 + 1 chia hết cho 4;
C. Tồn tại số nguyên tố chia hết cho 5;
Lời giải:
+ Xét đáp án A. Khi n = 3 thì giá trị của n2 + 11n + 2 bằng 44, chia hết cho 11
Nên đáp án A đúng.
+ Xét đáp án B. Khi n = 2k, k Î ℕ.
Þ n2 + 1 = 4k2 + 1 không chia hết cho 4, k Î ℕ.
Khi n = 2k + 1, với k Î ℕ.
Þ x2 + 1 = 4k2 + 4k + 2 = 4k(k + 1) + 2, k Î ℕ.
Nên đáp án B sai.
+ Xét đáp án C. Tồntaij số nguyên tố 5 chia hết cho 5 nên đáp án C đúng.
+ Xét đpas án D. Phương trình 2x2 − 8 = 0
Û x2 = 4
Û x = ± 2 Î ℤ.
Nên đáp án D đúng.
Vậy ta chọn đáp án B.
Câu 38: Cho tam giác ABC vuông tại A có đường cao AH.
Lời giải:
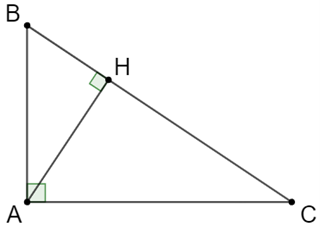
Do ∆ABC là tam giác vuông tại A nên:
Mặt khác theo định lý Pytago thì:
BC2 = AB2 + AC2
.
Do đó ta có đpcm.
Câu 39: Cho 4 điểm O, A, B, C sao cho .
Chứng minh: A, B, C thẳng hàng.
Lời giải:
Vậy 3 điểm A, B, C thẳng hàng.
Lời giải:
Gọi số đội viên là a.
Ta có: a chia 2, 3, 4, 5 đểu dư 1 Þ a − 1 chia hết cho 2, 3, 4, 5
Þ a − 1 Î BC(2, 3, 4, 5).
Mà BCNN(2, 3, 4, 5) = 60
Þ a − 1 Î B(60) = {0; 60; 120; 180; 240; …}
Vì a − 1 thuộc khoảng 100 đến 150
Þ a − 1 = 120
Þ a = 121
Vậy liên đội đó có 121 đội viên.
Câu 41: Phân tích đa thức thành nhân tử:
Lời giải:
a) 7x2y − 14xy2 + 21x2y2
= 7xy(x − 2y + 3xy).
b) 2x(x − y) + 3y(y − x)
= 2x(x − y) − 3y(x − y)
= (x − y)(2x − 3y).
c) 6x(x − 3) + 2x − 6
= 6x(x − 3) + 2(x − 3)
= (x − 3)(6x + 2)
= 2(x − 3)(3x + 1).
d) 4x(x − y)2 + 3x − 3y
= 4x(x − y)2 + 3(x − y)
= (x − y)[4(x − y) + 3]
= (x − y)(4x − 4y + 3).
Câu 42: Tính: (14xy2 + 21x2y − 7x3) : 7x
Lời giải:
(14xy2 + 21x2y − 7x3) : 7x
= 7x.(2y2 + 21x2y − 7x2) : 7x
= 2y2 + 21x2y − 7x2.
Câu 43: Đọc tên góc, đỉnh, và các cạnh của góc trong các hình vẽ sau:
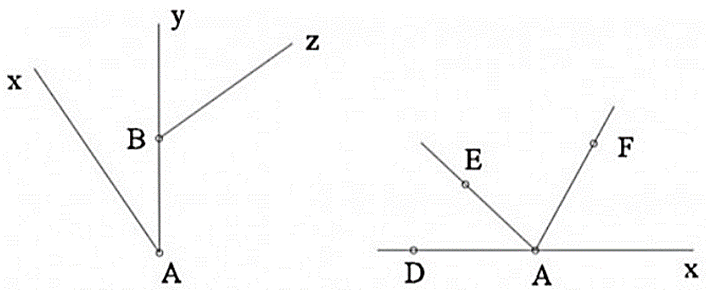
Lời giải:

Câu 44: Đọc tên góc, đỉnh và các cạnh của góc trong Hình 85 và Hình 86.
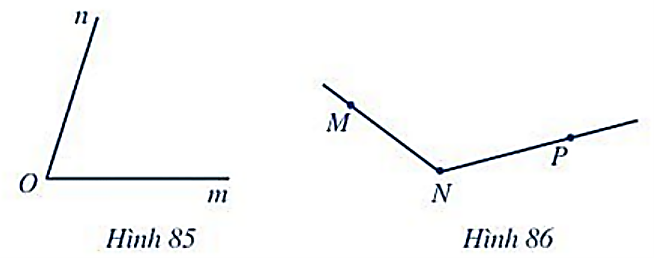
Lời giải:
Hình 85. Góc có đỉnh là O, cạnh của góc là Om và On.
Hình 86. Góc có đỉnh là N, cạnh của góc là NM và NP.
Câu 45: Phân tích thành nhân tử: x3 + y3 + z3 − 3xyz.
Lời giải:
x3 + y3 + z3 − 3xyz = (x + y)3 − 3xy(x + y) + z3 − 3xyz
= [(x + y)3 + z3] − [3xy(x + y) + 3xyz]
= (x + y + z)[(x + y)2 − (x + y)z + z2] − 3xy(x + y + z)
= (x + y + z)(x2 + 2xy + y2 − xz − yz + z2 − 3xy)
= (x + y + z)(x2 + y2 + z2 − xy − xz − yz).
Lời giải:
Vì M(1; −6) là điểm cực đại của đồ thị hàm số nên x = 1 là nghiệm của y' = 0, đồng thời M thuộc đồ thị
Thay vào y' ta có:
Þ 6x2 + 6x − 12 = 0
Û 6x2 − 6x + 12x − 12 = 0
Û 6x(x − 1) + 12(x − 1) = 0
Û 6(x − 1)(x + 2) = 0
Suy ra nghiệm còn lại là x = −2 là điểm CT của hàm số
Þ y = 21
Suy ra tọa độ điểm CT của đồ thị hàm số là N(−2; 21).
Lời giải:
Gọi 3 số hạng lần lượt là x, x + d, x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 27 nên ta có: x + x + d + x + 2d = 27
Û 3x + 3d = 27
Û x + d = 9 Û d = 9 – x.
Tổng các bình phương của chúng là 293 nên suy ra:
x2 + (x + d)2 + (x + 2d)2 = 293
Û x2 + (x + 9 − x)2 + (x + 18 − 2x)2 = 293
Û x2 + 92 + (18 − x)2 = 293
Û x2 + 81 + 324 − 36x + x2 = 293
Û 2x2 − 36x + 112 = 0
Û x2 − 18x + 56 = 0
Û (x − 14)(x − 4) = 0
• TH1: Với x = 14, d = −5 thì 3 số hạng cần tìm là 14; 9; 4;
• TH2: Với x = 4, d = 5 thì 3 số hạng cần tìm là 4; 9; 14.
Vậy 3 số hạng liên tiếp cần tìm là 4; 9; 14 hoặc 14; 9; 4.
Lời giải:
Gọi 3 số hạng2 lần lượt là x; x + d; x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 15 nên ta có:
x + x + d + x + 2d = 15
Û 3x + 3d = 15 Û x + d = 5
Û d = 5 – x.
Tổng các bình phương của chúng là 83 nên suy ra
x2 + (x + d)2 + (x + 2d)2 = 83
Û x2 + (x + 5 − x)2 + (x + 10 − 2x)2 = 83
Û x2 + 52 + (10 − x)2 = 83
Û x2 + 25 + 100 − 20x + x2 = 83
Û 2x2 − 20x + 42 = 0
Û x2 − 10x + 21 = 0
Û (x − 3)(x − 7) = 0
• TH1: Với x = 3, d = 2 thì 3 số hạng cần tìm là 3; 5; 7;
• TH2: Với x = 7, d = −2 thì 3 số hạng cần tìm là 7; 5; 3.
Vậy 3 số hạng liên tiếp cần tìm là 3; 5; 7 hoặc 7; 5; 3.
Câu 49: Nêu tính chất đối xứng của hình vuông, hình chữ nhật, hình thoi, hình bình hành.
Lời giải:
• Hình bình hành:
Hình bình hành có bốn cạnh; những cạnh đối nhau thì song song và bằng nhau.
• Hình thoi:
Hình thoi có bốn cạnh bằng nhau; những cạnh đối diện song song với nhau.
• Hình chữ nhật:
Hình chữ nhật có bốn cạnh và bốn góc vuông. Những cạnh đối nhau thì song song và bằng nhau.
• Hình vuông:
Hình vuông có bốn cạnh bằng nhau và bốn góc vuông.
Câu 50: Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.
Lời giải:
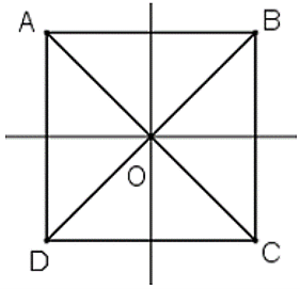
• Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.
• Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.
• Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.
Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 5)
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 6)
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 7)
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Tổng hợp các đề đọc - hiểu có đáp án chi tiết
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)
