1500 câu hỏi ôn tập môn Toán có đáp án (Phần 24)

1500 câu hỏi ôn tập Toán (Phần 24)

Câu 1: Cho ∆ABC đều, cạnh AB = BC = AC = a = 6, kẻ đường cao từ A xuống cắt với BC tại H, tính chiều cao AH.

Lời giải:

Thay a = 6, ta được: $h=AH=a\frac{\sqrt{3}}{2}=6\frac{\sqrt{3}}{2}=3\sqrt{3}$ .

Câu 2: Cho biểu thức $P=\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}-\frac{\sqrt{x}-3}{2-\sqrt{x}}-\frac{\sqrt{x}-2}{\sqrt{x}+3}\right)$ . Tìm giá trị của x để P < 1.

Lời giải:

Ta có:

$$\begin{gathered} P=\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}-\frac{\sqrt{x}-3}{2-\sqrt{x}}-\frac{\sqrt{x}-2}{\sqrt{x}+3}\right) \\ =\frac{-3}{2-\sqrt{x}} \end{gathered}$$

Để $P<1\iff \frac{-3}{2-\sqrt{x}}<1\iff 1+\frac{3}{2-\sqrt{x}}>0$

$\iff \frac{2-\sqrt{x}+3}{2-\sqrt{x}}>0\iff \frac{5-\sqrt{x}}{3-\sqrt{x}}>0$

TH1: $5-\sqrt{x}>0$ và $3-\sqrt{x}>0$

$\iff \sqrt{x}<5$ và $\sqrt{x}<0\iff \sqrt{x}<3\iff 0\le x<9$

TH2: $5-\sqrt{x}<0$  và $3-\sqrt{x}<0$

$\iff \sqrt{x}>5$ và $\sqrt{x}>3$

$\iff \sqrt{x}>5\iff x>25$.

Câu 3: Tìm x biết: x + 12 = – 5 – x.

Lời giải:

x + 12 = – 5 – x

⟺ 2x = – 17 ⟺ $x=-\frac{17}{2}$ .

Vậy $x=-\frac{17}{2}$ .

Câu 4: Cho $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$  và $\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0$ . Chứng minh rằng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ .

Lời giải:

Ta có:

+) $$\begin{gathered} \frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\iff \frac{ayz+bxz+cxy}{xyz}=0 \\ \iff ayz+bxz+cxy=0 \end{gathered}$$

+)$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\iff {\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)}^2=1$

$$\begin{gathered} \iff \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{xz}{zc}\right)=1 \\ \iff \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{ayz+bxz+cxy}{abc}\right)=1 \end{gathered}$$

$\iff \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ (đpcm).

Câu 5: Cho hàm số $y=\frac{2x+7}{x+2}$ có đồ thị (C). Hãy chọn mệnh đề sai:

A. Có đạo hàm $y^{\text{'}}=\frac{-3}{{\left(x+2\right)}^2}$ .

B. Hàm số có tập xác định là $D=R\backslash \left\{0\right\}$ .

C. Đồ thị cắt trục hoành tại điểm $A\left(-\frac{7}{2};0\right)$ .

D. Hàm số nghịch biến trên ℝ.

Lời giải:

Chọn D

Hàm số có tập xác định là $D=ℝ\backslash \left\{-2\right\}$ , đáp án B đúng.

$y=\frac{2x+7}{x+2}\Rightarrow \frac{-3}{{\left(x+2\right)}^2}<0\forall x\in D$

Hàm số nghịch biến trên (–∞; –2) và (2; +∞).

Câu 6: Cho α là góc tù và sinα – cosα = $\frac{4}{5}$ . Giá trị của M = sinα – 2cosα là ?

Lời giải:

Vì α là góc tù nên $\sin \alpha =\sqrt{1-{\cos }^2\alpha }$ .

Do đó, sin α – cos α = $\frac{4}{5}$

$$\begin{gathered} \iff \sqrt{1-{\cos }^2\alpha }-\cos \alpha =\frac{4}{5} \\ \iff \sqrt{1-{\cos }^2\alpha }=\cos \alpha +\frac{4}{5} \\ \iff \left\{\begin{array}{c}1-{\cos }^2\alpha ={\left(\cos \alpha +\frac{4}{5}\right)}^2\\ \cos \alpha \ge -\frac{4}{5}\end{array}\right. \\ \iff \left\{\begin{array}{c}50{\cos }^2\alpha +40\cos \alpha -9=0\\ \cos \alpha \ge -\frac{4}{5}\end{array}\right. \\ \iff \left\{\begin{array}{c}\left[\begin{array}{c}\cos \alpha =\frac{-4+\sqrt{34}}{10}\\ \cos \alpha =\frac{-4-\sqrt{34}}{10}\end{array}\right.\\ \cos \alpha \ge -\frac{4}{5}\end{array}\right. \\ \iff \cos \alpha =-\frac{4+\sqrt{34}}{10} (do \alpha tù) \end{gathered}$$

⇒ m = sin α – 2cos α = (sin α – cos α) – cos α

= $\frac{4}{5}+\frac{4+\sqrt{34}}{10}=\frac{12+\sqrt{34}}{10}$ .

Câu 7: Giải phương trình: $\sqrt{4x^2+5x+1}-2\sqrt{x^2-x+1}=9x-3$ .

Lời giải:

Đặt $\sqrt{4x^2+5x+1}=a;\sqrt{x^2-x+1}=b$  (a, b ≥ 0).

Ta có: $a^2-4b^2=4x^2+5x+1-4\left(x^2-x+1\right)=9x-3$ .

Khi đó từ phương trình đã cho ta suy ra a – 2b = $a^2-4b^2$

⇔ a – 2b = (a – 2b)(a + 2b)

⇔ (a – 2b)(1 – a – 2b) = 0

$\iff \left[\begin{array}{l}a=2b\\ a=1-2b\end{array}\right.$

TH1: a = 2b 

⇒ $\sqrt{4x^2+5x+1}=2\sqrt{x^2-x+1}\Rightarrow 9x=3\Rightarrow x=\frac{1}{3}$

TH2: a = 1 – 2b

$$\begin{gathered} \Rightarrow \sqrt{4x^2+5x+1}=1-2\sqrt{x^2-x+1} \\ \iff 4x^2+5x+1=1-4\sqrt{x^2-x+1}+4x^2-4x+4 \\ \iff 4\sqrt{x^2-x+1}=4-9x \\ \iff \left\{\begin{array}{l}4-9x\ge 0\\ 16x^2-16x+16=16-72x+81x^2\end{array}\right. \\ \iff \left\{\begin{array}{l}x\le \frac{4}{9}\\ 65x^2-56x=0\end{array}\right.\iff \left\{\begin{array}{l}x\le \frac{4}{9}\\ x\left(65x-56\right)=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x\le \frac{4}{9}\\ \left[\begin{array}{l}x=0\\ x=\frac{56}{65}\end{array}\right.\end{array}\right.\iff x=0 \end{gathered}$$

Thử lại ta thấy $x=\frac{1}{3}$  thỏa mãn phương trình đã cho.

Vậy $x=\frac{1}{3}$  là nghiệm của phương trình.

Câu 8: Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng $a\sqrt{2}$ . Tính thể tích của khối chóp S.ABC ?

Lời giải:

$$\begin{gathered} AM=\frac{\sqrt{3}}{2};AO=\frac{\sqrt{3}}{3};SO=\frac{\sqrt{15}}{3};S_{△}=\frac{a^3\sqrt{15}}{4} \\ \Rightarrow V=\frac{a^3\sqrt{15}}{12} \end{gathered}$$

Câu 9: Cho ∆ADC vuông tại a có đường cao AH, $\widehat{D}=65°$ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song với AD, trên Cx lấy điểm B sao cho CB = DA. Tính khoảng cách từ B đến AD, độ dài đoạn BD và diện tích tam giác ABD.

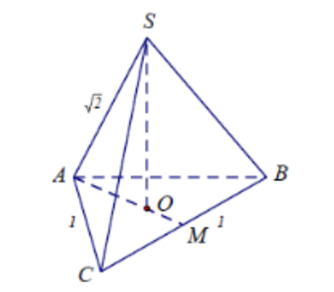
Lời giải:

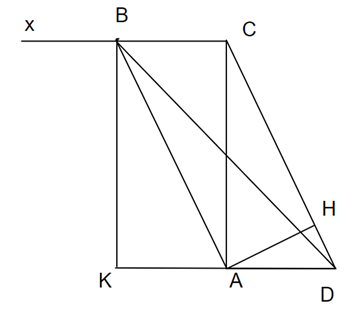
Kẻ BK ⊥ AD

Xét ∆ADC $(\widehat{A}=90°):\widehat{ADC}=65°\Rightarrow \widehat{ACD}=25°$

Khi đó: $CA=\frac{AH}{\sin \widehat{C}}=\frac{3}{\sin 25°}$

Dễ thấy BCAK là hình chữ nhật $\Rightarrow BK=AC=\frac{3}{\sin 25°}\left(cm\right)$ và BC = AK

⟹ DA = AK (= BC) ⇒ DK = 2DA

Ta có: $DA=\frac{AH}{\sin \widehat{CDA}}=\frac{3}{\sin 25°}\left(cm\right)$

$DK=2DA=\frac{6}{\sin 25°}\left(cm\right)$

Áp dụng định lí Pytago vào ∆BKD vuông tại K có $B{K}^2+K{D}^2=B{D}^2$

$$\begin{gathered} \iff {\left(\frac{3}{\sin 25°}\right)}^2+{\left(\frac{6}{\sin 25°}\right)}^2=B{D}^2 \\ \iff B{D}^2=\frac{45}{{\sin }^{2}25°} \\ \iff BD=\frac{3\sqrt{5}}{\sin 25°}\left(cm\right) \end{gathered}$$

Ta có

$$\begin{gathered} S_{ABD}=S_{BKD}-S_{BAK} \\ =\frac{BK.KD}{2}-\frac{AK.BK}{2} \\ =\frac{BK}{2}(KD-AK) \\ =\frac{BK.AD}{2} \\ =\frac{\frac{3}{\sin 25°}.\frac{3}{\sin 25°}}{2} \\ =\frac{18}{\sin 25°}\left(c{m}^2\right) \end{gathered}$$

Câu 10: Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h, $\widehat{SBA}=\alpha$ .

Lời giải:

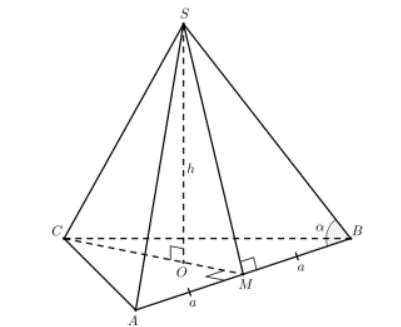
Gọi O là trọng tâm ∆ABC và M là trung điểm AB. Đặt AB = 2a (a > 0)

Vì O cũng là tâm đường trong ngoại tiếp ∆ABC nên SO ⊥ (ABC)

Mặt khác, vì ∆SAB cân tại S nên SM ⊥ AB

⇒ ∆SMB vuông tại M ⇒ SM = MB. tan? = atan? (1).

Ngoài ra, $OM=\frac{1}{3}CM=\frac{1}{3}.\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

∆SOM vuông tại O ⇒ SM = $\sqrt{S{O}^2+O{M}^2}=\sqrt{h^2+\frac{a^2}{3}}\left(2\right)$

Từ (1) và (2) ⇒?tan? = $\sqrt{h^2+\frac{a^2}{3}}\Rightarrow 3a^2.{\tan }^2\alpha =3h^2+a^2\Rightarrow a^2.(3{\tan }^2\alpha -1)=3h^2$

$\Rightarrow a^2=\frac{3h^2}{3{\tan }^2\alpha -1}\Rightarrow S_{ABC}=\frac{{\left(2a\right)}^2\sqrt{3}}{4}=a^2\sqrt{3}=\frac{3h^2\sqrt{3}}{3{\tan }^2\alpha -1}$

Vậy $V=\frac{1}{3}.SO.S_{ABC}=\frac{1}{3}.h.\frac{3h^2\sqrt{3}}{3{\tan }^2\alpha -1}=\frac{h^3\sqrt{3}}{3{\tan }^2\alpha -1}$ .

Câu 11: Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 60°. Tính thể tích hình chóp ?

Lời giải:

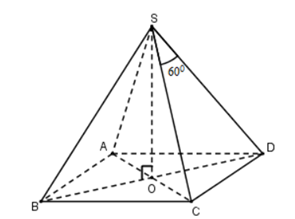
Gọi O = AC ∩ BD

Vì chóp S.ABCD đều nên SO ⊥ (ABCD)

Đặt SA = SB = SC = SD = a

∆SCD có: SC = SD; $\widehat{CSD}=60°\Rightarrow \Delta SCD$ đều ⇒ CD = SC = SD = a

⇒ Hình vuông cạnh ABCD cạnh a ⇒ AC = BD = $a\sqrt{2}\Rightarrow OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$

SO ⊥ (ABCD) ⇒ SO ⊥ OC ⇒ ∆SOC vuông tại O

$\Rightarrow SO=\sqrt{S{C}^2-O{C}^2}\Rightarrow h=\sqrt{a^2-\frac{a^2}{2}}=\frac{a\sqrt{2}}{2}\Rightarrow a=h\sqrt{2}$

$\Rightarrow S_{ABCD}=a^2={\left(h\sqrt{2}\right)}^2=2h^2$

Vậy $V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}h.2h^2=\frac{2h^3}{3}$ .

Câu 12: Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau:

Bước 1: x ← x + y

Bước 2: y ← x – y

Bước 3: x ← x – y

Lời giải:

Bước 1: Gán biến x = x + y

Bước 2: Gán biến y = x (bước 1) – y = x + y – y = x.

Bước 3: Gán biến x = x (bước 1) – y (bước 2) = (x + y) – x = y.

Kết quả của thuật toán là x = y và y = x.

Câu 13: Viết chương trình nhập số nguyên dương n. Kiểm tra n có phải là số nguyên tố hay không ?

– Input: 3

– Output: 3 là số nguyên tố

Lời giải:

Dựa vào định nghĩa của số nguyên tố chúng ta sẽ có cách giải như sau:

– Bước 1: Nhập vào n

– Bước 2: Kiểm tra nếu n < 2 thì kết luận n không phải là số nguyên tố

– Bước 3: Lặp từ 2 tới (n – 1), nếu trong khoảng này tồn tại số mà n chia hết thì kết luận n không phải là số nguyên tố, ngược lại n là số nguyên tố.

Câu 14: Cho 2 điểm A(3; 0), B(0; 4). Phương trình đường tròn (C) có bán kính nhỏ nhất nội tiếp ∆OAB là ?

Lời giải:

Phương trình đường thẳng AB là: $\frac{x}{3}+\frac{y}{4}=1\iff 4x+3y-12=0$

Giả sử đường tròn (C) có tâm I(a; b).

Đường trong (C) nội tiếp ∆OAB, suy ra (C) có bán kính nhỏ nhất và tiếp xúc Ox, Oy, AB

⇒ R = d(I, Ox) = d(I, Oy) = d(I, AB)

$\Rightarrow R=\left|b\right|=\left|a\right|=\frac{\left|4a+3a-12\right|}{5}\iff 5\left|a\right|=\left|7a-12\right|$

TH1: Nếu a = b, ta có $\left|a\right|=\frac{\left|4a+3a-12\right|}{5}\iff 5\left|a\right|=\left|7a-12\right|$

$\iff \left[\begin{array}{c}5a=7a-12\\ 5a=12-7a\end{array}\right.\iff \left[\begin{array}{c}a=6\\ a=1\end{array}\right.$

TH2: Nếu a – b, ta có $\left|a\right|=\frac{\left|4a-3a-12\right|}{5}\iff 5\left|a\right|=\left|a-12\right|$

$\iff \left[\begin{array}{c}5a=a-12\\ 5a=12-a\end{array}\right.\iff \left[\begin{array}{c}a=-3\\ a=2\end{array}\right.$

Vì (C) có bán kính nhỏ nhất nên chọn R = $\left|a\right|=1$

Suy ra (C) có tâm I(1; 1) và R = 1 ⇒ (C): ${\left(x-1\right)}^2+{\left(y-1\right)}^2=1$

$\iff x^2+y^2-2x-2y+1=0$.

Câu 15: Giải phương trình: $(x^2-5x+1)(x^2-4)=6{(x-1)}^2$

Lời giải:

Đặt $x^2-5x+1=a;x-1=b\Rightarrow x^2-4=a+5b$

PT đã cho trở thành: $a(a+5b)=6b^2$

$$\begin{gathered} \iff a^2+5ab-6b^2=0 \\ \iff a(a-b)+6b(a-b)=0 \\ \iff (a+6b)(a-b)=0 \end{gathered}$$

Xét 2 trường hợp:

TH1: a + 6b = 0

$$\begin{gathered} \iff x^2-5x+1+6(x-1)=0 \\ \iff x^2+x-5=0 \\ \Rightarrow x=\frac{-1\pm \sqrt{21}}{2} \end{gathered}$$

TH2: a – b = 0

$$\begin{gathered} \iff x^2-5x+1-(x-1)=0 \\ \iff x^2-6x+2=0 \\ \Rightarrow x=3\pm \sqrt{7} \end{gathered}$$

Câu 16: Cho các số từ 1 đến 9. Hãy điền các số này vào các ô vuông, sao cho tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau.

Lời giải:

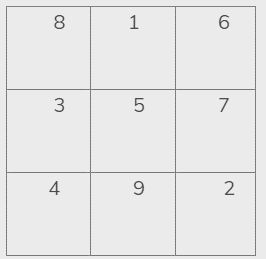
Bước 1: Xác định tổng

– Tổng các số từ 1 đến 9 là: 1 + 2 +....+ 9 = 45

– Vì 3 ô cộng lại đều bằng nhau nên: Tổng 3 ô là 45 : 3 = 15

Bước 2: Lấy 15 : 3 = 5 suy ra ô trung tâm phải là 5

Bước 3: Chỉ cần nghĩ ra 2 số cộng lại bằng 10 (vì đều cộng với số 5): 10 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6

Bước 4: Điền vào các ô theo cặp số.

Câu 17: Vẽ bản đồ tư duy hình vuông.

Lời giải:

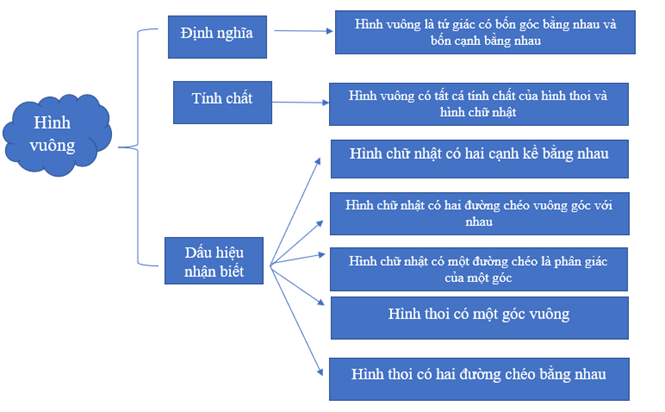
Câu 18: Vẽ bản đồ tư duy hình chữ nhật

Lời giải:

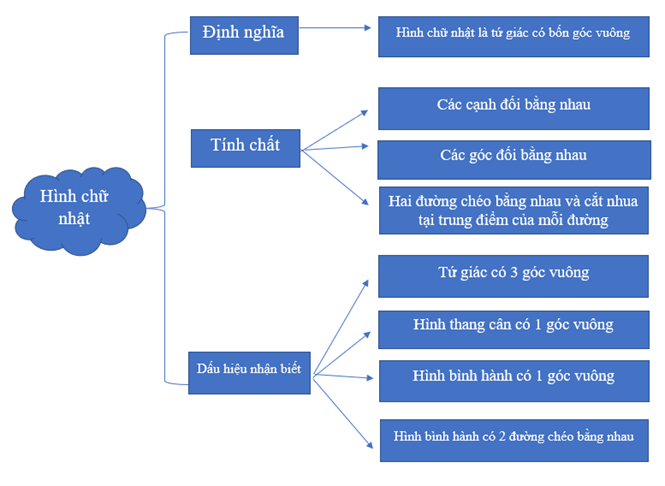
Câu 19: Tìm các số nguyên x, y thỏa mãn: $5x^2-4xy+y^2=169$ .

Lời giải:

$$\begin{gathered} 5x^2-4xy+y^2=169 \\ \iff x^2+{(2x-y)}^2={13}^2=144+25 \end{gathered}$$

$\iff x=12$ và 2x – y = 5 hoặc 2x – y = –5 ⇒ y = 21 hoặc y = 29 hoặc x = 5 và 2x – y = 12 hoặc 2x – y = –12 ⇒ y = –2 hoặc y = 22

Vậy chúng ta có 4 cặp số (x; y) thỏa mãn là (12; 21); (12; 29); (5; –12); (5; 22).

Câu 20: Cho ∆ABC, tìm vị trí điểm I sao cho $2\overrightarrow{IA}-3\overrightarrow{IB}-\overrightarrow{IC}=\overrightarrow{0}$ .

Lời giải:

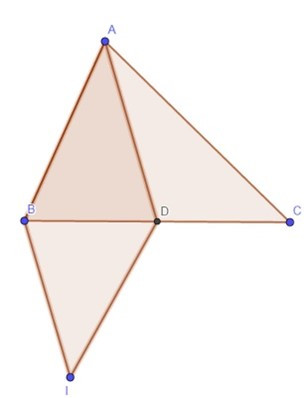
Ta có:

$$\begin{gathered} 2\overrightarrow{IA}-3\overrightarrow{IB}-\overrightarrow{IC}=\overrightarrow{0}\iff 2\overrightarrow{IA}-2\overrightarrow{IB}=\overrightarrow{IB}+\overrightarrow{IC} \\ \iff 2\overrightarrow{BA}=2\overrightarrow{ID}\iff \overrightarrow{BA}=\overrightarrow{ID} \end{gathered}$$

⇒ ABIJ là hình bình hành.

Câu 21: Một thùng đựng 39,75 kg đường, người ta lấy ra 10,5 kg rồi lại lấy tiếp 5 kg đường nữa. Số đường trong thùng còn lại là ?

Lời giải:

Số đường còn lại trong thùng là: 39,75 – 10,5 – 5 = 24,25 (kg).

Câu 22: Một cửa hàng ngày thứ nhất bán được 35,5 mét vải, ngày thứ hai bán gấp đôi ngày thứ nhất và kém ngày thứ ba 3 mét. Hỏi cả ba ngày cửa hàng đó bán được bao nhiêu mét vải ?

Lời giải:

Ngày thứ 2 cửa hàng đó bán được số mét vải là: 35,5 x 2 = 71 (m)

Ngày thứ 3 cửa hàng đó bán được số mét vải là: 71 + 3 = 74 (m)

Cả 3 ngày của hàng đó bán được số mét vải là: 35,5 + 71 + 74 = 180,5 (m).

Câu 23: Hoàn thiện chương trình dưới đây, chương trình nhập từ bàn phím 3 số thực a, b, c đưa ra thông điệp “Cả 3 số đều dương” nếu cả 3 số đều dương.

Lời giải:

a = float(input(“a=”))

b = float(input(“b=”))

c = float(input(“c=”))

if (a > 0) and (b > 0) and (c > 0):

print(“Cả ba số đều dương”)

Câu 24: Một của hàng bán vật liệu xây dựng có 127,5 tạ xi măng. Buổi sáng cửa hàng bán được $\frac{1}{5}$  lượng xi măng đó, buổi chiều bán được $\frac{1}{5}$  lượng xi măng còn lại. Hỏi cả sáng và chiều của hàng đó bán được bao nhiêu tạ xi măng ?

Lời giải:

Buổi sáng bán được số tạ xi măng là: 127,5 × $\frac{1}{5}$  = 25,5 (tạ xi măng)

Số tạ xi măng còn lại sau buổi sáng là: 127,5 – 25,5 = 102 (tạ xi măng)

Số tạ xi măng buổi chiều bán là: 102 × $\frac{1}{5}$  = 20,4 (tạ xi măng)

Số tạ xi măng buổi sáng và buổi chiều bán được là: 25,5 + 20,4 = 45,9 (tạ xi măng).

Câu 25: Đổi 123 phút = .......... giờ ...........phút ?

Lời giải:

123 phút = 2 giờ 3 phút

Câu 26: ab + a + b = 95. Tìm ab ?

Lời giải:

Ta có: ab + a + b = 95

a × 10 + b + a + b = 95

a × 11 + b x 2 = 95

aa + b × 2 = 95 

Vì 95 là số lẻ, b × 2 là số chẵn nên aa là số lẻ.

Ta có aa = 11, 33, 55, 77, 99

Để b là số có 1 chữ số thì b × 2 cao nhất là: 9 × 2 = 18

Ta có: 95 – 11 = 84,95 – 33 = 62, 95 – 55 = 40,95 – 77 = 18,95 – 99 = –5

Trong các giá trị tìm được, chỉ có 95 – 77 mới không vượt qua 18 và là số tự nhiên.

Vậy a = 7, b = 9.

Thử lại: 79 + 7 + 9 = 95.

Câu 27: Cho ∆ABC có AB = 2, AC = 3, $\widehat{BAC}=60°$ . Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn $\overrightarrow{AD}=\frac{7}{12}\overrightarrow{AC}$ . Tính $\overrightarrow{AB}.\overrightarrow{AC}$ .

Lời giải:

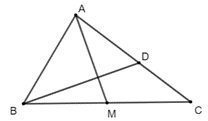
Ta có: $\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.\cos (\overrightarrow{AB},\overrightarrow{AC})$

$=AB.AC.\cos \widehat{BAC}=\mathrm{2.3.}\cos 60°=3$

Câu 28: Cho ∆ABC có AB = 6 cm, AC = 3 cm, $\widehat{BAC}=60°$ , M là điểm thỏa mãn $\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$ . Tính độ dài đoạn AM.

Lời giải:

Áp dụng định lí côsin ta được:

$$\begin{gathered} B{C}^2=A{B}^2+A{C}^2-2AB.AC.\cos \widehat{BAC} \\ \Rightarrow B{C}^2=6^2+3^2-\mathrm{2.6.3.}\cos 60°\Rightarrow B{C}^2=27 \\ \Rightarrow BC=3\sqrt{3}cm \end{gathered}$$

$\Rightarrow A{B}^2=B{C}^2+A{C}^2$⇒ ∆ABC vuông tại C

Mặt khác: $\overrightarrow{MB}+2\overrightarrow{MC}=0\Rightarrow CM=\frac{1}{3}BC=\sqrt{3}cm$

Áp dụng định lý Pytago ta được:

$$\begin{gathered} AM{}_2=A{C}^2+C{M}^2 \\ \Rightarrow AM=\sqrt{A{C}^2+C{M}^2}=\sqrt{9+3} \\ \Rightarrow AM=2\sqrt{3}cm \end{gathered}$$

Câu 29: Cho ∆ABC vuông tại A, kẻ đường cao AH. Gọi I, J là trung điểm của AH và HC. Chứng minh rằng: BI ⊥ AJ.

Lời giải:

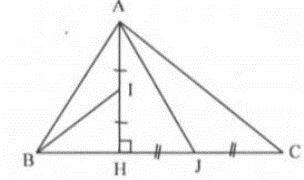
Ta có: $\overrightarrow{\text{AJ}}=\frac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{AC}\right);\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BH}\right)$

$$\begin{gathered} \overrightarrow{AJ}.\overrightarrow{BI}=\frac{1}{4}\left(\overrightarrow{AH}+\overrightarrow{AC}\right)\left(\overrightarrow{BA}+\overrightarrow{BH}\right)=\frac{1}{4}\left(\overrightarrow{AH}.\overrightarrow{BA}+\overrightarrow{AH}.\overrightarrow{BH}+\overrightarrow{AC}.\overrightarrow{BA}+\overrightarrow{AC}.\overrightarrow{BH}\right) \\ =\frac{1}{4}\left(\overrightarrow{AH}.\overrightarrow{HA}+0+0+\overrightarrow{HC}.\overrightarrow{BH}\right)=\frac{1}{4}\left(-A{H}^2+BH.HC\right) \end{gathered}$$

Vì ∆ABC vuông tại A nên: $A{H}^2=HB.HC$

Do đó: $\overrightarrow{AJ}.\overrightarrow{BI}=0\iff AJ\perp BI$ .

Câu 30: Lớp 5A có số học sinh giỏi bằng $\frac{1}{3}$ số học sinh cả lớp. Số học sinh khá bằng $\frac{3}{7}$  số học sinh cả lớp. Số học sinh trung bình bằng $\frac{1}{6}$  số học sinh cả lớp và còn lại 3 em học sinh kém. Hỏi lớp 5A có bao nhiêu học sinh giỏi?

Lời giải:

Tổng số phần là: $\frac{1}{3}+\frac{3}{7}+\frac{1}{6}=\frac{13}{14}$

Như vậy 3 học sinh kém chiếm: $1-\frac{13}{14}=\frac{1}{14}$  (học sinh cả lớp)

Số học sinh của lớp 5A là: $3:\frac{1}{14}=42$  (học sinh).

Câu 31: Trên 1 giá sách có 60 quyển sách. Biết số $\frac{1}{6}$ sách giáo khoa bằng $\frac{2}{3}$ số sách tham khảo. Tính số sách mỗi loại ?

Lời giải:

Ta có $\frac{1}{6}$ SKG = $\frac{2}{3}$ STK ⇒ $\frac{2}{12}$ SGK =  $\frac{2}{3}$ STK ⇒ STK = $\frac{3}{12}$ SGK = $\frac{1}{4}$ SGK

Sách giáo khoa là: 60 : (4 + 1) x 4 = 48 sách

Sách tham khảo là: 60 – 48 = 12 sách.

Câu 32: Cho $f\left(x\right)=\left(m^2-3m+2\right)x^2+2(2-m)x-2\left(1\right)$ . Tìm m để f(x) = 0 có 2 nghiệm dương phân biệt.

Lời giải:

$f\left(x\right)=\left(m^2-3m+2\right)x^2+2(2-m)x-2\left(1\right)$

Cho f(x) = 0. Để f(x) có 2 nghiệm dương phân biệt.

$$\begin{gathered} \left\{\begin{array}{c}a\ne 0\\ {\Delta }^{\text{'}}>0\\ P>0\\ S>0\end{array}\right.\iff \left\{\begin{array}{c}{m}^2-3m+2\ne 0\\ {\left(2-m\right)}^2-\left(m^2-3m+2\right)\left(-2\right)>0\\ \frac{2}{m^2-3m+2}>0\\ \frac{-4+2m}{m^2-3m+2}>0\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne 2;m\ne 1\\ 4-4m+m^2+2m^2-6m+4>0\\ m^2-3m+2>0\\ 1<m<2;m>2\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne 2;m\ne 1\\ 3m^2-10m+8>0\\ m<1;m>2\\ 1<m<2;m>2\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne \mathrm{2,}m\ne 1\\ m<\frac{4}{3},m>2\\ m<1;m>2\\ 1<m<2;m>2\end{array}\right. \\ \iff \left[\begin{array}{c}m<1\\ m>2\end{array}\right. \end{gathered}$$

Để f(x) = 0, f(x) có 2 nghiệm dương phân biệt

⇒ m ∈ (–∞; 1) ∪ (2; +∞).

Câu 33: Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường trong (O) lấy 1 điểm C sao cho AC < BC. Tiếp tuyến tại C của đường tròn (O) cắt Ax, By lần lượt tại E và F.

a. Chứng minh EF = AE + BF

c. BC cắt Ax tại D. Chứng minh $A{D}^2=DC.DB$

Lời giải:

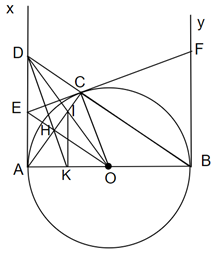
a. Theo tính chất tiếp tuyến của đường tròn: $\left\{\begin{array}{c}EA=EC\\ FC=FB\end{array}\right.$

$\Rightarrow EC+CF=EA+BF\Rightarrow EF=AE+BF$

b. Xét ∆ABC có OA = OB = OC (bán kính)

⇒ ∆ABC vuông tại C ⇒ AC ⊥ BC

Xét ∆DAB vuông tại A có AC là đường cao

$\Rightarrow A{D}^2=DC.DB$(Hệ thức lượng).

Câu 34: Chứng minh bất đẳng thức: $\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge 9$ .

Lời giải:

Áp dụng BĐT Cô–si cho vế trái ta có $\left\{\begin{array}{c}a+b+c\ge 3\sqrt[3]{abc}\\ \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge 3\sqrt[3]{\frac{1}{abc}}\end{array}\right.$

$$\begin{gathered} \Rightarrow \left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge 3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}} \\ \Rightarrow \left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge 9\sqrt[3]{\frac{abc}{abc}} \end{gathered}$$

$\Rightarrow \left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge 9$ (điều phải chứng minh).

Câu 35: Giải phương trình $x^2-2nx-5=0$ . Biết số nguyên dương n thỏa mãn $C_n^{n-1}+C_5^n=9$ .

Lời giải:

Xét phương trình: $C_n^{n-1}+C_5^n=9$ ⟺ n = 4

Với n = 4 thì phương trình trở thành: $x^2-8x-5=0$

Suy ra phương trình có 2 nghiệm $x=4\pm \sqrt{21}$ .

Câu 36: Hiệu của 2 số bằng 0,14. Tìm 2 số đó, biết rằng 5 lần số lớn trừ đi số bé thì được 18,1.

Lời giải:

4 lần số lớn là: 18,1 – 0,14 = 17,96

Số lớn là: 17,96 : 4 = 4,49

Số bé là: 4,49 – 0,14 = 4,35.

Câu 37: Một vòi nước chảy vào cái bể không có nước trong 2h. Giờ đầu vòi chảy được $\frac{1}{4}$ bể, giờ sau chảy được $\frac{1}{6}$ bể. Người ta đã dùng lượng nước $\frac{1}{3}$ bể. Hỏi lượng nước chiếm mấy phần bể ?

Lời giải:

Sau 2h vòi chảy được: $\frac{1}{4}+\frac{1}{6}=\frac{5}{12}$ (bể)

Sau khi dùng nước, trong bể còn số phần chiếm nước là: $\frac{5}{12}-\frac{1}{3}=\frac{1}{12}$ (bể).

Câu 38: Tìm nghiệm âm lớn nhất của phương trình $\sin x+\cos x=1-\frac{1}{2}\sin 2x$ .

Lời giải:

Phương trình $\sin x+\cos x=1-\frac{1}{2}\sin 2x$  có nghĩa x ∈ ℝ ⟺ D = ℝ.

Ta có: $\sin x+\cos x=1-\frac{1}{2}\sin 2x$ ⟺ sinx + cosx +sinxcosx – 1 = 0 (1)

Đặt t = sinx +cosx, $\left(\left|t\right|\le \sqrt{2}\right)$ . Ta có sinxcosx = $\frac{t^2-1}{2}$

⇒ (1) ⟺ $t+\frac{t^2-1}{2}-1=0\iff t^2+2t-3=0\iff \left[\begin{array}{c}t=1\\ t=-3\end{array}\right.$

Do $\left|t\right|\le \sqrt{2}$ nên t = 1

Với t = 1, ta có t = sinx + cosx = $\sqrt{2}\sin \left(x+\frac{\pi }{4}\right)=1\iff \sin \left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}=\sin \frac{\pi }{4}$

$\iff \left[\begin{array}{c}x+\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \iff x=k2\pi \\ x+\frac{\pi }{4}=\frac{3\pi }{4}+k2\pi \iff x=\frac{\pi }{2}+k2\pi \end{array}\right.,k\in \mathbb{Z}$

Vậy nghiệm âm lớn nhất của phương trình là $x=-\frac{3\pi }{2}$

Câu 39: Trong hệ tọa độ Oxy, cho 2 điểm A(2; 3); B(4; –1). Giao điểm của đường thẳng AB với trục tung tại M, đặt $\overrightarrow{MA}=k\overrightarrow{MB}$ , giá trị của k là ?

Lời giải:

Gọi $M(x_M;y_M)$

Vì M ∈ Oy ⇒ M(0; )

Ta có:

$$\begin{gathered} \overrightarrow{MA}=(2-0;3-y_M)=(2;3-y_M) \\ \overrightarrow{MB}=\left(4-0;-1-y_M\right)=\left(4;-1-y_M\right)\Rightarrow k\overrightarrow{MB}=\left(4k;-1k-y_{M}k\right) \end{gathered}$$

Khi đó: $\overrightarrow{MA}=k\overrightarrow{MB}$

$$\begin{gathered} \iff \left\{\begin{array}{c}2=4k\\ 3-y_M=-1k-y_{M}k\end{array}\right. \\ \iff \left\{\begin{array}{c}k=\frac{1}{2}\\ 3-y_M=-1k-y_{M}k\end{array}\right. \\ \iff \left\{\begin{array}{c}k=\frac{1}{2}\\ 3-y_M=-1.\frac{1}{2}-y_M.\frac{1}{2}\end{array}\right. \\ \iff \left\{\begin{array}{c}k=\frac{1}{2}\\ 3-y_M=-\frac{1}{2}-\frac{1}{2}{y}_M\end{array}\right. \\ \iff \left\{\begin{array}{c}k=\frac{1}{2}\\ -y_M+\frac{1}{2}{y}_M=-\frac{1}{2}-3\end{array}\right. \\ \iff \left\{\begin{array}{c}k=\frac{1}{2}\\ -\frac{1}{2}{y}_M=-\frac{7}{2}\end{array}\right.\iff \left\{\begin{array}{c}k=\frac{1}{2}\\ y_M=7\end{array}\right. \end{gathered}$$

Vậy giá trị của k là $\frac{1}{2}$ .

Câu 40: Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại 1 điểm trên trục tung ?

Lời giải:

Đồ thị 2 hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại 1 điểm trên trục tung nên ta thay hoành độ x = 0 vào:

Hàm số y = 2x + (3 + m) ta được tung độ: y = 3 + m

Hàm số y = 3x + (5 – m) ta được tung độ: y = 5 – m

Vì cùng là tung độ của giao điểm nên: 3 + m = 5 – m ⇒ m = 1

Vậy khi m = 1 thì 2 đường thẳng đã cho cắt nhau tại 1 điểm trên trục tung.

Câu 41: Chứng minh rằng: Khoảng cách từ 1 điểm trên đường chéo của hình thoi đến các cạnh kề với đường chéo ấy thì tỉ lệ nghịch với các cạnh ấy.

Lời giải:

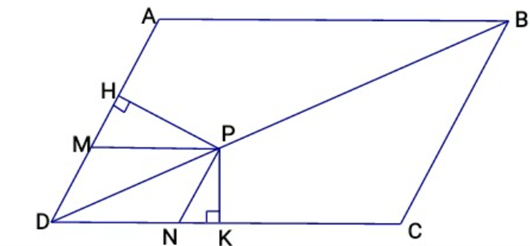
Kẻ PH ⊥ AD; PK ⊥ CD; PM // CD; PN // AD

∆HMP  ∆KNP (g.g)

$\Rightarrow \frac{PH}{PK}=\frac{PM}{PN}\Rightarrow \frac{PH}{PK}=\frac{DN}{PN}$ (Do PMDN là hình bình hành)

∆DNP $\#$ $\Delta DCB$ (g.g) $\Rightarrow \frac{DN}{DC}=\frac{PN}{BC}$

$\Rightarrow \frac{DN}{PN}=\frac{DC}{BC}\Rightarrow \frac{PH}{PK}=\frac{DC}{BC}\Rightarrow PH.BC=PK.DC$

PH.AD = PK.DC (điều phải chứng minh).

Câu 42: Lúc 8h, 1 ô tô đi từ Hà Nội với vận tốc 52 km/h, cùng lúc đó 1 xe thứ 2 đi từ Hải Phòng đến Hà Nội vận tốc 48 km/h. Hà Nội cách Hải Phòng 100 km (coi là đường thẳng). Lập phương trình chuyển động của 2 xe trên cùng 1 hệ trục tọa độ. Lấy Hà Nội làm gốc tọa độ và chiều đi từ Hà Nội đến Hải Phòng là chiều dương, gốc thời gian là lúc 8h.

Lời giải:

Phương trình chuyển động của xe đi từ Hà Nội: $x_1=x_0+v_{1}t=52t$

Phương trình chuyển động của xe đi từ Hải Phòng: $x_2=100-v_{2}t=100-48t$ .

Câu 43: Tìm GTNN của $D=x^4-2x^3+3x^2-2x+1$ .

Lời giải:

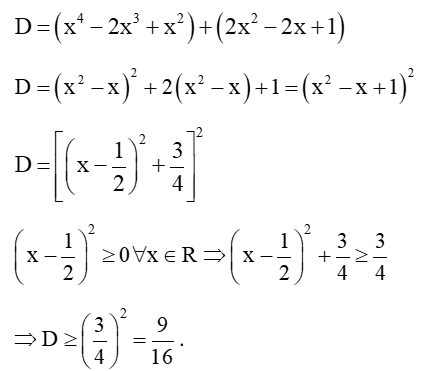
Câu 44: Cho ∆ABC có $\widehat{B}=60°,\widehat{C}=40°,BC=6cm.$ Tính:

a. Đường cao AH và cạnh AC.

b. Tính diện tích ∆ABC.

Lời giải:

a. Ta có: BH + HC = BC

⟺ AH.cotB + AH.cotC = BC

$\iff AH.\left(\frac{\sqrt{3}}{3}+\mathrm{1,3}\right)=BC\iff AH\mathrm{.1,9}=10\Rightarrow AH=\mathrm{5,3}\left(cm\right)$

$\Rightarrow AC=\frac{AH}{\sin C}=\frac{\mathrm{5,3}}{\mathrm{0,6}}=\mathrm{8,2}\left(cm\right)$

b. Ta có: $S_{ABC}=\frac{AH.BC}{2}=\frac{\mathrm{5,3.10}}{2}=\mathrm{26,5}\left(c{m}^2\right)$ .

Câu 45: Tìm tập xác định của hàm số $y=\frac{1-2\cos x}{\sin 3x-\mathrm{s}\text{inx}}$ .

Lời giải:

ĐKXĐ: sin3x – sinx ≠ 0

$\Rightarrow \sin 3x\ne \mathrm{s}\text{inx}\Rightarrow \left[\begin{array}{c}3x\ne x+k2\pi \\ 3x\ne \pi -x+k2\pi \end{array}\right.\Rightarrow \left[\begin{array}{c}x\ne k\pi \\ x\ne \frac{\pi }{4}+\frac{k\pi }{2}\end{array}\right.$.

Câu 46: Tìm x biết: $150-x^5+18=118$ .

Lời giải:

$$\begin{gathered} 150-x^5+18=118\iff x^5=150+18-118 \\ \iff x^5=50\iff x=50:5\iff x=10 \end{gathered}$$

Câu 47: Hai anh em cùng trồng 400 cây trên mảnh vườn của gia đình, nhiệm vụ mỗi anh em phải trông 200 cây. Biết trong 1 ngày, cả 2 anh em trồng được tổng cộng 90 cây và số ngày để người anh trồng xong ít hơn số ngày người em trồng xong 1 ngày. Hỏi mỗi anh em trồng được bao nhiêu cây trong 1 ngày ?

Lời giải:

Gọi x; y cây (x; y > 0) lần lượt là số cây mà anh em mỗi người trồng trong 1 ngày.

Cả 2 người trông 90 cây 1 ngày nên x + y = 90

Thời gian để anh, em trồng xong lần lượt là $\frac{200}{x};\frac{200}{y}$ ngày

Vì anh trồng ít hơn em 1 ngày nên $\frac{200}{y}-\frac{200}{x}=1$

Ta có hệ PT:

$$\begin{gathered} \left\{\begin{array}{c}x+y=90\\ \frac{200}{y}-\frac{200}{x}=1\end{array}\right.\iff \left\{\begin{array}{c}x=90-y\\ \frac{200}{y}-\frac{200}{90-y}=1\end{array}\right. \\ \iff \left\{\begin{array}{c}x=90-y\\ 200(90-y)-200y=y(90-y)\end{array}\right. \\ \iff \left\{\begin{array}{c}x=90-y\\ 18000-400y=90y-y^2\end{array}\right. \\ \iff \left\{\begin{array}{c}x=90-y\\ y^2-490y+18000=0\end{array}\right. \\ \iff \left\{\begin{array}{c}x=90-y\\ y=40;y=450\end{array}\right. \end{gathered}$$

$\iff \left\{\begin{array}{c}x=50\\ y=40\end{array}\right.$ (nhận) hoặc $\left\{\begin{array}{c}x=-360\\ y=450\end{array}\right.$ (loại)

Vậy 1 ngày anh trồng 50 cây, em trồng 40 cây.

Câu 48: Làm tròn đến số thập phân thứ nhất: 0,2288.

Lời giải:

0,2288 xấp xỉ 0,2 (làm tròn đến chữ số thập phân thứ nhất)

Giải thích: Sau số 2 là 1 số nhỏ hơn 5 thì giữ nguyên ⇒ Kết quả 0,2.

Câu 49: Tìm số $\overline{abc}$ . Biết $\overline{abc}$ chia hết cho 45 và $\overline{abc}-\overline{cba}=396$  (với c ≠ 0).

Lời giải:

$\overline{abc}$ chia hết cho 45 nên $\overline{abc}$  chia hết cho 5 và 9 nên c = 0 hoặc 5 mà c ≠ 0 nên c = 5

Ta có: $\overline{ab5}-\overline{5ba}=396$

Ta viết lại biểu thức như sau: $396+\overline{5ba}=\overline{ab5}$

6 + a tận cùng là 5 nên a = 9

Nên ta lại có: $\overline{abc}=\overline{9b5}$  chia hết cho 9 và 5

Nên 9 + b + 5 chia hết cho 9, nên b = 4

Suy ra  $\overline{abc}$= 945

Câu 50: Cộng, trừ phân thức: $\frac{1}{2x+2}-\frac{x-1}{3x^2+6x+3}$ .

Lời giải:

ĐKXĐ: x ≠ –1

$$\begin{gathered} \frac{1}{2x+2}-\frac{x-1}{3x^2+6x+3}=\frac{1}{2(x+1)}-\frac{x-1}{3(x^2+2x+1)} \\ =\frac{1}{2(x+1)}-\frac{x-1}{3{(x+1)}^2}=\frac{3(x+1)}{2(x+1).3(x+1)}-\frac{2(x-1)}{3{(x+1)}^2.2} \\ =\frac{3x+3}{6{(x+1)}^2}-\frac{2x-2}{6{(x+1)}^2}=\frac{3x+3-2x+2}{6{(x+1)}^2}=\frac{x+5}{6{(x+1)}^2} \end{gathered}$$

Câu 51: Tìm x biết: 2x(3x + 5) – x(6x – 1) = 33.

Lời giải:

2x(3x + 5) – x(6x – 1) = 33

$$\begin{gathered} \iff 6x^2+10x-6x^2+1=33 \\ \iff 10x+1=33\iff 10x=32 \\ \iff x=\mathrm{3,2} \end{gathered}$$

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 19)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 20)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 21)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 22)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 23)