1500 câu hỏi ôn tập môn Toán có đáp án (Phần 83)

1500 câu hỏi ôn tập Toán (Phần 83)

Câu 1: Một cửa hàng có 7 gian chứa muối. Mỗi gian có 85 bao muối. Mỗi bao muối nặng 5 yến. Hỏi cửa hàng có tất cả bao nhiêu kg muối ? (giải bằng hai cách).

Lời giải:

Cách 1:

Số bao muối của 7 gian muối là:

85 × 7 = 595 (bao muối)

Khối lượng muối cửa hàng có tất cả là:

595 × 5 = 2 975 (yến muối)

Đổi 2 975 yến = 29 750 kg

Cách 2:

Số yến  muối của mỗi gian muối là:

7 × 5 = 35 (yến)

Đổi 35 yến = 350 kg

Khối lượng muối của hàng tất cả là:

350 × 85 = 29 750 (kg muối)

Vậy cửa hàng có 29 750 kg muối.

Câu 2: Một người đổ thêm 50 gam muối vào một bình chứa 350 gam nước muối loại 10 % muối. Hỏi người đó nhận được một bình nước chứa bao nhiêu phần trăm muối?

Lời giải:

Khối lượng muối trong 350 g nước muối loại 10% là:

350 : 100 × 10 = 35 (g)

Khối lượng muối sau khi thêm vào là :

50 + 35 = 85 (g)

Tỉ lệ phần trăm muối cần tìm là :

85 × 100 : (350 + 50) = 21,25%

Vậy khi đó bình nước chứa 21, 25% muối.

Câu 3: Có một tuần trung bình nhà máy A mỗi ngày tiêu thụ hết 1 165 250 lít nước, nhà máy B mỗi ngày tiêu thụ hết 8 071 750 lít nước. Hỏi trong cả tuấn đó, hai nhà máy tiêu thụ bao nhiêu lít nước?

Lời giải:

Trong 1 tuần nhà máy A tiêu thụ hết:

1 165 250 × 7 = 8 156 750 (lít nước)

Trong 1 tuần nhà máy B tiêu thụ hết:

8 071 750 × 7 = 56 502 250 (lít nước)

Trong cả tuần đó, hai nhà máy tiêu thụ hết:

8 156 750 + 56 502 250 = 64 659 000 (lít nước)

Vậy trong cả tuần đó, hai nhà máy tiêu thụ hết 64 659 000 lít nước.

Câu 4: Tính:

a) (10 – 9,34) + (10 – 9,66);

b) 12 – (12 – 9,36).

Lời giải:

a) (10 – 9,34) + (10 – 9,66)

= 10 – 9,34 + 10 – 9,66

= (10 + 10) + (–9,34 – 9,66)

= 20 – 19

= 1.

b) 12 – (12 – 9,36)

= 12 – 12 + 9,36

= 0 + 9,36

= 9,36.

Câu 5: Tìm số nguyên x, y thỏa mãn (x + 3)²⁰²² + (y – 2)²⁰²² = 0.

Lời giải:

Vì (x + 3)²⁰²² ≥ 0 với mọi x

(y – 2)²⁰²² ≥ 0 với mọi y

Nên (x + 3)²⁰²² + (y – 2)²⁰²² ≥ 0 với mọi x, y

Dấu “ = ” xảy ra khi

$\left\{\begin{array}{l}x+3=0\\ y-2=0\end{array}\right.\iff \left\{\begin{array}{l}x=-3\\ y=2\end{array}\right.$

Vậy x = –3, y = 2 là nghiệm của phương trình đã cho.

Câu 6: Cho x là tổng của tất cả các số nguyên tố có 2 chữ số, y là số nguyên âm lớn nhất. Hãy tính giá trị của biểu thức A = 2009 . x²⁰⁰⁶ – 2008 . y²⁰⁰⁷.   

Lời giải:

Vì x là tổng các số nguyên có 2 chữ số

Nên x = 0

Vì y số nguyên âm lớn nhất

Nên y = –1

Thay x = 0, y = –1 vào A ta có:

A = 2009 . 0²⁰⁰⁶ – 2008 . (–1)²⁰⁰⁷

A = 2009 . 0 – 2008 . (–1) 

A = 0 + 2008

A = 2008.

Câu 7: Cho dãy số sau: 16, 06, 68, 88, ?, 98. Hãy tìm số thích hợp thay cho dấu “ ?”.

Lời giải:

Ta thấy

98 quay ngược được 86

88 quay ngược được 88

68 quay ngược được 898

06 quay ngược được 90

16 quay ngược được 91

Suy ra số nằm giữa 86 và 88 là 87 

Vậy số cần tìm là 87.

Câu 8: Hai đội công nhân cùng đào một con đường dài 900 m, đội thứ nhất đào ít hơn đội thứ hai 164 m. Hỏi mỗi đội đào được bao nhiêu mét đường?

Lời giải:

Ta thấy nếu đội thứ hai bớt đi 164 m thì bằng đội thứ nhất, vậy tổng trừ đi hiệu thì được 2 lần đội thứ nhất.

Đội thứ nhất đào được số mét đường là:

(900 – 164) : 2 = 368 (m)

Đội thứ hai đào được số mét đường là:

900 – 368 = 532 (m)

Vậy đội thứ nhất đào được 368 m, đội thứ hai đào được 532 m.

Câu 9: Tính hợp lý: (10² + 11² + 12²) : (13² + 14²).

Lời giải:

Ta có:

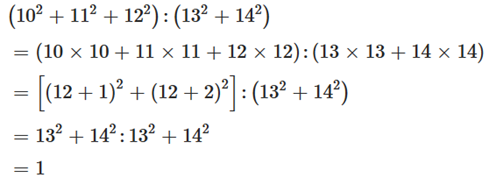
Vậy (10² + 11² + 12²) : (13² + 14²) = 1.

Câu 10: Cho a + b + c + d = 0. Chứng minh rằng a³ + b³ + c³ + d³ = 3(c + d)(ab – cd).

Lời giải:

Ta có a + b + c + d = 0

⇔ a + b = – c – d

⇔ (a + b)³ = (– c – d)³

⇔ a³ + b³ + 3ab(a + b) = – c³ – d³ – 3cd(c + d)

⇔ a³ + b³ + c³ + d³ = – 3cd(c + d) – 3ab(a + b)

⇔ a³ + b³ + c³ + d³ = – 3cd(c + d) + 3ab(c + d)

⇔ a³ + b³ + c³ + d³ = 3(c + d)(ab – cd)

Vậy a³ + b³ + c³ + d³ = 3(c + d)(ab – cd).

Câu 11: Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?

A. 1470;

B. 750;

C. 2940;

D. 1500.

Lời giải:

Đáp án đúng là: D

Sắp xếp cụm số 3, 4, 5 có 2 cách sắp xếp là 345 và 543

TH1: Cụm 2 số 3, 4, 5 đứng đầu có:

2 . 7 . 6 . 5 = 240 số thỏa mãn

TH2: Cụm 3 số 3, 4, 5 không đứng đầu có 3 cách sắp xếp là $\overline{a345bc},\overline{ab345c},\overline{abc345}$

3 chữ số còn lại có: 6 . 6 . 5 = 180 cách chọn và sắp xếp

Do đó có 2 . 3 . 180 = 1 080 số thỏa mãn

Theo quy tắc cộng có:

420 + 1 080 = 1 500 số thỏa mãn yêu cầu bài toán

Vậy ta chọn đáp án D.

Câu 12: Hai thùng chứa 100 lít dầu. Sau khi đổ 10 lít từ thùng 1 sang thùng thứ 2 thì số dầu thùng thứ 2 bằng $\frac{2}{3}$ số ở thùng 1. Hỏi ban đầu mỗi thùng có bao nhiêu lít dầu?

Lời giải:

Sau khi đổ 10 lít từ thùng 1 sang thùng 2 thì tổng số lít dầu không thay đổi (vẫn là 100 lít)

Số lít dầu của thùng 1 sau khi chuyển là:

100 : (2 + 3) × 3 = 60 (l)

Số lít dầu của thùng 2 sau khi chuyển là:

100 : (2 + 3) × 2 = 40 (l)

Số lít dầu của thùng 1 ban đầu là:

60 + 10 = 70 (l)

Số lít dầu của thùng 2 ban đầu là:

40 – 10 = 30 (l)

Vậy ban đầu thùng 1 có 70 lít dầu và thùng 2 có 30 lít dầu.

Câu 13: Mỗi giờ xe ô tô chạy nhanh hơn xe đạp 46 km. Biết rằng xe ô tô chạy nhanh gấp 5 lần xe đạp. Hỏi mỗi xe chạy được bao nhiêu km trong 1 giờ?

Lời giải:

Mỗi giờ xe đạp chạy được số km là 

46 : (5 – 1) = 11,5 (km)

Mỗi giờ xe ô tô chạy được số km là 

11,5 × 5 = 57,5 (km)

Vậy mỗi giờ ô tô chạy được 57,5 km và xe đạp chạy được 11,5 km.

Câu 14: Tìm số hữu tỉ a sao cho x³ + ax² + 5x + 3 chia hết cho x² + 2x + 3.

Lời giải:

Đặt f(x) = x³ + ax² + 5x + 3 và g(x) = x² + 2x + 3

h(x) là thương của phép chia f(x) cho g(x)

Ta có f(x) bậc 3, g(x) bậc 2 nên h(x) bậc 1

Suy ra h(x) có dạng x + b

Vì f(x) ⋮ g(x) nên f(x) = g(x) . h(x)

⇔ x³ + ax² + 5x + 3 = (x² + 2x + 3)(x + b)

⇔ x³ + ax² + 5x + 3 = x³ + bx² + 2x² + 2xb + 3x + 3b

⇔ x³ + ax² + 5x + 3 = x³ + x²(b + 2) + x(2b + 3) + 3b

$\iff \left\{\begin{array}{l}a=b+2\\ 5=2b+3\\ 3=3b\end{array}\right.\iff \left\{\begin{array}{l}b=1\\ a=3\end{array}\right.$

Vậy a = 3.

Câu 15: Một phân xưởng có 24 máy dệt, mỗi ngày dệt được 264 áo. Nếu phân xưởng đó có thêm 12 máy nữa thì mỗi ngày dệt được tất cả bao nhiêu áo? (Năng suất mỗi máy không đổi).

Lời giải:

Nếu thêm 12 máy nữa thì phân xưởng có: 

24 + 12 = 36 (máy)

Mỗi máy dệt được số áo mỗi ngày là:

264 : 24 = 11 (cái áo)

Mỗi ngày 36 máy dệt được là:

36 × 11 = 396 (cái áo)

Vậy thêm 12 máy nữa thì mỗi ngày dệt được 396 cái áo.

Câu 16: Phân tích đa thức thành nhân tử: x² – 49 + y² – 2xy.

Lời giải:

Ta có:

x² – 49 + y² – 2xy

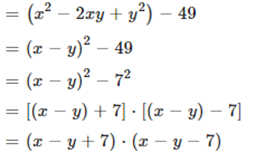
Câu 17: Viết kết quả viết dưới dạng lũy thừa:

a) 125 : 5²;

b) 27⁵ : 81³;

c) 8⁴ × 16⁵ × 32;

d) 27⁴ × 81¹⁰ .

Lời giải:

a) 125 : 5² = 5³ : 5² = 5^3-2 = 5.

b) 27⁵ : 81³ = (3³)⁵ : (3⁴)³ = 3¹⁵ : 3¹² = 3^15-12 = 3³.

c) 8⁴ × 16⁵ × 32 = (2³)⁴ × (2⁴)⁵ × 2⁵ = 2¹² × 2²⁰ × 2⁵ = 2^12+20+5 = 2³⁷.

d) 27⁴ × 81¹⁰ = (3³)⁴ × (3⁴)¹⁰ = 3¹² × 3⁴⁰ = 3¹²⁺⁴⁰ = 3⁵².

Câu 18: Tính nhanh:

a) 34² + 66² + 68 . 66;

b) 74² + 24² – 48 . 74.

Lời giải:

a) 34² + 66² + 68 . 66

= 34² + 2 . 34 . 66 + 66²

= (34 + 66)²

= 100²

= 10 000.

b) 74² + 24² – 48 . 74

= 74² – 2 . 74 . 24 + 24²

= (74 – 24)²

= 50²

= 2 500.

Câu 19: Cửa hàng bán số gạo tẻ nhiều hơn số gạo nếp 36 kg, trong đó số gạo nếp bằng $\frac{3}{5}$ số gạo tẻ. Hỏi mỗi loại bán được bao nhiêu kg?

Lời giải:

Số kg gạo nếp bán được là:

36 : (5 – 3) × 3 = 54 (kg)

Số kg gạo tẻ bán được là:

54 + 36 = 90 (kg)

Vậy cửa hàng bán được 54 kg gạo nếp và 90 kg gạo tẻ.

Câu 20: Hai bác thợ cưa một cây gỗ dài 7 m thành những đoạn dài 1 m. Cứ 12 phút thì cưa xong một đoạn. Hỏi cưa cả cây gỗ đó hết bao lâu?

Lời giải:

Cưa cây gỗ dài 7 m được số đoạn là:

7 : 1 = 7 (đoạn)

Cưa cả cây gỗ đó hết:

7 × 12 = 84 (phút)

Vậy cưa cả cây gỗ hết 84 phút.

Câu 21: May 3 bộ quần áo hết 7 m vải. Hỏi may 9 bộ quần áo như thế hết bao nhiêu mét vải?

Lời giải:

9 bộ gấp 3 bộ số lần là:

9 : 3 = 3 (lần)

May 9 bộ quần áo cần số mét vải là:

7 × 3 = 21 (m)

Vậy may 9 bộ quần áo hết 21 m vải.

Câu 22: Một đội công nhân 9 người trong một ngày đắp được 60 mét đường. Người ta bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được bao nhiêu mét đường đó (mức đắp mỗi người như nhau)?

Lời giải:

Số người công nhân hiện có là:

9 + 18 = 27 (người)

27 người đắp được số m đường là:

27 : 9 × 60 = 180 (m)

Vậy bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được 180 mét đường.

Câu 23: Mẹ có 1 số tiền nếu mua táo với giá 8 000 đồng 1 kg thì mẹ mua được 3 kg. Hỏi nếu mua mận với giá 6 000 một kg thì mẹ mua được bao nhiêu kg mận ?

Lời giải:

Số tiền mẹ có là: 8 000 × 3 = 24 000 (đồng)

Số ki – lô – gam mận mẹ mua được là:

24 000 : 6 000 = 4 (kg)

Vậy mẹ mua được 4 kg mận.

Câu 24: Một bếp ăn tập thể dự trữ gạo đủ cho 85 người ăn trong 18 ngày. Sau đó vì có thêm người đến ăn nên số gạo chỉ đủ ăn trong 15 ngày. Hỏi có bao nhiêu người đến ăn thêm (mức ăn mỗi người bằng nhau).

Lời giải:

1 ngày có số người ăn hết từng đó số gạo là:

85 × 18 = 1 530 (người)

Trong 15 ngày thì có số người ăn hết là:

1 530 : 15 = 102 (người)

Số người đến ăn thêm là:

102 – 85 = 17 (người)

Vậy có 17 người đến ăn thêm.

Câu 25: Một máy in cần 5 giây để in 1 trang giấy và cứ sau 1 giờ in liên tục thì cần 4 phút để máy in nghỉ. Hỏi mất bao nhiêu phút để máy in sẽ in hết 3 600 trang giấy.

Lời giải:

Số giây để in hết 3 600 trang giấy là:

3 600 × 5 = 18 000 (giây)

Đổi 18 000 giây = 300 phút = 5 giờ 

Số phút để máy nghỉ là:

4 × 5 = 20 (phút)

Thời gian để in hết 3 600 trang giấy là:

300 + 20 = 320 (phút)

Vậy cần 320 phút để in hêt 3 600 trang giấy.

Câu 26: Một đơn vị bộ đội dự trữ gạo đủ cho 150 người ăn trong 20 ngày. Nhưng sau đó lại có thêm một số bộ đội chuyển đến nên số ngày ăn hết số gạo dự trữ giảm đi 8 ngày. Hỏi có bao nhiêu bộ đội mới chuyển đến?

Lời giải:

Coi số gạo mỗi người ăn một ngày là một suất gạo.

Đơn vị bộ đội đó chuẩn bị số suất gạo là: 150 × 20 = 3000 (suất).

Thực tế đơn vị đã ăn trong tổng số ngày là: 20 – 8 = 12 (ngày).

Tổng số bộ đội là: 3000 : 12 = 250 (người).

Số người đã chuyển đến là: 250 – 150 = 100 (người).

Đáp số: 100 người.

Câu 27: Mùng 1 tháng 1 năm 2015 là thứ 5. Hỏi ngày mùng 1 tháng 1 năm 2016 là thứ mấy?

Lời giải:

Vì 2015 không chia hết cho 4 nên năm 2015 là năm có 365 ngày.

1 tuần có 7 ngày.

365 : 7 = 52 dư 1.

Suy ra 1 năm có 52 tuần và dư 1 ngày.

Do đó nếu mùng 1 tháng 1 năm 2015 là thứ năm thì ngày 31 tháng 12 năm 2015 cũng là thứ 5.

Vậy mùng 1 tháng 1 năm 2016 là thứ 6.

Câu 28: Số bị chia hơn số chia 60 đơn vị. Nếu giảm số chia đi một nửa thì thương mới là 32. Tìm số bị chia và số chia lúc đầu.

Lời giải:

Nếu giảm số chia đi một nửa thì thương tăng lên 2 lần, do đó thương lúc đầu là:

32 : 2 = 16.

Coi số bị chia là 16 phần thì số chia là 1 phần như thế.

Hiệu số phần bằng nhau là: 16 – 1 = 15 (phần).

Số bị chia là: 60 : 15 × 16 = 64.

Số chia là: 60 : 15 × 1 = 4.

Đáp số: Số bị chia: 64;

             Số chia: 4.

Câu 29: Tính nhanh: 413 – (113 + 523) + 823.

Lời giải:

Ta có 413 – (113 + 523) + 823

= (413 – 113) – 523 + 823

= 300 + 300

= 600.

Câu 30: Đội văn nghệ của một trường có 48 nam và 72 nữ về một huyện để biểu diễn. Muốn phục vụ đồng thời tại nhiều địa điểm, đội dự định chia thành các tổ gồm cả nam và nữ, số nam được chia đều vào các tổ, số nữ cũng vậy.

Có thể chia được nhiều nhất thành bao nhiêu tổ?

Khi đó mỗi tổ có bao nhiêu nam, bao nhiêu nữ?

Lời giải:

Giả sử đội văn nghệ chia được nhiều nhất là k tổ (k ∈ ℕ*).

Vì số nam được chia đều vào các tổ nên 48 ⋮ k hay k ∈ Ư(48)   (1)

Vì số nữ được chia đều vào các tổ nên 72 ⋮ k hay k ∈ Ư(72)    (2)

Từ (1), (2), suy ra k ∈ ƯC(48, 72).

Mà k là số lớn nhất nên k = ƯCLN(48, 72).

Ta có 48 = 2⁴.3 và 2³.3².

Suy ra ƯCLN(48, 72) = 2³.3 = 24.

Do đó k = 24.

Vậy có thể chia được nhiều nhất thành 24 tổ.

Khi đó mỗi tổ có 48 : 24 = 2 (nam) và 72 : 24 = 3 (nữ).

Câu 31: Tìm ước chung của 16 và 30.

Lời giải:

Ta có 16 = 2⁴ và 30 = 2.3.5.

Lập tích các thừa số chung, mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2.

Suy ra ƯCLN(16, 30) = 2.

Vậy ƯC(16, 30) = {1; 2}.

Câu 32: Hiện nay tổng số tuổi của bố, mẹ và con là 66. Sau 10 năm nữa thì tổng số tuổi của hai mẹ con hơn tuổi của bố là 8 và tuổi mẹ bằng ba lần tuổi con. Tính số tuổi của mỗi người hiện nay.

A. Tuổi con: 2; Tuổi mẹ: 29; Tuổi bố 35.

B. Tuổi con: 3; Tuổi mẹ: 29; Tuổi bố 34.

C. Tuổi con: 4; Tuổi mẹ: 28; Tuổi bố 34.

D. Tuổi con: 2; Tuổi mẹ: 28; Tuổi bố 36.

Lời giải:

Tổng số tuổi của ba người sau 10 năm nữa là: 66 + 10 . 3 = 96 (tuổi).

Tuổi của bố sau 10 năm nữa là: (96 – 8) : 2 = 44 (tuổi).

Tuổi của bố hiện nay là: 44 – 10 = 34 (tuổi).

Tổng số tuổi của hai mẹ con sau 10 năm nữa là: 96 – 44 = 52 (tuổi).

Tuổi của con sau 10 năm nữa là: 52 : (3 + 1) . 1 = 13 (tuổi).

Tuổi của con hiện nay là: 13 – 10 = 3 (tuổi).

Tuổi của mẹ hiện nay là: 66 – 34 – 3 = 29 (tuổi).

Vậy hiện nay bố 34 tuổi; mẹ 29 tuổi và con 3 tuổi.

Do đó ta chọn phương án B.

Câu 33: Tìm các bội chung của 15 và 25 mà nhỏ hơn 400.

Lời giải:

Ta có 15 = 3.5 và 25 = 5².

Suy ra BCNN(15, 25) = 3.5² = 75.

Do đó BC(15, 25) = B(75) = {0; 75; 150; 225; 300; 375; 450; 525; ...}.

Vậy các bội chung của 15 và 25 mà nhỏ hơn 400 là: {0; 75; 150; 225; 300; 375}.

Câu 34: Cho tam giác ABC cân tại A, đường cao CD. Chứng minh rằng:

AB² + BC² + AC² = BD² + 2AD² + 3CD².

Lời giải:

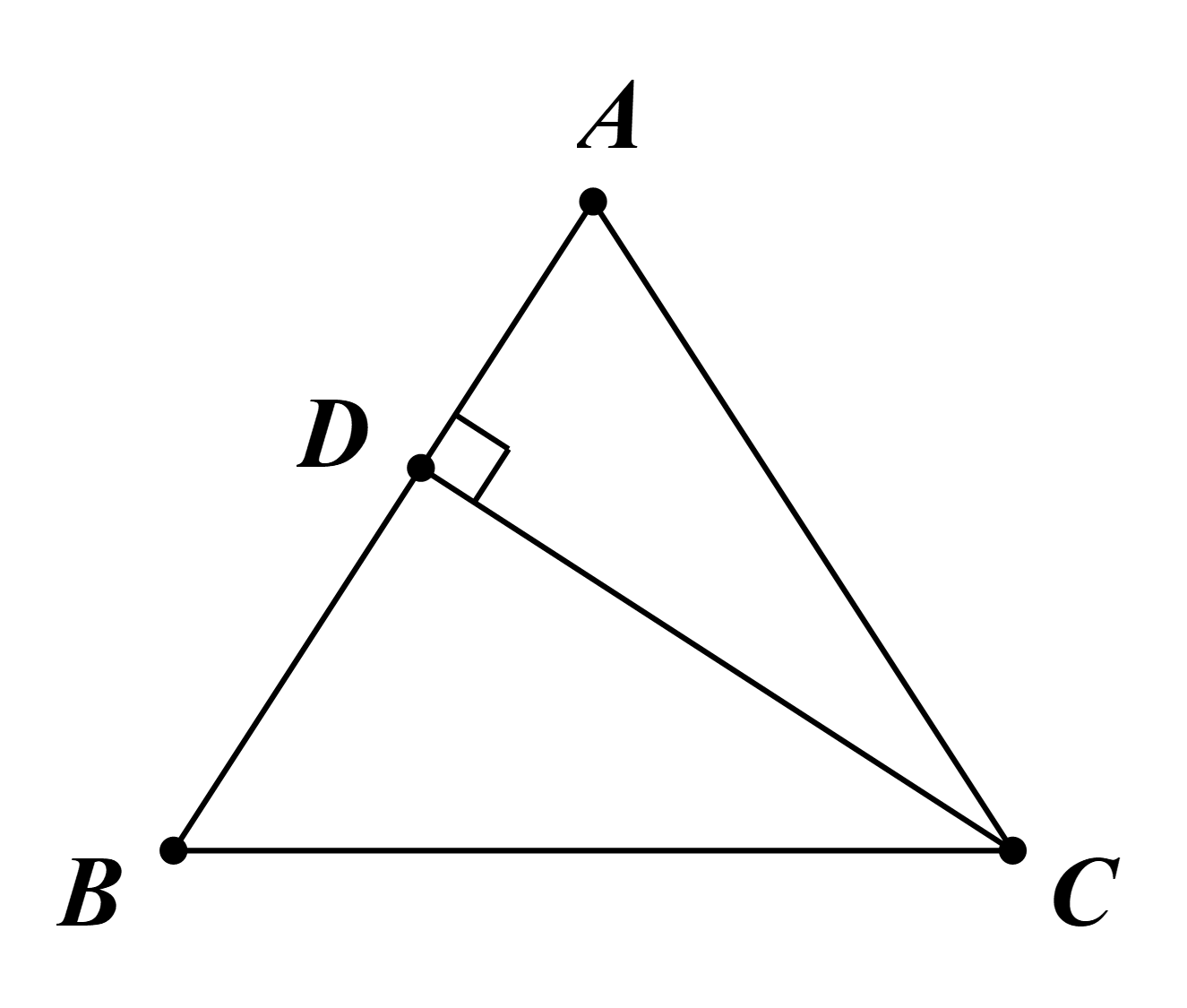
Áp dụng định lí Pytago cho tam giác ACD vuông tại D: AD² + CD² = AC²   (1)

⇔ AD² + CD² = AB² (do tam giác ABC cân tại A nên AB = AC)    (2)

Áp dụng định lí Pytago cho tam giác DBC vuông tại D: BD² + CD² = BC²    (3)

Lấy (1) + (2) + (3) vế theo vế, ta được: BD² + 2AD² + 3CD² = AB² + BC² + AC².

Vậy ta có điều phải chứng minh.

Câu 35: Đổi ra số thập phân: 1300 kg = ... tấn.

Lời giải:

Xác định các đơn vị nằm giữa tấn và kg là: tấn, tạ, yến, kg.

Ta có bảng sau:

Đề bài yêu cầu đổi sang đơn vị là tấn nên ta đặt dấu phẩy sau số 1.

Vậy 1300 kg = 1,3 tấn.

Câu 36: Một thửa ruộng hình chữ nhật có chu vi 0,18 km, chiều rộng bằng $\frac{4}{5}$  chiều dài.

a) Tính diện tích thửa ruộng với đơn vị là m², ha.

b) Người ta cấy lúa trên thửa ruộng đó, cứ 100 m² thu được 65 kg thóc. Hỏi cả thửa ruộng người ta thu được bao nhiêu tấn thóc?

Lời giải:

a) Nửa chu vi của thửa ruộng là:

      0,18 : 2 = 0,09 (km).

Chiều rộng của thửa ruộng là:

      0,09 : (4 + 5) × 4 = 0,04 (km).

Chiều dài của thửa ruộng là:

      0,09 : (4 + 5) × 5 = 0,05 (km).

Diện tích của thửa ruộng là:

      0,05 × 0,04 = 0,002 (km²).

Đổi: 0,002 km² = 0,2 ha = 2000 m².

b) Số kg thóc người ta thu hoạch được trên cả thửa ruộng là:

      2000 × 65 : 100 = 1300 (kg thóc).

Đổi: 1300 kg = 1,3 tấn.

Đáp số: a) 0,2 ha; 2000 m²;

             b) 1,3 tấn thóc.

Câu 37: Nếu tăng chiều rộng của một hình chữ nhật thêm 27 090 cm và giữ nguyên chiều dài thì diện tích của nó tăng lên 130 lần. Hỏi chiều dài của hình chữ nhật ban đầu là bao nhiêu mét biết chu vi của nó là 850 cm.

Lời giải:

Nửa chu vi của hình chữ nhật ban đầu là: 850 : 2 = 425 (cm).

Gọi chiều dài của hình chữ nhật ban đầu là a (cm).

Suy ra chiều rộng của hình chữ nhật ban đầu là 425 – a (cm).

Nếu tăng chiều rộng của một hình chữ nhật thêm 27090 cm và giữ nguyên chiều dài thì diện tích của nó tăng lên 130 lần.

Suy ra a × (425 – a + 27 090) = 130 × a × (425 – a).

⇒ 27 515 – a = 130 × (425 – a).

⇒ 27 515 – a = 55 250 – 130 × a.

⇒ 130 × a – a = 55 250 – 27515.

⇒ 129 × a = 27 735.

⇒ a = 27 735 : 129 = 215 (cm).

Đổi: 215 cm = 2,15 m.

Đáp số: 2,15 m.

Câu 38: Phân tích đa thức thành nhân tử: (xy – 1)² + (x + y)².

Lời giải:

Ta có (xy – 1)² + (x + y)²

= x²y² – 2xy + 1 + x² + 2xy + y²

= (x²y² + y²) + (x² + 1)

= y²(x² + 1) + (x² + 1)

= (x² + 1)(y² + 1).

Câu 39: Chuyển thành tỉ số phần trăm: 9,03.

Lời giải:

Ta có 9,03 = 903%.

Câu 40: Chứng minh rằng trong 9 người bất kì luôn tìm được 3 người đôi một quen nhau hoặc 4 người đôi một không quen nhau.

Lời giải:

Xét người A bất kì trong 9 người.

Khi đó A quen hoặc không quen với mỗi người trong 8 người còn lại.

Do đó theo nguyên lí Dirichlet, tồn tại ít nhất $1+\left[\frac{8-1}{2}\right]=4$  người quen hoặc không quen A.

Vậy trong 9 người bất kì luôn tìm được 3 người đôi một quen nhau hoặc 4 người đôi một không quen nhau.

Câu 41: Cho A = 2 + 2² + 2³ + ... + 2²⁰. Chứng minh rằng:

a) A chia hết cho 2.

b) A chia hết cho 3.

c) A chia hết cho 5.

Lời giải:

a) Ta có A = 2 + 2² + 2³ + ... + 2²⁰.

= 2.(1 + 2 + 2² + ... + 2¹⁹).

Vì 2 ⋮ 2 nên 2.(1 + 2 + 2² + ... + 2¹⁹) ⋮ 2.

Vậy A ⋮ 2.

b) Ta ghép các số hạng của A thành 5 nhóm, mỗi nhóm có 4 số hạng, ta được:

A = 2 + 2² + 2³ + ... + 2²⁰.

= (2 + 2² + 2³ + 2⁴) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)

= 2.(1 + 2 + 2² + 2³) + ... + 2¹⁷.(1 + 2 + 2² + 2³)

= (1 + 2 + 2² + 2³)(2 + 2⁵ + 2⁹ + 2¹³ + 2¹⁷)

= (1 + 2 + 4 + 8)(2 + 2⁵ + 2⁹ + 2¹³ + 2¹⁷)

= 15.(2 + 2⁵ + 2⁹ + 2¹³ + 2¹⁷)

Vì 15 ⋮ 3 nên 15.(2 + 2⁵ + 2⁹ + 2¹³ + 2¹⁷) ⋮ 3.

Vậy A ⋮ 3.

c) Vì 15 ⋮ 5 nên 15.(2 + 2⁵ + 2⁹ + 2¹³ + 2¹⁷) ⋮ 5.

Vậy A ⋮ 5.

Câu 42: Lớp 5A và lớp 5B mua tất cả 86 quyển sách. Nếu lớp 5A chuyển cho lớp 5B 7 quyển và lớp 5B trả lại cho lớp 5A 1 quyển thì hai lớp có số sách bằng nhau. Hỏi lúc đầu mỗi lớp mua bao nhiêu quyển sách?

Lời giải:

Nếu lớp 5A chuyển cho lớp 5B 7 quyển và lớp 5B trả lại cho lớp 5A 1 quyển thì số quyển sách lớp 5A chuyển cho lớp 5B là: 7 – 1 = 6 (quyển).

Khi đó lớp 5A có số quyển sách là: 86 : 2 = 43 (quyển).

Số quyển sách lúc đầu lớp 5A mua là: 43 + 6 = 49 (quyển).

Số quyển sách lúc đầu lớp 5B mua là: 86 – 49 = 37 (quyển).

Đáp số: Lớp 5A: 49 quyển;

             Lớp 5B: 37 quyển.

Câu 43: Các học sinh của một lớp học gồm 45 nam và 35 nữ được xếp ra thành một hàng ngang. Chứng minh rằng trong hàng đó luôn tìm được hai học sinh nam mà ở giữa họ có 8 người đứng xen vào.

Lời giải:

Lớp học đó có tất cả 45 + 35 = 80 học sinh.

Đánh số thứ tự các học sinh từ 1 đến 80.

Xét các học sinh có thứ tự là i và i + 9, với 1 ≤ i ≤ 71.

Ta thấy giữa hai học sinh này luôn có đúng 8 học sinh khác.

– Xét 18 học sinh đầu có số thứ tự từ 1 đến 9 và 10 đến 18; 18 học sinh này chia làm 9 cặp.

– Xét 54 học sinh tiếp theo chia làm 3 nhóm, mỗi nhóm 18 học sinh, mỗi nhóm 18 học sinh này chia làm 9 cặp.

– Khi đó 72 học sinh đầu tiên chia làm 9 + 3.9 = 36 cặp, vậy 8 học sinh cuối ghép thành 8 cặp.

Lúc này ta có các cặp học sinh được đánh số thứ tự như sau:

⦁ (1; 10), (2; 11), ..., (9; 18).

⦁ (19; 28), (20; 29), ..., (27; 36).

⦁ (37; 46), (38; 47), ..., (45; 54).

⦁ (55; 64), (56; 65), ..., (63; 72).

⦁ (64; 73), (65; 74), ..., (71; 80).

Ta thấy có 44 cặp, mỗi cặp 2 học sinh.

Mà lớp học có 45 học sinh nam nên tồn tại ít nhất hai học sinh nam mà ở giữa họ có 8 người đứng xen vào.

Vậy ta có điều phải chứng minh.

Câu 44: Có bao nhiêu số tự nhiên có bốn chữ số lớn hơn 3254.

Lời giải:

Số tự nhiên bé nhất có bốn chữ số lớn hơn 3254 là 3255.

Các số tự nhiên có bốn chữ số lớn hơn 3254 là các số thuộc dãy số: 3255; 3256; 3257; ...; 9999.

Dãy số trên có số số hạng là: (9999 – 3255) : 1 + 1 = 6745 (số hạng).

Đáp số: 6745 số.

Câu 45: Tìm một số thập phân có 3 chữ số ở phần thập phân, biết rằng nếu viết thêm chữ số 2 vào bên phải số đó ta sẽ được một số thập phân khác có giá trị bằng 1,0125 lần số phải tìm.

Lời giải:

Chữ số 2 được viết thêm vào có giá trị bằng 0,0002.

Số phải tìm là: 0,0002 : (1,0125 – 1) = 0,016.

Đáp số: 0,016.

Câu 46: Khối lớp Năm của một trường tiểu học có 150 học sinh, trong đó có 52% là học sinh gái. Hỏi khối lớp Năm của trường đó có bao nhiêu học sinh trai?

Lời giải:

Tỉ số phần trăm số học sinh trai và tổng số học sinh của khối lớp 5 là:

100% – 52% = 48%.

Số học sinh trai của khối lớp 5 là:

150 × 48 : 100 = 72 (học sinh).

Đáp số: 72 học sinh.

Câu 47: Một hình chữ nhật có chiều rộng 16,34 m, chiều dài hơn chiều rộng 8,32 m. Tính chu vi hình chữ nhật đó.

Lời giải:

Chiều dài hình chữ nhật đó là: 16,34 + 8,32 = 24,66 (m).

Chu vi hình chữ nhật đó là: (24,66 + 16,34) × 2 = 82 (m).

Đáp số: 82 m.

Câu 48: Ngày 9 tháng 5 năm 2010 là ngày chủ nhật. Vậy ngày 18 tháng 6 năm 2010 là thứ mấy?

Lời giải:

Từ ngày 9 tháng 5 năm 2010 đến ngày 9 tháng 6 năm 2010 có 32 ngày.

Từ ngày 10 tháng 6 năm 2010 đến ngày 18 tháng 6 năm 2010 có 9 ngày.

Suy ra từ ngày 9 tháng 5 năm 2010 đến ngày 18 tháng 6 năm 2010 có 41 ngày.

Mà 41 : 7 = 5 dư 6.

Ta có bảng sau:

Vậy ngày 18 tháng 6 năm 2010 là thứ 6.

Câu 49: Số bé nhất có sáu chữ số mà chữ số hàng trăm là 8 và chữ số hàng đơn vị là 3 là:

A. 100 813;

B. 111 813;

C. 100 803;

D. 999 893.

Lời giải:

Số bé nhất có sáu chữ số trong đó chữ số hàng trăm là 8 và chữ số hàng đơn vị là 3 thì:

+ Chữ số hàng cao nhất là chữ số bé nhất khác 0 nên chữ số hàng trăm nghìn là 1.

+ Chữ số hàng chục nghìn là chữ số bé nhất nên chữ số hàng chục nghìn là 0.

+ Chữ số hàng nghìn là chữ số bé nhất nên chữ số hàng nghìn là 0.

+ Chữ số hàng trăm là 8.

+ Chữ số hàng chục là chữ số bé nhất nên chữ số hàng chục là 0.

+ Chữ số hàng đơn vị là 3.

Vậy số bé nhất có sáu chữ số mà chữ số hàng trăm là 8 và chữ số hàng đơn vị là 3 là 100 803.

Do đó ta chọn phương án C.

Câu 50: Tìm hiệu của hai số, biết rằng nếu bớt 354 đơn vị ở số bị trừ và thêm 75 đơn vị vào số trừ thì được hiệu mới bằng 2006.

Lời giải:

Nếu bớt 354 đơn vị ở số bị trừ và thêm 75 đơn vị vào số trừ thì hiệu giảm số đơn vị là: 354 + 75 = 429 (đơn vị).

Hiệu của hai số là: 2006 + 429 = 2435.

Đáp số: 2435.

Câu 51: Biết a + 4b chia hết cho 13 (a, b ∈ ℕ). Chứng minh rằng 10a + b chia hết cho 13.

Lời giải:

Ta có a + 4b chia hết cho 13.

Suy ra 10(a + 4b) chia hết cho 13.

Do đó 10a + 40b chia hết cho 13.

Vì vậy 10a + b + 39b chia hết cho 13.

Vì 39 chia hết cho 13 nên 39b chia hết cho 13.

Vậy 10a + b chia hết cho 13.

Câu 52: Biết rằng 75% của một số là 15. Tìm số đó.

Lời giải:

Số cần tìm là: 15 : 75 × 100 = 20.

Đáp số: 20.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: