1500 câu hỏi ôn tập môn Toán có đáp án (Phần 37)

1500 câu hỏi ôn tập Toán (Phần 37)

Câu 1: Cho hàm số y = 2x + 3 có đồ thị là đường thẳng (d). Vẽ đồ thị của hàm số đã cho. Tìm tọa độ giao điểm của đường thẳng (d) với hai trục tọa độ.

Lời giải:

Với x = 0 thì y = 3 Þ điểm (0; 3) thuộc (d).

Với x = –1 thì y = 1 ⇔ điểm (–1; 1) thuộc (d).

Đồ thị hàm số y = 2x + 3 đi qua hai điểm (0; 3) và (–1; 1)

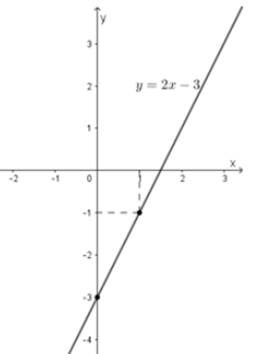
Giao điểm của (d) với trục hoành có tung độ bằng 0 nên y = 0

Khi đó 2x + 3 = 0

Hay $x=\frac{-3}{2}$

Giao điểm của (d) với trục tung có hoành độ bằng 0 nên x = 0

Khi đó 2 . 0 + 3 = y

Hay y = 3

Vậy giao điểm của (d) với trục hoành là $\left(\frac{-3}{2};0\right)$, với trục tung là (0; 3).

Câu 2: Gieo hai đồng tiền xu cân đối và đồng chất. Xác suất để xuất hiện hai mặt ngửa là bao nhiêu?

Lời giải:

Ta có không gian mẫu  W = {SS; NN; SN; NS}.

Suy ra n(Ω) = 4

Gọi biến cố xuất hiện hai mặt ngửa là A.

Do đó A = {NN}, suy ra n(A) = 1.

Vậy xác suất để xuất hiện hai mặt ngửa là $\frac{1}{4}$.

Câu 3: Tìm m để 2 đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Lời giải:

Để (d) và (d’) cắt nhau thì m + 2 ≠ 3 Û m ≠ 1.

Hoành độ giao điểm của (d) và (d’) là nghiệm của phương trình

(m + 2)x + 2m² + 1 = 3x + 3

⇔ (m + 2)x – 3x = 3 – 2m² – 1

⇔ (m – 1)x = 2 – 2m²

⇔ (m – 1)x = 2(1 – m)(1 + m)

$\iff x=\frac{\left(1-m\right)\left(1+m\right)}{\left(m-1\right)}=-m-1$ (do m ≠ 1)

Hai đường thẳng (d) và (d’) cắt nhau trên trục tung suy ra x = 0

⇔ – 1 – m = 0

⇔ – 1 = m (thỏa mãn)

Vậy m = – 1.

Câu 4: Cho đường thẳng d₁: y = 3mx – m² và d₂: y = 3x + m – 2. Tìm m để d₁ và d₂ cắt nhau tại một điểm trên trục tung.

Lời giải:

Để d₁ và d₂ cắt nhau thì 3m ≠ 3 Û m ≠ 1.

Phương trình hoành độ giao điểm của d₁ và d₂ là:

3mx – m² = 3x + m – 2

⇔ (3m – 3)x = m² + m – 2

$\iff x=\frac{m^2+m-2}{3m-3}$ (do m ≠ 1)

$\iff x=\frac{\left(m-1\right)\left(m+2\right)}{3\left(m-1\right)}=\frac{m+2}{3}$

Để d₁ và d₂ cắt nhau tại một điểm trên trục tung thì hoành độ giao điểm bằng 0

$\iff \frac{m+2}{3}=0\iff m=-2\left(tm\right)$

Vậy m = – 2.

Câu 5: Hình dưới đây có bao nhiêu hình tam giác, bao nhiêu hình tứ giác?

A. 4 hình tam giác, 5 hình tứ giác;

B. 4 hình tam giác, 4 hình tứ giác;

C. 5 hình tam giác, 4 hình tứ giác;

D. 5 hình tam giác, 5 hình tứ giác.

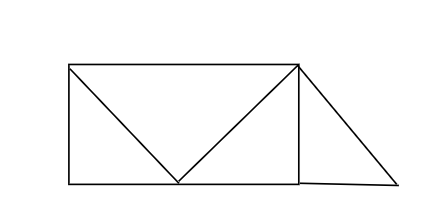
Lời giải:

Trong hình vẽ trên có 5 hình tam giác và 5 hình tứ giác

Vậy ta chọn đáp án D.

Câu 6: Một mảnh vườn hình chữ nhật được chia làm 2 phần để trồng hành và trồng cà rốt. Trong đó diện tích trồng cà rốt gấp 5 lần diện tích trồng hành, chu vi đất trồng cà rốt lớn hơn chu vi đất trồng hành 936 m. Biết chiều rộng mảnh vườn ban đầu là 327 m. Hỏi chu vi mảnh ruộng ban đầu là bao nhiêu dam?

Lời giải:

Vì diện tích trồng cà rốt gấp 5 lần diên tích trồng hành nên cạnh còn lại của diện tích trồng cà rốt gấp 5 lần cạnh còn lại của phần trồng hành

Cạnh còn lại của diện tích trồng hành là:

936 : 2 : (5 – 1) × 1 = 117 (m)

Cạnh còn lại của diện tích trồng cà rốt là:

117 × 5 = 585 (m)

Chiều dài của mảnh đất ban đầu là:

117 + 585 = 702 (m)

Chu vi mảnh ruộng ban đầu là

(702 + 327) × 2 = 2058 (m) = 205,8 (dam)

Vậy chu vi mảnh ruộng ban đầu là 205,8 dam.

Câu 7: Một mảnh vườn hình chữ nhật được chia thành hai phần là hai hình bằng nhau có cạnh 4m. Tính chu vi mảnh vườn hình chữ nhât.

Lời giải:

Chiều dài của mảnh vườn đó là:

4 + 4 = 8 (m)

Chu vi của mảnh vườn đó là:

(8 + 4) × 2 = 24 (m)

Vậy chu vi mảnh vườn đó là 24 m.

Câu 8: Tính nhanh:

a) – (– 2012 + 789) + (– 211) + (– 1012 – 1789).

b) – 72 . 17 + 72 . 31 – 72 . 114.

c) 512 . (2 – 128) – 128 . (– 512)..

d) 120 . (5 – 117) – 117 . (– 120)

Lời giải:

a) – (– 2012 + 789) + (– 211) + (– 1012 – 1789)

= 2012 – 789 – 211 – 1012 – 1789 

= ( 2012 – 1012 ) – 789 – 1789 – 211 

= 1000  – 211 – 789 – 1789 

= 789 – 789 – 1789 

= 0 – 1789

= – 1789.

b) – 72 . 17 + 72 . 31 – 72 . 114

= – 72 . (17 + 114 – 31)

= – 72 . (131 – 31)

= – 72 . 100

= – 7200.

c) 512 . (2 – 128) – 128 . (– 512)

= 512 . 2 – 512 . 128 + 128 . 512

= 512 . 2 + 0

= 1024.

d) 120 . (5 – 117) – 117 . (– 120)

= 120 . 5 – 120 . 117 + 117 . 120

= 120 . 5 – 0

= 600.

Câu 9: Ba tổ công nhân có mức sản xuất tỉ lệ với 5, 4, 3. Tổ I tăng năng suất lên 10%, tổ II tăng năng suất lên 20%, tổ III tăng năng suất lên 10%. Do đó trong cùng một thời gian, tổ I làm được nhiều hơn tổ II là 7 sản phẩm. Tính số sản phẩm mỗi tổ làm được trong thời gian đó.

Lời giải:

Vì mức sản xuất của 3 tổ công nhân tỉ lệ với 5; 4; 3 nên ta gọi mức sản xuất của 3 tổ lần lượt là 5a; 4a; 3a ( với a ∈ ℕ và a > 0)

Tổ I tăng năng suất 10% , tổ II tăng năng suất 20%, tổ III tăng năng suất 10% nên mức sản xuất của 3 tổ là:

• Tổ I: 5a + 5a . 10 % = 5,5a;

• Tổ II: 4a + 4a . 20 % = 4,8a;

• Tổ III: 3a + 3a . 10% = 3,3a.

Trong cùng 1 thời gian, tổ I làm nhiều hơn tổ II 7 sản phẩm nên:

5,5a – 4,8a = 7

⇔ 0,7a = 7

⇔ a = 10

Số sản phẩm tổ I làm trong thời gian đó là: 10.5,5 = 55 (sản phẩm).

Số sản phẩm tổ II làm trong thời gian đó là: 10.4,8 = 48 (sản phẩm).

Số sản phẩm tổ III làm trong thời gian đó là: 10.3,3 = 33 (sản phẩm).

Câu 10: Cho 2 hàm số bậc nhất: y = mx + 3 và y = (2m + 1)x – 5. Tìm giá trị m để đồ thị của hai hàm số đã cho là:

a) hai đường thẳng song song.

b) hai đường thẳng cắt nhau.

Lời giải:

Điều kiện để hai hàm số là hàm số bậc nhất: m ≠ 0, $m\ne \frac{-1}{2}$ .

a) Hai đường thẳng đã cho là hai đường thẳng song song

$\iff \left\{\begin{array}{l}m=2m+1\\ 3\ne -5\end{array}\right.\iff m=-1$ (thỏa mãn)

Vậy m = – 1.

b) Hai đường thẳng đã cho là hai đường thẳng cắt nhau

⇔ m ≠ 2m + 1

⇔ m ≠ – 1 

Vậy m ≠ 0, $m\ne \frac{-1}{2}$ , m ≠ – 1.

Câu 11: Cho tam giác ABC nhọn (AB < AC), đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Tính AH, MH biết AM = 8 cm; BM = 2 cm.

Lời giải:

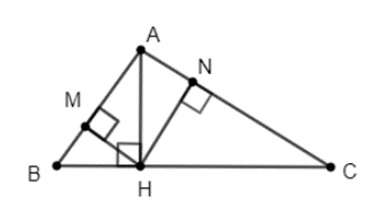
Xét ∆AHB vuông tại H có đường cao MH, theo hệ thức lượng trong tam giác vuông ta có: MH² = MB . MA

Do đó $MH=\sqrt{8.2}=\sqrt{16}=4$ (cm)

Áp dụng định lý Py−ta−go vào ∆AMH vuông tại M, ta có:

$\text{A}H=\sqrt{A{M}^2+M{H}^2}=\sqrt{8^2+4^2}=4\sqrt{5}$ (cm)

Vậy  $AH=4\sqrt{5}$ cm; MH = 4 cm.

Câu 12: Tìm tất cả giá trị thực của tham số m để tập hợp (1; m) chứa đúng hai số nguyên dương.

Lời giải:

Gọi a, b là 2 số nguyên dương thỏa mãn thuộc (1; m) với b > a

Suy ra a, b thỏa mãn 1 < a < b < m

Để (1; m) có đúng 2 số nguyên dương thì a, b là 2 và 3; nên m ∈ (3; 4]

Vậy m ∈ (3; 4].

Câu 13: Xét sự đơn điệu của hàm số $y=-\frac{1}{x}$ .

Lời giải:

Điều kiện xác định x ≠ 0.

Ta có $y=-\frac{1}{x}$

Suy ra $y^{\text{'}}=\frac{1}{x^2}>0$  với mọi x ≠ 0

Vậy y đồng biến trên (– ∞; 0) và (0; + ∞).

Câu 14: Có 4 bao tải gạo, bao thứ hai nặng gấp đôi bao thứ nhất, bao thứ ba nặng hơn bao thứ hai 12,5 kg, bao thứ tư ít hơn bao thứ ba 6,3 kg. Biết rằng cả 4 bao có tất cả 53,7 kg gạo. Hỏi bao thứ ba có bao nhiêu kg gạo?

Lời giải:

Bao thứ 4 có nhiều hơn bao thứ 2 là:

12,5 − 6,3 = 6,2 (kg)

7 lần bao thứ nhất là: 

53,7 − 12,5 − 6,2 = 35 (kg) 

Bao thứ nhất nặng: 

35 : 7 = 5 (kg)

Bao thứ 3 nặng: 

5 × 2 + 12,5 = 22,5 (kg) 

Vậy bao thứ 3 nặng là 22,5 kg.

Câu 15: Tom và Jerry chơi trò chơi bốc kẹo. Ban đầu trên bàn có 24 chiếc kẹo. Bắt đầu từ Tom, hai bạn luân phiên nhau bốc kẹo, mỗi lần được bốc từ 1 đến 5 chiếc kẹo. Ai lấy được chiếc kẹo cuối cùng là người thắng cuộc. Biết cả hai đều chơi thông minh, hỏi ai là người thắng cuộc?

Lời giải:

Vì 24 chia hết cho 6 nên Tom có lấy đi bao nhiêu thì Jerry cũng chỉ cần lấy 6 trừ đi số kẹo Tom vừa lấy (ví dụ : Tom lấy 2 cái, Jerry lấy 4 cái)

Vậy Jerry là người thắng cuộc.

Câu 16: Trong mặt phẳng Oxy, cho đường thẳng d: 2x – y = 0. Phương trình đường thẳng qua phép đồng dạn có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = – 2 và phép đối xừng trục Oy là đường thẳng nào sau đây?

A. – 2x – y = 0;

B. 2x – y = 0;

C. 4x – y = 0;

D. 2x + y – 2 = 0.

Lời giải:

Đáp án đúng là: A

Ta có V_{(O; – 2)} (d) = d’

Suy ra d’ // d hoặc d’ ≡ d

Khi đó phương trình đường thẳng d’ có dạng 2x – y + m = 0

Chọn N(1; 2) thuộc đường thẳng d

Qua V_{(O; – 2)} (N) = N’(–2; – 4) thuộc đường thẳng d’

Suy ra – 4 + 4 + m = 0

Hay m = 0

Do đó phương trình đường thẳng d’ là 2x – y = 0

Qua phép đối xứng trục Oy: D_oy (d’) = d”

Gọi M(x; y) thuộc đường thẳng d’

D_oy (M) = M’(x’; y’) ∈ d”

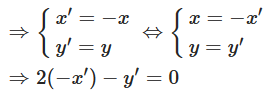
Suy ra phương trình đường thẳng d” là – 2x – y = 0

Vậy ta chọn đáp án A.

Câu 17: Tính A = (x – 2)(x⁴ + 2x³ + 4x² + 8x + 16) tại x = 3.

Lời giải:

Thay x = 3 vào A ta có

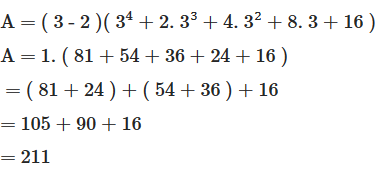
Vậy với x = 3 thì A = 211.

Câu 18: Cho các tập hợp A = (–2; 10), B = (m; m + 2). Tìm m để tập hơp A ∩ B là một khoảng:

A. – 4 < m < 10;

B. – 4 < m ≤ 2;

C. – 4 ≤ m ≤ 10;

D. – 4 < m < 2.

Lời giải:

Đáp án đúng là: A

• Nếu $\left[\begin{array}{l}m+2\le -2\\ 10\le m\end{array}\right.\iff \left[\begin{array}{l}m\le -4\\ m\ge 10\end{array}\right.$  thì A ∩ B = ∅;

• Nếu  $\left\{\begin{array}{l}m\le -2\\ -2<m+2\le 10\end{array}\right.\iff \left\{\begin{array}{l}m\le -2\\ m+2>-2\\ m+2\le 10\end{array}\right.\iff \left\{\begin{array}{l}m\le -2\\ m>-4\\ m\le 8\end{array}\right.\iff -4<m\le -2$

Thì A ∩ B = (–2; m + 2);

• Nếu $\left\{\begin{array}{l}m\le -2\\ 10\le m+2\end{array}\right.\iff \left\{\begin{array}{l}m\le -2\\ m\ge 8\end{array}\right.\left(vôlí\right)$

• Nếu $\left\{\begin{array}{l}-2\le m\\ m+2\le 10\end{array}\right.\iff \left\{\begin{array}{l}m\ge -2\\ m\le 8\end{array}\right.\iff -2\le m\le 8$  thì A ∩ B = (m; m + 2);

• Nếu $\left\{\begin{array}{l}-2\le m<10\\ 10\le m+2\end{array}\right.\iff \left\{\begin{array}{l}-2\le m<10\\ m\ge 8\end{array}\right.\iff 8\le m<10$  thì A ∩ B = (m; 10).

Kết hợp các trường hợp ta có –4 < m < 10 thỏa mãn yêu cầu đề bài

Vậy ta chọn đáp án A.

Câu 19: Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Lời giải:

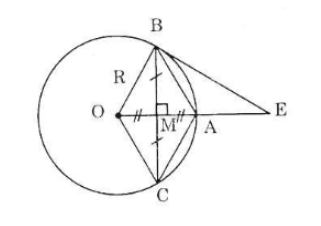
a) Bán kính OA vuông góc với BC nên MB = MC

Lại có MO = MA (giả thiết)

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường

Mà OA ⊥ BC nên OBAC là hình thoi

Vậy OCAB là hình thoi.

b) Vì OCAB là hình thoi nên OB = BA

Mà OA = OB, suy ra OA = OB = BA

Do đó ΔAOB đều, suy ra $\widehat{AOB}=60°$

Trong tam giác OBE vuông tại B ta có:

$BE=OB.\tan \widehat{AOB}=R.\tan 60°=R\sqrt{3}$

Vậy $BE=R\sqrt{3}$ .

Câu 20: Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C’.

Lời giải:

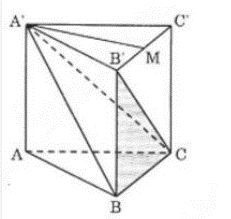
Ta chia khối lẳng trụ đã cho thành hình chóp A’.ABC, C.A’B’C’ và C.A’BB’

Ta có: $V_{A\text{'}.ABC}=V_{C.A\text{'}B\text{'}C\text{'}}=\frac{1}{3}.S.h$

trong đó S là diện tích đáy S = S_ABC = S_A’B’C’ và h là chiều cao của hình lăng trụ

Lại có: V _{ABC.A’B’C’} = S.h

Suy ra

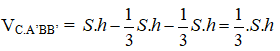
Trong đó, tam giác ABC là tam giác đều có độ dài cạnh bằng a nên

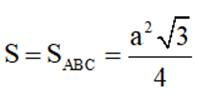
Vì đây là hình lăng trụ đứng nên h = AA’ = BB’ = CC’ = a

Thể tích khối tứ diện A’BB’C’là:

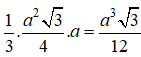
Vậy thể tích khối tứ diện A’BB’C’là $\frac{a^2\sqrt{3}}{12}.$

Câu 21: Cho tam giác ABC có M, N lần lượt là trung điểm của AC, AB. Gọi E là điểm đối xứng với B qua M; F là điểm đối xứng với C qua N.

a) Chứng minh tứ giác ABCE là hình bình hành.

b) Chứng minh E đối xứng với F qua A.

Lời giải:

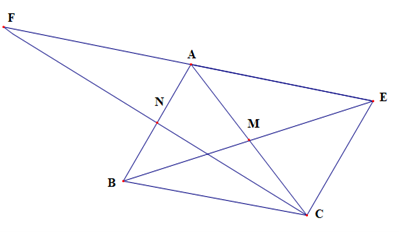
a) Xét tứ giác ABCE có: M là trung điểm của AC và M là trung điểm của BE.

Do đó ABCE là hình bình hành.

b) Vì ABCE là hình bình hành nên BC = AE, BC // AE

Xét tứ giác ACBF có: M là trung điểm của AB và M là trung điểm của CF

Do đó ACBF là hình bình hành

Suy ra BC = AF, BC // AF

Vì BC // AE, BC // AF nên A, E, F thẳng hàng

Mà AE = AF (= BC)

Suy ra E đối xứng với F qua A

Vậy E đối xứng với F qua A.

Câu 22: Tìm x biết: sin²x + sin² 2x + sin² 3x = 2.

Lời giải:

Ta có

Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tìm giao điểm Q của SD và (MNP).

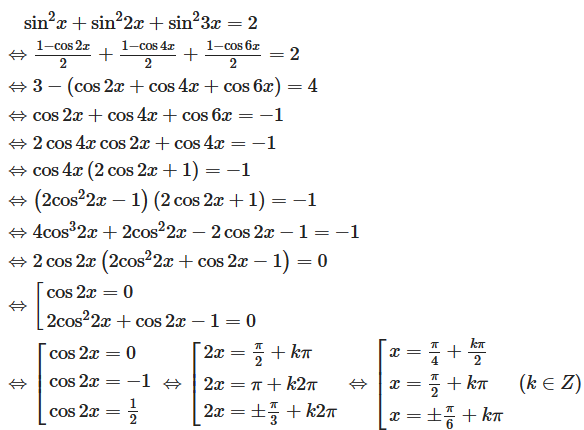
Lời giải:

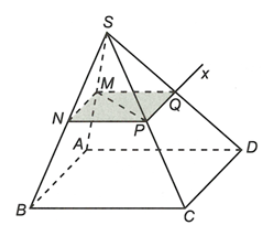
Xét tam giác SAB có M, N là trung điểm SA, SB

Suy ra MN là đường trung bình

Do đó MN // AB

Mà AB // DC (vì ABCD là hình bình hành)

Suy ra MN // CD

Xét (MNP) và (SDC) có P là điểm chung và MN // CD (chứng minh trên)

Suy ra giao tuyến qua P song song với MN, giao với SD tại Q

Do đó SD ∩ (MNP) = PQ.

Câu 24: Cho x × 16 + 4236 = 8860. Khi đó x là bao nhiêu?

Lời giải:

Ta có:

x × 16 + 4236 = 8860

x × 16 = 4624

x = 4624 : 16

x = 289

Vậy x  = 289.

Câu 25: Tính nhanh giá trị của đa thức:

a) ${\text{x}}^2+\frac{1}{2}x+\frac{1}{16}$  tại x = 49,75.

b) x² – y² – 2y – 1 tại x = 93 và y = 6.

Lời giải:

a) Ta có

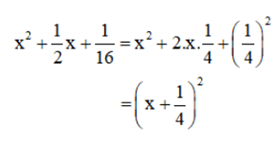
Thay x = 49,75 vào biểu thức ta có giá trị của biểu thức là

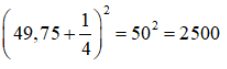
b) Ta có:

x² – y² – 2y – 1

= x² – (y² + 2y + 1)

= x² – (y + 1)²

= (x – y – 1)(x + y + 1)

Thay x = 93, y = 6 ta có

x² – y² – 2y – 1 = (93 – 6 – 1)(93 + 6 + 1) = 86 . 100 = 8 600.

Câu 26: Trên bàn có một số cái bánh, Dương ăn $\frac{5}{8}$  cái bánh, My ăn $\frac{7}{12}$  cái bánh, Lan ăn $\frac{9}{5}$ cái bánh. Hỏi trên bàn có ít nhất bao nhiêu cái bánh?

Lời giải:

Trên bàn có ít nhất số cái bánh là:

$\frac{5}{8}+\frac{7}{12}+\frac{9}{5}=\frac{361}{120}$ (cái)

Vì $3<\frac{361}{120}<4$  nên trên bàn có ít nhất 4 cái bánh

Vậy trên bàn có ít nhất 4 cái bánh.

Câu 27: Cho hai tập hợp A = [m + 1; m + 4] và B = ( – ∞; 5). Tìm tất cả các giá trị của m để A ∩ B = ∅

A. m < 4;

B. m ≥ 4;

C. m > 4;

D. m ≤ 4.

Lời giải:

Đáp án đúng là: B

Để A ∩ B = ∅ thì m + 1 ≥ 5 ⇔ m ≥ 4.

Vậy ta chọn đáp án B.

Câu 28: Cho tam giác ABC cân tại A, đường cao AD, trực tâm H. Tính độ dài AD biết AH = 14 cm, BH = HC = 30 cm.

Lời giải:

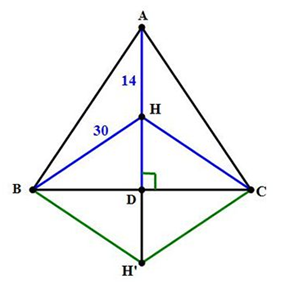
Gọi H’ là điểm đối xứng H qua BC.

Suy ra D là trung điểm của HH’

Vì tam giác ABC cân tại A, AD là đường cao nên AD là trung tuyến

Suy ra D là trung điểm của BC

Xét tứ giác BHCH’ có

D là trung điểm của HH’ và BC;

BC và HH’ là hai đường chéo

Suy ra BHCH’ là hình bình hành.

Mà BH = CH nên hình bình hành BHCH’ là hình thoi

Do đó BH’ // CH, BH = BH’.

Lại có CH ⊥ AB (vì H là trực tâm của tam giác ABC) nên BH’⊥ AB

Hay tam giác ABH’ vuông tại B

Mà BD ⊥ AH’

Suy ra H’B² = H’D . H’A

⇔ HB² = HD . (2HD + HA)

⇔ 30² = HD . (2HD + 14)

⇔ 2HD² + 14HD – 900 = 0

⇔ (HD + 25)(HD – 18) = 0

⇔ HD – 18 = 0 (vì HD > 0)

⇔ HD = 18

Ta có AD = AH + HD = 14 + 18 = 32 cm

Vậy AD = 32 cm.

Câu 29: Cho (d₁): y = – x + 1, (d₂): y = x + 1, (d₃): y = – 1. Gọi A, B, C lần lượt là giao điểm của (d₁) và (d₂); (d₂) và (d₃), (d₁) và (d₃). Tìm tọa độ các điểm A, B, C.

Lời giải:

• Phương trình hoành độ giao điểm của (d₁) và (d₂) là

– x + 1 = x + 1

⇔ x + x = 1 – 1

⇔ 2x = 0

⇔ x = 0

Suy ra y = – 0 + 1 = 1.

Vậy A(0; 1) là tọa độ giao điểm của (d₁) và (d₂).

• Phương trình hoành độ giao điểm của (d₂) và (d₃) là

x + 1 = – 1

⇔ x = – 1 – 1

⇔ x = – 2

Suy ra y = – 1

Vậy B(–2; –1) là tọa độ giao điểm của (d₂) và (d₃).

• Phương trình hoành độ giao điểm của (d₁) và (d₃) là

– x + 1 = – 1

⇔ x = 1 + 1

⇔ x = 2

Suy ra y = – 1

Vậy C(2; –1) là tọa độ giao điểm của (d₁) và (d₃).

Câu 30: Giải phương trình sin²x – cosx + 1 = 0.

Lời giải:

Ta có sin²x – cosx + 1 = 0

⇔ 1 – cos²x  – cosx + 1 = 0

⇔ cos²x  + cosx – 2 = 0

⇔ (cosx + 2)(cosx – 1) = 0

⇔ cosx – 1 = 0 (vì cosx + 2 > 0 với mọi x)

⇔ cosx = 1

⇔ x = k2π (k ∈ ℤ).

Vậy x = k2π (k ∈ ℤ).

Câu 31: Tính giá trị biểu thức P = sin² 10° +  sin² 20° +  sin² 30° + … +  sin² 80° là

A. P = 1;

B. P = 2;

C. P = 4;

D. P = 6.

Lời giải:

Đáp án đúng là: C

Ta có nhận xét sau:

10° + 80° = 20° + 70° = 30° + 60° = 40° + 50° = 90°

Nên các cung lượng giác tương ứng đôi một phụ nhau

Do các góc phụ nhau thì sin góc này bằng cosin góc kia nên ta có:

P = (sin² 10° + sin² 80°) + (sin² 20° + sin² 70°) + ...+ (sin² 40° + sin² 50°)

= (sin² 10° + cos² 10°) + (sin² 20° + cos² 20°) + ...+ (sin² 40° + cos² 40°)

= 1 + 1 + 1 + 1 = 4.

Vậy ta chọn đáp án C.

Câu 32: Tìm nghiệm của phương trình: sin²x = 1.

Lời giải:

Ta có sin²x = 1

 $$\begin{gathered} \iff \left[\begin{array}{l}\mathrm{s}\text{inx}=1\\ \mathrm{s}\text{inx}=-1\end{array}\right. \\ \iff \left[\begin{array}{l}\text{x}=\frac{\pi }{2}+k2\pi \\ \text{x}=-\frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

Vậy $\text{x}=\frac{\pi }{2}+k2\pi$  hoặc $\text{x}=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ .

Câu 33: Tam giác ABC có AB = 3; AC = 6 và góc A = 60°. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

A. 2;

B. 3;

C. 5;

D. 6.

Lời giải:

Đáp án đúng là: B

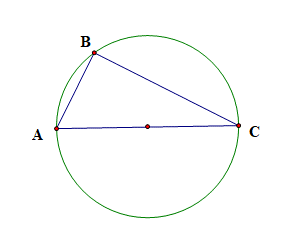
Áp dụng định lí Cosin, ta có

BC² = AB² + AC² – 2AB . AC . cosA = 3² + 6² – 2 . 3 . 6 . cos60° = 27

Ta thấy:  BC² + AB²  = 27 + 9 = 36 = 6² = AC²

Suy ra tam giác ABC vuông tại B

Do đó bán kính đường tròn ngoại tiếp tam giác ABC là

R = AC : 2 = 3

Vậy ta chọn đáp án B.

Câu 34: Trong một trang trại, số gà chiếm $\frac{3}{5}$  tổng số con, số vịt chiếm $\frac{1}{6}$  tổng số con, còn lại là ngỗng. Nhận xét nào sau đây là đúng?

A. Số vịt trong trang trại nhiều hơn số ngỗng;

B. Số vịt trong trang trại nhiều hơn số gà;

C. Số ngỗng trong trang trại nhiều hơn số vịt;

D. Số vịt trong trang trại bằng số ngỗng.

Lời giải:

Đáp án đúng là: C

Số ngỗng chiếm số phần là

$1-\frac{3}{5}-\frac{1}{6}=\frac{30-18-5}{30}=\frac{7}{30}$ (tổng số con)

Ta có $\frac{1}{6}<\frac{7}{30}<\frac{3}{5}$

Suy ra số ngỗng trong trang trại nhiều hơn số vịt

Vậy ra chọn đáp án C.

Câu 35: Cho phương trình x² – 3(m – 1)x + 2m – 4 = 0. Tìm m để phương trình có một nghiệm x = 2 và tìm nghiệm còn lại.

Lời giải:

Thay x = 2 vào phương trình ta có

2² – 3(m – 1) . 2 + 2m – 4 = 0

⇔ 4 – 6m + 6 + 2m – 4 = 0

⇔ 6 – 4m = 0

⇔ $m=\frac{3}{2}$

Thay $m=\frac{3}{2}$  vào phương trình ta có

${\text{x}}^2-3\left(\frac{3}{2}-1\right)x+2.\frac{3}{2}-4=0$

⇔ ${\text{x}}^2-\frac{3}{2}x-1=0$

⇔ 2x² – 3x – 2 = 0

⇔ (x – 2)(2x + 1) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}x-2=0\\ 2\text{x}+1=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=2\\ x=\frac{-1}{2}\end{array}\right. \end{gathered}$$

Vậy $m=\frac{3}{2}$  thỏa mãn yêu cầu đề bài và nghiệm còn lại là $\text{x}=\frac{-1}{2}$ .

Câu 36: Tính giá trị của A = (x – 3)² – (x + 1)³ + 12x(x – 1) với $x=\frac{-1}{2}$ .

Lời giải:

Thay $x=\frac{-1}{2}$  vào biểu thức A ta có

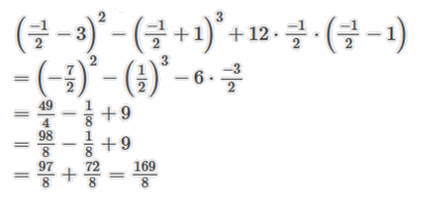
Vậy $\text{A}=\frac{169}{8}.$

Câu 37: Chọn ngẫu nhiên 3 số từ tập S = {1; 2; ... ; 11}. Tính xác suất để tổng ba số được chọn là 12.

Lời giải:

Ta có $n\left(\Omega \right)=C_{11}^3=165$

Gọi A là biến cố “Chọn ngẫu nhiên 3 số từ tập S sao cho tổng 3 số là 12”

A = {(1, 2, 9); (1, 3, 8); (1, 4, 7); (1, 5, 6); (2, 3, 7); (2, 4, 6); (3, 4, 5)}.

Suy ra n(A) = 7.

Vậy $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{7}{165}.$

Câu 38: Có tất cả bao nhiêu số tự nhiên có 5 chữ số khác nhau mà trong đó mỗi số luôn có mặt 2 chữ số lẻ và 3 chữ số chẵn?

Lời giải:

Gọi số cần tìm là $\overline{abc\text{d}e}$

• Nếu a là số chẵn

Giả sử b, c là số chẵn và d, e là số lẻ

+ Chọn số cho a có 4 cách (2 ; 4 ; 6 ; 8)

+ Chọn số cho b có 3 cách 

+ Chọn số cho c có 2 cách 

+ Chọn số cho d có 5 cách

+ Chọn số cho e có 4 cách 

Suy ra nếu a là số chẵn thì sẽ có 4 . 3 . 2 . 5 . 4 = 480 số

• Nếu a là số lẻ

Giả sử b là số lẻ và c, d, e là số chẵn

+ Chọn số cho a có 5 cách

+ Chọn số cho b có 4 cách

+ Chọn số cho c có 5 cách

+ Chọn số cho d có 4 cách

Chọn số cho e có 3 cách

Vậy khi a là số lẻ thì có 5 . 4 . 5 . 4 . 3 = 1200 (số)

Vậy có 1200 + 480 = 1680 số thỏa mãn yêu cầu đề bài

Câu 39: Qua đỉnh C của hình bình hành ABCD kẻ đường thẳng song song với BD, cắt AB ở E, cắt AD ở F.

a) Tứ giác BECD là hình gì? Vì sao?

b) Chứng minh rằng ba đường thẳng AC, BF, DE đồng quy.

Lời giải:

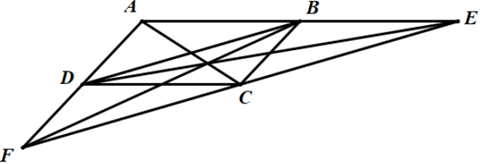
a) Vì ABCD là hình bình hành nên AB // DC, AD // BC

Hay BE // DC

Xét tứ giác BECD có

BE // DC và BD // CE

Suy ra BECD là hình bình hành.

b) Vì ABCD là hình bình hành nên AB = CD

Vì BECD là hình bình hành nên BE = CD

Suy ra AB = BE, BD = CE

Xét tứ giác BCFD có: BD // CF và BC // DF

Suy ra BCFD là hình bình hành.

Do đó DF = BC, DB = CF

Mà BC = AD (vì ABCD là hình bình hành)

Suy ra DA = DF

Ta có BD = CF, BD = CE (chứng minh trên)

Suy ra CF = CE

Xét tam giác AEF có AC, FB, ED là ba đường trung tuyến nên chúng đồng quy

Vậy ba đường thẳng AC, BF, DE đồng quy.

Câu 40: Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?

Lời giải:

+) Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.

+) Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.

Câu 41: Tìm số tự nhiên n, để

a) n + 4 ⋮ n.

b) 5n – 6 ⋮ n (n < 1).

c) 143 – 12n ⋮ n (với n < 12).

Lời giải:

a) Để n + 4 ⋮ n ⇔ 4 ⋮ n

⇔ n  ∈ Ư(4) = {–4; –2; –1; 1; 2 ; 4}

Vậy n ∈ {–4; –2; –1; 1; 2 ; 4}.

b) 5n – 6 ⋮ n (n < 1)

⇔ 6 ⋮ n (vì 5n ⋮ n)

⇔ n  ∈ Ư(6) = {–6; –3; –2; –1; 1; 2 ; 3; 6}

Mà n < 1 nên n ∈ {–6; –3; –2; –1}

Vậy n ∈ {–6; –3; –2; –1}.

c) 143 – 12n ⋮ n (với n < 12).

⇔ 143 ⋮ n (vì 12n ⋮ n)

⇔ n ∈ Ư(143) = {–143; – 13; – 11; – 1; 1; 11 ; 13; 143}

Mà n < 12 nên n ∈ {– 143; – 13; – 11; – 1; 1; 11}

Vậy n ∈ {– 143; – 13; – 11; – 1; 1; 11}.

Câu 42: Cho các số từ 1 đến 9. Em hãy điền các số này vào các ô vuông, sao cho tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau

Lời giải:

Ta điền như bảng sau để được tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau và bằng 15

Câu 43: Cho a là một số tự nhiên chia cho 19 dư 3, b là một số tự nhiên chia cho 38 dư 5. Hỏi 3a + 2b có chia hết cho 19 không?

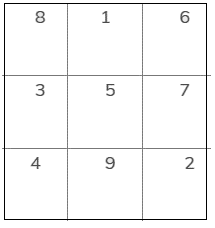
Lời giải:

Vì a chia 19 dư 3 nên a = 19m + 3

Vì b chia 38 dư 5 nên b = 38n + 5

Ta có:

   3a + 2b

= 3(19m + 3) + 2(38n + 5)

= 57m + 9 + 76n + 10

= 57m + 76n + 19

Vì 57m ⋮ 19; 76n ⋮ 19 và 19 ⋮ 19

Suy ra (57m + 76n + 19) ⋮ 19

Vậy 3a + 2b ⋮ 19.

Câu 44: Cho tam giác ABC điểm M nằm trong tam giác. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Gọi A’, B’, C’ thứ tự là điểm đối xứng của M qua D, E, F

a) Chứng minh tứ giác AB’A’B là hình bình hành.

b) Gọi O là giao điểm của AA’ và BB’, chứng minh C và C’ đối xứng nhau qua điểm O.

Lời giải:

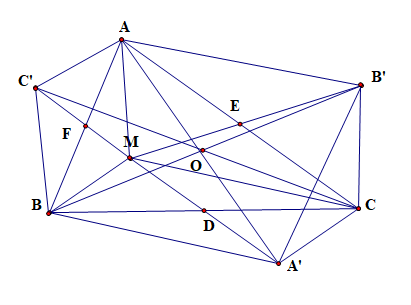
a) Xét tứ giác AB’CM có

AC cắt MB' tại trung điểm E của mỗi đường và AC, MB’ là hai đường chéo

Suy ra AB'CM là hình bình hành

Do đó AB' // MC, AB' = MC

Xét tứ giác BMCA’ có

BC cắt MA' tại trung điểm D của mỗi đường và BC, MA’ là hai đường chéo

Suy ra BMCA' là hình bình hành

Do đó MC // A'B, MC = A'B.

Ta có AB' // MC, MC // A'B (chứng minh trên), suy ra AB’ // A’B.

Ta có MC = A'B, AB' = MC (chứng minh trên), suy ra AB’ = A’B.

Xét tứ giác AB’A’B có AB’ // A’B và AB’ = A’B

Suy ra tứ giác AB'A'B là hình bình hành.

b) Xét hình bình hành AB'A'B có AA’ và BB’ cắt nhau tại O

Suy ra O là trung điểm của AA’.

Chứng minh tương tự câu a ta có: AC’ = A’C (= BM) và AC’ // A’C (// BM)

Suy ra AC’A’C là hình bình hành.

Mà O là trung điểm của AA’

Suy ra O là trung điểm của CC’.

Hay C và C’ đối xứng nhau qua điểm O

Vậy C và C’ đối xứng nhau qua điểm O.

Câu 45: Tìm m, n để đa thức x³ – mx² – n khi chia cho đa thức x – 3 dư là 27 còn khi chia cho đa thức x + 1 được dư là 7.

Lời giải:

Theo đề, ta có x³ – mx² – n khi chia cho đa thức x – 3 dư là 27.

Suy ra x³ – mx² – n = (x – 3)P(x) + 27.

Với x = 3, ta có 27 – 9m – n = 27.

Suy ra n = –9m  (1)

Theo đề, ta lại có x³ – mx² – n khi chia cho đa thức x + 1 được dư là 7.

Suy ra x³ – mx² – n = (x + 1)Q(x) + 7.

Với x = –1, ta có –1 – m – n = 7.

Suy ra m + n = –8   (2)

Thế (1) vào (2), ta được: m – 9m = –8.

Suy ra –8m = –8.

Do đó m = 1.

Thế m = 1 vào (1), ta được n = –9.1 = –9.

Vậy m = 1, n = –9 thỏa mãn yêu cầu bài toán.

Câu 46: Phân tích đa thức sau thành nhân tử: x² + 2x + 1 – 4y².

Lời giải:

x² + 2x + 1 – 4y²

= (x + 1)² – (2y)²

= (x + 1 – 2y)(x + 1 + 2y).

Câu 47: Phân tích đa thức sau thành nhân tử: x² – 2x – 4y² + 1.

Lời giải:

x² – 2x – 4y² + 1

= (x² – 2x + 1) – 4y²

= (x – 1)² – (2y)²

= (x – 1 – 2y)(x – 1 + 2y).

Câu 48: Giải phương trình x² – 2x – 15 = 0.

Lời giải:

x² – 2x – 15 = 0

⇔ (x² – 5x) + (3x – 15) = 0

⇔ x(x – 5) + 3(x – 5) = 0

⇔ (x + 3)(x – 5) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}x+3=0\\ x-5=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=-3\\ x=5\end{array}\right. \end{gathered}$$

Vậy phương trình đã cho có nghiệm là $\left[\begin{array}{l}x=-3\\ x=5\end{array}\right.$ .

Câu 49: Tại sao sinx ≠ 0 ⇔ x ≠ kπ?

Lời giải:

Để giải sinx ≠ 0, trước tiên, ta giải phương trình sinx = 0.

Ta có sinx = 0.

⇔ sinx = sin0.

$$\begin{gathered} \iff \left[\begin{array}{l}x=0+k2\pi \\ x=\pi -0+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \\ \iff \left[\begin{array}{l}x=k2\pi \\ x=\pi +k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

⇔ x = kπ (k ∈ ℤ).

Khi đó sinx = 0 ⇔ x = kπ (k ∈ ℤ).

Vậy sinx ≠ 0 ⇔ x ≠ kπ (k ∈ ℤ).

Câu 50: Tìm x, biết: (4x – 1)² – (x + 7)² = 0.

Lời giải:

(4x – 1)² – (x + 7)² = 0

⇔ (4x – 1 – x – 7)(4x – 1 + x + 7) = 0

⇔ (3x – 8)(5x + 6) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}3x-8=0\\ 5x+6=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=\frac{8}{3}\\ x=-\frac{6}{5}\end{array}\right. \end{gathered}$$

Vậy $x\in \left\{\frac{8}{3};-\frac{6}{5}\right\}$ .

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: