1500 câu hỏi ôn tập Toán (Phần 10)

Câu 1: Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.

a) Chứng minh : tứ giác AOHC nội tiếp.

b) Chứng minh : AC . AE = AD . CE

c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM // BN

Lời giải:

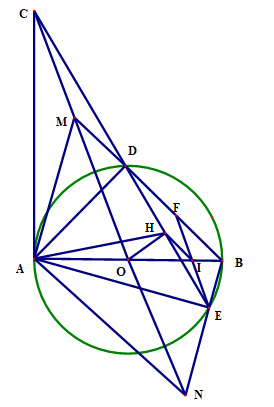
a) Ta có 

$\begin{array}{l}\stackrel{⏜}{\text{CAB}}{\text{ = 90}}^{\text{0}}\\ \stackrel{⏜}{\text{OHC}}{\text{ = 90}}^{\text{0}}\text{}\\ \Rightarrow \stackrel{⏜}{\text{CAB}}\text{ +}\stackrel{⏜}{\text{OHC}}{\text{ = 180}}^{\text{0}}\end{array}$

Vậy tứ giác AOHC nội tiếp.                                                   

b) Ta có $\stackrel{⏜}{\text{CAD}}\text{ = }\stackrel{⏜}{\text{AEC}}\text{, }\stackrel{⏜}{\text{ACE}}$ chung suy ra $\text{ΔACD ~ ΔECA}$ (g.g)

$\Rightarrow \frac{\text{CA}}{\text{CE}}\text{ = }\frac{\text{AD}}{\text{AE}}\Rightarrow \text{AC . AE = AD . CE}$

c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F

$\Rightarrow \stackrel{⏜}{\text{HEI}}\text{ = }\stackrel{⏜}{\text{HCO}}$

Vì tứ giác AOHC nội tiếp $\Rightarrow \stackrel{⏜}{\text{HAO}}\text{ = }\stackrel{⏜}{\text{HCO}}\text{ = }\stackrel{⏜}{\text{HEI}}$

Suy ra tứ giác AHIE nội tiếp $\Rightarrow \stackrel{⏜}{\text{IHE}}\text{ =}\stackrel{⏜}{\text{ IAE}}\text{ = }\stackrel{⏜}{\text{BDE}}\Rightarrow \text{HI // BD}$

Mà H là trung điểm của DE $\Rightarrow$  I là trung điểm của EF. Có EF // MN và IE =  IF

$\Rightarrow$ O là trung điểm của đoạn thẳng MN.

Suy ra tứ giác AMBN là hình bình hành $\Rightarrow$  AM//BN.

Câu 2: Chọn ngẫu nhiên 5 quân bài trong cỗ bài tú lơ khơ ta được một xấp bài. Tính xác suất để trong xấp bài này chứa hai bộ đôi (tức là có hai con cùng thuộc một bộ, hai con thuộc bộ thứ 2, con thứ 5 thuộc bộ khác).

Lời giải:

Số cách chọn 5 trong 52 quân bài là ${\text{C}}_{\text{52}}^{\text{5}}$ .

Giả sử 5 quân bài này có 2 quân thuộc bộ A, 2 quân thuộc bộ B, 1 quân thuộc bộ C.

Có 52 cách chọn 1 quân bộ C.

Khi đó chỉ được chọn 4 quân còn lại trong số 12 bộ còn lại (bỏ bộ có quân C đi)

Có ${\text{C}}_{\text{12}}^{\text{2}}$ cách chọn 2 trong số 12 bộ còn lại.

Mỗi bộ A, B lại có ${\text{C}}_{\text{4}}^{\text{2}}$ cách chọn.

Vậy có ${\text{52 . C}}_{\text{12}}^{\text{2}}{\text{ . C}}_{\text{4}}^{\text{2}}{\text{ . C}}_{\text{4}}^{\text{2}}\text{ = 123552}$ cách chọn.

Vậy xác suất cần tìm là $\text{P = }\frac{\text{123552}}{{\text{C}}_{\text{52}}^{\text{5}}}$

Câu 3: Cho a, b, c là độ dài 3 cạnh của tam giác. CMR

$\frac{\text{a}}{\text{b + c - a}}\text{ + }\frac{\text{b}}{\text{a + c - b}}\text{ + }\frac{\text{c}}{\text{a + b - c}}\ge \text{3}$

Lời giải:

Đặt $\text{x = b + c - a}$

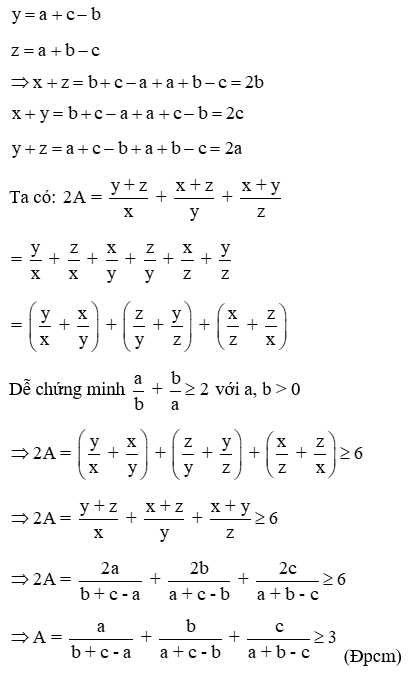
Câu 4: Cho M = 1 x 3 x 5 x 7 x....... x 2023 + 2024. Hỏi M chia cho 5 dư bao nhiêu ?

Lời giải:

$\text{M = 1 × 3 × 5 × 7 × }\mathrm{...}\text{ × 2023 + 2024}$

Xét $\text{1 × 3 × 5 × 7 × }\mathrm{...}\text{ × 2023}$ có thừa số 5

$\Rightarrow \text{1 × 3 × 5 × 7 × }\mathrm{...}\text{ × 2023 }⋮\text{5}$

Có 2024 chia 5 dư 4 (2)

Từ (1) và (2)

$\Rightarrow$M chia cho 5 dư 4

Câu 5: Giải phương trình ${\text{x}}^{\text{2}}\text{ - 2nx - 5 = 0}$. Biết số nguyên dương n thỏa mãn ${\text{C}}_{\text{n}}^{\text{n - 1}}{\text{ + C}}_{\text{5}}^{\text{n}}\text{ = 9}$

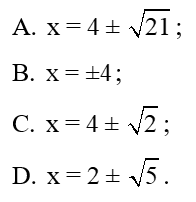
Lời giải:

Đáp án đúng là A

Xét phương trình:  ${\text{C}}_{\text{n}}^{\text{n - 1}}{\text{ + C}}_{\text{5}}^{\text{n}}\text{ = 9}\iff n=4$

Với n = 4 thì phương trình trở thành: x² – 8x – 5 = 0

Suy ra phương trình có hai nghiệm $\text{x = 4 ± }\sqrt{\text{21}}$ .

Câu 6: Một học sinh muốn chọn 20 trong 30 câu trắc nghiệm. Học sinh đó đã chọn được 5 câu. Tìm số cách chọn các câu còn lại ?

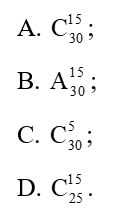
Lời giải:

Trong 30 câu đã chọn 5 câu nên còn lại 25 câu.

Ta cần chọn 15 câu trong 25 câu nên có ${\text{C}}_{\text{25}}^{\text{15}}$  cách chọn.

Câu 7: Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ.

Khẳng định nào sau đây là đúng?

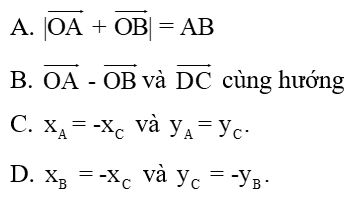
Lời giải:

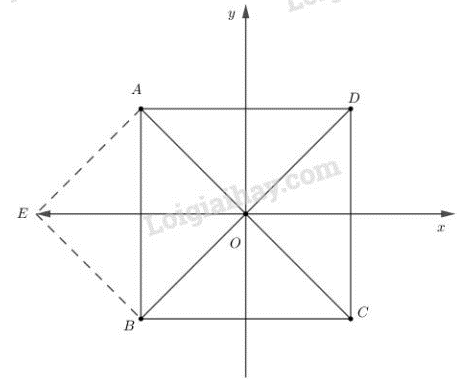
A) Ta có: 

$\begin{array}{l}\overrightarrow{\text{OA}}\text{ + }\overrightarrow{\text{OB}}\text{ = }\overrightarrow{\text{CO}}\text{ + }\overrightarrow{\text{OB}}\text{ = }\overrightarrow{\text{CB}}\\ \Rightarrow \left|\overrightarrow{\text{OA}}\text{ + }\overrightarrow{\text{OB}}\right|\text{ = }\left|\overrightarrow{\text{CB}}\right|\text{ = CB = AB}\end{array}$

A đúng.

B) Vì $\overrightarrow{\text{OA}}\text{ - }\overrightarrow{\text{OB}}\text{ = }\overrightarrow{\text{BA}}$

Mà $\overrightarrow{\text{BA}}$ và $\overrightarrow{\text{DC}}$  ngược hướng nên B) sai

C) Vì ${\text{x}}_{\text{A}}{\text{= -x}}_{\text{C}}{\text{,\hspace{0.33em}\hspace{0.33em}y}}_{\text{A}}{\text{= -y}}_{\text{C}}\Rightarrow \text{C}$ sai.

D) Vì ${\text{x}}_{\text{B}}{\text{= -x}}_{\text{C}}{\text{,\hspace{0.33em}\hspace{0.33em}y}}_{\text{B}}{\text{= y}}_{\text{C}}\Rightarrow \text{D}$ sai.

Chọn A.

Cách giải thích khác:

Qua A kẻ $\overrightarrow{\text{AE}}\text{ = }\overrightarrow{\text{OB}}\Rightarrow \overrightarrow{\text{OA}}\text{ + }\overrightarrow{\text{OB}}\text{ = }\overrightarrow{\text{OA}}\text{ + }\overrightarrow{\text{AE}}\text{ = }\overrightarrow{\text{OE}}$

Ta dễ dàng chứng minh được:

$\overrightarrow{\text{OE}}\text{ = }\overrightarrow{\text{DA}}\Rightarrow \text{|}\overrightarrow{\text{OA}}\text{ + }\overrightarrow{\text{OB}}\text{| = |}\overrightarrow{\text{OE}}\text{| = |}\overrightarrow{\text{DA}}\text{| = |}\overrightarrow{\text{BA}}\text{| = AB}$

Vậy A) đúng.

Câu 8: Trong hệ tọa độ Oxy,  cho ba điểm  A(1; 3); B(-1; 2); C(-2; 1). Tìm tọa độ của vectơ $\overrightarrow{\text{AB}}\text{ - }\overrightarrow{\text{AC}}\text{.}$

A. (-5; -3)

B.  (1; 1)

C. (-1; 2)

D. (-1; 1)

Lời giải:

$\left\{\begin{array}{c}\overrightarrow{AB}=(-2;-1)\\ \overrightarrow{AC}=(-3;-2)\end{array}\right.\Rightarrow \overrightarrow{AB}-\overrightarrow{AC}=(-2-(-3);-1-(-2\left)\right)=(1;1)$

Đáp án B

Câu 9: Tổng của 2 số bằng 10,45. Tìm hai số đó, biết rằng nếu số hạng thứ nhất cộng với 4 lần số hạng thứ hai thì được 22,45.

Lời giải:

Ta gọi 2 số đó là a và b 

Ta có a + b = 10,45                ( 1 )

Theo Đề bài: a + 4b = 22, 45                ( 2)

Lấy (2) - (1) ta có a + 4b - a - b = 22,45 - 10,45 = 12

$\Rightarrow$3b = 12

$\Rightarrow$ b = 4

$\Rightarrow$ a = 10,45-4 = 6,45

Câu 10: Xác định hàm số bậc 2: y =  - 4x + c, biết rằng đồ thị của nó: 

a, Đi qua 2 điểm A (1; 2) và B (2;3)

b, Có đỉnh I (-2;-1)

c, Có hoành độ là -3 và đi qua điểm P (-2;1)

d, Có trục đối xứng là đường thẳng x= 2 và cắt trục hoành tại điểm M (3;0)

Lời giải:

a) Do đường thẳng đi qua 2 điểm A(1; 2) và B(2; 3)

$\Rightarrow$Ta có hệ phương trình

$\left\{\begin{array}{c}2=a-4+c\\ 3=4a-8+c\end{array}\right.\Rightarrow \left\{\begin{array}{c}a=\frac{5}{3}\\ b=\frac{13}{3}\end{array}\right.\Rightarrow y=\frac{5}{3}{x}^2-4x+\frac{13}{3}$

b) Do hàm số có đỉnh I(-2; -1)

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}-\frac{-4}{2a}=-2\\ \frac{-16+4ac}{4a}=-1\end{array}\right.\Rightarrow \left\{\begin{array}{c}-4=4a\\ -16+4ac=-4a\end{array}\right.\Rightarrow \left\{\begin{array}{c}a=-1\\ c=-5\end{array}\right. \\ \Rightarrow y=-x^2-4x-5 \end{gathered}$$

c) Do hàm số có hoành độ đỉnh bằng -3

$\begin{array}{l}\Rightarrow -\frac{-4}{2a}=-3\\ \Rightarrow -4=-6a\\ \Rightarrow a=-\frac{2}{3}\end{array}$

Lại có hàm số đi qua P(-2; 1)

$\Rightarrow$Thay x = -2 và y = 1 vào hàm số ta được

$\begin{array}{l}-\frac{2}{3}.4+8+c=1\\ \Rightarrow c=-\frac{13}{3}\end{array}$

d) Do hàm số có trục đối xứng x = 2

$\begin{array}{l}\Rightarrow -\frac{-4}{2a}=2\\ \Rightarrow 4=4a\\ \iff a=1\end{array}$

Do hàm số cắt trục hoành tại điểm M(3; 0)

$\Rightarrow$Thay x = 3 và y = 0 vào hàm số ta có

9 – 4 . 3 + c = 0

$\Rightarrow$ c = 3

Câu 11: Cho $\Delta$ ABC cân tại A ( $\widehat{A}<{90}^{\circ }$). Vẽ BH $\perp$  AC, CK $\perp$ AB.

a) Chứng minh rằng AH = AK.

b) Gọi I là giao điểm của BH và CK. Chứng minh $\Delta$ BIC cân.

c) Chứng minh HI là tia phân giác của A

Lời giải:

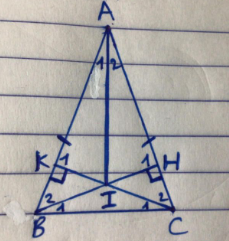
Câu 12: Cho $\Delta$ ABC, lấy điểm M thuộc cạnh AB sao cho $BM=\frac{1}{3}BA$.
Gọi N là trung điểm của cạnh BC. Tính tỉ số $\frac{SBMN}{SABC}$

Lời giải:

N là trung điểm BC $\Rightarrow \text{BN = }\frac{\text{1}}{\text{2}}\text{BC}$

Kẻ đường cao AD và ME ứng với BC $\Rightarrow AD//ME$

Do AD và ME cùng vuông góc BC

Áp dụng định lý Talet:

$\frac{\text{ME}}{\text{AD}}\text{ = }\frac{\text{BM}}{\text{BA}}\text{ = }\frac{\text{1}}{\text{3}}\Rightarrow \text{ME = }\frac{\text{1}}{\text{3}}\text{AD}$

Ta có:

$\frac{{\text{S}}_{\text{BMN}}}{{\text{S}}_{\text{ABC}}}\text{ = }\frac{\frac{\text{1}}{\text{2}}\text{ . ME . BN}}{\frac{\text{1}}{\text{2}}\text{AD . BC}}\text{ = }\frac{\frac{\text{1}}{\text{3}}\text{AD . }\frac{\text{1}}{\text{2}}\text{BC}}{\text{AD . BC}}\text{ = }\frac{\text{1}}{\text{6}}$

Câu 13: Phương trình ${\text{3 . 2}}^{\text{x}}{\text{ - 4}}^{\text{x - 1}}\text{ - 8 = 0}$ có 2 nghiệm x₁, x₂ và có tổng x₁ + x₂ là:

A. 2

B. 3

C. 4

D. 5

Lời giải:

${\text{3 . 2}}^{\text{x}}{\text{ - 4}}^{\text{x - 1}}\text{ - 8 = 0}\iff {\text{3 . 2}}^{\text{x}}\text{ - }\frac{{\text{4}}^{\text{x}}}{\text{4}}\text{ - 8 = 0}\iff {\text{3 . 2}}^{\text{x}}\text{ - }\frac{\text{1}}{\text{4}}{\left({\text{2}}^{\text{x}}\right)}^{\text{2}}\text{ - 8 = 0.}$

Đặt ${\text{2}}^{\text{x}}\text{ = t\hspace{0.17em}\hspace{0.17em}}\left(\text{t > 0}\right)$ khi đó phương trình trở thành

$3t-\frac{1}{4}{t}^2-8=0\iff \left[\begin{array}{c}t=8\left(tm\right)\\ t=4\left(tm\right)\end{array}\right.\iff \left[\begin{array}{c}{2}^x=8\\ 2^x=4\end{array}\right.\iff \left[\begin{array}{c}{x}_1=3\\ x_2=2\end{array}\right.\Rightarrow x_1+x_2=5$

Chọn D

Câu 14: Một lớp có 30 học sinh gồm 12 học sinh nam, 18 học sinh nữ, cần chọn ra 5 học sinh gồm cả nam và nữ đi thi giới thiệu sách. Hỏi có bao nhiêu cách chọn để trong đó có ít nhất 3 nữ?

A. 9800

B. 90576

C. 92760

D. 54600

Lời giải:

Trường hợp 1: Chọn 3 nữ, 2 nam ⇒ có $C_{18}^3{C}_{12}^2$ cách chọn

Trường hợp 2: Chọn 4 nữ, 1 nam có $C_{18}^4{C}_{12}^1$ cách chọn

Do đó có $C_{18}^3{C}_{12}^2+C_{18}^4{C}_{12}^1=90576$ cách chọn.

Chọn B.

Câu 15: Một lớp học có 30 học sinh gồm có nam và nữ. Chọn ngẫu nhiên 3 học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được 2 nam và 1 nữ là $\frac{12}{29}$ . Tính số học sinh nữ của lớp.

A. 16;

B. 14;

C. 13;

D. 17.

Lời giải:

Đáp án đúng là: B

Gọi n là số học sinh nam của lớp (n ∈ ℕ^*; n ≤ 28)

⇒ Số học sinh nữ là 30 – n

Ta có: Mỗi lần chọn 3 học sinh từ 30 học sinh cho ta một tổ hợp chập 3 của 30 nên $\text{n}\left(\text{Ω}\right){\text{ = C}}_{\text{30}}^{\text{3}}\text{= 4060}$

Gọi N là biến cố:” Chọn được 2 học sinh nam và 1 học sinh nữ”

Việc chọn 2 học sinh nam và 1 học sinh nữ có thể xem 1 công việc 2 công đoạn:

- Công đoạn 1: chọn 2 học sinh nam có ${\text{C}}_{\text{n}}^{\text{2}}$

- Công đoạn 2: Chọn 1 học sinh nữ có ${\text{C}}_{\text{30-n}}^{\text{1}}\text{= 30 – n}$  cách

$$\begin{gathered} \Rightarrow \text{ n}\left(\text{N}\right)\text{ = }\left(\text{30 – n}\right){\text{ . C}}_{\text{n}}^{\text{2}} \\ \Rightarrow \text{ P}\left(\text{N}\right)\text{ = }\frac{\text{n(N)}}{\text{n(Ω)}}\text{ = }\frac{\left(\text{30 - - n}\right){\text{ . C}}_{\text{n}}^{\text{2}}}{\text{4060}}\text{ = }\frac{\text{12}}{\text{29}} \\ \Rightarrow \left(\text{30 – n}\right){\text{ . C}}_{\text{n}}^{\text{2}}\text{ = 1680} \end{gathered}$$

Mà ${\text{C}}_{\text{n}}^{\text{2}}\text{ = }\frac{\text{n!}}{\text{2!(n - 2)!}}\text{ = }\frac{\text{(n-2)!.(n - 1) . n}}{\text{2!(n - 2)!}}$

$$\begin{gathered} \begin{array}{l}\Rightarrow \left(\text{30 – n}\right)\text{ . }\frac{\text{n(n - 1)}}{\text{2}}\text{ = 1680}\\ \Rightarrow -n^3 +31n^2 -30n+3360=0\end{array} \\ \Rightarrow \left[\begin{array}{c}{n}_1\approx -\mathrm{8,82}\\ n_2\approx \mathrm{23,82}\\ n_3=16\end{array}\right. \end{gathered}$$

Vì $n \in {\mathbb{N}}^{*};n \le 28$ nên n = 16

Vậy số học sinh nữ của lớp là : 30 – 16 = 14 (học sinh).

Câu 16: Tổng của 2 vectơ đối bằng bao nhiêu?

Lời giải:

Hai vec tơ đối nhau có tổng bằng không.

Câu 17: Hình thang với hai cạnh bên bằng nhau, góc tù bằng 120^o thì có phải là hình thang cân không ?

Lời giải:

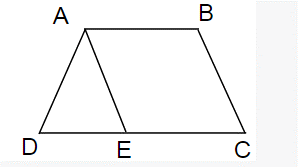
Giả sử: AD = BC; góc DAB = 120^o

Vì AB // CD nên góc DAB + ADC = 180^o 

⇒ góc ADC = 180^o - DAB = 180^o - 120^o = 60^o

Trên đoạn CD lấy E sao cho CE = AB

Mà có: CE // AB ⇒ Tứ giác ABCE là hình bình hành ⇒ AE = BC và AE // BC

AE = BC; BC = AD ⇒ AE = AD → tam giác ADE cân tại A ⇒ $\widehat{ADC}=\widehat{AED}$

mặt khác,  $\widehat{ADC}\text{=}{60}^{o } \Rightarrow \widehat{AED}\text{=}{60}^{o }$

Mà góc AED = BCE (do BC // AE) nên $\widehat{BCE}={60}^o$

$\Rightarrow \widehat{BCE}=\widehat{ADC}\Rightarrow$ ABCD là hình thang cân.

Câu 18: Hình thang có 2 cạnh bên bằng nhau có phải là hình thang cân không? Vì sao?

Lời giải:

Chưa chắc đã là hình thang cân.

Vì hình thang có 2 cạn bên bằng nhau, có 2 góc bằng nhau, thì mới suy ra là hình thang cân.

Câu 19: Cho hàm số y = x² và y = mx + 4, với m là tham số.

a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A₁(x₁,y₁); A₂ (x₁ ,y₂). Tìm tất cả các giá trị của m sao cho (y₁)² + (y₂)² = 7².

Lời giải:

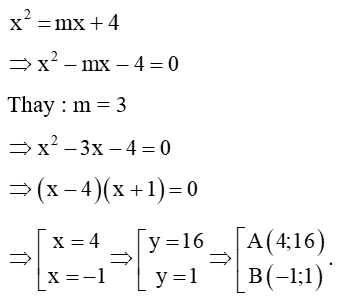
b) Ta có phương trình hoành độ giao điểm:

x² – mx – 4 = 0.

Ta thấy ∆ = m² + 16 > 0

Vậy phương trình luôn có hai nghiệm phân biệt x₁ và x₂.

Áp dụng định lí Vi – et, ta có:

$\left\{\begin{array}{l}{x}_1+x_2=m\\ x_1{x}_2=-4\end{array}\right.$

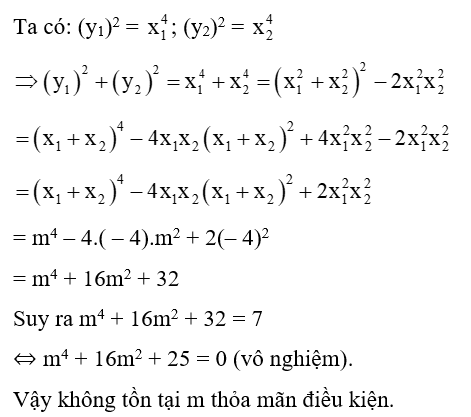
Câu 20: Cho hàm số bậc nhất y = mx - 4. Tìm m trong các trường hợp sau

a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm hoành độ bằng 2.

b) Đồ thị cắt đường y = -3x + 2 tạiđiểm có tung độ bằng 5.

Lời giải:

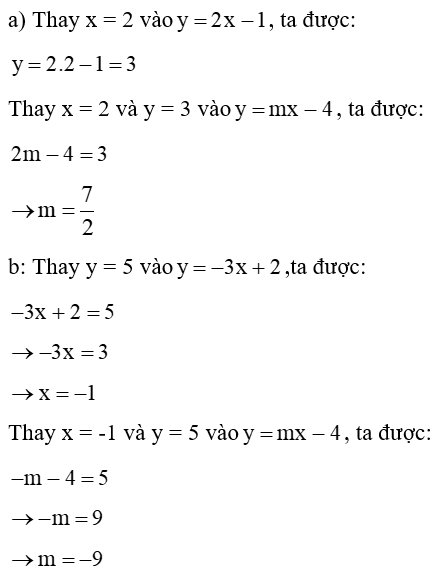
Câu 21: Chứng minh đẳng thức sau:

$\frac{1+si{n}^{2}x}{1-si{n}^{2}x}=1+2ta{n}^{2}x$

Lời giải:

Có ${\sin }^{2}x+{\cos }^{2}x=1\Rightarrow 2{\sin }^{2}x=1-{\cos }^{2}x+{\sin }^{2}x$

$\Rightarrow 1+{\sin }^{2}x=2{\sin }^{2}x+{\cos }^{2}x$

$\Rightarrow VT=\frac{2{\sin }^{2}x+{\cos }^{2}x}{{\cos }^{2}x}=2{\tan }^{2}x+1$.

Câu 22: Biết chu vi của một hình chữ nhật gấp 6 lần chiều rộng. Hỏi chiều dài gấp mấy lần chiều rộng?

Lời giải:

Chu vi bằng tổng chiều dài cộng chiều rộng và chu vi gấp 6 lần chiều rộng nên chiều dài gấp 5 lần chiều rộng.

Câu 23: Phân tích đa thức sau thành nhân tử:  x² – 2x – 4y² – 4y.

Lời giải:
x² – 2x – 4y² – 4y = x² – 4y² – 2x – 4y

= (x² – 4y²) – (2x + 4y)

= (x – 2y)(x + 2y) – 2(x + 2y)

= (x + 2y)(x – 2y – 2).

Câu 24: Một lớp học có 25 học sinh học khá các môn tự nhiên, 24 học sinh học khá các môn xã hội, 10 học sinh học khá cả môn tự nhiên lẫn môn xã hội, đặc biệt vẫn còn 3 học sinh chưa học khá cả hai nhóm môn ấy. Hỏi lớp có bao nhiêu học sinh chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội).

A. 39;

B. 26;

C. 29;

D. 36.

Lời giải:

Đáp án đúng là: A

Số học sinh trong lớp chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội) là:

25 + 24 – 10 = 39 (học sinh)

Vậy lớp có 39 học sinh chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội).

Câu 25: Phát biểu nào sau đây đúng?

A. Tổng của hai vectơ khác $\overrightarrow{0}$  là một vectơ khác $\overrightarrow{0}$ .

B. Hai vectơ cùng phương với một vectơ khác $\overrightarrow{0}$  vectơ thì hai vectơ đó cùng phương với nhau.

C. Hiệu của hai vectơ có độ dài bằng nhau là $\overrightarrow{0}$ .

D. Hai vectơ không bằng nhau thì có độ dài không bằng nhau.

Lời giải:

Hai vectơ cùng phương với một vectơ khác $\overrightarrow{0}$  thì giá của chúng song song hoặc trùng nhau nên hai vectơ này cùng phương với nhau.

Câu 26: Tổng các góc của hình thang cân là bao nhiêu?

A. 180°;

B. 360°;

C. 90°;

D. 720°.

Lời giải:

Đáp án đúng là: B.

Tổng các góc của một hình thang cân là 360°.

Câu 27: Chứng minh tích của 4 số tự nhiên liên tiếp chia hết cho 24.

Lời giải:
Gọi 4 số tự nhiên liên tiếp là x; x + 1; x + 2; x + 3.

Ta có tích 4 số đó là x(x + 1)(x + 2)(x + 3).

• Vì x(x + 1) là tích 2 số liên tiếp nên chia hết cho 2;

• Vì x(x+1)(x+2) là tích 3 số liên tiếp nên chia hết cho 3;

• Vì x(x+1)(x+2)(x+3) là tích 4 số liên tiếp nên chia hết cho 4.

Mà 2 . 3 . 4 = 24 ⇒ x(x + 1)(x + 2)(x + 3) là bội của 24

Hay x(x + 1)(x + 2)(x + 3) chia hết cho 24.

Câu 28: Định lý talet trong tam giác.

Lời giải:

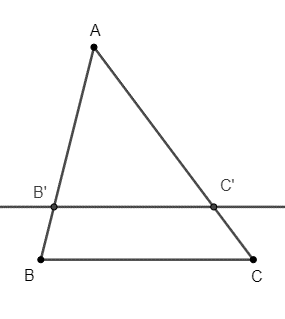
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

Câu 29: Cho hàm số bậc nhất y = (2m – 1)x + m – 1 (d). Tìm m để khoảng cách từ O(0; 0) đến (d) là $\sqrt{3}$ .

Lời giải:

Ta có y = (2m – 1)x + m – 1 (d).

Điều kiện 2m – 1 ≠ 0 $m\ne \frac{1}{2}$ .

Gọi A là giao điểm của (d) và Ox $\Rightarrow A\left(\frac{-m+1}{2m-1};0\right)$ .

Gọi B là giao điểm của (d) và Oy nên B(0; m – 1).

Gọi H là chân đường cao kẻ từ O xuống (d).

Để khoảng cách từ O đến (d) bằng $\sqrt{3}$  thì $OH=\sqrt{3}$ .

Khi đó $OA=\left|\frac{-m+1}{2m-1}\right|$ ; OB = |m – 1|.

Xét $\Delta$ OAB vuông tại O, đường cao AH có:

$\frac{1}{O{H}^2}=\frac{1}{O{A}^2}+\frac{1}{O{B}^2}$

$\iff \frac{1}{3}=\frac{1}{{\left(\frac{-m+1}{2m-1}\right)}^2}+\frac{1}{{\left(m-1\right)}^2}$ (điều kiện: m ≠ 1).

$$\begin{gathered} \iff \frac{1}{3}=\frac{{\left(2m-1\right)}^2}{{\left(m-1\right)}^2}+\frac{1}{{\left(m-1\right)}^2} \\ \iff \frac{1}{3}=\frac{4m^2-4m+1+1}{m^2-2m+1} \end{gathered}$$

⇔ m² – 2m + 1 = 12m² – 12m + 6

⇔ 11m² – 10m + 5 = 0

⇔$11\left(m^2-2\frac{5}{11}m+\frac{25}{121}\right)=\frac{30}{11}=0$

$\iff 11{\left(m-\frac{5}{11}\right)}^2+\frac{30}{11}=0$ (vô nghiệm).

Vậy không có giá trị nào của m thỏa mãn khoảng cách từ O đến (d) bằng $\sqrt{3}$ .

Câu 30: Tìm x biết:

$\frac{1}{3}x+\frac{2}{5}\left(x+1\right)=0$.

Lời giải:

Câu 31: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình 16^x – m4^x+1 + 5m² – 45 = 0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?

A. 13;

B. 3;

C. 6;

D. 4.

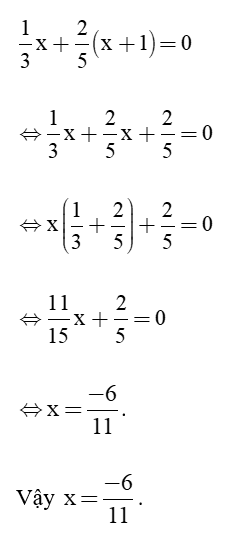
Lời giải:

Đáp án đúng là: B

Đặt t = 4^x (t > 0). Phương trình đã cho trở thành

t² – 4mt + 5m² – 45 = 0 (*)

Với mỗi nghiệm t > 0 của phương trình (*) sẽ tương ứng với duy nhất một nghiệm x của phương trình ban đầu. Do đó, yêu cầu bài toán tương đương phương trình (*) có hai nghiệm dương phân biệt.

Khi đó: $\left\{\begin{array}{l}\Delta \text{'}>0\\ S>0\\ P>0\end{array}\right.\iff \left\{\begin{array}{l}-m^2+45>0\\ 4m>0\\ 5m^2-45>0\end{array}\right.$

$\iff \left\{\begin{array}{l}-3\sqrt{5}<m<3\sqrt{5}\\ m>0\\ \left[\begin{array}{l}m<-3\\ m>3\end{array}\right.\end{array}\right.\iff 3<m<3\sqrt{5}$

Do m ∈ ℤ nên m ∈ {4; 5; 6}.

Vậy S = 4 + 5 + 6 = 15.

Câu 32: Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{x^3}{3}+2x^2+3x-4$  trên [−4; 0] lần lượt M và m. Giá trị của M + m bằng:

Lời giải:

Đáp án đúng là: B

Hàm số $y=\frac{x^3}{3}+2x^2+3x-4$ xác định và liên tục trên [−4; 0].

y’ = x² + 4x + 3, y’ = 0 $\iff \left[\begin{array}{l}x=-1\\ x=-3\end{array}\right.$

Ta có: f(0) = −4; f(−1) $=\frac{-16}{3}$ ; f(−3) = −4; $f(-4)=\frac{-16}{3}$ .

Vậy M = −4, $m=\frac{-16}{3}$  nên $M+n=-\frac{28}{3}$ .

Câu 33: Rút gọn biểu thức: 3x(x – 2) – 5x(1 – x) – 5(x² – 3).

Lời giải:

3x(x – 2) – 5x(1 – x) – 5(x² – 3)

= 3x² – 6x – 5x + 5x² – 5x² + 15

= 3x² – 11x + 15.

Câu 34: Phân tích đa thức x² – 2x – 15.

Lời giải:

Ta có: x² – 2x – 15 = x² – 5x + 3x – 15

= (x² + 3x) – (5x + 15) = x(x + 3) – 5(x + 3)

= (x + 3)(x – 5).

Câu 35: Cho hai số a, b thỏa mãn điều kiện a + b = 1.

Chứng minh a³ + b³ + ab $\ge \frac{1}{2}$ .

Lời giải:

Ta có: a³ + b³ + ab = (a + b)³ – 3ab(a + b) + ab

= 1 – 3ab + ab (do a + b = 1)

= 1 – 2ab = 1 – 2a( 1 – a)

= 2a² – 2a + 1 = $2\left(a^2-a+\frac{1}{4}\right)+\frac{1}{2}$

$=2{\left(a-\frac{1}{2}\right)}^2+\frac{1}{2}\ge \frac{1}{2}$.

Vậy $a^3+b^3+ab\ge \frac{1}{2}$  (đpcm).

Câu 36: Người ta muốn xây một cái bể chứa nước dạng khối hộp chữ nhật không nắp có thể tích $\frac{500}{3}$ m³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/m³. Nếu biết xác định kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất, chi phí thấp nhất đó là:

A. 70 triệu đồng;

B. 85 triệu đồng;

C. 80 triệu đồng;

D. 75 triệu đồng.

Lời giải:

Đáp án đúng là: D

Gọi các yếu tố như hình vẽ, diện tích phần phải xây của bể là phần xung quanh và đáy.

$\left\{\begin{array}{l}V=2x^3.h=\frac{500}{3}\\ S=2x^2+6xh\end{array}\right.$

$\Rightarrow S=2x^2+\frac{500}{x}=2x^2+\frac{250}{x}+\frac{250}{x}$

Áp dụng bất đẳng thức Cô-si ta có:

S ≥ $3.\sqrt[3]{2x^2.\frac{250}{x}.\frac{250}{x}}=3.50=150$

Vậy số chi phí thấp nhất là: 150 . 500 000 = 75 000 000 (đồng).

Câu 37: Một liên đoàn bóng rổ có 10 đội, mỗi đội đấu với mỗi đội khác 2 lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là bao nhiêu?

A. 45;

B. 90;

C. 100;

D. 180.

Lời giải:

Đáp án đúng là: B.

Cứ hai đội nếu đá cả lượt đi và lượt về thì có 2 trận đấu diễn ra.

Vậy có tất cả: $2.C_{10}^2=90$  (trận).

Câu 38: Tìm giá trị lớn nhất của biểu thức $A=11-\sqrt{x^2+7x+4}$ .

Lời giải:

Ta có: $A=11-\sqrt{{\left(x+\frac{7}{2}\right)}^2-\frac{25}{4}}\le 11$ ( do $\sqrt{{\left(x+\frac{7}{2}\right)}^2-\frac{25}{4}}\ge 0$ )

Đẳng thức xảy ra khi ${\left(x+\frac{7}{2}\right)}^2=\frac{25}{4}\iff \left[\begin{array}{l}x=-1\\ x=-6\end{array}\right.$

Vậy A_max = 11.

Câu 39: Cho các vecto $\overrightarrow{a};\overrightarrow{b}\ne 0$ . Khẳng định nào sau đây đúng?

Lời giải:

Đáp án đúng là: D.

Vậy D là đáp án đúng.

Câu 40: Chứng minh n³ – n chia hết cho 3 với mọi số nguyên n.

Lời giải:

Ta có n³ – n = n(n² – 1) = n(n + 1)(n – 1)

Vì n(n + 1)(n – 1) là tích ba số nguyên liên tiếp nên $n(n+1)(n-1)⋮3$ .

Vậy $(n^3-n)⋮3$  (đpcm).

Câu 41: Tìm x biết: (x – 5)(x – 4) – (x + 1)(x – 2) = 7.

Lời giải:

(x – 5)(x – 4) – (x + 1)(x – 2) = 7

⇔ x² – 9x + 20 – (x² – x – 2) = 7

⇔ −8x + 22 = 7

⇔ 8x = 15

$\iff x=\frac{15}{8}$

Vậy $x=\frac{15}{8}$ .

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 11)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 12)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 13)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 14)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 15)