1500 câu hỏi ôn tập môn Toán có đáp án (Phần 79)

1500 câu hỏi ôn tập Toán (Phần 79)

Câu 1: Một chiếc đồng hồ đánh chuông, số tiếng chuông được đánh đúng bằng số mà kim giờ chỉ tại thời điểm đánh chuông. Hỏi một ngày đêm đồng hồ đó đánh bao nhiêu tiếng chuông?

Lời giải:

Trong một ngày đêm kim giờ quay hai vòng

Vậy trong một ngày đêm đồng hồ đó đánh 

(1 + 2 + ... + 12) . 2 = 12 . (12 + 1) = 156 tiếng.

Câu 2: Hình chiếu vuông góc là hình biểu diễn thu được từ phép chiếu nào?

Lời giải:

Hình chiếu vuông góc là hình biểu diễn thu được từ phép chiếu song song.

Câu 3: Hai góc cùng phụ một góc là như thế nào?

Lời giải:

Hai góc cùng phụ một góc có nghĩa là hai góc đấy lần lượt cộng với một góc ra 90°.

Và hai góc cùng phụ một góc là hai góc bằng nhau, vì cùng cộng với một góc ra 90°.

Câu 4: Tìm ƯCLN (16; 40; 176).

Lời giải:

Ta có:

16 = 2⁴

40 = 2³ . 5

176 = 2⁴ . 11

ƯCLN (16; 40; 176) = 2³ = 8.

Câu 5: Chứng minh nếu n² là số chẵn thì n cũng là số chẵn.

Lời giải:

Giả sử n² là số chẵn nhưng n là số lẻ

⇒ n có dạng 2k + 1

⇒ n² = (2k+1)² = 4k² + 4k + 1 là số lẻ (mâu thuẫn đề bài)

⇒ Giả sử trên sai.

Vậy nếu n² là số chẵn thì n cũng là số chẵn.

Câu 6: Theo kế hoạch hai tổ được giao sản xuất 600 sản phẩm trong một thời gian đã định. Do cải tiến kĩ thuật nên tổ I đã sản xuất vượt mức kế hoạch 18% và tổ II sản xuất vượt mức kế hoạch 21%. Vì vậy trong cùng thời gian quy định hai tổ đã hoàn thành vượt mức 120 sản phẩm. Tính số sản phẩm được giao của mỗi tổ theo kế hoạch.

Lời giải:

Gọi số sản phẩm tổ I và tổ II được giao theo ké hoạch lần lượt là:

x, y (x, y ∈ ℕ^*; x, y < 600)

Vì theo kế hoạch hai tổ được giao sản xuất 600 sản phẩm nên ta có:

x + y = 600  (1)

Vì tổ I đã sản xuất vượt mức kế hoạch 18% nên số sản phẩm vượt mức của tổ I là: 0,18x

Vì tổ II đã sản xuất vượt mức kế hoạch 21% nên số sản phẩm vượt mức của tổ II là: 0,21y

Vì 2 tổ vượt mức 120 sản phẩm nên ta có phương trình:

0,18x + 0,21y = 120 (2)

Từ (1) và (2) ta có hệ: $\left\{\begin{array}{l}x+y=600\\ \mathrm{0,18}x+\mathrm{0,21}y=120\end{array}\right.$  ⇔ $\left\{\begin{array}{l}x=200\\ y=400\end{array}\right.$

Vậy số sản phẩm được giao của tổ I, II theo kế hoạch lần lượt là 200 sản phẩm và 400 sản phẩm.

Câu 7: Tính giá trị biểu thức: 36.55 – 185.11 + 121.5.

Lời giải:

36 . 55 – 185 . 11 + 121 . 5

 = 1980 – 2035 + 605

 = (– 55) + 605

 = 550

Câu 8: Tính giá trị của biểu thức A = x² – 6xy + 9y² – 15 tại x = 37, y = – 1.

Lời giải:

A = x² – 6xy + 9y² – 15

A = 37² – 6.37.(-1) + 9.(-1)² – 15

A = 1369 + 222 + 9 – 15

A = 1585

Vậy với x = 37, y = – 1 thì A = 1585.

Câu 9: Tìm giá trị nhỏ nhất của A = a² – 4ab + 5b² + 10a – 22b + 28.

Lời giải:

A = a² – 4ab + 5b² + 10a – 22b + 28

A = (a² – 4ab + 4b²) + b² – 2b + 1 + 10a – 22b + 27

A = (a – 2b)² + (b – 1)² + 10(a – 2b) + 27

A = (a – 2b + 5)² + (b – 1)² + 2

Vì (a – 2b + 5)² + (b – 1)² ≥ 0 nên A ≥ 2

Vậy giá trị nhỏ nhất của A là 2 khi:

$\left\{\begin{array}{l}a-2b+5=0\\ b-1=0\end{array}\right.$ hay $\left\{\begin{array}{l}a=-3\\ b=1\end{array}\right.$ .

Câu 10: Nhân ngày 20/10 cửa hàng bán túi sách và ví da  giảm 30% cho tất cả sản phẩm ai có thẻ VIP giảm 10% trên giá đã giảm.

a) Mẹ bạn An có thẻ VIP thì khi mua 1 cái tui trị giá 500000 đồng phải trả bao nhiêu ?

b) Mẹ bạn An mua thêm 1 cái ví nên phải trả là 693000 đồng. Vậy giá bán đầu của cái bóp là bao nhiêu?

Lời giải:

a) Số tiền phải trả khi giảm 30% cho túi xách là:

500000 – 500000.30% = 350000 (đồng)

Số tiền phải trả khi giảm tiếp 10% là:

350000 – 350000.10% = 315000 (đồng)

Vậy khi mua 1 túi xách giá 500000đ thì mẹ An phải trả 315000 đồng

b) Gọi x (đồng) là giá ban đầu của cái bóp (x > 0)

Số tiền phải trả cho cái bóp là:

693000 – 315000 = 378000 (đồng)

Số tiền phải trả cho cái bóp sau lần giảm 30% là:

x – 30%.x = 0,7x (đồng)

Số tiền phải trả cho cái bóp khi giảm tiếp 10% là:

0,7x – 10%.0,7x = 0.63x (đồng)

Theo đề bài ta có pt:

0,63x = 378000

⇔ x = 600000 (nhận)

Vậy giá ban đầu của cái bóp là 600000 đồng.

Câu 11:  Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?

Lời giải:

Gọi số xe loại A cần thuê là: x (chiếc) (x ∈ ℕ);

Số xe loại B cần thuê là: y (chiếc) (y ∈ ℕ)

Xe loại A có 9 chiếc, xe loại B có 8 chiếc 

⇒ 0 ≤ x ≤ 9; 0 ≤ y ≤ 8 (1)

Chi phí cần để thuê xe là: T = 4x + 3y (triệu đồng)

Xe loại A có thể chở tối đa 20 người, xe loại B có thể chở tối đa 10 người, mà số người công ty cần chở là 120 người

⇒ Tổng số người cả hai loại xe có thể chở tối thiểu là 120 người

⇒ 20x + 10y ≥ 120 ⇒ 2x + y ≥ 12  (2)

Xe loại A có thể chở tối đa 0,5 tấn hàng, xe loại B có thể chở tối đa 2 tấn hàng, mà số tấn hàng công ty cần chở là 6,5 tấn

⇒ Tổng số tấn hàng cả hai loại xe có thể chở tối thiểu là 6,5 tấn hàng 

⇒ 0,5x + 2y ≥ 6,5 ⇒ x + 4y ≥ 13 (3)

Từ (1); (2)và (3) ta có hệ bất phương trình: 

$\left\{\begin{array}{l}0\le x\le 9\\ 0\le y\le 8\\ 2x+y\ge 12\\ x+4y\ge 13\end{array}\right.$

Miền nghiệm của hệ là tứ giác ABCD với:

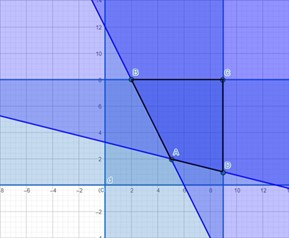A(5; 2) là giao của 2 đường thẳng 2x + y = 12 và x + 4y = 13

B(2; 8) là giao của 2 đường thẳng 2x + y = 12 và y = 8

C(9; 8) là giao của 2 đường thẳng x = 9 và y = 8

D(9; 1) là giao của 2 đường thẳng x = 9 và x + 4y = 13

Tại A(5; 2) thì T = 4.5 + 3.2 = 26 (triệu đồng)

Tại B(2; 8) thì T = 4.2 + 3.8 = 32 (triệu đồng)

Tại C(9; 8) thì T = 4.9 + 3.8 = 60 (triệu đồng)

Tại D(9; 1) thì T = 4.9 + 3.1 = 39 (triệu đồng)

⇒ Chi phí nhỏ nhất là T_min = 26 (triệu đồng)

⇒ Phải thuê 5 chiếc xe loại A và 2 chiếc xe loại B để chi phí bỏ ra là thấp nhất.

Câu 12: Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần?

Lời giải:

Chọn 9 số từ 10 chữ số {0;1;2;3;...9} có $C_{10}^9$ cách

Sắp xếp 9 chữ số đó theo thứ tự giảm dần có 1 cách

Vậy số số tự nhiên có 9 chữ số mà các chữ số của nó được sắp xếp theo thứ tự giảm dần là: $C_{10}^9$ .1 = 10 số.

Câu 13: Trong mặt phẳng Oxy, cho đường thẳng d: 2x – 5y + 3 = 0. Viết phương trình đường thẳng sao cho d là ảnh của đường thẳng ∆ qua phép quay tâm I(– 1; 2), góc quay – 180°.

Lời giải:

Q_(I;−180º): Δ ⇒ d

Phép quay −180° là phép đối xứng tâm nên Δ và d song song hoặc trùng với nhau 

Đặt Δ: 2x − 5y + c = 0

Chọn điểm N(1;1) ∈ d, tạo ảnh của N là điểm M ∈ Δ

I là trung điểm MN nên:

M(2.(−1)−1;2.2−1) = (−3; 3)

M ∈ Δ nên ta có:

−2.3 − 5.3 + c = 0

⇒ c = 21

Vậy Δ: 2x − 5y + 21 = 0.

Câu 14: Cô chia kẹo, bánh cho các cháu. Số lượng bánh bằng số lượng kẹo. Nếu chia mỗi cháu 3 bánh thì thừa 2 bánh. Nếu chia mỗi cháu 5 kẹo thì thiếu 28 cái. Tính số kẹo, số bánh và số cháu được chia?

Lời giải:

Vì số lượng kẹo bằng số lượng bánh nên chia kẹo cũng như chia bánh.

1 cháu 3 bánh thì thừa 2 bánh

1 cháu 5 bánh thì thiếu 28 bánh

Ta có sơ đồ:

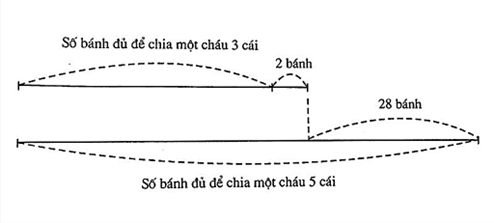
Số bánh dủ chia cho 1 cháu 5 cái nhiều hơn số bánh dủ chia cho 1 cháu 3 cái là:
2 + 28 = 30 (cái)
1 cháu dược chia 5 cái nhiều hơn 1 cháu dược chia 3 cái là ;
5 – 3 =  2(cái )
Số cháu được chia bánh là:
30 : 2 = 15 (cháu)
Số bánh (hay số kẹo) là;
3 . 15 + 2 = 47 (cái).

Câu 15: Tìm x biết x + 17 chia hết cho x + 11.

Lời giải:

Ta có: x + 17 = x + 11 + 6

Vì (x + 11) chia hết cho x + 11 nên để x + 17 chia hết cho x + 11 thì 6 chia hết cho (x + 11)

Hay x + 11 ∈ Ư(6)

Suy ra: x + 11 ∈ {– 6; 6; – 2; 2; 3; – 3; 1; – 1}

Hay x ∈ {– 17; – 5; – 13; – 9; – 8; – 14; – 10; – 12}.

Câu 16: Cách bấm dấu >, <, lớn hơn hoặc bằng bé hơn hoặc bằng trên máy tính casio 580VNX.

Lời giải:

Bấm MODE, sau đó chọn phần kiểm tra đúng/ sai sau đó ấn nút OPTN.

Câu 17: Một người mua 72,8 kg gạo nếp và gạo tẻ. Biết rằng số gạo nếp bằng $\frac{3}{5}$  số gạo tẻ. Hỏi người đó mua bao nhiêu ki - lô - gam gạo mỗi loại?

Lời giải:

Tổng số phần bằng nhau là:

 3 + 5 = 8 (phần)

Người đó mua số kg gạo nếp là:

 72,8 : 8 . 3 = 27,3(kg)

Người đó mua số kg gạo tẻ là:

 72,8 − 27,3 = 45,5(kg).

Câu 18: Hai tấm vải dài 124m. Hỏi mỗi tấm vải dài bao nhiêu mét? Biết rằng tấm vải thứ nhất dài hơn tấm vải thứ hai 18m.

Lời giải:

Tấm vải thứ nhất dài số mét là :

(124 + 18) : 2 = 71 (m)

Tấm vải thứ hai dài số mét là :

124 – 71 = 53 (m)

Đáp số: Tấm vải thứ nhất: 71m

Tấm vải thứ hai: 53m.

Câu 19: Trong 1 cái lọ chứa n cái kẹo (n ∈ ℕ^*). 2 bạn Lan và Khoa chơi một trò chơi như sau: 2 người luân phiên lấy kẹo từ trong lọ ra, mỗi lần đc lấy 1, 2, 3, 4, 5 cái. Người lấy được cái kẹo cuối cùng trong lọ là người chiến thắng. Nếu Lan đi trước:

a) Với n = 10, hãy chỉ ra cách chơi của Lan để Lan là người thắng.

b) Với n = 74, hãy chỉ ra cách chơi của Lan để Lan là người thắng.

Lời giải:

a) Để Lan bốc được cái kẹo cuối cùng thì số kẹo còn lại trong lượt cuối Nam bốc phải bằng 6 để số kẹo còn lại sau khi Nam bốc luôn nằm trong khả năng bốc của Lan.

Nam lấy 1 - Lan lấy 5

Nam lấy 2 - Lan lấy 4

Nam lấy 3 - Lan lấy 3

Nam lấy 4 - Lan lấy 2

Nam lấy 5 - Lan lấy 1

Số kẹo Lan bốc trong lượt đầu là: 10 – 6 = 4 (cái)

Vậy Lan phải bốc 4 cái kẹo lượt đầu.

b) Để Lan thắng thì số kẹo còn lại trước lượt Nam bốc luôn phải là bội của 6 để số kẹo còn lại trong lượt cuối Nam bốc có thể chắc chắn bằng 6

Bội của 6 gần 74 là 72

Vậy Lan cần bốc 74 – 72 = 2 viên trong lượt đầu và các lần bốc tiếp theo số kẹo bốc sao cho số kẹo còn lại trước lượt Nam bốc luôn phải là bội của 6.

Câu 20: Có ba chiếc hộp mỗi hộp đựng 2 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 1 viên bi xanh?

Lời giải:

Gọi Ω là không gian mẫu của phép thử.

Số cách lấy mỗi hộp một viên bi: 10.10.10 = 1000(cách).

Suy ra, số phần tử của Ω là: n(Ω) = 1000 (cách)

Gọi A là biến cố: “Trong 3 viên bi lấy được có ít nhất 1 viên bi xanh”

Suy ra là biến cố: “Trong 3 viên bi lấy được không có viên bi xanh”

Số cách lấy mỗi hộp một viên bi sao cho không có bi xanh: 8.8.8 = 512 (cách).

Suy ra: $n\left(\overline{A}\right)$  = 512 (cách)

Xác suất cần tìm là: P(A) = 1 – $P\left(\overline{A}\right)=1-\frac{512}{1000}=\frac{488}{1000}$ .

Câu 21: Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?

Lời giải:

Khách hàng phải gửi số tiền là:

780000 : 0,65 . 100 = 12000000 (đồng)

Đáp số: 12000000 (đồng).

Câu 22: Cho dãy số (u_n) với u_n = 2n + 3. Dãy số này có phải cấp số cộng không?

Lời giải:

Ta có: u_n+1 = 2(n + 1) + 3 = 2n + 5

Xét u_n+1 – u_n = 2n + 5 – (2n + 3) = 2

Vậy u_n là cấp số cộng với công sai d = 2.

Câu 23: Cho hai tập hợp A = [m – 4; 1], B = (–3; m]. Tính tổng tất cả các giá trị nguyên của m để A ∪ B = B.

Lời giải:

Để A ∪ B = B thì

–3 < m – 4 ≤ 1 ≤ m

⇔ $\left\{\begin{array}{l}m-4>-3\\ m\ge 1\\ m-4\le 1\end{array}\right.$ ⇔ $\left\{\begin{array}{l}m>1\\ m\ge 1\\ m\le 5\end{array}\right.$  ⇔  1 < m ≤ 5

Vậy m ∈ {2; 3; 4; 5}.

Tổng các giá trị nguyên của m là: 2 + 3 + 4 + 5 = 14.

Câu 24: Cho hình chữ nhật ABCD có AB bằng 6 cm BC = 4 cm quay hình chữ nhật đó quanh AB. Diện tích xung quanh và diện tích toàn phần của hình trụ là S₁, S₂. Tính S₁, S₂?

Lời giải:

 Quay hình chữ nhật ABCD quanh AB thì được 1 hình trụ có:

+ Chiều cao bằng AB = 6cm

+ Đáy là đường tròn có bán kính r = BC = 4cm

S₁ = 2π.AB.BC = 2.3,14.6.4 = 150, 72 (cm²)

S₂ = 2πr² +2πrh = 2.3,14.4² + 2.3,14.4.6 = 251,2 (cm²).

Câu 25: Một đàn gà có 16 con gà trống và 34 con gà mái. Tỉ số phần trăm của số gà trống và số gà của đàn?

Lời giải:

Cả đàn có số con gà là:

16 + 34 = 50 (con)

Tỉ số phần trăm của số gà trống và số gà của đàn là:

16 : 50 = 0,32 = 32%.

Câu 26: Nếu một túi hạt giống cỏ gieo vừa đủ trên 25m² đất, thì cần bao nhiêu túi hạt giống để gieo hết bãi cỏ?

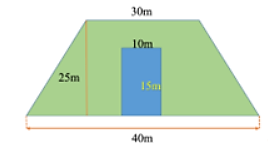
Lời giải:

Tổng diện tích khu đất đó là:

$\frac{\left(30+40\right).25}{2}=875\left(m^2\right)$

Diện tích ngôi nhà là:

15 . 10 = 150 (m²)

Diện tích bãi cỏ là:

875 – 150 = 725 (m²)

 Số túi hạt giống cần là:

725 : 25 = 29

Vậy số túi cần là: 29.

Câu 27: Giá hoa tháng năm tăng 10 % so với giá hoa tháng bốn. Giá hoa tháng sáu tăng 10 % so với giá hoa tháng năm hỏi giá hoa tháng sáu tăng bao nhiêu phần trăm so với sáu tháng bốn?

Lời giải:

Coi giá hoa tháng 4 là 100100 % thì giá hoa tháng 5 là:

100% + 10% = 110% = 1,1

Giá hoa tháng sáu so với giá hoa tháng 4 chiếm số phần trăm là:

1,1 + 1,1 : 100 . 10 = 1,21 = 121 %

Vậy giá hoa tháng sáu tăng số phần trăm so với giá hoa tháng bốn là:

121% − 100 % = 21 %

Vậy giá hoa tháng sáu tăng 21 % so với giá hoa tháng bốn.

Câu 28: Tìm hai số biết hiệu giữa hai số là 18 và số lớn gấp 7 lần số bé.

Lời giải:

Gọi số lớn là a, số bé là b

Ta có: a – b = 18 (1)

a = 7b (2)

Thế (2) vào (1), khi đó ta có:

7b – b = 18

⇔ 6b = 18

⇔ b = 3

⇒ a = 3.7 = 21

Vậy số lớn là 21, số bé là 3.

Câu 29: Tìm x biết: x – 7,02 = 19 : 3,8.

Lời giải:

x – 7,02 = 19 : 3,8

⇔ x – 7,02 = 5

⇔ x = 5 + 7,02

⇔ x = 12,02

Vậy x = 12,02.

Câu 30: Một nhà sản xuất quyết định giảm giá 8% cho một dòng máy tính bảng hỏi giá của máy tính bảng sau khi giảm giá là bao nhiêu biết rằng giá gốc của máy tính là 5 triệu đồng.

Lời giải:

Số tiền được giảm giá của máy tính là:

5000000 . 8% = 400000 (đồng)

Giá của máy tính sau khi giảm giá là:

5000000 – 400000 = 4600000 (đồng)

Câu 31: Có bao nhiêu giá trị của x thỏa mãn 60 < x < 95 và x vừa chia hết cho 5, vừa chia hết cho 3.

Lời giải:

Ta có: x chia hết cho 5 thì x có tận cùng là 0 hoặc 5

Suy ra: x = 65; 70; 75; 80; 85; 90

Trong 6 số nêu trên, có 75 và 90 chia hết cho 3

Vậy có 2 giá trị của x thỏa mãn yêu cầu bài toán.

Câu 32: Hai số có tổng bằng 126 và thương của chúng là 2. Tìm số lớn, số bé?

Lời giải:

Do thương của hai số là 2, nên ta coi số lớn là 2 phần, thì số nhỏ là 1 phần.

Tổng số phần bằng nhau là:

2 + 1 = 3 (phần)

Số nhỏ là:

126 : 3 = 42

Số lớn là:

42 . 2 = 84

Vậy số lớn là 84, số bé là 42.

Câu 33: Tính hiệu của 274 với tích của 17 và 5.

Lời giải:

Ta có: 274 – 17.5 = 274 – 85 = 189

Vậy hiệu của 274 với tích của 17 và 5 là 189.

Câu 34: Tuổi của Đức 4 năm trước đây bằng một nửa tuổi của Đức 5 năm sau này. Tính tuổi Đức hiện nay?

Lời giải:

Gọi tuổi Đức hiện nay là x

Tuổi của Đức 4 năm trước là x – 4

Tuổi của Đức 5 năm sau là x + 5

Ta có: x + 5 = 2(x – 4)

⇔ x + 5 = 2x – 8

⇔ 13 = x

Vậy tuổi của Đức hiện nay là 13 tuổi.

Câu 35: Bác Ba cần lát gạch cho một nền nhà hình chữ nhật có chiều dài là 20m và chiều rộng bằng một phần tư chiều dài. Bác Ba muốn lót gạch hình vuông cạnh 4dm lên nền nhà đó nên đã mua gạch bông với giá một viên gạch là 80000 dồng. Hỏi số tiền mà bác Ba phải trả để mua gạch?

Lời giải:

Chiều rộng của nền nhà là: 20 : 4 = 5 (m)

Diện tích của nền nhà là : 20 . 5 =100 (m²)

Diện tích của một viên gạch là: 0,4 . 0,4 = 0,16(m²)

Số viên gạch cần lót là: 100 : 0,16 = 625 (viên)

Số tiền bác Ba phải trả để mua gạch là: 625 . 80000 = 50000000 (đồng).

Câu 36: Cho 2 đa thức A(x) = 2x³ – x² – x + 1 và B(x) = x – 2.

a) Tìm thương và số dư của phép chia đa thức A(x) cho đa thức B(x).

b) Tìm số nguyên x để A(x) chia hết cho B(x).

Lời giải:

a) A(x) = 2x³ – x² – x + 1 = (2x³ – 4x²) + (3x² – 6x) + (5x – 10) + 11

= (x – 2)(2x² + 3x + 5) + 11

Suy ra: A(x) chia B(x) được thương là 2x² + 3x + 5 và số dư là 11

b) Để A(x) chia hết cho B(x) thì 11 ⋮ B(x)

Tức 11  ⋮  (x – 2)

Hay x – 2 ∈ Ư(11) = {11; 1; –1; –11}

Suy ra: x ∈ {13; 3; 2; –9}.

Câu 37: Một con cá có đuôi nặng 250 g, đầu nặng bằng đuôi và nửa thân, thân nặng bằng đầu và đuôi. Hỏi con cá nặng bao nhiêu ki – lô – gam ?

Lời giải:

Gọi đầu là a, thân là b, đuôi là c

Ta có: b = a + c = a + 250 (1)

a = c + 0,5b = 250 + 0,5b (2)

Thế (2) vào (1) ta có:

b = 250 + 0,5b + 250

⇔ 0,5b = 500

⇔ b = 500 : 0,5

⇔ b = 1000 (gam)

Vậy thân cá nặng 1000 (gam)

Đầu cá nặng là:

205 + 1000 : 2 = 750 (gam)

Con cá nặng là:

250 + 1000 + 750 = 2000 (gam) = 2 (kg)

Câu 38: Tính tổng các số tự nhiên liên tiếp từ 1200 đến 1360.

Lời giải:

Từ 1200 đến 1360 có số số hạng là:

(1360 − 1200) : 1 + 1 = 161 (số hạng)

Tổng các số tự nhiên liên tiếp từ 1200 đến 1360 là:

(1360 + 1200) . 161 : 2 = 206080.

Câu 39: Xếp ngẫu nhiên 3 quyển sách lý khác nhau, 2 quyển sách toán khác nhau và 4 quyển sách hóa khác nhau thành 1 hàng ngang trên kệ sách. Tính xác suất các sách cùng môn luôn đứng cạnh nhau.

Lời giải:

Số cách xếp 9 quyển sách lên thành 1 hàng là 9!

Suy ra: n(Ω) = 9!

Gọi A là biến cố “các sách cùng môn luôn đứng cạnh nhau”

Ta xếp các sách cùng 1 bộ môn thành 1 nhóm

Với 3 quyển sách Lý ta có: 3! cách xếp

Với 2 quyển sách Toán ta có: 2! cách xếp

Với 4 quyển sách Hóa ta có: 4! cách xếp

Ta hoán vị các nhóm sách cho nhau có 3! cách

Vậy n(A) = 3! . 2! . 3! . 4!

P(A) = $\frac{3!.2!.3!.4!}{9!}=\frac{1}{210}$ .

Câu 40: Số các số tự nhiên chẵn, có 4 chữ số khác nhau từng đôi một không tận cùng bằng 0 là?

Lời giải:

Gọi số có 4 chữ số khác nhau từng đôi một là $\overline{abcd}$

Do giả thiết là các số tự nhiên chẵn nên có 4 cách chọn d ∈{2;4;6;8}

Có 8 cách chọn a (a ≠ 0,a ≠ d)

Có 8 cách chọn b (b ≠ a,b ≠ d)

Có 7 cách chọn c (c ≠ a, c ≠ b, c ≠ d)

Vậy có 4.8.8.7 = 1792 số.

Câu 41: Nêu các ước của 2019.

Lời giải:

Vì 2019 = 1.2019 = 673.3 = (–673).(–3) = (–1).(–2019)

Ư(2019) = {±1; ±3; ±673; ±2019}.

Câu 42: Một cửa hàng có 28000l xăng. Tuần thứ nhất, cửa hàng bán được 48% số xăng đó. Số xăng trong tuần thứ nhất gấp đôi số xăng bán được tuần thứ hai. Hỏi sau 2 tuần, cửa hàng còn lại bao nhiêu lít xăng?

Lời giải:

Tuần thứ nhất bán được số lít xăng là:

28000 : 100 . 48 = 13440 (lít)

Tuần thứ hai bán được số lít xăng là:

13440 : 2 = 6720 (lít)

Cả 2 tuần bán được số lít xăng là:

13440 + 6720 = 20160 (lít)

Sau 2 tuần cửa hàng đó còn lại số lít xăng là:

28000 − 20160 = 7840 (lít)

Câu 43: Tìm x biết: x : 3,5 = 4,3 – 3,22.

Lời giải:

x : 3,5 = 4,3 – 3,22

⇔ x : 3,5 = 1,08

⇔ x = 1,08 . 3,5

⇔ x = 3,78

Vậy x = 3,78.

Câu 44: Cuối năm 2005, số dân của 1 xã là 7500 người. Nếu tỉ lệ tăng dân số hàng năm là 1,6% thì cuối năm 2006 xã đó có bao nhiêu người?

Lời giải:

Số dân tăng thêm hằng năm của xã đó là: 

7500 : 100 . 1,6 = 120 (người)

Hết năm 2006 xã đó có số người là:

7500 + 120 = 7620 (người) 

Câu 45: Một mảnh đất hình vuông có chu vi là 72 m. Tính diện tích mảnh đất đó?

Lời giải:

Cạnh mảnh đất hình vuông là:

72 : 4 = 18 (m)

Diện tích mảnh đất hình vuông là:

18 . 18 = 324 (m²)

Câu 46: Một khu vườn hình chữ nhật có diện tích là 300m², 2 cạnh tỉ lệ với 4 và 3. Tính chiều dài chiều rộng khu vườn.

Lời giải:

Gọi chiều dài là x chiều rộng là y

Ta có: Hai cạnh khu vườn tỉ lệ với 4 và 3 nên 4y = 3x

Mà xy = 300

Thay vào ta có: 4y = 3 . $\frac{300}{y}$

⇔ 4y² = 900

⇔ y² = 900 : 4 = 225

⇔ y = 15

Vậy chiều rộng là 15m

Chiều dài là: 300 : 15 = 20 (m).

Câu 47: Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.

Lời giải:

Xếp các học sinh cùng 1 khối ngồi gần nhau

– Khối 12 có 4 học sinh nên có 4! cách

– Khối 11 có 5 học sinh nên có 5! cách

– Khối 10 có 4 học sinh nên có 6! cách

Hoán vị vị trí học sinh của 3 khối có 3! cách

Áp dụng quy tắc nhân:

Số cách sắp xếp 15 học sinh thỏa mãn yêu cầu bài toán là:

4! . 5! . 6! . 3! = 12441600 (cách)

Câu 48: Trong các số 1, 3, 5, 7, số nào khác với số còn lại? Giải thích?

Lời giải:

Số 1 khác với các số còn lại vì: 3, 5, 7 đều là số nguyên tố.

1 không phải là số nguyên tố.          

Câu 49: Diện tích của mạnh đất hình chữ nhật là 2782 m². Nếu gấp chiều rộng lên hai lần và chiều dài lên ba lần thì diện tích mới là bao nhiêu?

Lời giải:

Nếu gấp chiều rộng lên 2 lần thì diên tích gấp lên 2 lần

Nếu gấp chiều dài lên 3 lần thì diện tích gấp lên 3 lần

Như vậy diện tích gấp lên số lần là: 2.3 = 6 (lần)

Diện tích mảnh đất mới là: 2782 . 6 = 16692 (m²).

Câu 50: Biết 48 lít dầu nặng 36 kg. Một can chứa dầu nặng 30 kg. Biết cân nặng của can khi rỗng là 1,5 kg, số lít dầu chứa trong can đó là ?

Lời giải:

1 lít dầu cân nặng là:

36 : 48 = 0,75 (kg)

Số dầu chứa trong can là:

(30 − 1,5) : 0,75 = 38 (lít)

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: