Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe

Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe

Đề bài: Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?

* Lời giải:

Gọi số xe loại A cần thuê là: x (chiếc) (x ∈ ℕ);

Số xe loại B cần thuê là: y (chiếc) (y ∈ ℕ)

Xe loại A có 9 chiếc, xe loại B có 8 chiếc

⇒ 0 ≤ x ≤ 9; 0 ≤ y ≤ 8 (1)

Chi phí cần để thuê xe là: T = 4x + 3y (triệu đồng)

Xe loại A có thể chở tối đa 20 người, xe loại B có thể chở tối đa 10 người, mà số người công ty cần chở là 120 người

⇒ Tổng số người cả hai loại xe có thể chở tối thiểu là 120 người

⇒ 20x + 10y ≥ 120 ⇒ 2x + y ≥ 12 (2)

Xe loại A có thể chở tối đa 0,5 tấn hàng, xe loại B có thể chở tối đa 2 tấn hàng, mà số tấn hàng công ty cần chở là 6,5 tấn

⇒ Tổng số tấn hàng cả hai loại xe có thể chở tối thiểu là 6,5 tấn hàng

⇒ 0,5x + 2y ≥ 6,5 ⇒ x + 4y ≥ 13 (3)

Từ (1); (2)và (3) ta có hệ bất phương trình:

$\left\{\begin{array}{l}0\le x\le 9\\ 0\le y\le 8\\ 2x+y\ge 12\\ x+4y\ge 13\end{array}\right.$

Miền nghiệm của hệ là tứ giác ABCD với:

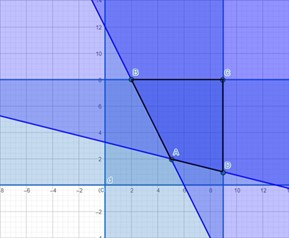A(5; 2) là giao của 2 đường thẳng 2x + y = 12 và x + 4y = 13

B(2; 8) là giao của 2 đường thẳng 2x + y = 12 và y = 8

C(9; 8) là giao của 2 đường thẳng x = 9 và y = 8

D(9; 1) là giao của 2 đường thẳng x = 9 và x + 4y = 13

Tại A(5; 2) thì T = 4.5 + 3.2 = 26 (triệu đồng)

Tại B(2; 8) thì T = 4.2 + 3.8 = 32 (triệu đồng)

Tại C(9; 8) thì T = 4.9 + 3.8 = 60 (triệu đồng)

Tại D(9; 1) thì T = 4.9 + 3.1 = 39 (triệu đồng)

⇒ Chi phí nhỏ nhất là T_min = 26 (triệu đồng)

⇒ Phải thuê 5 chiếc xe loại A và 2 chiếc xe loại B để chi phí bỏ ra là thấp nhất.

* Phương pháp giải:

Gọi số xe loại A cần thuê là: x (chiếc) (x ∈ ℕ);

Số xe loại B cần thuê là: y (chiếc) (y ∈ ℕ)

- tìm điều kiện cho ẩn vừa mới gọi

- lập bất phương trình dựa trên dữ kiện bài toán cho theo ẩn mới gọi

- ta được hệ bất phương trình. Vẽ miền nghiệm của bất phương trình ra và tính toán

* Lý thuyết cần nắm thêm và các dạng bài toán về hệ bất phương trình và miền nghiệm:

Nghiệm của bất phương trình bậc nhất hai ẩn

Xét bất phương trình ax + by + c < 0.

Mỗi cặp số (x₀; y₀) thỏa mãn ax₀ + by₀ + c < 0 được gọi là một nghiệm của bất phương trình đã cho.

Chú ý: Nghiệm của các bất phương trình ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0 được định nghĩa tương tự.

Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x₀; y₀) sao cho ax₀ + by₀ + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.

- Người ta chứng minh được: Mỗi phương trình ax + by + c = 0 (a, b không đồng thời bằng 0) xác định một đường thẳng ∆. Đường thẳng ∆ chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng, trong đó một nửa (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c > 0, nửa còn lại (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c < 0.

Ta có thể biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c < 0 như sau:

Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: ax + by +c = 0.

Bước 2: Lấy một điểm (x₀; y₀) không thuộc ∆. Tính ax₀ +by₀ + c.

+ Nếu ax₀ + by₀ + c < 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (x₀; y₀).

+ Nếu ax₀ + by₀ + c > 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (x₀; y₀).

Chú ý: Đối với các bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 (hoặc ax + by + c ≥ 0) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.

Khái niệm hệ bất phương trình bậc nhất hai ẩn

- Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.

- Trên mặt phẳng tọa độ Oxy, tập hợp các điểm (x₀; y₀) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.

Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ Oxy, ta thực hiện như sau:

- Trên cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.

- Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.

Chú ý: Miền mặt phẳng tọa độ bao gồm một đa giác lồi và phần nằm bên trong đa giác đó được gọi là một miền đa giác.

Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác

Người ta chứng minh được F = ax + by đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của đa giác

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hệ bất phương trình bậc nhất hai ẩn – Toán 10 Kết nối tri thức

Miền nghiệm của hệ bất phương trình: giải SBT kết nối tri thức

Trắc nghiệm Hệ bất phương trình bậc nhất hai ẩn có đáp án – Toán lớp 10

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: