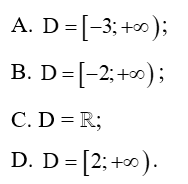1500 câu hỏi ôn tập môn Toán có đáp án (Phần 17)
Bộ 1500 câu hỏi ôn tập môn Toán có đáp án Phần 17 hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
1500 câu hỏi ôn tập Toán (Phần 17)
Câu 1: Tính tổng 3 + 6 + 12 + 24 + … + 3072
Lời giải:
Đặt tổng A = 3 + 6 + 12 + 24 + … + 3072
Ta có: 2A = 6 + 24 + 47 + …. + 6144
⇒ 2A – A = 6144 – 3 = 6141.
Vậy A = 6141.
Câu 2: Chúng tỏ rằng với a, b ∈ ℕ thì ƯCLN (a, b) = ƯCLN (5a + 2b, 7a + 3b)
Lời giải:
Gọi d = ƯCLN (a; b)
Đặt:
a = d.m ; b = d.n ⇒ (m; n) = 1
5a + 2b = d(5m + 2n)
7a + 3b = d(7m + 3n)
Gọi d’ = ƯCLN (5m + 2n; 7m + 3n)
{5m+2n⋮d'7m+3n⋮d'⇒{5m+2n⋮d'2m+n⋮d'⇒{5m+2n⋮d'4m+2n⋮d'⇒m⋮d'
Từ đó suy ra: 2n ⋮ d’ và 3n ⋮ d’ do đó, n⋮ d’
Do đó, d’ thuộc tập ƯC (m;n)
Mà ƯCLN (m; n) = 1 nên d’ = 1
Do đó, ƯCLN (5m + 2n; 7m + 3n) = 1 ⇒ ƯCLN (5a + 2b; 7a + 3b) = d = ƯCLN (a; b)
Câu 3: Giữa các số 7 và 35 hãy đặt thêm 6 số nữa để được một cấp số cộng
Lời giải:
Ta có: u1 = 7 ; u7 = 35
Do dãy số là cấp số cộng nên ta có: u7 = u1 + 6d ⇔ 35 = 7 + 6d ⇔ 6d = 28 ⇔ d = 143
Vậy ta có các số cần tìm là: u2=353;u3=493;u4=21;u5=773;u6=913
Câu 4: Cho 4 điểm A, B, C, D. Chứng minh: →AC+→BD=→AD+→BC .
Lời giải:
Ta có:
VT=→AC+→BD=→AD+→DC+→BC+→CD=→AD+→BC+(→DC+→CD)=→AD+→BC=VP
Câu 5: Cho P = √x√x+2 (x ≥ 0), hãy so sánh P và √P .
Lời giải:
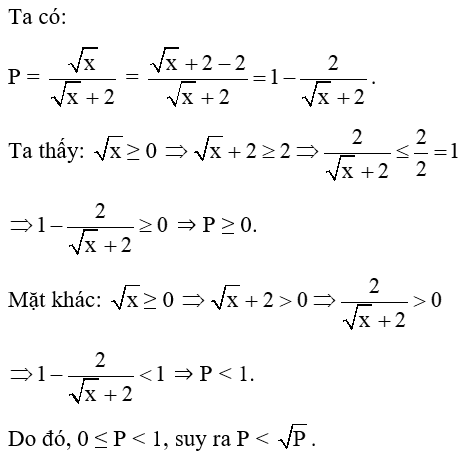
Câu 6: Tìm tập tất cả các nghiệm của phương trình
sin 2x + 2sin2 x – 6sin x – 2cos x + 4 = 0.
Lời giải:
Ta có: sin 2x + 2sin2 x – 6sin x – 2cos x + 4 = 0
⇔ (2sin x cos x – 2cos x) + (2sin2 x – 6sin x + 4) = 0
⇔ 2cos x(sin x – 1) + 2(sin x – 2)(sin x – 1) = 0
⇔ (sin x – 1)(sin x + cos x – 2) = 0
⇔[sin x=1sin x+cos x=2⇔[x=π2+k2π (k∈ℤ)sin(x+π4)=√2 (VN)⇔x=π2+k2π (k∈ℤ).
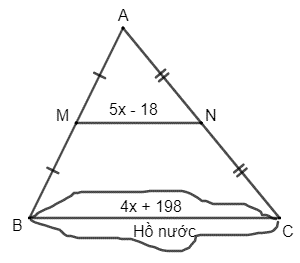
Lời giải:
Xét tam giác ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra MN = 12 BC.
Mà MN = 5x – 18 và BC = 4x + 198 nên ta có: 5x – 18 = 12 (4x + 198)
⇔ 5x – 18 = 2x + 99
⇔ 3x = 117
⇔ x = 39 (mét).
Vậy khoảng cách BC trong hình vẽ đã cho là BC = 4 . 39 + 198 = 354 (mét).
Câu 8: Giải phương trình sau: 5sin x – 2 = 3(1 – sin x)tan2 x.
Lời giải:
Điều kiện: cos x ≠ 0 (*)
Phương trình ⇔ 5sin x – 2 = 3(1 – sin x) . sin2xcos2x
⇔ 5sin x – 2 = 3.(1 – sin x) . sin2x1−sin2x
⇔ 5sin x – 2 = 3sin2x1+sinx
⇒ 2sin2 x + 3sin x – 2 = 0
⇔ [sinx=12 (TM)sinx=−2 (L)
Xét sin x = 12⇔[x=π6+k2πx=5π6+k2π (k∈ℤ) (thỏa mãn điều kiện (*)).
Vậy nghiệm của phương trình là x=π6+k2π và x=5π6+k2π, k∈ℤ.
Câu 9: Chứng minh rằng x8n + x4n + 1 chia hết cho x2n + xn + 1, với mọi số tự nhiên n.
Lời giải:
Ta có: x8n + x4n + 1 = x8n + 2x4n + 1 – x4n = (x4n + 1)2 – (x2n)2
= (x4n + 1 – x2n)(x4n + 1 + x2n)
= (x4n + 1 – x2n)(x4n + 2x2n + 1 – x2n)
= (x4n + 1 – x2n)[(x2n + 1)2 – (xn)2]
= (x4n + 1 – x2n)(x2n – xn + 1)(x2n + xn + 1)
Vậy x8n + x4n + 1 chia hết cho x2n + xn + 1, với mọi số tự nhiên n.
Câu 10: Số các số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 là bao nhiêu?
Lời giải:
Để lập số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 ta thực hiện liên tiếp các công đoạn sau:
- Chọn chữ số hàng đơn vị là chữ số 0, có 1 cách chọn;
- Chọn chữ số hàng chục nghìn, có 9 cách chọn;
- Chọn chữ số hàng nghìn, có 8 cách chọn;
- Chọn chữ số hàng trăm, có 7 cách chọn;
- Chọn chữ số hàng chục, có 6 cách chọn.
Do vậy, theo quy tắc nhân có 1 . 9 . 8. 7 . 6 = 3 024 số tự nhiên có 5 chữ số khác nhau và chia hết cho 10.
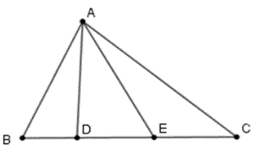
Câu 11: Góc chung là gì?
Lời giải:
Góc chung là khái niệm dùng để chỉ một góc mà nằm ở 2 đa giác khác nhau.
Chẳng hạn tam giác ABC và tam giác ADE có góc chung là góc A.
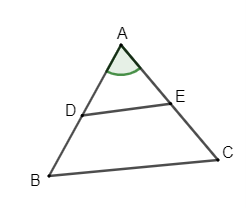
Câu 12: Cho hình vẽ dưới đây:
Góc AEB là góc chung của những tam giác nào:
Lời giải:
Đáp án đúng là: B
Từ hình vẽ ta thấy góc AEB là góc chung của tam giác AEB và tam giác AED.
Câu 13: Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
→AD+→BE+→CF=→AE+→BF+→CD=→AF+→BD+→CE.
Lời giải:
Ta có: →AD+→BE+→CF=(→AE+→ED)+(→BF+→FE)+(→CD+→DF) (quy tắc ba điểm)
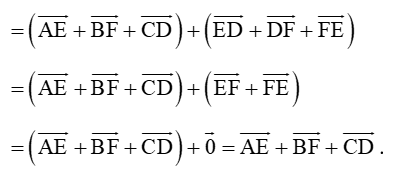
Vậy →AD+→BE+→CF=→AE+→BF+→CD (1).
Lại có: →AE+→BF+→CD=(→AF+→FE)+(→BD+→DF)+(→CE+→ED)

Vậy →AE+→BF+→CD=→AF+→BD+→CE (2).
Từ (1) và (2) suy ra →AD+→BE+→CF=→AE+→BF+→CD=→AF+→BD+→CE (đpcm).
Câu 14: Tìm các ước của 240.
Lời giải:
Ta có: 240 = 24 . 3 . 5.
Số các ước nguyên dương của 240 là: (4 + 1) . (1 + 1) . (1 + 1) = 20.
Các ước nguyên dương của 240 là: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240.
Câu 15: Cho hình bình hành ABCD. Dựng →AM=→BA, →MN=→DA, →NP=→DC, →PQ=→BC .
Lời giải:
Theo quy tắc ba điểm ta có: →AQ=→AM+→MN+→NP+→PQ=→BA+→DA+→DC+→BC
Áp dụng quy tắc hình bình hành ta có: →BA+→BC=→BD, →DA+→DC=→DB (do ABCD là hình bình hành).
Do đó, →AQ=→BD+→DB=→0 (đpcm).
Câu 16: Cho tam giác ABC nhọn. Vẽ AH vuông góc với BC tại H. Chứng minh rằng:
Lời giải:
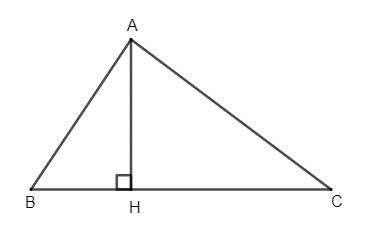
Vì tam giác ABH vuông tại H nên AB2 = AH2 + BH2 (định lí Pythagore).
Suy ra BH2 = AB2 – AH2.
Vì tam giác ACH vuông tại H nên AC2 = AH2 + HC2 (định lí Pythagore).
Do đó ta có: AC2 + BH2 = (AH2 + HC2) + (AB2 – AH2) = AB2 + HC2 (đpcm).
Câu 17: Cho đường thẳng y = 2x + 2.
b) Tính góc tạo bởi đường thẳng y = 2x + 2 với trục hoành Ox.
Lời giải:
a) Với x = 0 thì y = 2, với y = 0 thì x = – 1. Do đó đường thẳng y = 2x + 2 đi qua hai điểm A(0; 2) và B(– 1; 0).
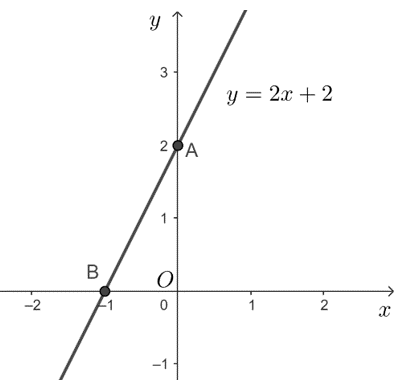
b) Ta có: OA = 2, OB = 1.
Góc tạo bởi đường thẳng y = 2x + 2 với trục hoành Ox là góc ABO.
Xét tam giác ABO vuông tại O, ta có: tanABO = AOBO=21=2 .
Suy ra ^ABO≈63° .
Lời giải:
Ta có: (d1) cắt (d2) tại 1 điểm trên trục tung ⇔ a ≠ a′; b = b′.
Ta có: a ≠ a′ ⇔ 3m ≠ 3 ⇔ m ≠ 1.
b = b′ ⇔ − m2 = m – 2 ⇔ m2 +m - 2 = 0 ⇔ m = 1 (loại) hoặc m = – 2 (t/m).
Vậy m = – 2 thì (d1) cắt (d2) tại 1 điểm trên trục tung.
Câu 19: Chứng minh rằng n3 – n chia hết cho 6 với mọi số nguyên n.
Lời giải:
Ta có: n3 – n = n(n2 – 1) = n(n – 1)(n + 1).
Với n ∈ ℤ thì (n – 1), n, (n + 1) là ba số nguyên liên tiếp.
+) Trong 3 số nguyên liên tiếp sẽ có ít nhất 1 số chẵn nên n(n – 1)(n + 1) chia hết cho 2.
+) Trong 3 số nguyên liên tiếp sẽ có 1 số chia hết cho 3 nên n(n – 1)(n + 1) chia hết cho 3.
Do đó tích n(n – 1)(n + 1) chia hết cho cả 2 và 3.
Mà 2 và 3 là hai số nguyên tố cùng nhau nên tích đó chia hết cho 6 hay n3 – n chia hết cho 6 với mọi số nguyên n.
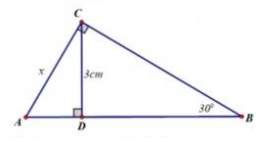
Câu 20: Cho hình vẽ. Biết CD = 3 cm, giá trị của x là:
Lời giải:
Đáp án đúng là: C
Vì tam giác CBD vuông tại D, nên ta có: BC = (cm).
Vì tam giác ACB vuông tại C, nên ta có: x = AC = BC tanB = 6 . tan30° = (cm).
Câu 21: Tìm x, biết: x : 0,25 + x × 11 = 24.
Lời giải:
x : 0,25 + x × 11 = 24
x : + x × 11 = 24
x × 4 + x × 11 = 24
x × (4 + 11) = 24
x × 15 = 24
x = .
Vậy x = .
Câu 22: Mọi số thực đều có căn bậc 3, đúng hay sai?
Lời giải:
+ Căn bậc ba của một số a là số x sao cho x3 = a.
+ Căn bậc ba của số a được kí hiệu là .
Như vậy .
Mọi số thực đều có căn bậc ba.
Câu 23: Tìm m để đa thức A(x) = x3 – 3x2 + 5x + m chia hết cho đa thức B(x) = x – 2.
Lời giải:
Ta có:
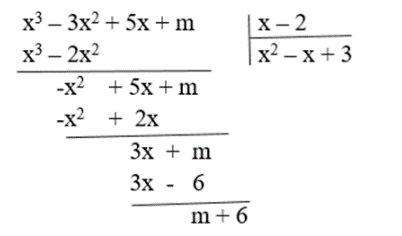
Do đó, A(x) chia hết cho B(x) khi m + 6 = 0, suy ra m = – 6.
Câu 24: Giải phương trình: cos3x – sin3x = 1.
Lời giải:
Ta có: cos3x – sin3x = 1
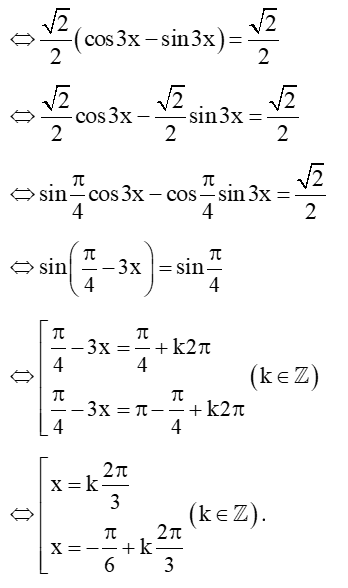
Vậy các nghiệm của phương trình đã cho là , .
Câu 25: Cho ba điểm A(– 4; 0), B(0; 3) và C(2; 1). Xác định tọa độ của vectơ .
Lời giải:
Ta có: .
Do đó, = 2.(4; 3) – (6; 1) = (2 . 4 – 6; 2 . 3 – 1) = (2; 5).
Vậy .
Lời giải:
Gọi x, y (ha) lần lượt là diện tích trồng khoai lang và khoai mì (x, y ≥ 0).
Theo bài ra ta có hệ bất phương trình: .
Số tiền thu được khi trồng x ha khoai lang và y ha khoai mì là F(x; y) = 20x + 25y (triệu đồng).
Bài toán trở thành: Tìm x, y thỏa mãn hệ bất phương trình để F(x; y) = 20x + 25y lớn nhất.
Biểu diễn miền nghiệm của hệ bất phương trình lên mặt phẳng tọa độ.
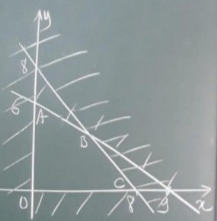
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC với O là gốc tọa độ, A(0; 6), B(6; 2), C(8; 0).
Ta có: F(0; 0) = 0
F(0; 6) = 20 . 0 + 25 . 6 = 150
F(6; 2) = 20 . 6 + 25 . 2 = 170
F(8; 0) = 20. 8 + 25 . 0 = 160
Do đó, F(x; y) lớn nhất tại (x; y) = (6; 2).
Vậy bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì để thu được nhiều tiền nhất.
Câu 27: Nghiệm của phương trình cos x = 0 là
Lời giải:
Đáp án đúng là: C
Ta có: cos x = 0 , k ∈ ℤ.
Lời giải:
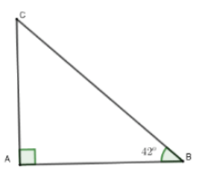
Gọi chiều cao cột đèn là AC, AB là bóng của cột đèn trên mặt đất, AB = 7,5 m.
Góc tạo bởi tia nắng mặt trời với mặt đất là .
Xét tam giác ABC vuông tại A, ta có:
AC = AB . tanB = 7,5 . tan42° ≈ 6,753 (m).
Vậy cột đèn cao khoảng 6,753 m.
Câu 29: Cho biểu thức với x ≥ 0, x ≠ 1, x ≠ 9. So sánh P và P2.
Lời giải:
Ta có:
Với x ≥ 0, x ≠ 1, x ≠ 9 ta có:
hay P > 1 với mọi số thực x nên P < P2.
Lời giải:
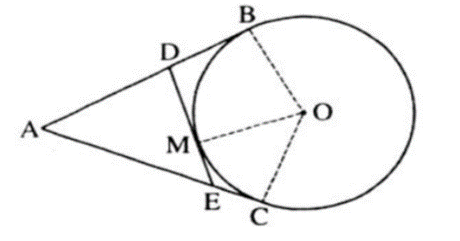
Vì AB, AC là hai tiếp tuyến của (O) lần lượt tại B và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: AB = AC.
Vì DB, DM là hai tiếp tuyến của (O) lần lượt tại B và M. Theo tính chất của hai tiếp tuyến cắt nhau ta có: DB = DM.
Vì EM, EC là hai tiếp tuyến của (O) lần lượt tại M và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: EM = EC.
Chu vi tam giác ADE là:
AD + DE + EA
= AD + (DM + ME) + EA
= (AD + DM) + (ME + EA)
= (AD + DB) + (EC + EA) (do DB = DM, EM = EC)
= AB + AC = 2AB (do AB = AC).
Câu 31: Cho ba điểm A (1; −1), B (2; 1), C (−3; 1). Chứng minh đường thẳng AB vuông góc với đường thẳng AC.
Lời giải:
Gọi pt đường thẳng AB có dạng y = ax + b, do AB đi qua A và B nên:
⇒ y = 2x – 3
Gọi phương trình đường thẳng AC có dạng y = cx +d
Do tích 2 hệ số góc .
Vậy AB và AC vuông góc.
A. 4x – y – 3 = 0; 2x – 3y + 1 = 0;
B. 4x – y – 3 = 0; 2x + 3y + 1 = 0
C. 4x + y – 3 = 0; 2x – 3y + 1 = 0;
D. x – y = 0; 2x – 3y + 1 = 0.
Lời giải:
Gọi (d) là đường thẳng đi qua A và cách đều B, C. Khi đó ta có các trường hợp sau:
TH1: d đi qua trung điểm của BC.
là trung điểm của BC.
là vec tơ chỉ phương của đường thẳng d.
Khi đó (d): – 2(x – 1) + 3(y – 1) = 0 ⟺ 2x – 3y + 1 = 0.
TH2: d song song với BC, khi đó d nhận là vectơ chỉ phương.
Phương trình đường thẳng d là: – 4(x – 1) + y – 1 = 0 ⇔ 4x – y – 3 = 0.
Đáp án đúng là: A
Câu 33: Tìm tập xác định .
Lời giải:
Hàm số xác định khi .
Vậy tập xác định của hàm số là .
Câu 34: Tìm tập xác định D của hàm số .
Lời giải:
Hàm số xác định khi
Vậy tập xác định của hàm số là
Đáp án đúng là B.
Câu 35: Cho tam giác ABC có hb + hc = 2ha. Chứng minh rằng:
Lời giải:
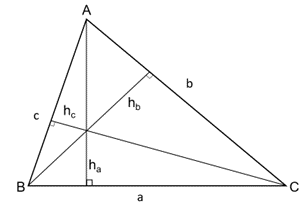
Ta có: hb + hc = 2ha
Áp dụng định lý Sin trong tam giác ABC:
; (R: bán kính đường tròn ngoại tiếp tam giác)
.
Vậy .
Câu 36: Định nghĩa hình chiếu là gì?
Lời giải:
Hình chiếu là hình biểu diễn một mặt nhìn thấy của vật thể đối với người quan sát đứng trước vật thể, phần khuất được thể hiện bằng nét đứt.
Câu 37: Số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là?
Lời giải:
Số tròn chục lớn nhất có 6 chữ số khác nhau là số 987650.
Vậy số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là số 987649.
Lời giải:
Đường thẳng d có dạng y = m(x – 1) = mx – m.
Phương trình hoành độ giao điểm:
với (x ≠ 1)
⇔ x + 2 = (mx – m)(x – 1)
⇔ mx2 – (2m + 1)x + m – 2 = 0 (1)
Để d cắt (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị ⇔ phương trình (1) có hai nghiệm phân biệt x1 < x2 thỏa mãn x1 < 1 < x2 hay (x1 – 1)(x2 – 1) < 0
⇔ m > 0
Vậy m > 0.
Lời giải:
Tọa độ vectơ = (–1 – 5; – 2 – 1) = ( – 6; – 3);
Gọi G (x1; y1) là trọng tâm tam giác ABC.
⇒ Tọa độ trong tâm tam giác ABC là G (2; 1).
Gọi G’ (x2; y2) là trọng tâm tam giác A'B'C'.
Phép tịnh tiến theo véc tơ biến tam giác ABC thành tam giác A'B'C' nên G(2; 1) cũng tịnh tiến theo véc tơ thành G’ (x2; y2).
Ta có: = = ( – 6; – 3)
Vậy G’ (– 4; – 2).
Lời giải:
Tỉ số phần trăm của học sinh nữ so với học sinh nam là :
15 : 25 × 100 = 60 %
Đáp số: 60%.
Câu 41: Một tổ có 25 học sinh nam, 15 học sinh nữ. Hỏi có bao nhiêu cách chọn 1 em làm lớp trưởng?
Lời giải:
Tổng số học sinh của tổ là: 25 + 15 = 40 (học sinh);
Vậy số cách để chọn ngẫu nhiên 1 em làm lớp trưởng là 40 cách.
Lời giải:
Chiều dài của căn phòng :
(m) = 40 (dm)
Ta có: 12 m = 120 dm
Diện tích của căn phòng :
120 × 40 = 4 800 (dm2)
Diện tích mỗi viên gạch men :
8 × 8 = 16 (dm2)
Số viên gạch men dùng để lát căn phòng là
4800 : 16 = 300 (viên gạch men)
Đáp số: 300 viên gạch men
Lời giải:
4 m = 40 dm
Chiều rộng căn phòng là :
40 : ( 4 − 3) × 3 = 120 (dm)
Chiều dài căn phòng là :
40 : ( 4 − 3 ) × 4 = 160 (dm)
Diện tích căn phòng là :
120 × 160 = 19200 (dm2)
Diện tích viên gạch là :
2 × 2 = 4 (dm2)
Cần số gạch để lát căn phòng là :
19200 : 4 = 4800 (viên gạch)
Đáp số: 4800 viên gạch.
Câu 44: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức .
Lời giải:
Điều kiện xác định của biểu thức: 2 ≤ x ≤ 4.
Ta có: (với a, b ≥ 0).
Nên
Do đó GTLN của biểu thức là 2.
Ta có:
Dấu “=” xảy ra khi a = 0 hoặc b = 0;
Áp dụng vào biểu thức:
Đẳng thức xảy ra .
GTNN của biểu thức là: với x = 2 hoặc x = 4.
Câu 45: Tìm x biết: (x – 5)(x – 4) – (x + 1)(x – 2) = 7
Lời giải:
(x – 5)(x – 4) – (x + 1)(x – 2) = 7
⇔ x2 – 4x – 5x + 20 – (x2 – 2x + x – 2) = 7
⇔ x2 – 4x – 5x + 20 – x2 + 2x – x + 2 = 7
⇔ – 8x + 22 = 7
⇔ – 8x = 7 – 22
⇔ – 8x = – 15
Vậy .
Câu 46: Chứng minh A = n3 + (n + 1)3 + (n + 2)3 chia hết cho 9 với mọi n ∈ ℕ*.
Lời giải:
A = n3 + (n + 1)3 + (n + 2)3
= n3 + n3 + 3n2 + 3n + 1 + n3 + 6n2 + 12n + 8
= 3n3 + 9n2 + 15n + 9
= 3n2 (n + 1) + 6n ( n + 1) + 9 (n +1)
= 3 (n + 1)(n2 + 2n + 3)
=3(n + 1)[n (n + 2) + 3]
= 3n (n + 1)(n + 2) + 9( n + 1)
Ta có: n; n + 1; n + 2 là 3 số tự nhiên liên tiếp
⇒ 3n(n + 1)(n + 2) ⋮ 9
Mặc khác: 9(n + 1) ⋮ 9
⇒ A = 3n (n + 1)(n + 2) + 9(n + 1) ⋮ 9.
Vậy A = n3 + (n + 1)3 + (n + 2)3 ⋮ 9.
Lời giải:
Số cân nặng của 25 lít dầu là:
25 × 0,95 = 23,75 (kg)
Tổng số cân nặng của thùng đựng 25 lít dầu là:
23,75 + 8,7 = 32,45 (kg).
Đáp số: 32,45 kg.
a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?
b) Khoảng thời gian từ lúc xuất phát đến khi họ gặp nhau (tính bằng phút)?
Lời giải:
a) Gọi s (km) là khoảng cách từ thị trấn A đến điểm gặp nhau.
Thời gian chuyển động của hai người là như nhau (do xuất phát cùng lúc) nên:
Từ đây ta có s = 11,4 km.
Vậy hai người đi xe đạp sẽ gặp nhau ở vị trí cách thị trấn A là 11,4 km.
b) Thời gian từ lúc xuất phát đến lúc gặp nhau:
(giờ) = 34,2 (phút).
Câu 49: Tìm m để y = 2x3 − mx2 + 2x đồng biến trên (−2; 0).
Lời giải:
Ta có:
(1)
Đề hàm số đồng biến trên (− 2; 0)
với
Xét
Vậy .
Câu 50: Rút gọn phân thức: .
Lời giải:
ĐKXĐ: x ≠ 3; x ≠ − 2.
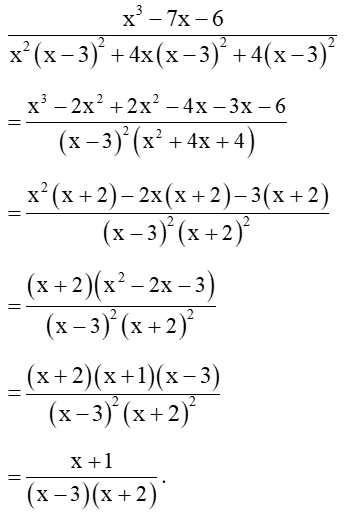
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 15)
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 16)
1500 câu hỏi ôn tập môn Toán có đáp án (Phần 18)
Xem thêm các chương trình khác:
- Các dạng bài tập Tiếng Anh thông dụng nhất
- 3000 câu hỏi ôn tập môn Tiếng Anh có đáp án
- Toàn bộ kiến thức về cụm động từ | Định nghĩa và cách dùng
- 500 đoạn văn Tiếng Anh thông dụng nhất và cách làm
- 1000 câu hỏi ôn tập môn Công nghệ có đáp án
- 1000 câu hỏi ôn tập Giáo dục công dân
- 3000 câu hỏi ôn tập môn Vật lí có đáp án
- Tổng hợp Dạng bài - Công thức môn Vật lí
- Phương trình hóa học | Tổng hợp PTHH của các chất hữu cơ, vô cơ chính xác nhất
- Đồng phân & Công thức cấu tạo của các chất hữu cơ
- Nhận biết các chất Hóa học
- Cấu hình electron
- So sánh bán kính nguyên tử và bán kính ion
- 1000 câu hỏi ôn tập môn Hóa có đáp án
- Wiki các chất hóa học | Định nghĩa, tính chất, nhận biết, điều chế, ứng dụng
- Cách đọc danh pháp hóa học (chương trình mới) đầy đủ nhất
- Công thức Lewis của một số chất thường gặp (chương trình mới)
- Công thức electron của một số chất thường gặp (chương trình mới)
- Công thức cấu tạo của một số chất thường gặp (chương trình mới)
- Công thức hợp chất khí với hidro của các nguyên tố (phổ biến) | Cách viết công thức hợp chất khí với hidro
- Công thức hidroxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức hidroxit cao nhất
- Công thức oxit cao nhất của các nguyên tố (phổ biến) | Cách viết công thức oxit cao nhất
- 2000 câu hỏi ôn tập môn Tin học có đáp án
- 3000 câu hỏi ôn tập môn Lịch sử có đáp án
- 3000 câu hỏi ôn tập môn Địa lí có đáp án
- 2000 câu hỏi ôn tập môn Sinh học có đáp án
- Tổng hợp Dạng bài - Công thức môn Sinh học
- Tổng hợp về các tác giả văn học
- 3000 câu hỏi ôn tập môn Ngữ văn có đáp án
- Tổng hợp kiến thức Ngữ Văn
- Tuyển tập truyện dân gian, truyền thuyết, cổ tích,... Việt Nam
- Tổng hợp các đề đọc - hiểu có đáp án chi tiết
- Trò chơi Powerpoint | Game Powerpoint
- Tổng hợp bài thu hoạch BDTX Giáo viên mầm non (2025) theo Thông tư 12
- Tổng hợp bài thu hoạch BDTX Giáo viên tiểu học (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THCS (2025)
- Tổng hợp bài thu hoạch BDTX Giáo viên THPT (2025)