1500 câu hỏi ôn tập môn Toán có đáp án (Phần 6)

1500 câu hỏi ôn tập Toán (Phần 6)

Câu 1: Tìm m để hàm số $y=x^3-3m{x}^2+3(2m-1)x+1$  đồng biến trên R.

Lời giải: Ta có

$y=x^3-3m{x}^2+3(2m-1)x+1\Rightarrow y^{\text{'}}=3x^2-6mx+3(2m-1);\forall x\in \text{R}.$

Hàm số đồng biến trên R khi và chỉ khi

$y^{\text{'}}\ge 0;\forall x\in \text{R}\iff x^2-2mx+2m-1\ge 0;\forall x\in \text{R}.$

$\iff \left\{\begin{array}{l}a=1>0\\ {\Delta }^{\text{'}}=m^2-2m+1\le 0\end{array}\right.\iff {(m-1)}^2\le 0\iff m=1.$

Vậy m  = 1 là giá trị cần tìm thỏa mãn bài toán.

Câu 2: Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có $BC=\mathrm{3,}\widehat{BAC}={30}^0.$  Tính diện tích tam giác ABC.

Lời giải: Xét bài toán: Tam giác ABC, điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là: $b^2+c^2=5a^2.$

Ta có: Gọi G là giao điểm của hai trung tuyến BM, CN. Áp dụng công thức trung tuyến ta có:

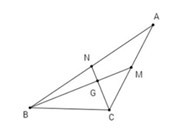
$G{B}^2=\frac{4}{9}B{M}^2=\frac{1}{9}(2a^2+2c^2-b^2);G{C}^2=\frac{4}{9}C{N}^2=\frac{1}{9}(2a^2+2b^2-c^2)$

Áp dụng định lý Pythago cho tam giác vuông BGC, ta có: $B{G}^2+C{G}^2=B{C}^2$

Khi đó ta có:

$\frac{1}{9}(2a^2+2c^2-b^2)+\frac{1}{9}(2a^2+2b^2-c^2)=a^2\iff 4a^2+b^2+c^2=9a^2\iff b^2+c^2=5a^2.$

Quay trở lại bài toán trên, xét tam giác ABC ta có:

$a^2=b^2+c^2-2bc.\cos A=5a^2-2bc.\cos A\Rightarrow bc=\frac{2a^2}{\cos A}.$

Khi đó: $S=\frac{1}{2}bc.\sin A=\frac{1}{2}\frac{2a^2}{\cos A}.\sin A=a^2\tan A=3\sqrt{3}.$

Câu 3: Cho hàm số $y=x^3+m{x}^2+3x-2m+5$  (với m là tham số thực). Với giá trị nào của m thì hàm số đã cho đồng biến trên R.

Lời giải: Ta có: $y=x^3+m{x}^2+3x-2m+5$

$\Rightarrow y^{\text{'}}=3x^2+2mx+3.$

Khi đó xét: ${\Delta }^{\text{'}}=m^2-9.$

Để hàm số trên đồng biến trên R khi và chỉ khi $y^{\text{'}}\ge 0$  với mọi giá trị của m là tham số thực.

Tức là: ${\Delta }^{\text{'}}=m^2-9\ge \iff -3\le m\le 3.$

Vậy $m\in \text{[}-3;3].$

Câu 4: Gọi m là giá trị nhỏ nhất của hàm số $y=x+\frac{4}{x}$  trên khoảng $(0;+\infty ).$  Tìm m.

Lời giải: Hàm số $y=x+\frac{4}{x}$  liên tục trên $(0;+\infty ).$

Ta có: $y^{\text{'}}=1-\frac{4}{x^2}=0\iff \left[\begin{array}{l}x=-2\notin (0;+\infty )\\ x=2\notin (0;+\infty )\end{array}\right.$

Bảng biến thiên của hàm số $y=x+\frac{4}{x}$  trên $(0;+\infty )$  như sau:

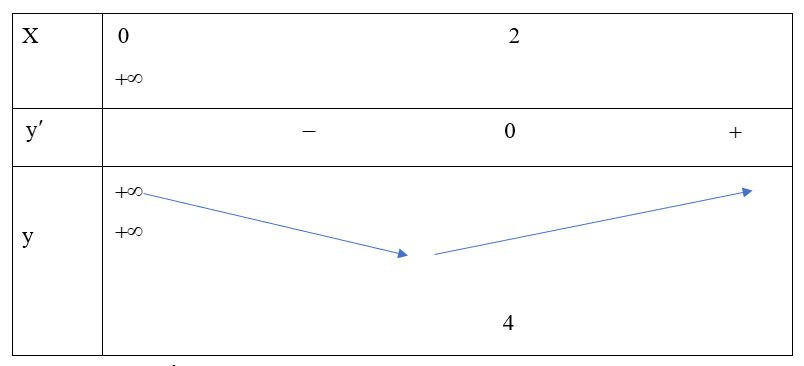
Dựa vào bảng biến thiên, suy ra ta có: $m=\underset{(0;+\infty )}{\min }y=y\left(2\right)=4.$

Nhắc lại: $\underset{x\to 0^{+}}{\lim }y=\underset{x\to 0^{+}}{\lim }\left(x+\frac{4}{x}\right)=+\infty ;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(x+\frac{4}{x}\right)=+\infty .$

Câu 5: Với giá trị nào của m để phương trình $4^x-m{.2}^{x+1}+2m+3=0$ có hai nghiệm $x_1,x_2$ thỏa mãn $x_1+x_2=4.$

Lời giải: Xét phương trình đã cho tương đương với phương trình sau:

$2^{2x}-2m{.2}^x+2m+3=0\left(1\right).$

Đặt $2^x=t(t>0),$  khi đó phương trình (1) trở thành: $t^2-2m.t+2m+3=0\left(2\right).$

Phương trình (1) có hai nghiệm là $x_1,x_2$  khi và chỉ khi phương trình (2) có hai nghiệm $t_1,t_2$dương;

$\iff \left\{\begin{array}{l}{\Delta }^{\text{'}}\ge 0\\ S>0\\ P>0\end{array}\right.\iff \left\{\begin{array}{l}{m}^2-2m-3\ge 0\\ 2m>0\\ 2m+3>0\end{array}\right.\iff m\ge 3.$

Theo định lý Viet ta có: $\left\{\begin{array}{l}{t}_1+t_2=2m\\ t_1.t_2=2m+3\end{array}\right..$  Với $t=2^x$  khi đó ta có:

$t_1.t_2=2^{x_1}{.2}^{x_2}\iff 2m+3=2^{x_1+x_2}\iff 16=2m+3\iff m=\frac{13}{2}.$

Câu 6: Có hai giỏ đựng trứng là giỏ A và giỏ B, các quả trứng trong mỗi giỏ đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng giỏ A nhiều hơn số trứng giỏ B. Lấy ngẫu nhiên một quả trứng, biết xác suất để lấy được hai quả trứng lành là$\frac{55}{84}.$  Tính số trứng lành trong giỏ A.

Lời giải: Gọi a là số trứng lành, b là số trứng hỏng trong giỏ A.

Gọi x là số trứng lành, y là số trứng hỏng trong giỏ B.

Lấy ngẫu nhiên mỗi giỏ 1 quả trứng thì khi đó xác suất để lấy được 2 quả trứng lành là: $\frac{a}{a+b}.\frac{x}{x+y}=\frac{55}{84}.$

Do đó theo giả thiết bài toán ta có:

$\left\{\begin{array}{l}(a.x)⋮55\\ (a+b)(x+y)⋮84\\ a+b+x+y=20\\ (a+b)(x+y)\le {\left(\frac{a+b+x+y}{2}\right)}^2=100\end{array}\right.\Rightarrow \left\{\begin{array}{l}a+b=14\\ x+y=6\\ (a.x)⋮55\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=11\\ x=5\end{array}\right..$

Vậy giỏ A có 11 quả trứng lành.

Câu 7: Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ MN có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P là bao nhiêu vectơ?

Lời giải: Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC.

Suy ra $MN\text{//}AB;MN=\frac{1}{2}AB.\left(1\right)$

Lại có P là trung điểm của AB nên: $AP=BP=\frac{1}{2}AB.\left(2\right)$

Từ (1) và (2) suy ra:  $MN=AP=BP.$

Vậy khi đó số vecto bằng $\overrightarrow{MN}$  mà có điểm đầu và cuối trùng với các điểm trên là: $\overrightarrow{BP};\overrightarrow{PA}.$

Câu 8: Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (ABC') và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu $H_1,H_2$  lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Tính giá trị của  $\frac{V_{\left(H_1\right)}}{V_{\left(H_2\right)}}.$

Lời giải:

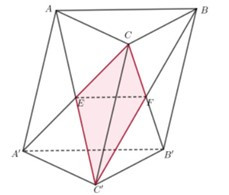
Gọi $E=A{C}^{\text{'}}\cap A^{\text{'}}C$  và $F=B{C}^{\text{'}}\cap B^{\text{'}}C.$  Khi đó (ABC') và (A'B'C') chia khối lăng trụ đều ABC.A'B'C' thành 4 khối đa diện: $CEF{C}^{\text{'}};FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}};FEABC$ và $FEAB{B}^{\text{'}}{A}^{\text{'}}.$

Gọi V là thể tích của khối lăng trụ đều ABC.A'B'C'. Ta có:

$$\begin{gathered} V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{C^{\text{'}\text{'}}.ABC}=\frac{1}{3}V;V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}-V_{CEF{C}^{\text{'}}}; \\ {V}_{FEABC}=V_{C.ABC}-V_{CEF{C}^{\text{'}}}\Rightarrow V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{FEABC}. \end{gathered}$$

Mặt khác: $\frac{V_{CEF{C}^{\text{'}}}}{V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}=\frac{CE}{C{A}^{\text{'}}}\cdot \frac{CF}{C{B}^{\text{'}}}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}\Rightarrow V_{CEF{C}^{\text{'}}}=\frac{1}{4}{V}_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{1}{4}\cdot \frac{1}{3}V=\frac{1}{12}V$

Suy ra 

$$\begin{gathered} V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{FEABC}=V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}-V_{CEF{C}^{\text{'}}}=\frac{1}{3}V-\frac{1}{12}V=\frac{1}{4}V \\ \Rightarrow V_{FEAB{B}^{\text{'}}{A}^{\text{'}}}=V-2.\frac{1}{4}V-\frac{1}{12}V=\frac{5}{12}V. \end{gathered}$$

Do đó $H_1$  là thể tích lớn nhất của khối đa diện $FEAB{B}^{\text{'}}{A}^{\text{'}};H_2$ là thể tích nhỏ nhất của khối đa diện $CEF{C}^{\text{'}}$

Khi đó: $\frac{V_{\left(H_1\right)}}{V_{\left(H_2\right)}}=5.$

Câu 9: Một hình chóp 16 cạnh thì có bao nhiêu mặt?

Lời giải: Hình chóp $S.A_1{A}_2\mathrm{...}{A}_n(n\ge 3)$ có n cạnh bên và n cạnh đáy nên sẽ có 2n cạnh.

Khi đó ta có: $2n=16\iff n=8.$

Vậy hình chóp 16 cạnh sẽ có 8 mặt bên và 1 mặt đáy nên tổng số là 9 mặt.

Câu 10: Với các số a, b > 0 thỏa mãn $a^2+b^2=6ab,$ tính biểu thức ${\log }_2(a+b).$

Lời giải: Ta có: $a^2+b^2=6ab\Rightarrow {(a+b)}^2=8ab\iff a+b=\sqrt{8ab}$

Suy ra ${\log }_2(a+b)={\log }_2\sqrt{8ab}\iff {\log }_2(a+b)=\frac{1}{2}{\log }_2\left(8ab\right)$

Do đó ${\log }_2(a+b)=\frac{1}{2}(3+{\log }_{2}a+{\log }_{2}b).$

Câu 11: Với các số a, b > 0 thỏa mãn $9a^2+b=10ab.$ Hãy chọn đẳng thức đúng sau:

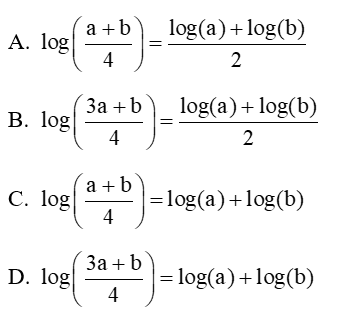
Lời giải: Ta có: $9a^2+b=10ab\iff {\left(\frac{3a+b}{4}\right)}^2=ab.$

Lấy log của cả hai vế của đẳng thức trên thì ta có được:

$\log {\left(\frac{3a+b}{4}\right)}^2=\log \left(ab\right)\Rightarrow 2\log \left(\frac{3a+b}{4}\right)=\log \left(a\right)+\log \left(b\right)\Rightarrow \log \left(\frac{3a+b}{4}\right)=\frac{\log \left(a\right)+\log \left(b\right)}{2}.$

Chọn đáp án B.

Câu 12: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?

Lời giải: Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:

+ Chia khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành hai khối lăng trụ tam giác bằng nhau: ABC.A'B'C' và  BCD.B'C'D'

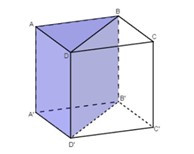
+ Tiếp theo, lần lượt chia khối lăng trụ $ABD.A^{\text{'}}{B}^{\text{'}}{D}^{\text{'}}$ và $BCD.B^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành ba tứ diện: $DAB{B}^{\text{'}};DA{A}^{\text{'}}B$ và  $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}.$

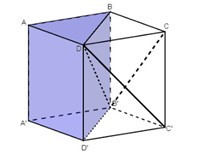
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:

-        Hai khối tứ diện DABB' và DAA'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB')         (1)

-        Hai khối tứ diện DAA'B' và DD'A'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B'A'D)         (2)

Từ (1) và (2) suy ra ba khối tứ diện $DAB{B}^{\text{'}},DA{A}^{\text{'}}{B}^{\text{'}}$ và $D{D}^{\text{'}}{A}^{\text{'}}{B}^{\text{'}}$ bằng nhau.

-        Tương tự, ba khối tứ diện $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}$ cũng bằng nhau.

Vậy khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ được chia thành sáu khối tứ diện bằng nhau.

Câu 13: Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.

Lời giải: Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic, …

Khối đa diện không lồi trong thực tế: cái bàn, cái ghế, …

Câu 14: Đếm số đỉnh, số cạnh của khối đa diện lồi đều như hình vẽ sau:

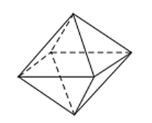
Lời giải: Khối bát diện đều trên có 6 đỉnh và 12 cạnh.

Câu 15: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi φ là góc giữa SD và mặt phẳng (ABCD). Tính cot φ?

Lời giải:

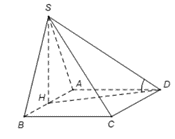
Gọi H là trung điểm của AB. Khi đó ta có $SH\perp AB\Rightarrow SH\perp \left(ABCD\right)$  nên hình chiếu của SD trên (ABCD) là HD.

Do đó $\widehat{SD,\left(ABCD\right)}=\widehat{SD,HD}=\widehat{SDH}.$

Mặt khác tam giác SAB đều cạnh a nên $SH=\frac{a\sqrt{3}}{2}.$

Suy ra $HD=\sqrt{A{H}^2+A{B}^2}=\frac{a\sqrt{5}}{2}.$

Khi đó xét tam giác vuông SHD, ta có: $\cot \widehat{SHD}=\frac{DH}{SH}=\frac{5}{\sqrt{15}}.$

Câu 16:By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.

Lời giải:

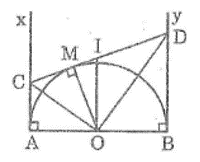
Theo tính chất hai tiếp tuyến cắt nhau ta có:

CA = CM

DB = DM

Suy ra: AC + BD = CM + DM = CD

Chu vi hình thang ABDC bằng: AB + BD + DC + CA = AB + 2CD

Vì đường kính AB của (O) không thay đổi nên chu vi hình thang nhỏ nhất khi CD nhỏ nhất

Ta có: CD   AB nên CD nhỏ nhât khi và chỉ khi CD = AB

Khi đó $\text{CD // AB}\iff \text{OM }\perp \text{AB}$

Vậy khi M là giao điểm của đường thẳng vuông góc với AB tại O với nửa đường tròn (O) thì hình thang ABDC có chu vi nhỏ nhất.

Câu 17:Cho nửa đường tròn (O) có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn cùng thuộc một nửa mặt phẳng có bờ là AB ). Qua một điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By theo thứ tự ở C và D. Gọi $N=AD\cap BC,H=MN\cap AB.$Chọn câu đúng nhất.

A. $MN\perp AB$

B. MN > NH

C. Cả A, B đều đúng      

D. Cả A, B đều sai.

Lời giải:

Theo tính chất hai tiếp tuyến cắt nhau ta có: AC = CM và BD = DM

AC // BD (vì cùng vuông góc vớiAB )

Theo hệ quả của định lý Ta – lét ta có:

$\frac{\text{CN}}{\text{BN}}\text{ = }\frac{\text{AC}}{\text{BD}}\Rightarrow \frac{\text{CN}}{\text{BN}}\text{ = }\frac{\text{CM}}{\text{DM}}$

Theo định lý Ta – Lét đảo ta đượcMN // BD.

Mà $\text{BD\hspace{0.33em}}\perp \text{AB}\Rightarrow \text{MN}\perp \text{AB}$

Theo hệ quả của định lý Ta – Lét ta có:

$\frac{\text{NH}}{\text{BD}}\text{=}\frac{\text{AH}}{\text{AB}}\text{ = }\frac{\text{CN}}{\text{CB}}\text{ = }\frac{\text{MN}}{\text{BD}}\Rightarrow \text{MN = NH}$

nên B sai.

Đáp án cần chọn là: A

Câu 18:Rút gọn phân thức: $\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\left(\text{x - y}\right)}^{\text{2}}\text{ + }{\left(\text{y - z}\right)}^{\text{2}}\text{ + }{\left(\text{z - x}\right)}^{\text{2}}}$

Lời giải:

$\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\left(\text{x - y}\right)}^{\text{2}}\text{ + }{\left(\text{y - z}\right)}^{\text{2}}\text{ + }{\left(\text{z - x}\right)}^{\text{2}}}$

$\begin{array}{l}\text{= }\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\text{x}}^{\text{2}}{\text{ - 2xy + y}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ - 2yz + z}}^{\text{2}}{\text{ + z}}^{\text{2}}{\text{ - 2xz + x}}^{\text{2}}}\\ \text{= }\frac{\left(\text{x + y + z}\right)\text{ . }\left({\text{x}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ +z}}^{\text{2}}\text{ - xy - yz - zx}\right)}{\text{2 . }\left({\text{x}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ + z}}^{\text{2}}\text{ - xy - yz - zx}\right)}\\ \text{= }\frac{\text{x + y + z}}{\text{2}}\end{array}$

Câu 19:Tìm các chữ số a, b, c, d sao cho tổng abc + dba chia hết cho aa và được thương là aa (abc, dba là các số có 3 chữ số theo thứ tự là a, b, c và d, b, a; aa là số có 2 chữ số đều bằng a).

Lời giải:

Ta có $\left(\overline{abc}+\overline{dba}\right):\overline{\text{aa}}=\overline{\text{aa}}$  nên $\left(\overline{abc}+\overline{dba}\right)=\overline{\text{aa}}.\overline{\text{aa}}=121a.a$

Vì $\overline{abc}+\overline{dba}<2000$  nên a.a.121 < 2000

Suy ra a.a < 17 nên a ∈ {1; 2; 3; 4}.

TH1. a = 1, ta có: $\overline{abc}+\overline{dba}=\mathrm{1.1.121}=121<2000$

Mà $\overline{abc}+\overline{dba}$  không thể nhỏ hơn 200 nên loại.

TH2. a = 2, ta có: $\overline{abc}+\overline{dba}=\mathrm{2.2.121}=484<2000$

Ở hàng đơn vị ta có c + 2 = 4 thì c = 2

Ở hàng chục ta có: b + b = 8 ⇔ b = 4 ⇒ d = 2 hoặc b + b = 18 ⇔ b = 9 ⇒ d = 1.

Vậy a = 2, b = 4, c = 2, d = 2 hoặc a = 2, b = 9, c = 2, d = 2.

TH3. a = 3, ta có: $\overline{abc}+\overline{dba}=\mathrm{3.3.121}=1089<2000$

Ở hàng đơn vị ta có c + 3 = 9 thì c = 6

Ở hàng chục ta có: b + b = 8 ⇔ b = 4 ⇒ d = 7 hoặc b + b = 18 ⇔ b = 9 ⇒ d = 6.

Vậy a = 3, b = 4, c = 6, d = 7 hoặc a = 3, b = 9, c = 6, d = 6.

TH4. a = 4, ta có: $\overline{abc}+\overline{dba}=\mathrm{4.4.121}=1936<2000$

Vì $\overline{abc}=\overline{4bc}<500$  và $\overline{dba}<1000$ . Do đó trường hợp này loại.

Câu 20:Giải phương trình : x⁴ - 8x² + x + 12 = 0

Lời giải:

Đặt t bằng x²

Đk $t\ge 0$

Ta có phương trình

t² - 8t + t +12 = 0

$\text{Δ = }{\left(\text{-8}\right)}^{\text{2}}\text{ - 1 . }\left(\text{t + 12}\right)$

= 64 – t - 12

= 52  -  t

Suy ra 52  -  t  > 0⇔ - t > - 52⇔ t < 52

${\text{t}}_{\text{1}}\text{ = - }\frac{\text{- 8 - }\sqrt{\text{52}}}{\text{2 . 1}}\text{ = 4 + }\sqrt{\text{3}}$ (nhận)

${\text{t}}_{\text{2}}\text{ = - }\frac{\text{- 8 + }\sqrt{\text{52}}}{\text{2 . 1}}\text{ = 4 - }\sqrt{\text{3}}$ (nhận )

Câu 21:Điểm thuộc đồ thị hàm số y = -2x là:

A. M(-2; -2)

B. N(1; 4)

C. P(-1; -2)

D. Q(-1; 2)

Lời giải:

Thay các điểm M, N, P vào hàm số đều không thỏa mãn, chỉ có điểm Q(-1; 2) thỏa mãn vì 2 = -2 . (-1)

Chọn đáp án D

Câu 22:Cho hình chữ nhật ABCD có chiều dài 6 cm, chiều rộng 4 cm (như hình vẽ). Diện tích hình tam giác MDC bên trong hình chữ nhật là bao nhiêu?

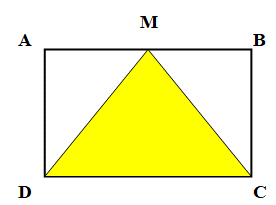
Lời giải:

Diện tích hình tam giác MDC là:

6 × 4 : 2 = 12(cm²)

Câu 23: Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Chứng minh

$\frac{1+\sqrt{1+x^2}}{x}+\frac{1+\sqrt{1+y^2}}{y}+\frac{1+\sqrt{1+z^2}}{z}\le xyz$

Lời giải:

Áp dụng bất đăng thức Cauchy, ta có $\left\{\begin{array}{l}2xy\le x^2+y^2\\ 2yz\le y^2+z^2\\ 2zx\le z^2+x^2\end{array}\right.$

⇒ 2(xy + yz + zx) ≤ 2(x² + y² + z²)

⇔ xy + yz + zx ≤ x² + y² + z²

⇔ 3(xy + yz + zx) ≤ x² + y² + z² + 2(xy + yz + zx)

⇔ 3(xy + yz + zx) ≤ (x + y + z)²

$\iff xy+yz+zx\le \frac{{\left(x+y+z\right)}^2}{3}$.

Áp dụng bất đẳng thức Cauchy, ta có $\frac{4+\left(1+x^2\right)}{2}\ge \sqrt{4\left(1+x^2\right)}$

Ta có

$\frac{1+\sqrt{1+x^2}}{x}=\frac{2+\sqrt{4\left(1+x^2\right)}}{2x}\le \frac{2+\frac{4+\left(1+x^2\right)}{2}}{2x}=\frac{4+4+\left(1+x^2\right)}{4x}=\frac{9+x^2}{4x}$ .

Chứng minh tương tự, ta có $\frac{1+\sqrt{1+y^2}}{y}\le \frac{9+y^2}{4y}$  và $\frac{1+\sqrt{1+z^2}}{z}\le \frac{9+z^2}{4z}$ .

Khi đó

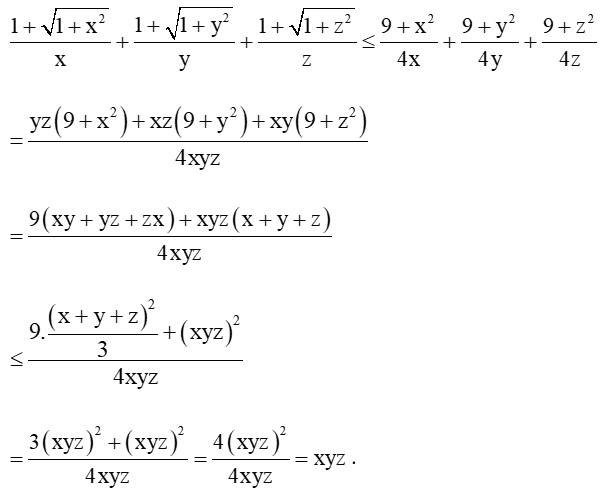
Dấu “=” xảy ra $\iff x=y=z=\sqrt{3}$ .

Vậy ta có điều phải chứng minh.

Câu 24: Cho 3 số thực dương x, y, z thỏa mãn x + y + z + 2 = xyz. Chứng minh rằng

$x+y+z+6\ge 2\left(\sqrt{yz}+\sqrt{zx}+\sqrt{xy}\right)$

Lời giải:

Theo đề, ta có x + y + z + 2 = xyz

⇔ (xy + yz + zx) + 2(x + y + z) + 3 = xyz + xy + yz + zx + x + y + z + 1

⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (xy + x + y + 1)(z + 1)

⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (x + 1)(y + 1)(z + 1)

$\iff \frac{1}{z+1}+\frac{1}{x+1}+\frac{1}{y+1}=1$.

Đặt $a=\frac{1}{x+1};b=\frac{1}{y+1};c=\frac{1}{z+1}$

Khi đó ta có a + b + c = 1 và

$x=\frac{1-a}{a}=\frac{b+c}{a};y=\frac{1-b}{b}=\frac{a+c}{b};z=\frac{1-c}{c}=\frac{a+b}{c}$ .

Ta có

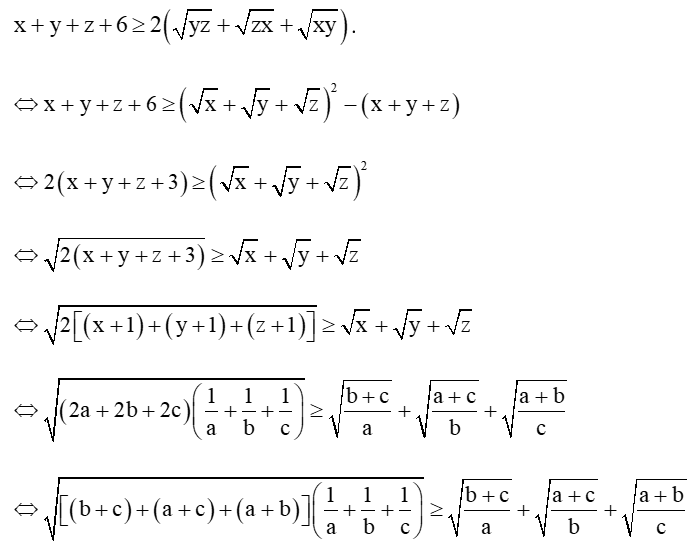
Dấu “=” xảy ra $\iff a=b=c=\frac{1}{3}\iff x=y=z=2$ .

Vậy ta có điều phải chứng minh.

Câu 25: Giải phương trình: $1+\sin x+\cos x=2\cos \left(\frac{x}{2}-\frac{\pi }{4}\right)$

Lời giải:

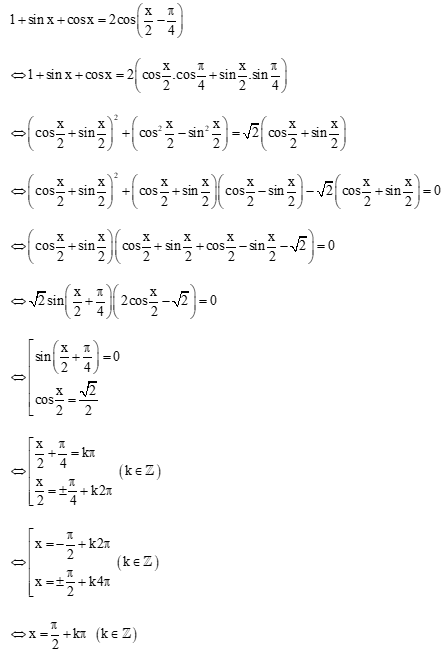
Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ .

Câu 26: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở giữa là 3 m x 6 m. Hãy tính khoảng cách giữa hai điểm A và B.

A. 13 m;

B. 14 m;

C. 12 m;

D. 10 m.

Lời giải:

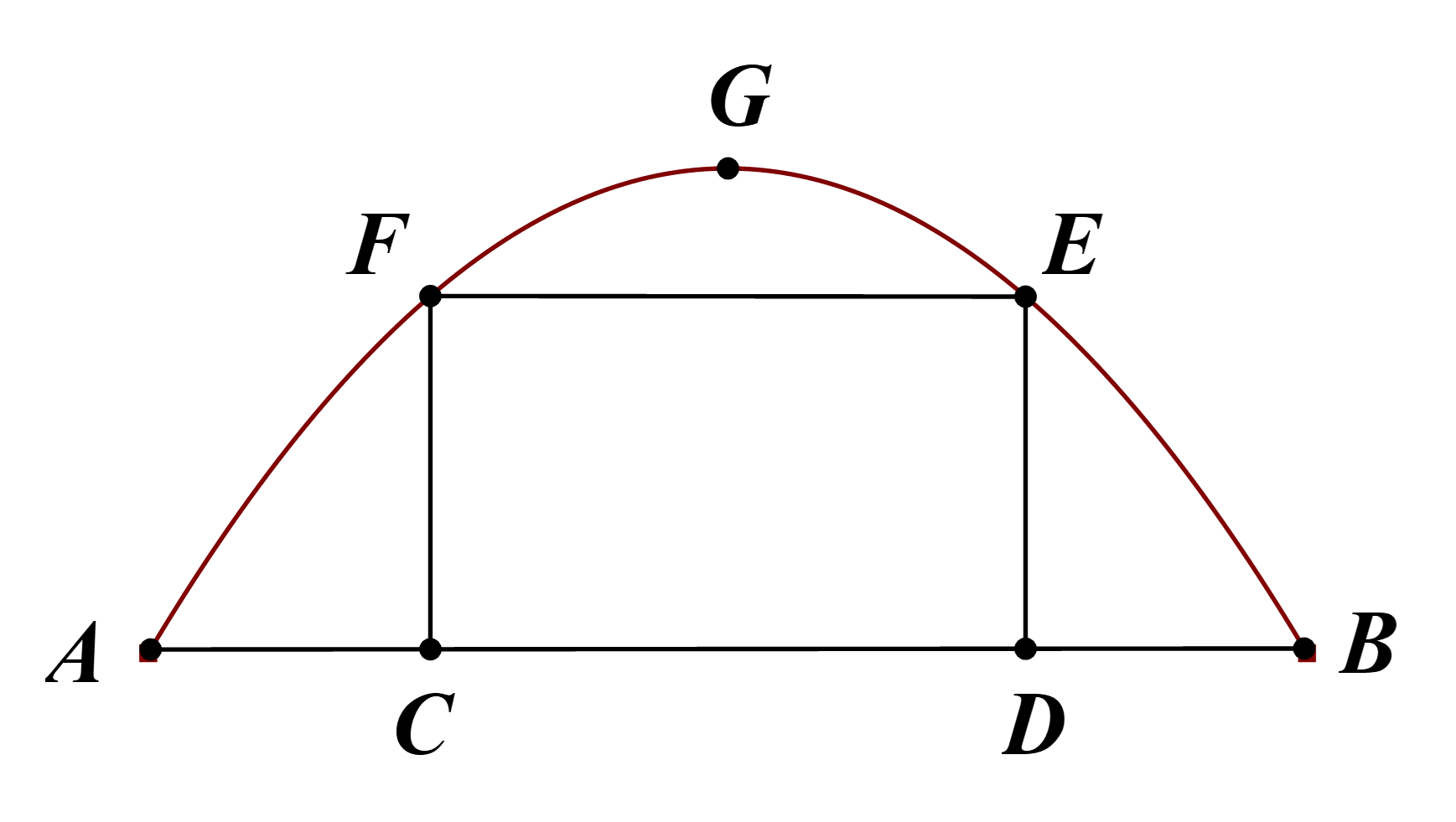
Chọn hệ trục tọa độ Oxy như hình vẽ.

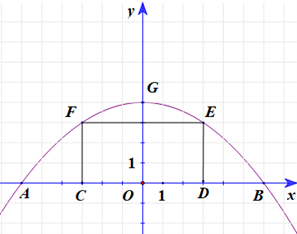
Phương trình parabol có dạng (P): y = ax² + bx + c (a < 0).

Ta có G(0; 4) ∈ (P) ⇒ c = 4.

Theo đề, ta có kích thước cửa ở giữa là 3 m x 6 m.

Suy ra E(3; 3), F(–3; 3).

Ta có $\left\{\begin{array}{l}E\in \left(P\right)\\ F\in \left(P\right)\end{array}\right.$

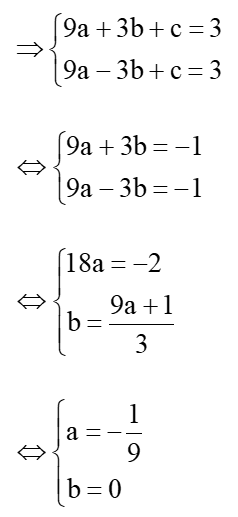
So với điều kiện a < 0, ta nhận $a=-\frac{1}{9}$ .

Khi đó phương trình parabol (P): $y=-\frac{1}{9}{x}^2+4$ .

Phương trình hoành độ giao điểm của (P) và trục Ox là: $-\frac{1}{9}{x}^2+4=0$

⇔ x² = 36

⇔ x = ±6.

Suy ra tọa độ A(–6; 0), B(6; 0).

Do đó AB = 12 m.

Vậy ta chọn phương án C.

Câu 27: $\frac{2}{3}$  ngày bằng bao nhiêu giờ?

Lời giải:

1 ngày có 24 giờ.

Suy ra $\frac{2}{3}$  ngày bằng: $\frac{2}{3}\times 24=16$  (giờ).

Vậy $\frac{2}{3}$  ngày bằng 16 giờ.

Câu 28: Đổi: 4 giờ 30 phút = … giờ.

Lời giải:

30 phút = $\frac{30}{60}$  giờ = $\frac{1}{2}$  giờ.

4 giờ 30 phút = $4+\frac{1}{2}$  giờ = $\frac{9}{2}$  giờ.

Vậy 4 giờ 30 phút = $\frac{9}{2}$  giờ.

Câu 29: Tính nhanh:

a) 4524 – (864 – 999) – (36 + 3999);

b) 1000 – (137 + 572) + (263 – 291);

c) –329 + (15 – 101) – (25 – 440).

Lời giải:

a) 4524 – (864 – 999) – (36 + 3999)

= 4524 – 864 + 999 – 36 – 3999

= 4524 – (864 + 36) + (999 – 3999)

= 4524 – 900 – 3000

= 624.

b) 1000 – (137 + 572) + (263 – 291)

= 1000 – 137 – 572 + 263 – 291

= 1000 + 263 – (137 + 572 + 291)

= 263 + 1000 – 1000

= 263.

c) –329 + (15 – 101) – (25 – 440)

= –329 + 15 – 101 – 25 + 440

= 440 – (329 + 101) – (25 – 15)

= 440 – 430 – 10

= 0.

Câu 30: Công thức tính bài toán sản lượng lớp 5.

Lời giải:

Bước 1: Tìm chiều dài, chiều rộng của thửa ruộng hoặc mảnh đất.

Bước 2: Tính diện tích của thửa ruộng hoặc mảnh đất đó.

Bước 3: Tính sản lượng bằng cách lấy diện tích nhân với năng suất (trên một đơn vị diện tích).

Câu 31: Một thửa ruộng hình chữ nhật có chiều dài 80 m và chiều dài bằng $\frac{5}{4}$  chiều rộng. Người ta mở rộng thửa ruộng đó theo chiều dài thêm 25 m, thửa ruộng thành một hình chữ nhật mới và cấy lúa trên đó. Ước tính cứ 100 m² đạt năng suất 50 kg. Tính sản lượng thóc thu được ở thửa ruộng đó.

Lời giải:

Chiều rộng của thửa ruộng là: $80:\frac{5}{4}=64$  (m)

Diện tích của thửa ruộng sau khi mở rộng chiều dài thêm 25 m là:

(80 + 25) ⨯ 64 = 6720 (m²)

Sản lượng thóc thu được ở thửa ruộng đó là: 6720 : 100 ⨯ 50 = 3360 (kg)

Vậy sản lượng thóc thu được ở thửa ruộng đó là 3360 kg.

Câu 32: Tính $M=\sqrt{1-\frac{\sqrt{3}}{2+\sqrt{3}}}$ .

Lời giải:

$$\begin{gathered} M=\sqrt{1-\frac{\sqrt{3}}{2+\sqrt{3}}} \\ =\sqrt{1-\frac{2\sqrt{3}-3}{1}}=\sqrt{1-2\sqrt{3}+3} \\ =\sqrt{{\left(1-\sqrt{3}\right)}^2}=\sqrt{3}-1 \end{gathered}$$

Câu 33: Tính $A=\frac{1+\frac{\sqrt{3}}{2}}{1+\sqrt{1+\frac{\sqrt{3}}{2}}}+\frac{1-\frac{\sqrt{3}}{2}}{1-\sqrt{1-\frac{\sqrt{3}}{2}}}$ .

Lời giải:

$$\begin{gathered} A=\frac{1+\frac{\sqrt{3}}{2}}{1+\sqrt{1+\frac{\sqrt{3}}{2}}}+\frac{1-\frac{\sqrt{3}}{2}}{1-\sqrt{1-\frac{\sqrt{3}}{2}}} \\ =\frac{\frac{2+\sqrt{3}}{2}}{1+\sqrt{\frac{4+2\sqrt{3}}{4}}}+\frac{\frac{2-\sqrt{3}}{2}}{1-\sqrt{\frac{4-2\sqrt{3}}{4}}} \\ =\frac{\frac{2+\sqrt{3}}{2}}{1+\sqrt{\frac{{\left(\sqrt{3}+1\right)}^2}{4}}}+\frac{\frac{2-\sqrt{3}}{2}}{1-\sqrt{\frac{{\left(\sqrt{3}-1\right)}^2}{4}}} \\ =\frac{\frac{2+\sqrt{3}}{2}}{1+\frac{\sqrt{3}+1}{2}}+\frac{\frac{2-\sqrt{3}}{2}}{1-\frac{\sqrt{3}-1}{2}} \\ =\frac{\frac{2+\sqrt{3}}{2}}{\frac{3+\sqrt{3}}{2}}+\frac{\frac{2-\sqrt{3}}{2}}{\frac{3-\sqrt{3}}{2}} \\ =\frac{2+\sqrt{3}}{3+\sqrt{3}}+\frac{2-\sqrt{3}}{3-\sqrt{3}} \\ =\frac{\left(2+\sqrt{3}\right)\left(3-\sqrt{3}\right)+\left(2-\sqrt{3}\right)\left(3+\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)} \\ =\frac{\left(6+\sqrt{3}-3\right)+\left(6-\sqrt{3}-3\right)}{9-3} \end{gathered}$$

$=\frac{6}{6}=1$

Vậy A = 1.

Câu 34: Trên cùng một hệ trục tọa độ, cho ba đường thẳng (d₁), (d₂) và (d₃) lần lượt là đồ thị của các hàm số y = –2x + 2,$y=\frac{1}{2}x-3$ , y = mx + n.

a) Vẽ hai đồ thị (d₁) và (d₂) trên cùng một hệ trục tọa độ.

b) Tìm m, n để đường thẳng (d₃) song song với (d₁) và cắt (d₂) tại điểm có tung độ bằng –1.

Lời giải:

a) Bảng giá trị của (d₁):

x	0	1	2
y	2	0	–2

Bảng giá trị của (d₂):

x	0	2	4
y	–3	–2	–1

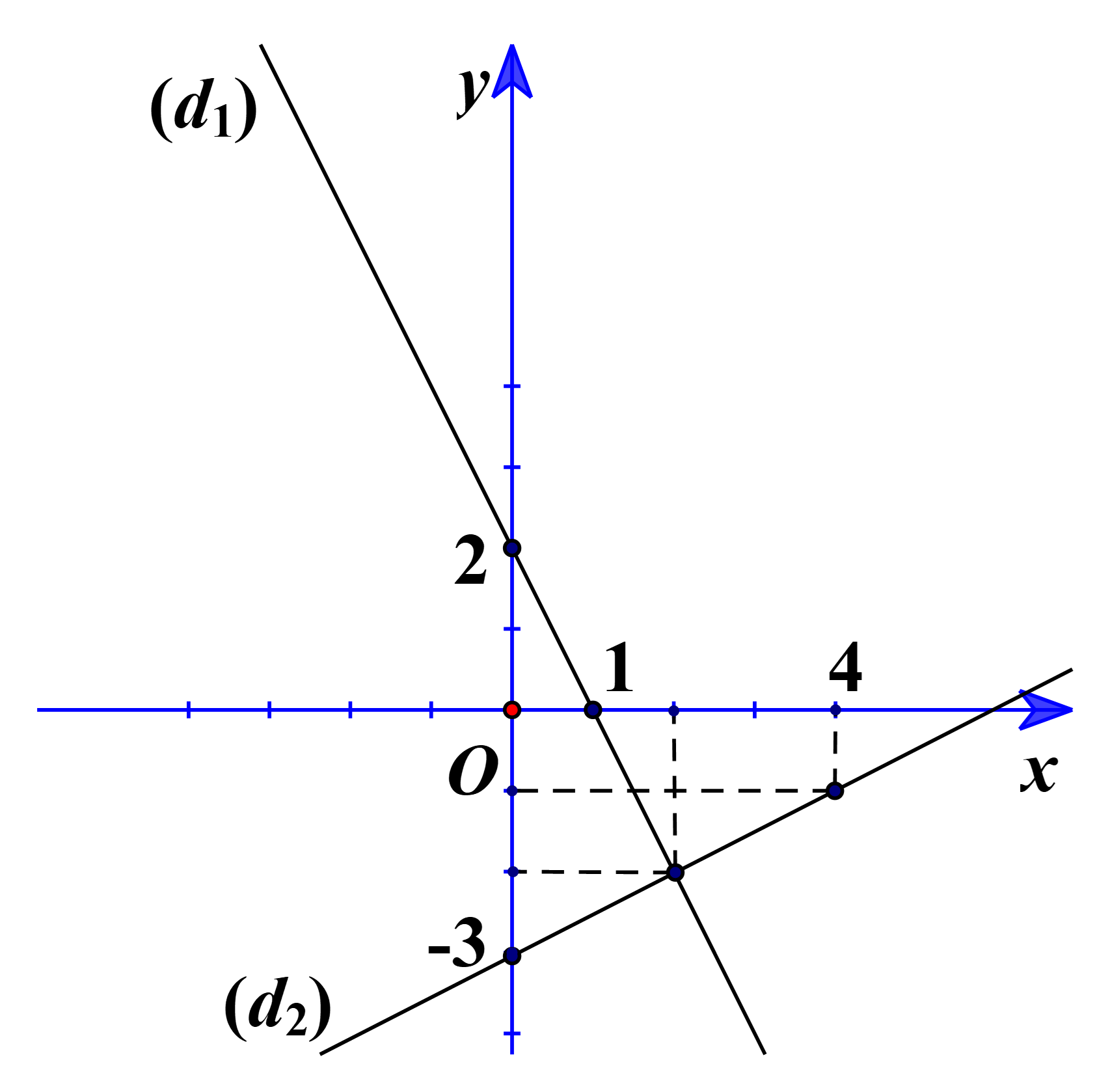
b) Vì (d₃) // (d₁) nên phương trình (d₃) có dạng: y = –2x + n (n ≠ 2).

Tức là, m = –2.

Gọi A(x_A; y_A) là giao điểm của (d₃) và (d₂).

Suy ra tọa độ A(x_A; –1).

Ta có A(x_A; –1) ∈ (d₂).

Suy ra $-1=\frac{1}{2}{x}_A-3$ .

Khi đó x_A = 4.

Vì vậy tọa độ A(4; –1).

Ta có A(4; –1) ∈ (d₃).

Suy ra –1 = –2.4 + n.

Do đó n = 7 (nhận).

Vì vậy m = –2, n = 7.

Câu 35: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d₁): y = –x + 2 và (d₂): $y=\frac{1}{4}x$ .

1) Vẽ (d₁) và (d₂) trên cùng hệ trục tọa độ Oxy.

2) Lấy điểm B trên (d₂) có hoành độ bằng –4. Viết phương trình đường thẳng (d₃) song song với (d₁) và qua điểm B.

3) Tìm tọa độ giao điểm của (d₁) và (d₂) bằng phép tính.

Lời giải:

1) Bảng giá trị của (d₁):

x	0	1	2
y	2	1	0

Bảng giá trị của (d₂):

x	–4	0	4
y	–1	0	1

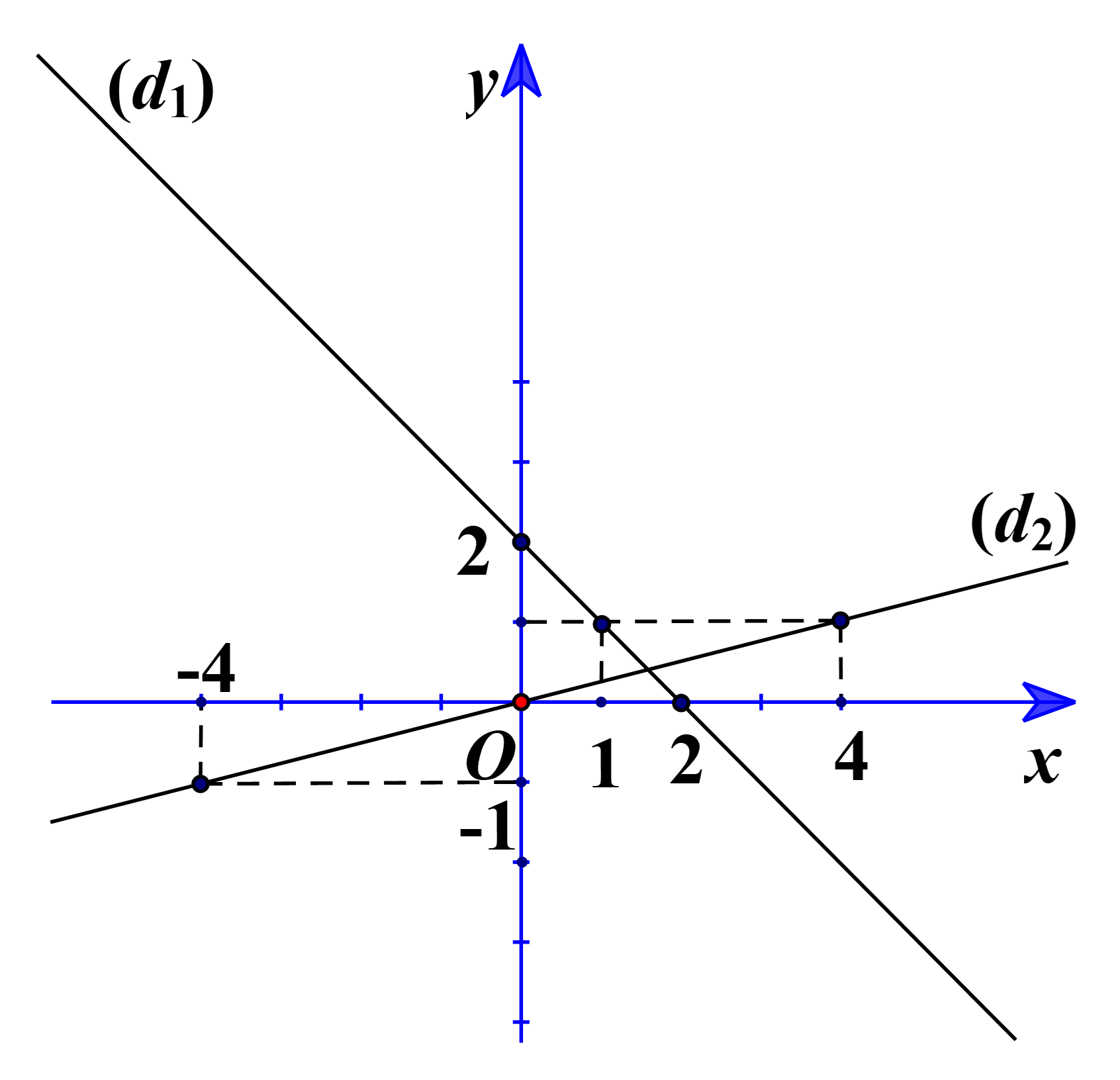
2) Gọi B(–4; y_B).

Ta có B(–4; y_B) ∈ (d₂).

Suy ra $y=\frac{1}{4}.\left(-4\right)=-1$ .

Do đó tọa độ B(–4; –1).

Vì (d₃) // (d₁) nên phương trình (d₃) có dạng: y = –x + m (m ≠ 2).

Ta có B(–4; –1) ∈ (d₃).

Suy ra –1 = 4 + m.

Do đó m = –5 (nhận)

Vậy phương trình (d₃): y = –x – 5.

3) Phương trình hoành độ giao điểm của (d₁) và (d₂): $-x+2=\frac{1}{4}x$ .

$\iff \frac{5}{4}x=2$

$\iff x=\frac{8}{5}$.

Với $x=\frac{8}{5}$ , ta có: $y=-\frac{8}{5}+2=\frac{2}{5}$ .

Vậy giao điểm của (d₁) và (d₂) là điểm $E\left(\frac{8}{5};\frac{2}{5}\right)$ .

Câu 36: Giải bất phương trình: $\frac{x-3}{2-x}\le 0$ .

Lời giải:

Đặt $f\left(x\right)=\frac{x-3}{2-x}$ .

Bảng xét dấu:

x	2                    3
f(x)	–           ||        +         0         –

Dựa vào bảng xét dấu, ta có $f\left(x\right)\le 0\iff \left[\begin{array}{l}x<2\\ x\ge 3\end{array}\right.$

Vậy tập nghiệm của bất phương trình đã cho là $S=\left(-\infty ;2\right)\cup \left[3;+\infty \right)$ .

Câu 37: Giải phương trình: 2x² – 8x = –1.

Lời giải:

2x² – 8x = –1

⇔ 2(x² – 4x + 4) = 7

⇔ 2(x – 2)² = 7

$$\begin{gathered} \iff {\left(x-2\right)}^2=\frac{7}{2} \\ \iff \left[\begin{array}{l}x-2=\sqrt{\frac{7}{2}}=\frac{\sqrt{14}}{2}\\ x-2=-\sqrt{\frac{7}{2}}=-\frac{\sqrt{14}}{2}\end{array}\right. \\ \iff \left[\begin{array}{l}x=2+\frac{\sqrt{14}}{2}=\frac{4+\sqrt{14}}{2}\\ x=2-\frac{\sqrt{14}}{2}=\frac{4-\sqrt{14}}{2}\end{array}\right. \end{gathered}$$

Vậy tập nghiệm của phương trình đã cho là $S=\left\{\frac{4+\sqrt{14}}{2};\frac{4-\sqrt{14}}{2}\right\}$ .

Câu 38: Trong mặt phẳng tọa độ Oxy, cho 5 điểm có tọa độ là các số nguyên. Chứng minh rằng có ít nhất một trung điểm của đoạn thẳng tạo thành từ 5 điểm đã cho có tọa độ là các số nguyên (Trong mặt phẳng tọa độ Oxy: Tọa độ trung điểm bằng trung bình cộng các tọa độ tương ứng của hai đầu đoạn thẳng).

Lời giải:

Xét 1 điểm có tọa độ (x; y) bất kì trong mặt phẳng tọa độ Oxy (x; y là các số nguyên).

Do 1 giá trị x hoặc y chỉ nhận 1 trong 2 giá trị chẵn, lẻ.

Suy ra có tất cả 2.2 = 4 bộ số mà (x; y) có thể nhận.

Mà theo đề bài, ta có tất cả 5 điểm có tọa độ là các số nguyên.

Do đó theo nguyên lí Dirichle, tồn tại ít nhất 2 điểm có cùng tọa độ chẵn, lẻ.

Vậy có ít nhất một trung điểm của đoạn thẳng tạo thành từ 5 điểm đã cho có tọa độ là các số nguyên (điều phải chứng minh).

Câu 39: Tìm m để đường thẳng y = mx + 3m + 2 và đường thẳng y = 2x – 1 cắt nhau tại 1 điểm có tung độ bằng 2.

Lời giải:

Gọi d₁: y = mx + 3m + 2, d₂: y = 2x – 1.

Để hai đường thẳng trên cắt nhau thì m ≠ 2.

Gọi A(x_A; y_A) là giao điểm của d₁ và d₂.

Suy ra tọa độ A(x_A; 2).

Ta có A(x_A; 2) ∈ d₂.

Suy ra 2 = 2.x_A – 1.

Do đó $x_A=\frac{3}{2}$.

Vì vậy tọa độ $A\left(\frac{3}{2};2\right)$ .

Ta có $A\left(\frac{3}{2};2\right)\in d_1$ .

Suy ra $2=\frac{3}{2}m+3m+2$ .

Do đó $\frac{9}{2}m=0$ .

Vì vậy m = 0 (thỏa mãn).

Vậy m = 0 thỏa mãn yêu cầu bài toán.

Câu 40: Cho hình bình hành ABCD, qua C kẻ đường thẳng song song BD cắt AB ở E, cắt AD ở F.

a) Tứ giác BECD là hình gì? Vì sao?

b) Chứng minh 3 đường thẳng AC, BF, DE đồng quy (cùng đi qua 1 điểm).

Lời giải:

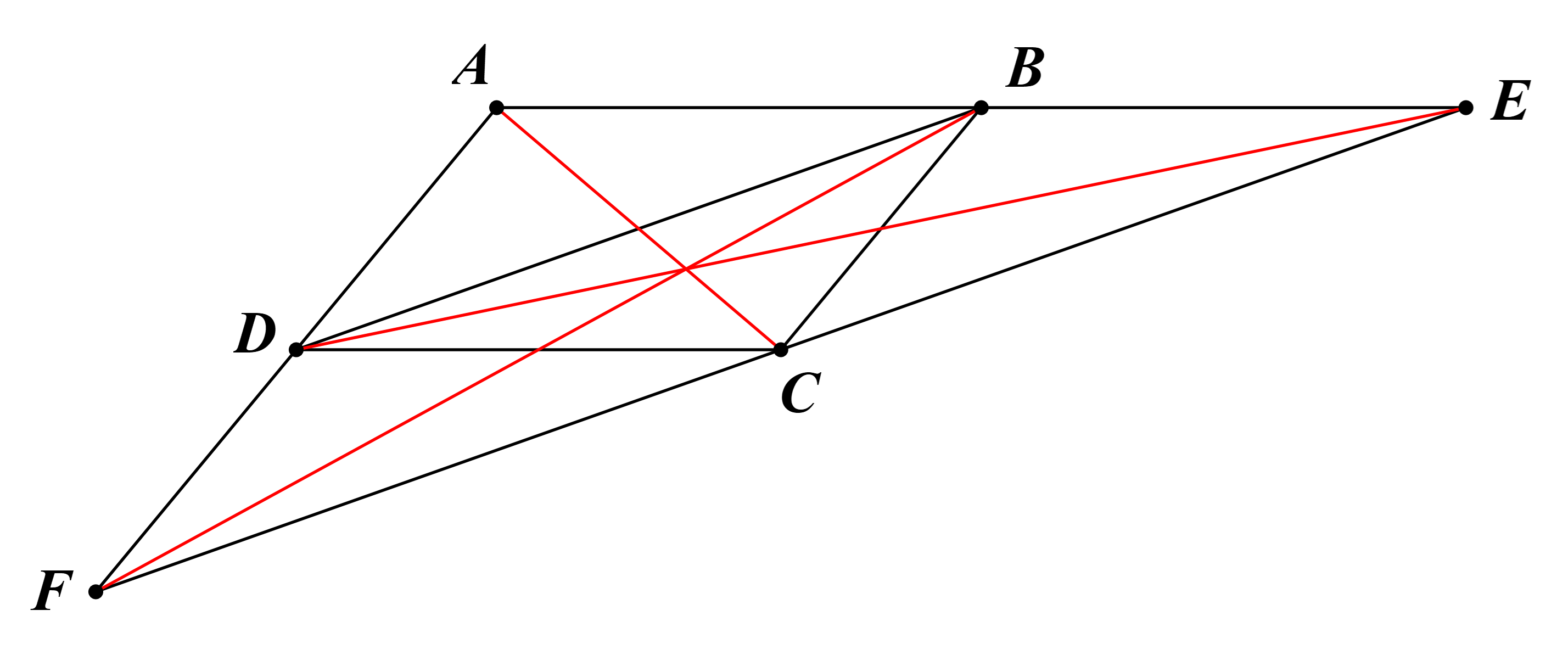
a) Tứ giác BECD là hình bình hành vì BE // CD (giả thiết) và CE // BD (giả thiết).

b) Ta có DF // BC (giả thiết) và BD // CF (giả thiết).

Suy ra BCFD là hình bình hành.

Do đó CF = BD   (1)

Lại có BECD là hình bình hành (chứng minh trên).

Suy ra CE = BD   (2)

Từ (1), (2), suy ra CF = CE.

Do đó CA là đường trung tuyến của tam giác AEF  (*)

Ta có FD = BC (do BCFD là hình bình hành) và AD = BC (do ABCD là hình bình hành).

Suy ra DF = AD.

Do đó DE là đường trung tuyến của tam giác AEF   (**)

Chứng minh tương tự, ta được BF là đường trung tuyến của tam giác AEF   (***)

Từ (*), (**), (***), suy ra ba đường thẳng AC, BF, DE đồng quy tại trọng tâm của tam giác AEF.

Vậy ta có điều phải chứng minh.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 7)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 8)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 9)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 10)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 11)