1500 câu hỏi ôn tập Toán (Phần 1)

Câu 1: Cho tam giác ABC, M, N, P được xác định bởi véctơ$\overrightarrow{MA}=-\frac{3}{4}\overrightarrow{BM},\overrightarrow{AN}=-3\overrightarrow{CN},\overrightarrow{CP}=\frac{1}{4}\overrightarrow{PB}$.

Chứng minh M, N, P thẳng hàng?

Lời giải:

Ta có: $\overrightarrow{MA}=-\frac{3}{4}\overrightarrow{BM}=\frac{3}{4}\overrightarrow{MB};\overrightarrow{AN}=-3\overrightarrow{CN}=3\overrightarrow{NC};\overrightarrow{CP}=\frac{1}{4}\overrightarrow{PB}$

Ta lại có: $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\frac{3}{4}\overrightarrow{MB}+3\overrightarrow{NC}=\frac{3}{4}\overrightarrow{MP}+\frac{3}{4}\overrightarrow{PB}+3\overrightarrow{NP}+3\overrightarrow{PC}$

$\iff \overrightarrow{MN}=\frac{3}{4}\overrightarrow{MP}+3\overrightarrow{CP}+3\overrightarrow{NP}-3\overrightarrow{CP}=\frac{3}{4}\overrightarrow{MP}+3\overrightarrow{NP}$

$\iff \overrightarrow{MP}+\overrightarrow{PN}=\frac{3}{4}\overrightarrow{MP}+3\overrightarrow{NP}$

$\iff \frac{1}{4}\overrightarrow{MP}=4\overrightarrow{NP}\iff \overrightarrow{MP}=16\overrightarrow{NP}$

Do đó M, N, P thằng hàng.

Câu 2: Cho a,b ≠ -2 thỏa mãn (2a + 1) (2b + 1) = 9

Tính giá trị biểu thức $M=\frac{1}{2+a}+\frac{1}{2+b}$.

Lời giải:

Ta có: $2b+1=\frac{9}{2a+1}\Rightarrow b=\frac{4-a}{2a+1}\Rightarrow b+2=\frac{4-a}{2a+1}+2=\frac{3a+6}{2a+1}$

$M=\frac{1}{a+2}+\frac{2a+1}{3a+6}=\frac{1}{a+2}+\frac{2a+1}{3\left(a+2\right)}=\frac{3+2a+1}{3\left(a+2\right)}=\frac{2\left(a+2\right)}{3\left(a+2\right)}=\frac{2}{3}$.

Câu 3: Chứng minh các bất đẳng thức: $\frac{1}{a}+ \frac{1}{b}\ge \frac{4}{a+b}$ với a > 0, b > 0

Lời giải:

Xét hiệu

$\frac{1}{a}+ \frac{1}{b}-\frac{4}{a+b}=\frac{b\left(a+b\right)+a\left(a+b\right)-4ab}{ab\left(a+b\right)}=\frac{a^2-2ab+b^2}{ab\left(a+b\right)}=\frac{{\left(a-b\right)}^2}{ab\left(a+b\right)}\ge 0$, vì a, b > 0

Xảy ra đẳng thức khi và chỉ khi a = b.

Câu 4: Cho a lớn hơn 0 và b lớn hơn 0. Chứng minh rằng

$\left(\frac{1}{a}+\frac{1}{b}\right)\left(a+b\right)\ge 4$

Lời giải:

$$\begin{gathered} \left(\frac{1}{a}+\frac{1}{b}\right)\left(a+b\right)\ge 4 \\ \iff 1+\frac{b}{a}+\frac{a}{b}+1\ge 4 \\ \iff \frac{b^2+a^2}{ab}\ge 2 \end{gathered}$$

Vì a > 0 và b > 0  ⇒ ab > 0

Vậy $\frac{b^2+a^2}{ab}\ge 2\iff b^2+a^2\ge 2ab$

$\iff {\left(a-b\right)}^2\ge 0$.

Vậy bất đẳng thức được chứng minh.

Câu 5: Trên bàn cờ 5 x 4 ô vuông như hình vẽ, người chơi chỉ được di chuyển quân theo các cạnh của hình vuông, mỗi bước đi được 1 cạnh. Có bao nhiêu cách di chuyển quân từ điểm A tới điểm B bằng 9 bước ?

Lời giải:

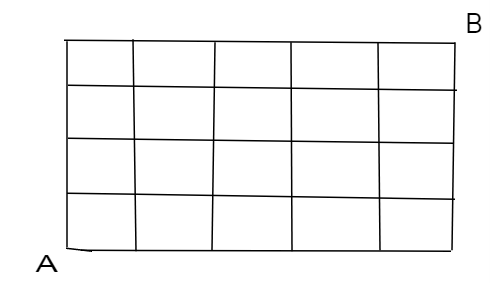
Để đi từ A đến B qua 9 bước thì chỉ có 1 cách đi duy nhất là các bước đi đều phải đi từ dưới lên hoặc đi từ trái qua phải.

Gọi M(i; j) là điểm bất kì nằm ở hàng i cột j với $i=\overline{1;5}$ và $j=\overline{1;6}$.

Để đến được điểm M thì chỉ có 3 cách đi đó là từ điểm có tọa độ (i − 1; j) hoặc (i; j − 1) như hình vẽ dưới:

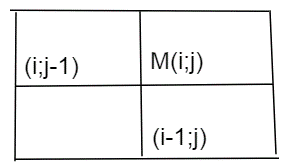
Gọi số cách đi đến M là f(i; j) thì theo quy tắc cộng ta có

$f\left(i;j\right)=f\left(i-1;j\right)+f\left(i;j-1\right)$

Từ đó ta được kết quả sau:

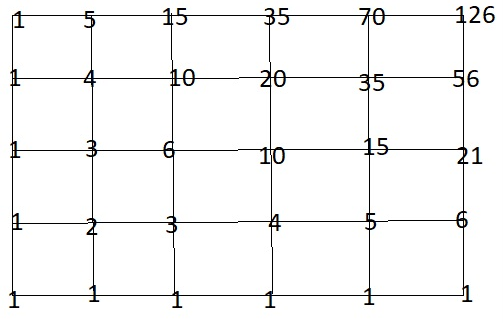
Vậy có 126 cách đi thỏa mãn

Câu 6: Căn bậc hai của (a – b)² là:

A. a – b;

B. b – a;

C. |a – b|;

D. a – b và b – a.

Lời giải:

Ta có: $\sqrt{{\left(a-b\right)}^2}=\left|a-b\right|$.

Đáp án đúng là: C.

Câu 7: Rút gọn

a) $\sqrt{{\left(\sqrt{2}-1\right)}^2}$;

b) $\sqrt{{\left(2-\sqrt{5}\right)}^2}$.

Lời giải:

a) $\sqrt{{\left(\sqrt{2}-1\right)}^2}=\left|\sqrt{2}-1\right|=\sqrt{2}-1$ (vì $\sqrt{2}-1$)

Vậy $\sqrt{{\left(\sqrt{2}-1\right)}^2}=\sqrt{2}-1$.

b) $\sqrt{{\left(2-\sqrt{5}\right)}^2}=\left|2-\sqrt{5}\right|=\sqrt{5}-2$ (vì $\sqrt{5}>2$)

Vậy $\sqrt{{\left(2-\sqrt{5}\right)}^2}=\sqrt{5}-2$.

Câu 8: Tìm x

$3^{2x}-3^x=72$

Lời giải:

$3^{2x}-3^x=72$

Ta có: $3^1=3;3^2=9;3^3=27;3^4=81$ mà 81 – 9 = 72 nên x = 2

$\Rightarrow 3^{2.2}-3^2=72$

Câu 9: $2^x+2^x+1=72\left(x\in N\right)$. Tìm x

Lời giải:

$\begin{array}{l}{2}^x+2^{x+1}=72\text{}\\ \Rightarrow 2^x+2.2^x=72\text{}\\ \Rightarrow 3.2^x=72\text{}\\ \Rightarrow 2^x=72:3\text{}\\ \Rightarrow 2^x=24\text{}\\ \Rightarrow 2^x=2^{4,58}\text{}\\ \Rightarrow x=4,58\text{}\end{array}$

Mà $x\in N\Rightarrow$Không có x

Vậy không tìm được x

Câu 10: Cho $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$. Tính giá trị biểu thức $P=\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ac}{b^2}$.

Lời giải:

$$\begin{gathered} P=\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ac}{b^2} \\ \Rightarrow P=\frac{abc}{c^3}+\frac{abc}{a^3}+\frac{abc}{b^3} \\ \Rightarrow P=abc\left(\frac{1}{c^3}+\frac{1}{a^3}+\frac{1}{b^3}\right) \end{gathered}$$

Vì $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$

$$\begin{gathered} \Rightarrow \frac{1}{a}+\frac{1}{b}=-\frac{1}{c} \\ \Rightarrow {\left(\frac{\text{1}}{\text{a}}\text{+}\frac{\text{1}}{\text{b}}\right)}^{\text{3}}\text{=}{\left(-\frac{\text{1}}{\text{c}}\right)}^{\text{3}} \\ \Rightarrow \frac{\text{1}}{{\text{a}}^{\text{3}}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{3}}}\text{+}\frac{\text{3}}{\text{ab}}\left(\frac{\text{1}}{\text{a}}\text{+}\frac{\text{1}}{\text{b}}\right)\text{=}-\frac{\text{1}}{{\text{c}}^{\text{3}}} \\ \Rightarrow \frac{\text{1}}{{\text{a}}^{\text{3}}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{3}}}\text{+}\frac{\text{1}}{{\text{c}}^{\text{3}}}\text{+}\frac{\text{3}}{\text{ab}}\left(-\frac{\text{1}}{\text{c}}\right)\text{=0} \\ \Rightarrow \frac{\text{1}}{{\text{a}}^{\text{3}}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{3}}}\text{+}\frac{\text{1}}{{\text{c}}^{\text{3}}}\text{=}\frac{\text{3}}{\text{abc}}\left(\text{1}\right) \end{gathered}$$

Thay (1) vào P ta được

$\text{P = abc.}\frac{\text{3}}{\text{abc}}$

⇒ P = 3.

Câu 11: Cho a, b, c khác nhau đôi một và $\frac{\text{1}}{\text{a}}\text{+}\frac{\text{1}}{\text{b}}\text{+}\frac{\text{1}}{\text{c}}\text{=\hspace{0.17em}0}$. Rút gọn biểu thức:

a) $\text{M=}\frac{\text{1}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{1}}{{\text{c}}^{\text{2}}\text{+2ab}}\text{;}$

b) $\text{N=}\frac{\text{bc}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{ca}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{ab}}{{\text{c}}^{\text{2}}\text{+2ab}}\text{;}$

c) $\text{P=}\frac{{\text{a}}^{\text{2}}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{{\text{b}}^{\text{2}}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{{\text{c}}^{\text{2}}}{{\text{c}}^{\text{2}}\text{+2ab}}$.

Lời giải:

Từ giả thiết suy ra ab + bc + ac = 0 nên

$a^2+2bc=a^2+bc+\left(-ab-ac\right)=a\left(a-b\right)-c\left(a-b\right)=\left(a-b\right)\left(a-c\right)$

Tương tự: $b^2+2ac=\left(b-a\right)\left(b-c\right)$,

$c^2+2ab=\left(c-a\right)\left(c-b\right)$

a) $\text{M=}\frac{\text{1}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{1}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{1}}{{\text{c}}^{\text{2}}\text{+2ab}}=\frac{b-c+c-a+a-b}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=0$

b) $$\begin{gathered} \text{N=}\frac{\text{bc}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{\text{ca}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{\text{ab}}{{\text{c}}^{\text{2}}\text{+2ab}} \\ =\frac{bc}{\left(a-b\right)\left(a-c\right)}+\frac{ca}{\left(b-a\right)\left(b-c\right)}+\frac{ab}{\left(c-a\right)\left(c-b\right)} \\ =1 \end{gathered}$$

c) $$\begin{gathered} \text{P=}\frac{{\text{a}}^{\text{2}}}{{\text{a}}^{\text{2}}\text{+2bc}}\text{+}\frac{{\text{b}}^{\text{2}}}{{\text{b}}^{\text{2}}\text{+2ac}}\text{+}\frac{{\text{c}}^{\text{2}}}{{\text{c}}^{\text{2}}\text{+2ab}} \\ =\frac{a^2}{\left(a-b\right)\left(a-c\right)}+\frac{b^2}{\left(b-a\right)\left(b-c\right)}+\frac{c^2}{\left(c-a\right)\left(c-b\right)}=1 \end{gathered}$$.

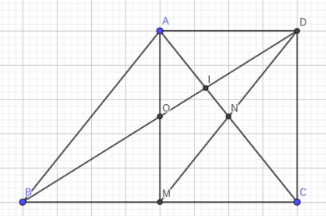
Câu 12: Cho $\Delta ABC$ cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.

a) CMR : tứ giác ADCM là hình chữ nhật

b) CMR : tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM

c) BD cắt AC tại I. CMR : $DI=\frac{2}{3}OB$

Lời giải:

a.Ta có: N là trung điểm AC
M,D đối xứng qua N→ N là trung điểm MD

$\Rightarrow AC\cap DM=N$ là trung điểm mỗi đường
Vì $\text{AM}\perp \text{BC}$

$\Rightarrow AM\perp MC\Rightarrow AMCD$ là hình chữ nhật
 b.Vì $\text{ΔABC}$ cân tại $A,AM\perp BC\Rightarrow M$ là trung điểm $BC\Rightarrow MB=MC$

 AMCD là hình chữ nhật ⇒ AD // CM, AD = CM
⇒ AD // BM, AD = BM

⇒ ABMD là hình bình hành

$\Rightarrow AM\cap BD$ tại trung điểm mỗi đường
Gọi $AM\cap BD=O$

⇒ O là trung điểm AM, BD
⇒ BD đi qua trung điểm O của AM
c) Vì O, N là trung điểm AM,DM và $AN\cap DO=I$

⇒ I là trọng tâm $\text{ΔMAD}$

$\Rightarrow DI=\frac{2}{3}DO$

Vì O là trung điểm BD → OB = OD

$\Rightarrow DI=\frac{2}{3}OB$

Câu 13: Hai số có hiệu là 95. Nếu xóa bỏ chữ số 5 ở tận cùng của số lớn thì ta được số bé. Tìm tổng hai số đó?

Lời giải:

Nếu xóa bỏ chữ số 5 ở tận cùng của số lớn thì được số bé
Suy ra số lớn gấp 10 lần số bé và hơn 5 đơn vị
Số bé là: (95 - 5) :(10 - 1) x 1 = 10
Suy ra số lớn là: 105
Tổng 2 số đó là: 105 + 10 = 115.

Câu 14: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?

Lời giải:

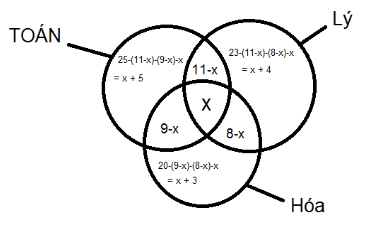
Gọi số học sinh giỏi cả ba môn của lớp 10 A là x ( x > 0, x ∈ N )

Mà số học sinh lớp 10A là 45 học sinh .

⇒ x + 5 + x + 4 + x + 3 + 11 - x + 9 - x + 8 - x + x = 45

⇒ 40 + x = 45

⇒ x = 5 (TM)

Vậy có 5 bạn giỏi cả ba môn toán lý và hóa.

Câu 15: Lớp 10A có 45 học sinh trong đó có 15 bạn được xếp lực học giỏi, 20 bạn được xếp hạnh kiểm tốt, có 10 bạn vừa được xếp lực học giỏi vừa được hạnh kiểm tốt. Số học sinh của lớp 10A được nhận khen thưởng nếu đạt được học lực giỏi hoặc hạnh kiểm tốt là:

A. 10.

B. 35.

C. 30.

D. 25.

Lời giải:

Đáp án: D

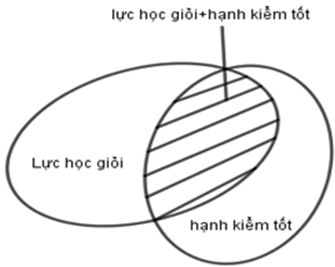
Số học sinh chỉ đạt học lực giỏi là: 15 – 10 = 5 (học sinh).

Số học sinh chỉ đạt hạnh kiểm tốt là: 20 – 10 = 10 (học sinh).

Số học sinh được nhận thưởng là: 5 + 10 + 10 = 25 (học sinh).

Câu 16: Hình nón được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng hính chiếu cạnh, thì hình chiếu đứng và hình chiếu cạnh có hình dạng gì?

Lời giải:

Hình nón được tạo thành khi quay hình tam giác vuông một vòng quanh một cạnh góc vuông cố định.

Nếu đặt mặt đáy của hình nón song song với mặt phẳng hình chiếu cạnh, thì hình chiếu đứng là hình tam giác cân và hình chiếu cạnh có hình tròn.

Câu 17: Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu cạnh thì hình chiếu đứng và hình chiếu cạnh có hình dạng:

A. Hình tròn, hình tam giác cân

B. Hình tam giác cân, hình tròn

C. Hình tròn, hình tam giác đều

D. Hình tam giác đều, hình tròn

Lời giải:

Đáp án đúng: A

Nếu đặt mặt đáy của hình nón song song với mặt phẳng hình chiếu cạnh, thì hình chiếu đứng là hình tam giác cân và hình chiếu cạnh có hình tròn.

Câu 18: Cho tam giác ABC đều. Gọi M, N lần lượt là các điểm trên cạnh AB, BC sao cho BM = BN. Gọi G là trọng tâm tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác GIC.

Lời giải:

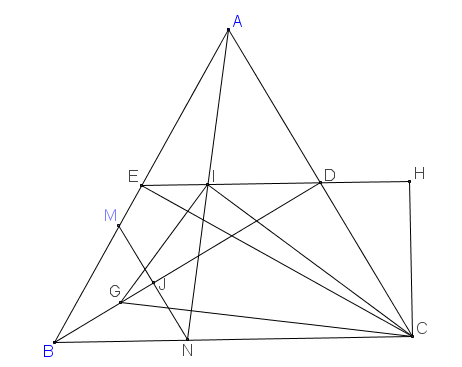
Gọi E, D lần lượt là trung điểm AB, AC, ta có I, E, D thẳng hàng
MN cắt BD tại J, hạ CH vuông góc ED tại H

Có $DH=\frac{DC}{2}=\frac{ED}{2}\Rightarrow \frac{ED}{EH}=\frac{2}{3}$

Có $\frac{BG}{BD}=\frac{BG}{BJ}.\frac{BJ}{BD}=\frac{2}{3}.\frac{BN}{BC}=\frac{ED}{EH}.\frac{EI}{ED}$

$\Rightarrow \frac{BG}{BD}=\frac{EI}{EH}\iff \frac{BG}{EI}=\frac{BD}{EH}\left(1\right)$

Ta có △CBD ∼ △CEH (g, g)
$\Rightarrow \frac{CB}{CE}=\frac{BD}{EH}=\frac{BG}{EI}$
⇒ △CBG ∼△CEI (c, g, c) (2)

$\left(2\right)\Rightarrow \widehat{BCG}=\widehat{ECI}$

$\iff \widehat{BCG}+\widehat{GCE}=\widehat{GCE}+\widehat{ECI}$

$\iff \widehat{BCE}=\widehat{GCI}$

$\left(2\right)\Rightarrow \frac{BC}{EC}=\frac{GC}{IC}\left(4\right)$

từ (3, 4) → △BEC∼△GIC (c, g, c)

$\iff \widehat{I}=90°;\widehat{G}=60°$ (đpcm).

Câu 19: Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông góc AI cắt AB, AC tại M, N. Chứng minh rằng:

a) $\frac{BM}{CN}=\frac{B{I}^2}{C{I}^2}$

b) BM.AC + CN.AB + AI² = AB.AC

Lời giải:

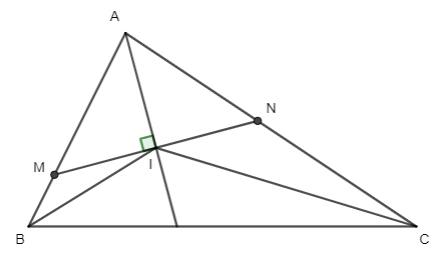
a) Xét tam giác AIM vuông tại I có: $\widehat{AMI}=90°-\frac{1}{2}\widehat{A}=\frac{1}{2}\left(180°-\widehat{A}\right)=\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\Rightarrow \widehat{BMI}=180°-\widehat{AMI}=180°-\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

Xét tam giác BIC, có: $\widehat{BIC}=180°-\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\Rightarrow \widehat{BMI}=\widehat{BIC}$

Xét ∆BMI và ∆BIC, có:

$\widehat{BMI}=\widehat{BIC}$ (cmt)

$\widehat{MBI}=\widehat{IBC}$

⇒ ∆BMI  ̴ ∆BIC (g – g)

$\Rightarrow \frac{BM}{BI}=\frac{BI}{BC}\iff B{I}^2=BM.BC$

Chứng minh tương tự ta có ∆CNI  ̴ ∆CIB (g – g)

$\Rightarrow \frac{CN}{CI}=\frac{CI}{CB}\iff C{I}^2=CN.CB$

$\Rightarrow \frac{B{I}^2}{C{I}^2}=\frac{BM}{CN}$.

b) Từ cm trên suy ra :△BMI ∼ △INC

$\Rightarrow \frac{BM}{IN}+\frac{MI}{NC}$

⇒ BM.CN = MI.NI

ta có : △AMN là tam giác cân

⇒ MI = NI

⇒ BM.CN = IM²

ta lại có : △AIM vuông

⇒ IM² = AM² – AI²

⇒ BM.CN = AM² – AI²

= AM.AN – AI² = (AB − BM)(AC − CN) – AI²

= AB.AC − AB.CN − BM.AC + BM.CN – AI²

⇒ BM.AC + CN.AB + AI² = AB.AC.

Câu 20: Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD. Chứng minh góc AMN = 90°

Cho hình vuông ABCD. O là giao điểm 2 đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB, CD.
a) Chứng minh góc AMN = 90°
b) A, M, N, D cùng thuộc 1 đường tròn
c) So sánh AN với MD

Lời giải:

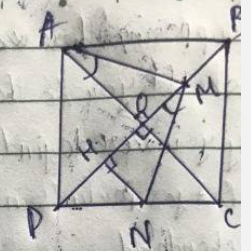
a) Kẻ NH vuông góc với DO

Ta có ABCD là hình vuông $\Rightarrow AC\perp BD$

Mà N là trung điểm DC, $NH\perp DO\Rightarrow NH//OC$

Suy ra NH là đường trung bình

Mà M là trung điểm OB (gt)

Suy ra H là trung điểm OD, $NH=\frac{1}{2}OC=OM$

Suy ra HM = OA

Xét tam giác OMA và tam giác HNM có:

$\widehat{H}=\widehat{O}=90°$

NH = MO

HM = OA

$\Rightarrow \Delta OMA=\Delta HNM\left(c.g.c\right)$

$\Rightarrow \widehat{OAM}=\widehat{HMN}$

$\Rightarrow \widehat{AMN}=\widehat{AMO}+\widehat{HMN}=\widehat{AMO}+\widehat{OAM}=90°$ (đpcm).

b) Gọi I là trung điểm của AN

Tam giác AMN vuông tại M $\Rightarrow MI=\frac{1}{2}AN=AI$

Tam giác ADN vuông tại D $\Rightarrow DI=\frac{1}{2}AN=AI$

Suy ra IA = IM = IN = ID

Suy ra 4 điểm A, M, N, D cùng thuộc đường tròn tâm I, bán kính IA.

c) Xét đường tròn ngoài tiếp tứ giác AMND có AN là dường kính và DM là dây nên AN > DM.

Câu 21: Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng $2\sqrt{5}$

A. m = 2

B. $\left[\begin{array}{c}m=-2\\ m=\frac{1}{2}\end{array}\right.$

C. $m=-\frac{1}{2}$

D.  Không tồn tại m.

Lời giải:

$d\left(A;\Delta \right)=\frac{\left|-m+2-m+4\right|}{\sqrt{m^2+1}}=2\sqrt{5}$

$\iff \left|m-3\right|=\sqrt{5}.\sqrt{m^2+1}$
⇔ 4m² + 6m – 4 = 0

$\iff \left[\begin{array}{c}m=-2\\ m=\frac{1}{2}\end{array}\right.$

Câu 22: Tìm tất cả các giá trị thực của tham số m để hàm số $y=x^3-3m{x}^2+3\left(m^2-1\right)x-m^3+m$ có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng $\sqrt{2}$ lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O

A. $m=-3-2\sqrt{2}$ hoặc m = - 1

B. $m=-3+2\sqrt{2}$ hoặc m = - 1

C. $m=-3+2\sqrt{2}$ hoặc $m=-3-2\sqrt{2}$

D. $m=-3+2\sqrt{2}$

Lời giải:

Chọn C

Ta có $y\text{'}=3x^2-6mx+3\left(m^2-1\right)$

Hàm số (1) có cực trị thì PT y' = 0 có 2 nghiệm phân biệt

⇔ x² - 2mx + m² – 1 = 0 có 2 nhiệm phân biệt

$\iff \Delta =1>\mathrm{0,}\forall m$

Khi đó, điểm cực đại A(m - 1; 2 - 2m) và điểm cực tiểu B (m + 1; - 2m)

Ta có $OA=\sqrt{2}OB\iff m^2+6m+1=0$

$\iff \left[\begin{array}{c}m=-3+2\sqrt{2}\\ m=-3-2\sqrt{2}\end{array}\right.$

Câu 23: Có tam giác ABC vuông tại A đg cao AH, E, F lần lượt là hình chiếu của H lên AB, AC. CM: BE.AC + CF. AB = AH. BC

Lời giải:

BE.AC + CF.AB

$$\begin{gathered} =\frac{H{B}^2}{AB}.AC+\frac{H{C}^2}{AC}.AB \\ =\frac{H{B}^2.AC}{AB}+\frac{H{C}^2.AB}{AC} \\ =\frac{H{B}^2.A{C}^2+H{C}^2.A{B}^2}{AB.AC} \\ =\frac{H{B}^2.HC.BC+H{C}^2.BH.BC}{AB.AC} \\ =\frac{BC.BH.CH\left(HB+HC\right)}{AH.BC} \\ =\frac{A{H}^2.BC}{AH}=AH.BC \end{gathered}$$

Câu 24: Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC.

Chứng minh rằng: AE. AB = AF. AC

Lời giải:

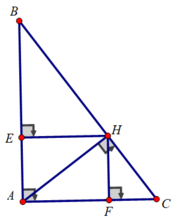
Xét tam giác ABH vuông tại H có HE là đường cao

⇒ AE.AB = AH2 (1)

Xét tam giác AHC vuông tại H có HF là đường cao

⇒ AF.AC = A H 2 (2)

Từ (1) và (2) ⇒ AE.AB = AF.AC

Câu 25: Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 9 thì y = - 15

a) Tìm hệ số tỉ lệ nghịch của y đối với x

b) Hãy biểu diễn y theo x

c) Tính giá trị của y khi x = - 5, x = 18

Lời giải:

a) Gọi a là hệ số tỉ lệ

Khi x = 3, y = 8

$$\begin{gathered} \Rightarrow 8=\frac{a}{3} \\ \iff a=24 \end{gathered}$$

Vậy hệ số tỉ lệ là 24

b) Ta có hệ số tỉ lệ k = 24 nên $y=\frac{24}{x}$.

c) Khi $x=-5\Rightarrow y=\frac{24}{-5}=-\frac{24}{5}$.

Khi $x=18\Rightarrow y=\frac{24}{18}=\frac{4}{3}$.

Câu 26: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 10 thì y = 5 vậy khi x = - 5 thì giá trị của y bằng bao nhiêu?

Lời giải:

Theo bài ra ta có: x và y là hai đại lượng tỉ lệ thuận.

⇒ y = k.x

Khi x = 10 thì y = 5

⇒ 5 = k.10

$\Rightarrow k=\frac{1}{2}$

$\Rightarrow y=\frac{1}{2}.x$

khi $x=-5\Rightarrow y=\frac{1}{2}.\left(-5\right)=-\mathrm{2,5}$.

Câu 27: Giải các phương trình sau

a) $x^2-6x+\sqrt{x^2-6x+7}=5$

b) $\sqrt{x+1}+\sqrt{x+6}=5$

c) $\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=4$

Lời giải:

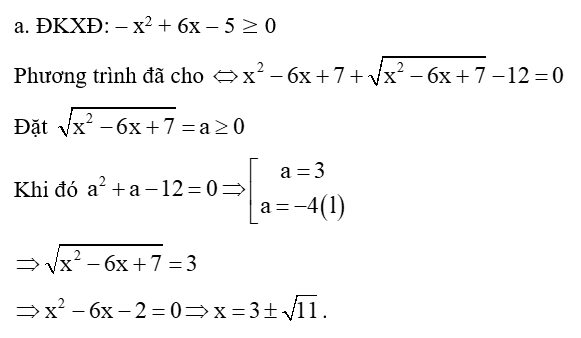
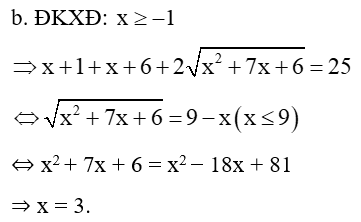
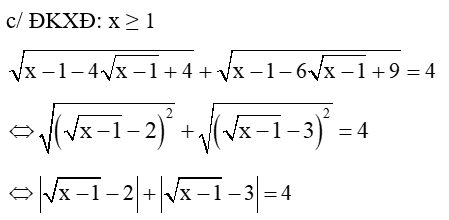
Chia 3 trường hợp: 1 ≤  x ≤ 5; x ≥ 10; 5 < x < 10 để phá trị tuyệt đối và giải bình thường.

Câu 28: Tìm các cặp số nguyên x,y thỏa mãn x³ – 6x² + 12x = y³ + 27

Lời giải:

Ta có  (x − 2)³ = x³ − 6x² + 12x – 8 > x³ − 6x² + 12x – 27 = y³

Ta có 6x² − 12x + 27 > 0 với moi x

⇒ −6x² + 12x – 27 < 0

⇒ y³ > x³

mà x y nguyên nên y³  nguyên  ⇒ y³ = (x − 1)³.

Câu 29: Tính $\frac{x^2-6x+9}{x^2-3x+9}.\frac{x^3+27}{3x-9}$.

Lời giải:

$\frac{x^2-6x+9}{x^2-3x+9}.\frac{x^3+27}{3x-9}$

$=\frac{{\left(x-3\right)}^2\left(x+3\right)\left(x^2-3x+9\right)}{\left(x^2-3x+9\right).3\left(x-3\right)}$

$=\frac{\left(x-3\right)\left(x+3\right)}{3}$

$=\frac{x^2-9}{3}$.

Câu 30: Phân tích thành nhân tử: x³ + y³ + z³ − 3xyz.

Lời giải:

Ta có x³ + y³ + z³ − 3xyz = (x + y)³ − 3xy(x + y) + z³ − 3xyz

= [(x + y)³ + z³] − [3xy(x + y) + 3xyz]

= (x + y + z)[(x + y)² − (x + y)z + z²] − 3xy(x + y + z)

= (x + y + z)(x² + 2xy + y² − xz − yz + z² − 3xy)

= (x + y + z)(x² + y² + z² − xy − xz − yz)

Câu 31: Bán kính của đường tròn nội tiếp tam giác đều cạnh a bằng:

Lời giải:

Diện tích tam giác đều cạnh a bằng:

$S=\frac{1}{2}.a.a.\sin 60°=\frac{a^2\sqrt{3}}{4}$

Lại có:

$S=pr\Rightarrow r=\frac{S}{p}=\frac{\frac{a^2\sqrt{3}}{4}}{\frac{3a}{2}}=\frac{a\sqrt{3}}{6}$

Vây bán kính của đường tròn nội tiếp tam giác đều cạnh a bằng $\frac{a\sqrt{3}}{6}$ .

Câu 32: Phân tích đa thức thành nhân tử: 

A = (x + 2)(x + 3)(x + 4)(x + 5) − 24

Lời giải:

A = (x + 2)(x + 3)(x + 4)(x + 5) − 24

= (x + 2)(x + 5)(x + 3)(x + 4) − 24

= (x² + 7x + 10)(x² + 7x + 12) – 24.

Đặt a = x² + 7x + 11. Thay vào A, ta được:

A = (a − 1)(a + 1) − 24 = a² − 25 = (a − 5)(a + 5) (2)

Thế a = x² + 7x + 11 vào (2), ta được:

A = (x² + 7x + 11 − 5)( x² + 7x + 11 + 5)

= (x² + 7x + 6)( x² + 7x + 16).

Câu 33: Khai triển (a + b + c)²; (a + b − c)²; (a − b − c)².

Lời giải:

+) (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

+) (a + b − c)² = a² + b² + c² + 2ab − 2bc − 2ca

+) (a − b − c)² = a² + b² + c² − 2ab + 2bc − 2ca.

Câu 34: Tính tổng:

F = 1² + 2² + 3² + … + n².

Lời giải:

F = 1² + 2² + 3² + … + n²

= 1 + (1 + 1).2 + (1 + 2).3 + … + (1 + n − 1).n

= 1 + 2 + 1.2 + 3 + 2.3 + … + n + (n − 1).n

= (1 + 2 + 3 + … + n) + [1.2 + 2.3 + … + (n − 1).n]

Đặt A = 1 + 2 + 3 + … + n

$\Rightarrow A=\frac{\left(n+1\right).n}{2}$ (1)

Đặt B = 1.2 + 2.3 + … + (n − 1).n

Þ 3B = 1.2.3 + 2.3.3 + … + (n − 1).n.3

3B = 1.2.3 + 2.3.(4 − 1) + … + (n − 1).n.[(n + 1) − (n − 2)]

3B = 1.2.3 + 2.3.4 − 1.2.3 + … + (n − 1).n.(n + 1) − (n − 2).(n − 1).n

3B = (n − 1).n.(n + 1)

$\Rightarrow B=\frac{\left(n-1\right).n.\left(n+1\right)}{3}$ (2)

Từ (1) và (2) $\Rightarrow F=\frac{\left(n+1\right).n}{2}+\frac{\left(n-1\right).n.\left(n+1\right)}{3}$ .

Câu 35: Phân tích đa thức x⁵ − 3x⁴ + 3x³ − x² thành nhân tử.

Lời giải:

x⁵ − 3x⁴ + 3x³ − x²

= x²(x³ − 3x² + 3x − 1)

= x²(x − 1)³.

Câu 36: Một bạn sinh viên tham gia một kì thi qua 3 vòng thi. Xác suất để bạn sinh viên này thi đậu vòng 1 là 0,5. Nếu qua khỏi vòng 1 thì xác suất để bạn này thi đậu ở vòng 2 là 0,6. Nếu đã vượt qua được hai vòng trước đó thì xác suất để bạn ấy thi đậu vòng 3 là 0,7. Tính xác sất để bạn sinh viên này thi đậu tất cả các vòng thi.

Lời giải:

Gọi A, B, C lần lượt là biến cố bạn sinh viên này thi đậu ở vòng 1, 2, 3. Khi đó bạn này thi đậu tất cả các vòng khi tất cả các biến cố này đồng thời xảy ra, và áp dụng công thức nhân xác suất thứ hai ta có:

P (ABC) = P (A).P (B/A).P (C/AB) = 0,5.0,6.0,7 = 0,21.

Câu 37: Trong tập số tự nhiên, tìm các ước của 4, của 6, của 9, của 13 và của 1.

Lời giải:

 - Lần lượt chia 4 cho 1; 2; 3; 4 ta thấy 4 chia hết cho 1; 2; 4

Vậy Ư(4) = {1; 2; 4}

- Lần lượt chia 6 cho 1; 2; 3; 4; 5; 6 ta thấy 6 chia hết 1; 2; 3; 6.

Vậy Ư(6) = {1; 2; 3; 6}.

- Lần lượt chia 9 cho 1; 2; 3; 4; 5; 6; 7; 8; 9 ta thấy 9 chia hết cho 1; 3; 9

Vậy Ư(9) = {1; 3; 9}.

- Lần lượt chia 13 cho 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13. Ta thấy 13 chia hết cho 1 và 13.

Vậy Ư(13) = {1; 13}.

Câu 38: Phân tích đa thức sau thành nhân tử x³ – 7x – 6 .

Lời giải:

x³ – 7x – 6 = x³ + 1 – 7x – 7

= (x + 1)( x² – x + 1) – 7(x + 1)

= (x + 1) (x² – x + 1 – 7)

= (x + 1)( x² – x – 6)

= (x + 1)( x² + 2x – 3x – 6)

= (x + 1)[x .(x + 2) – 3(x + 2)]

= (x + 1)(x + 2)(x – 3).

Câu 39: Cho hai tập khác rỗng: A = (m – 1; 4], B =  (−2; 2m + 2); với m ∈ ℝ. Giá trị m để A ∩ B ⊂ (−1; 3) là:

A. m > 0;

B. $m<\frac{1}{2}$ ;

C. $0<m<\frac{1}{2}$ ;

D. $0\le m\le \frac{1}{2}$ .

Lời giải:

Đáp án đúng là: D.

Điều kiện để tồn tại tập hợp A, B là:

$$\begin{gathered} \left\{\begin{array}{l}m-1<4\\ -2<2m+2\end{array}\right. \\ \iff \left\{\begin{array}{l}m<5\\ m>-2\end{array}\right. \end{gathered}$$

$\iff -2<m<5$ (*)

A ∩ B ⊂ (−1; 3)

$$\begin{gathered} \iff \left\{\begin{array}{l}m-1\ge -1\\ 2m+2\le 3\end{array}\right. \\ \iff \left\{\begin{array}{l}m\ge 0\\ m\le \frac{1}{2}\end{array}\right. \\ \iff 0\le m\le \frac{1}{2} \end{gathered}$$

Kết hợp với điều kiện (*) ta có $0\le m\le \frac{1}{2}$  là giá trị cần tìm.

Câu 40: Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BN và CM giao nhau tại H, AH cắt BC tại K.

a) Chứng minh: $AK\perp BC$ .

b) Chứng minh: AM.AB = AN.AC

c) Chứng minh: MH là phân giác góc NMK.

d) MN và BC cắt nhau tại S. Chứng minh: SB.SC = SK. SO

Lời giải:

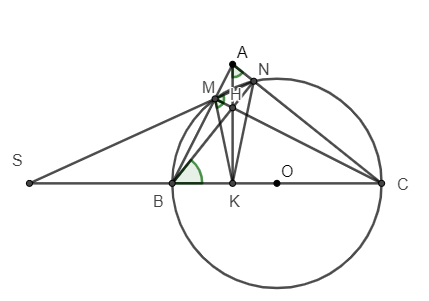
a) Ta có: BC là đường kính của (O) suy ra $CM\perp AB$ , $BN\perp AC$ .

Mà $BN\cap CM=H$ suy ra H là trực tâm tam giác $\Delta ABC$

$\Rightarrow AK\perp BC$ (đpcm)

b) Ta có: $CM\perp AB$ , $BN\perp AC$

$\Rightarrow \cos \widehat{A}=\frac{AM}{AC}=\frac{AN}{AB}$ (đpcm)

c) Ta có:

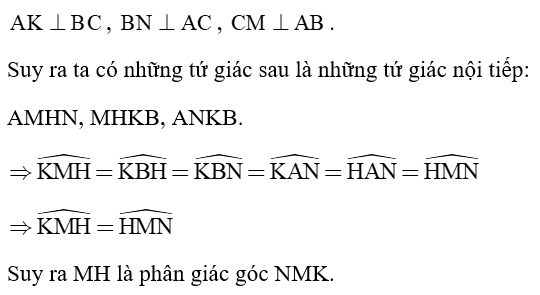
d) Ta có:

Câu 41: Phân tích đa thức x⁴ + 4 thành nhân tử.

Lời giải:

x⁴ + 4

= x⁴ + 4 + 4x² – 4x²

= (x⁴ + 4x² + 4) – (2x)²

= (x² + 2)² – (2x)²

=(x² + 2 – 2x)(x² + 2 + 2x)

Câu 42: Giải phương trình (x – 1)(x – 2)(x – 3)(x – 4) = 24

A. S = {0; −5};

B. S = {0; 5};

C. S = {5};

S = {0}.

Lời giải:

Đáp án đúng là

(x – 1)(x – 2)(x – 3)(x – 4) = 24

$\iff$(x – 1)(x – 4)(x – 2)(x – 3) = 24

$\iff$(x² – 5x + 4)(x² – 5x + 6) = 24

Đặt x² – 5x + 4 = t khi đó ta có:

t(t + 2) = 24

$\iff$t² + 2t – 24 = 0 (*)

a = 1; b’  = 1; c = −24

∆’ = 1 + 24 = 25 > 0; $\sqrt{\Delta \text{'}}=5$

Khi đó phương trình (*) có 2 nghiệm phân biệt là:

t₁ = −1 + 5 = 4; t₂ = −1 – 5 = −6

+) TH1: t₁ = 4 ta có:

x² – 5x + 4 = 4

x² – 5x = 0

x(x – 5) = 0

+) TH2 t₂ = −6 ta có:

x² – 5x + 4 = −6

x² – 5x  + 10 = 0

∆ = ( −5)² – 4.10 = −15 < 0 ( phương trình vô nghiệm)

Vậy S = {0; 5}.

Câu 43: Tìm bất phương trình bậc nhất hai ẩn trong các bất phương trình sau và chỉ ra một nghiệm của bất phương trình bậc nhất hai ẩn đó:

a) 5x + 3y < 20;

b) $3x-\frac{5}{y}>2$ .

Lời giải:

Bất phương trình bậc nhất 2 ẩn là: 5x + 3y < 20.

Chọn x₀ = 1 và y₀ = 1 ta có: 5. 1 + 3. 1 = 8 < 20.

Vậy (1; 1) là một nghiệm của bất phương trình bậc nhất hai ẩn 5x + 3y < 20.

Câu 44: Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.

a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.

b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Lời giải:

a) Với x = 1, y = 2, thay vào bất phương trình ta có: 1 + 2.2 = 5 ≥ 0 (luôn đúng)

Suy ra (1; 2) là nghiệm của bất phương trình đã cho.

Với x = −2, y = 1, thay vào bất phương trình ta có: −2 + 2.1 = 0 ≥ 0 (luôn đúng)

Suy ra (−2; 1) là nghiệm của bất phương trình đã cho.

Với x = 7, y = −2, thay vào bất phương trình ta có: 7 + 2.(−2) = 3 ≥ 0 (luôn đúng)

Suy ra (7; −2) là nghiệm của bất phương trình đã cho.

b) Thay y = 0 vào bất phương trình đã cho ta được: x + 2.0 ≥ 0 ⇔ x ≥ 0.

Vậy với y = 0 thì có vô số giá trị của x mà x ≥ 0 thỏa mãn bất phương trình đã cho.

Câu 45: Phân tích x⁵ – x⁴ – x³ – x² – x – 2 thành nhân tử.

Lời giải:

x⁵ – x⁴ – x³ – x² – x – 2

= x⁵ – 2x⁴ + x³ – 2x³ + x² – 2x² + x – 2x – 2

= ( x⁵ – 2x⁴) + (x⁴ – 2x³) + (x³ – 2x²) + (x² – 2x) + (x – 2)

= x⁴(x – 2) + x³(x – 2) + x²(x – 2) + x(x – 2) + (x – 2)

= (x – 2)(x⁴ + x³ + x² + x + 1).

Câu 46: Hàm số y = sinx đồng biến trên khoảng nào sau đây?

A. $\left(7\pi ;\frac{15\pi }{2}\right)$ ;

B. $\left(-\frac{7\pi }{2};-3\pi \right)$ ;

C. $\left(\frac{19\pi }{2};10\pi \right)$ ;

D. $\left(-6\pi ;-5\pi \right)$ .

Lời giải:

Đáp án đúng là: C

Hàm số y = sinx đồng biến trên D khi y' = cosx > 0, ∀x ∈ D.

Lại có bất phương trình cos x > 0 có nghiệm: 

$x\in \left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$, k ∈ ℤ .

Với k = 5 thì $x\in \left(\frac{19\pi }{2};\frac{21\pi }{2}\right)$ .

Mà $\left(\frac{19\pi }{2};10\pi \right)\subset \left(\frac{19\pi }{2};\frac{21\pi }{2}\right)$ .

Do đó hàm số y = sin x đồng biến trên $\left(\frac{19\pi }{2};10\pi \right)$ .

Trên các đoạn $\left(7\pi ;\frac{15\pi }{2}\right);\left(\frac{-7\pi }{2};-3\pi \right);\left(-6\pi ;-5\pi \right)$

ta kiểm tra được cos x < 0.

Do đó hàm số y = sin x nghịch biến trên các khoảng này.

Câu 47: Phân tích thành nhân tử 

A = (a + b + c)³ – (a + b – c)³ – (b + c – a)³ – (c + a – b)³

Lời giải:

Đặt a + b – c = x; b + c – a = y; c + a – b = z.

Khi đó ta có:

x + y + z = a + b + c.

Áp dụng hằng đẳng thức: (x + y + z)³ = x³ + y³ + z³ + 3(x + y)(y + z)(z + x) ta có:

A = (x + y + z)³ – x³ – y³ – z²

= x³ + y³ + z³ + 3(x + y)(y + z)(z + x) – x³ – y³ – z²

= 3(x + y)(y + z)(z + x)

= 3(a + b – c + b + c – a)(b + c – a + c + a – b)(c + a – b + a + b – c)

= 3. 2b. 2c. 2a

= 24abc.

Câu 48: Tìm GTNN của biểu thức C = x² – 4xy + 5y² + 10x – 22y + 28

Lời giải:

C = x² – 4xy + 5y² + 10x – 22y + 28

= (x² – 4xy + 4y²) + (10x – 20y) + (y² – 2y + 1) + 27

= (x – 2y)² + 10(x – 2y) + (y – 1)² + 27

= (x – 2y)² + 2. (x – 2y). 5 + 5² + (y – 1)² + 2

= (x – 2y + 5)² + (y – 1)² + 2

Vì (x – 2y + 5)² ≥ 0 với mọi x; y ∈ ℝ.

Và (y – 1)² ≥ 0 với mọi y ∈ ℝ.

Nên (x – 2y + 5)² + (y – 1)² + 2 ≥ 2 với mọi x; y ∈ ℝ.

Hay C ≥ 2 với mọi x; y ∈ ℝ.

Dấu “=” xảy ra khi và chỉ khi:

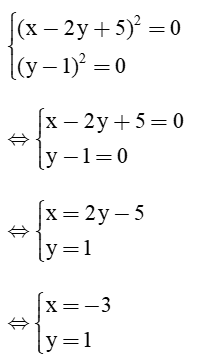
Vậy C_min = 2 khi x = −3 và y = 1.

Câu 49: Ba bạn A,B,C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1; 17]. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng:

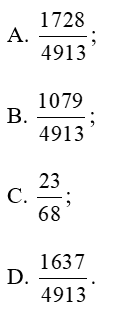
Lời giải:

Đáp án đúng là: D.

Không gian mẫu có số phần tử là 17³ = 4913.

Lấy một số tự nhiên từ 1 đến 17 ta có các nhóm số sau:

+) Số chia hết cho 3: có 5 số thuộc tập {3; 6; 9; 12; 15}.

+) Số chia cho 3 dư 1: có 6 số thuộc tập {1; 4; 7; 10; 13; 16}.

+) Số chia cho 3 dư 2: có 6 số thuộc tập {2; 5; 8; 11; 14; 17}.

Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1; 17] thỏa mãn ba số đó có tổng chia hết cho 3 thì các khả năng xảy ra như sau:

TH1: Ba số đều chia hết cho 3 có 5³ = 125 cách.

TH2: Ba số đều chia cho 3 dư 1 có 6³ = 216 cách.

TH3: Ba số đều chia cho 3 dư 2 có  6³ = 216 cách.

TH4: Một số chia hết cho 3, một số chia cho 3 dư 1, chia cho 3 dư 2 có

5.6.3! = 1080 cách.

Vậy xác suất cần tìm là $\frac{125+216+216+1080}{4913}=\frac{1637}{4913}$ .

Câu 50: Một lớp có 45 học sinh. Mỗi em đều đăng ký chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng ký môn bóng đá, 15 em đăng ký môn bóng chuyền. Hỏi có bao nhiêu em đăng ký cả hai môn bóng đá và bóng chuyền?

A. 30;

B. 10;

C. 5;

D. 25.

Lời giải:

Đáp án đúng là: C.

Gọi A tập các học sinh chơi bóng đá và B là tập các học sinh chơi bóng chuyền

Suy ra |A| = 35, |B| = 15.

Tập các học sinh của lớp là A ∪ B, |A ∪ B| = 45

Tập các học sinh đăng kí cả hai môn là A ∩ B

Ta có |A ∪ B| = |A| + |B| − |A ∩ B| =  45

 35 + 15 − |A ∩ B| = 45

|A ∩ B| = 5

Vậy số học sinh đăng kí cả hai môn bóng đá và bóng chuyền là 5 học sinh.

Câu 51: Phân tích đa thức x² – 6x + 8 thành nhân tử ta được:

A. (x – 4)(x – 2);

B. (x – 4)(x + 2);

C. (x + 4)(x + 2);

D. (x – 4)(2 – x).

Lời giải:

Đáp án đúng là: A.

Ta có x² – 6x + 8

= x² – 4x – 2x + 8

= x(x – 4) – 2(x – 4)

= (x – 4)(x – 2).

Câu 52: Tìm x:

a) 8x³ – 12x² + 6x – 1 = 0;

b) (4x – 3)² – 3x(3 – 4x) = 0.

Lời giải:

a) 8x³ – 12x² + 6x – 1 = 0

$\iff$(2x)³ – 3.(2x)².1 + 3. 2x. 1² - 1³ = 0

$\iff$(2x – 1)³ = 0

$\iff$2x – 1 = 0

$\iff x=\frac{1}{2}$.

Vậy $x=\frac{1}{2}$ .

b)

$\iff$(4x – 3)² – 3x(3 – 4x) = 0

$\iff$(4x – 3)² + 3x(4x – 3) = 0

$\iff$(4x – 3)(4x – 3 + 3x) = 0

$\iff$(4x – 3)(7x – 3) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}4x-3=0\\ 7x-3=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=\frac{3}{4}\\ x=\frac{3}{7}\end{array}\right. \end{gathered}$$

Vậy $x=\frac{3}{4}$  hoặc $x=\frac{3}{7}$ .

Câu 53: Nêu công thức xác suất đầy đủ.

Lời giải:

Cho không gian mẫu $\Omega$  và A₁, A₂, …. A_n, B là các biến cố.

Các biến cố A₁, A₂, …. A_n được gọi là một hệ biến cố đầy đủ nếu chúng thỏa mãn 2 điều kiện:

$A_1\cup A_2\cup \mathrm{...}\cup A_n=\Omega$

$A_i\cap A_j=\varnothing$ với mọi i ≠ j và i, j ∈ {1, 2, …,n}

Khi đó ta có:

$P\left(B\right)=\sum _{i=1}^{n}P\left(A_i\right)P(B/A_i)$

Các xác suất P(A₁); P(A₂);…; P(A_n) thường được gọi là các xác suất của các giả thiết (hay các xác suất tiên nghiệm) và công thức trên được gọi là công thức xác suất đầy đủ.

Câu 54: Tìm GTLN của biểu thức

A = 5 – 8x – x².

Lời giải:

A = 5 – 8x – x²

= −(x² + 8x – 5)

= −(x² + 2.x.4 + 16 – 21)

= −(x + 4)² + 21

Ta có với mọi x ∈ ℝ (x + 4)² ≥ 0 ⇔ −(x + 4)² + 21 ≤ 21.

Vậy A_max = 21 khi x = −4.

Câu 55: Tìm số nguyên dương n để n⁵ + 1 chia hết cho n³ + 1.

Lời giải:

Ta có:

n⁵ + 1 = n²(n³ + 1) – n² + 1

Để A chia hết cho n³ + 1 thì số dư của phép chia bằng 0

(n⁵ + 1 chia cho n³ + 1 được thương là n² và số dư là 1 – n²)

Suy ra ta có: 1 – n² = 0 $\iff \left[\begin{array}{l}n=1\\ n=-1\end{array}\right.$

Vì n là số nguyên dương nên ta có n = 1 thỏa mãn yêu cầu bài toán.

Vậy có duy nhất một giá trị thỏa mãn yêu cầu bài toán là n = 1.

Câu 56: Phân tích đa thức thành nhân tử.

x⁵ + x⁴ + 1

Lời giải:

a) x⁵ + x⁴ + 1

= x⁵ + x⁴ + x² – x² + 1

= x²(x³ – 1) + (x⁴ + x² + 1)

= x²(x³ – 1) + ( x⁴ + x³ – x³ + x² – x² + x² – x + x + 1)

= x²(x³ – 1) + [(x⁴ + x³ + x²) – (x³ + x² + x) + ( x² + x + 1)]

= x²(x³ – 1) + [x²(x² + x + 1) – x(x² + x + 1) + (x² + x + 1)]

= x²(x – 1)(x² + x + 1) + (x² + x + 1)(x² – x + 1)

= (x² + x + 1)[x²(x – 1) + x² – x+ 1]

= (x² + x + 1)(x³ – x² + x² – x + 1)

= ( x² + x + 1)(x³ – x + 1)

Câu 57: Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.

Lời giải:

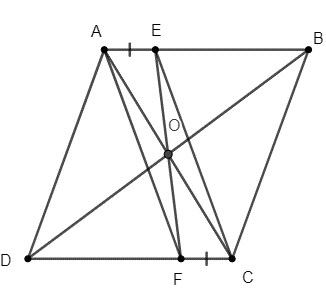
Vì ABCD là hình bình hành

AB//CD hay AE//CF.

Lại có: AE = CF (gt),

Suy ra AECF là hình bình hành.

AC, EF cắt nhau tại trung điểm mỗi đường.

Hay O ∈ AC; O ∈ CF (1).

Mà AC và BD cũng cắt nhau tại trung điểm mỗi đường ( do ABCD là hình bình hành).

O ∈ AC; O ∈ BD (2).

Từ (1) và (2) suy ra ba đường thẳng AC, BD, EF đồng quy (đpcm).

Câu 58: Số các giá trị nguyên của tham số m để hàm số y = x³ – mx² + (m² – 2m)x  có cực tiểu tại x = 0 là:

A. vô số;

B. 3;

C. 2;

D. 4.

Lời giải:

Đáp án đúng là: A

y’ = 3x² – 2mx + (m² – 2m)

y’ = 0 $\iff$ 3x² – 2mx + (m² – 2m) = 0 (*)

Cực trị của hàm số ban đầu là nghiệm của phương trình (*):

f(x) = 3x² – 2mx + (m² – 2m) = 0

Hàm số đạt cực tiểu tại x = 0 $\iff$  f’(0) > 0

Ta có: f’(x) = 6x – 2m

   f’(0) = −2m > 0 $\iff$ m < 0

Vậy có vô số giá trị m thỏa mãn yêu cầu bài toán.

Câu 59: Cho tập A ={1; 2} và B ={1; 2; 3; 4; 5}. Có tất cả bao nhiêu tập X thỏa mãn (A ⊂ X ⊂ B).

A. 5;

B. 6;

C. 7;

D. 8.

Lời giải:

Đáp án đúng là: D

Các tập X cần tìm là: {1; 2}; {1; 2; 3}; {1; 2; 4}; {1; 2; 5}; {1; 2; 3; 4}; {1; 2; 3;5}; {1; 2; 4; 5}; {1; 2; 3; 4; 5}.

Câu 60: Đổi biến u = sinx thì $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\sin }^{4}x.\cos xdx$  thành:

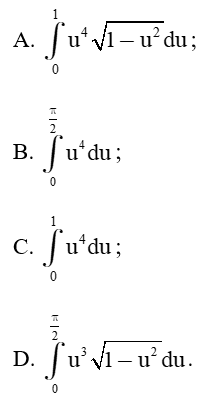
Lời giải:

Đáp án đúng là: C.

u(0) = sin0 = 0.

$u\left(\frac{\pi }{2}\right)=\sin \frac{\pi }{2}=1$

Sin⁴x.cosxdx = sin⁴x d(sinx) = u⁴du

Vậy $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\sin }^{4}x.\cos xdx=\underset{0}{\overset{1}{\int }}{u}^{4}du$ .

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 2)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 3)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 4)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 5)

1500 câu hỏi ôn tập môn Toán có đáp án (Phần 6)