1500 câu hỏi ôn tập môn Toán có đáp án (Phần 49)

1500 câu hỏi ôn tập Toán (Phần 49)

Câu 1: Kết quả phép tính 1 + 3 + 5 + ... + 19 – 2 – 4 – … – 18 bằng bao nhiêu

Lời giải:

1 + 3 + 5 + ... + 19 – 2 – 4 – … – 18

= (1 + 3 + 5 + ... + 19) – (2 + 4 +… + 18)

= $\left(\frac{19-1}{2}+1\right)\frac{\left(19+1\right)}{2}$ – $\left(\frac{18-2}{2}+1\right)\frac{\left(18+2\right)}{2}$

= 100 – 90

= 10.

Câu 2: Hình bình hành ABCD có độ dài đáy DC là $\frac{1}{4}$  m, chiều cao AH là 2 dm 4 cm. Tính diện tích hình đó dưới dạng dm.

Lời giải:

Đổi 2 dm 4 cm = 24 cm

$\frac{1}{4}$ m = 25 cm.

Diện tích hình bình hành là :

24 . 25 = 600 (cm²).

Đổi 600 cm² = 6 dm².

Câu 3: Một hợp tác xã dự định trồng rau sạch trên diện tích là 1ha 422m². Người ta đã trồng được $\frac{4}{9}$  diện tích đó. Hỏi hợp tác xã còn lại bao nhiêu mét vuông chưa trồng rau?

Lời giải:

Đổi 1ha 422 m² = 10422 m²

Người ta đã trồng được số diện tích là:

10422 . $\frac{4}{9}$  = 4632 (m²)

Hợp tác xã đó còn lại số mét vuông chưa trồng rau là:

10 422 – 4632 = 5790 (m²)

Đáp số: 5790 m².

Câu 4: Một miếng đất hình chữ nhật có chiều dài là 64 m chiều rộng là 34 m.

a) Tính chu vi mảnh đất đó

b) Người ta giảm 8m chiều dài và tăng chiều rộng để miếng đất thành hình vuông, biết phần diện tích giảm theo chiều dài là 272 m². Tính phần diện tích tăng thêm theo chiều rộng?

Lời giải:

a) Diện tích mảnh đất lúc đầu là:

64 . 34 = 2176 (m²).

b) Diện tích mảnh đất khi bị giảm chiều dài và giữ nguyên chiều rộng là:

2176 – 272 = 1904 (m²).

Chiều dài khi bị giảm là:

1904 : 34 = 56 (m).

Nếu chiều rộng tăng lên và bớt chiều dài thì diện tích hình vuông là:

56 . 56 = 3136 (m²).

Phần diện tích tăng thêm theo chiều rộng là:

3136 – 2176 = 960 (m²).

Đáp số: 960 m².

Câu 5: Một tấm bìa hình vuông có cạnh $\frac{3}{8}$ m. Tính chu vi và diện tích tấm bìa đó.

Lời giải:

Đổi $\frac{3}{8}$ m = 0,375 m

Chu vi tấm bìa là:

4 . 0,375 = 1,5 (m).

Diện tích tấm bìa là:

0,375 . 0,375 = 0,140625 (m²).

Câu 6: Mội tổ có 8 công nhân làm trong 4 giờ được 120 sản phẩm. Hỏi 8 công nhân đó làm trong 3 giờ được bao nhiêu sản phẩm ? (Biết mức làm của mỗi người người như nhau).

Lời giải:

Số sản phẩm mỗi giờ làm được là:

120 : 4 = 30 (sản phẩm)

Trong 3 giờ làm được số sản phẩm là:

30 . 3 = 90 (sản phẩm).

Đáp số: 90 sản phẩm.

Câu 7: Một đơn vị bộ đội chuẩn bị đủ gạo cho 1200 người ăn trong 35 ngày, nhưng vì 480 người đến thêm nên số gạo đó chỉ đủ ăn trong bao nhiêu ngày?

Lời giải:

Sau khi 480 người đến thêm, tổng số người cần ăn:

1200 + 480 = 1680 (người)

Số gạo đó đủ ăn trong số ngày:

(35 . 1200) : 1680 = 25 (ngày)

Đáp số: 25 ngày.

Câu 8: Người ta lát sàn một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 4m bằng những mảnh gỗ hình chữ nhật có chiều dài 1m 20cm, chiều rộng 20cm. Hỏi cần bao nhiêu mảnh gỗ để lát kín sàn căn phòng đó?

Lời giải:

Đổi 11m 20cm = 1,2 m; 20cm = 0,2 m

Số hàng gỗ theo chiều dài của căn phòng là: 

6 : 1,2 = 5 (hàng)

Số hàng gỗ theo chiều rộng của căn phòng là:

4 : 0.2 = 20 (hàng)

Số miếng gỗ cần dùng là: 

5 . 20 = 100 (miếng gỗ).

Đáp số: 100 miếng gỗ.

Câu 9: Năm nay tuổi bố gấp 6 lần tuổi con, bốn năm sau tuổi bố gấp 4 lần tuổi con. Hỏi hiện tại bố bao nhiêu tuổi?

Lời giải:

Gọi tuổi con năm nay là a thì tuổi bố năm nay là 6a (a ≠ 0)

4 năm sau, tuổi bố là: 6a + 4

4 năm sau, tuổi con là a + 4

Ta có: 6a + 4 = 4 (a + 4)

6a + 4 = 4a + 16

2a = 12

a = 6

Vậy tuổi con năm nay là 6 thì tuổi bố năm nay là:

6 . 6 = 36 (tuổi).

Câu 10: Cho dãy số 2 , 6, 12 ,.. Số hạng thứ 6 của dãy số đã cho là bao nhiêu?

Lời giải:

Ta thấy:

2 = 1 . 2

6 = 2 . 3

12 = 3 . 4

Quy luật: mỗi số hạng thuộc dãy trên là tích của 2 số tự nhiên liên tiếp và thừa số thứ nhất của 2 số liên tiếp hơn kém nhau 1 đơn vị.

Vậy số hạng thứ 6 của dãy là: 6 . 7 = 42.

Câu 11: Tổng của hai số tự nhiên là 102. Nếu thêm chữ số 0 vào bên phải số bé rồi cộng với số lớn ta được tổng mới là 417. Tìm số lớn.

Lời giải:

Gọi a là số bé, b là số lớn, ta có:

a + b = 102

$\overline{a0}$ + b = 10a + b = 417

⇔10a + b – (a + b) = 315

⇔10a + b – a – b = 315

⇔ 9a = 315

⇔ a = 35

Suy ra: b = 102 – 35 = 67.

Vậy số lớn là 67.

Câu 12: Tìm a,b thuộc ℤ sao cho  a.b = a + b.

Lời giải:

Ta có: a.b = a + b

⇔ a.b – a = b 

⇔ a (b–1) = b

⇔ a = $\frac{b}{b-1}=1+\frac{1}{b-1}$

Vì a, b thuộc ℤ nên b – 1 ∈ Ư(1)

Suy ra: b – 1 = 1 hoặc b – 1 = –1

Với b – 1 = 1 hay b = 2, thì a = 2

Với b – 1 = – 1 hay b = 0, thì a = 0

Vậy (a; b) ∈ {(2; 2) , (0; 0)}.

Câu 13: Tổng của một số thập phân và một số tự nhiên bằng 105,6. Khi viết, bạn học sinh viết nhầm dấu phẩy của số thập phân sang bên trái 1 hàng nên cộng hai số được tổng bằng 84,36. Số thập phân ban đầu là?

Lời giải:

Gọi số tự nhiên bằng a

Số thập phân là x

Ta có:

a + x = 105,6 (1)

a + 0,1x = 84,36 (do dấu phẩy của số thập phân sang bên trái 1 hàng) (2)

Lấy (1) trừ (2) ta được:

a + x – a – 0,1x = 105,6 – 84,36

⇔ 0,9x = 21,24

⇔ x = 23,6.

Vậy số thập phân ban đầu là 23,6.

Câu 14: Tổng của một số thập phân và một số tự nhiên là 47,24. Tuy khi đặt tính , một bạn học sinh đã quên mất dấu phẩy ở số thập phân và đặt tính như cộng hai số tự nhiên nên được kết quả là 1259. Tìm số tự nhiên và số thập phân đó.

Lời giải:

Gọi số tự nhiên bằng a

Số thập phân là x

Ta có:

a + x = 47,24 (1)

a + 100x = 1259 (2)

Lấy (1) trừ (2) ta được:

a + x – a – 100x = 47,24 – 1259

– 99x = –1211,76

x = 12,24

Vậy số thập phân ban đầu là 12,24.

Câu 15: Chị Lan cắt một mảnh vải thành các mảnh nhỏ, mỗi mảnh nhỏ dài 12 dm, chị phải cắt tất cả 7 lần. Hỏi mảnh vải ban đầu của chị Lan dài bao nhiêu dm? (Biết mỗi mảnh vải sau khi cắt có kích thước như nhau).

Lời giải:

Chị Lan phải cắt 7 lần tức là mảnh vải ban đầu có 8 phần bằng nhau.

Mảnh vải ban đầu dài là:

12 . 8 = 96 (dm).

Câu 16: Cho dãy số: 7; 14; 21; 28; ........; ..........; 49; 56; 63; 70. Hai số còn thiếu là?

Lời giải:

Ta thấy ai số đứng liền nhau hơn kém nhau 7 đơn vị. Từ đó ta tìm được hai số cần điền.

Suy ra hai số đó là 35 và 42.

Câu 17: Nhà bếp dự trữ đủ lượng gạo cho 45 người ăn trong 6 ngày. Nếu có 54 người ăn số gạo đó thì số ngày ăn sẽ giảm đi bao nhiêu ngày (biết rằng suất ăn của mỗi người là như nhau).

Lời giải:

1 người ăn số gạo đó trong số ngày là :

45 . 6 = 270 ( ngày)

54 người ăn thì số gạo đó ăn trong số ngày là :

270 : 54 = 5 (ngày)

Số ngày giảm đi khi có 54 người ăn là :

6 – 5 = 1 ( ngày)

Đáp số : 1 ngày.

Câu 18: Nhà trường tổ chức cho học sinh khối 5 đi thăm quan. Nếu xếp 40 học sinh một xe thì cần 14 xe ô tô. Hỏi nếu xếp 35 học sinh thì cần bao nhiêu xe? (sức chở của mỗi xe là như nhau ?

Lời giải:

Số học sinh đi tham quan là:

40 . 14 = 560 (học sinh)

Nếu mỗi xe chở 35 học sinh thì cần số xe là:

560 : 35 = 16 (xe)

Đáp số: 16 xe.

Câu 19: Tìm một số biết rằng lấy số đó nhân với 6 rồi cộng với 6 cuối cùng chia cho 6 thì được 6.

Lời giải:

Gọi số cần tìm là A

Ta có:

(A . 6 + 6) : 6 = 6

A . 6 + 6 = 36

A . 6 = 30

A = 30 : 6

A = 5.

Vậy số cần tìm  là 5

Câu 20: Một căn phòng hình chữ nhật có chiều dài là 10m, chiều rộng bằng $\frac{3}{5}$  chiều dài. Người ta lát kín căn phòng bằng các viên gạch hoa hình vuông cạnh 4dm. Cần phải dùng ít nhất bao nhiêu viên gạch để lát kín nền căn phòng. (Diện tích phần mạch vữa không đáng kể).

Lời giải:

Chiều rộng căn phòng là:

10 .  $\frac{3}{5}$  = 6 (m)

Diện tích căn phòng là:

10 . 6 = 60 (m²)

Đổi 60 m² = 6000 dm²

Diện tích viên gạch là

4 . 4 = 16 (dm²)

Cần số viên gạch để lát kín nền căn phòng  là:

6000 : 16 = 375 (viên)

Đáp số: 375 viên.

Câu 21: Tính nhanh: 102 . 98

Lời giải:

102 . 98

= (100 + 2) . (100 – 2)

= 100 . 100 – 2 . 100 + 2 . 100 – 2 . 2

= 10000 – 4

= 9996.

Câu 22: Tìm số tự nhiên x; y biết (2x + 1)(y – 5) = 12.

Lời giải:

(2x + 1) (y – 5) = 1 . 12 = 2 . 6 = 3 . 4 = 4 . 3 = 6 . 2 = 12 . 1

Ta có bảng sau:

Vậy (x; y) ∈ {(0; 17) , (1; 9)}.

Câu 23: Tính bằng cách thuận tiện nhất:

100 – 99 + 98 – 97 + 96 – 95 + 94 – 93 + 92 – 91 + 90

Lời giải:

(100 – 99 )+ (98 – 97 )+ (96 – 95) +( 94 – 93) + (92 – 91) + 90

= 1 + 1 + 1 + 1 + 1 + 90

=1 . 5 + 90

= 5 + 90

= 95.

Câu 24: Khi nhân 1 số thập phân với 6,3 1 học sinh đã đặt các tích riêng thẳng cột nên được kết quả là 38,43. Tìm số thập phân đó?

Lời giải:

Do đặt tích riêng thẳng cột nên số đó được gấp lên:

6 + 3 = 9 lần

Số thập phân đó là:

38,43 : 9 = 4,27

Đáp số: 4,27.

Câu 25: Một mảnh vườn hình chữ nhật được vẽ trên bản đồ tỉ lệ 1 : 500 có chiều dài là 8 cm, chiều rộng 6 cm. Diện tích của mảnh vườn là bao nhiêu theo đơn vị ha ?

Lời giải:

Chiều dài thực tế của mảnh vường là:

8 . 500 = 4000 (cm).

Chiều rộng thực tế của mảnh vường là:

6 . 500 = 3000 (cm)

Diện tích của mảnh vườn là:

4000 . 3000 = 12000000 (cm²)

Đổi 12000000 cm² = 1200ha.

Câu 26: Tính tổng S = 1.2 + 2.3 + 3.4 +.... + 99.100.

Lời giải:

S = 1 . 2 + 2 . 3 + ... + 99 . 100

3S = 1 . 2 . 3 + 2 . 3 . (4 – 1) + ..... + 99 . 100 . (101 – 98)

3S = 1 . 2 . 3 + 2 . 3 . 4 – 1 . 2 . 3 + .... + 99 . 100 . 101 – 98 . 99 . 100

3S = 99 . 100 . 101

3S = 999900

S = 999900 : 3

S = 333300.

Câu 27: Một đám đất hình chữ nhật có chiều dài và chiều rộng là các số tự nhiên. Chiều dài gấp 3 lần chiều rộng. Có diện tích từ 60 đến 80 m². Tính chu vi đám đất.

Lời giải:

Vì chiều dài đám đất gấp 3 lần chiều rộng nên diện tích đám đất là số chia hết cho 3. Ta chia đám đất thành 3 hình vuông.

Từ  60 – 80 các số chia hết cho 3 là: 60, 63, 66, 69, 72, 75, 78.

Suy ra diện tích của mỗi hình vuông có thể là: 21, 22, 23, 24, 25, 26

Vì cạnh hình vuông cũng là chiều rộng của đám đất hình chữ nhật là một số tự nhiên nên diện tích hình vuông bằng 25.

Suy ra cạnh hình vuông hay chiều rộng đám đất là 5m để có 5 . 5 = 25 m

Chiều dài đám đất:

5 . 3 = 15 (m)

Chu vi hình chữ nhật:

(15 + 5) . 2 = 40 (m)

Đáp số: 40 m.

Câu 28: Phân tích đa thức thành nhân tử: 4xⁿ⁺² + 8xⁿ với n thuộc ℕ^*.

Lời giải:

4xⁿ⁺² + 8xⁿ = 4xⁿ (x² + 2).

Câu 29: Giải phương trình nghiệm nguyên: x² – y² + 2x – 4y – 10 = 0.

Lời giải:

x² – y² + 2x – 4y – 10 = 0

⇔ (x + 1)² – (y + 2)² = 7

Đặt (x + 1)² = m² và (y + 2)² = n²

Ta có: (x + 1)² – (y + 2)² = m² – n² = (m + n)(m – n) = 1 . 7

Vì m + n ≥ m – n nên m – n = 1 và m + n = 7

Suy ra: m = 4 và n = 3

Hay

$\left\{\begin{array}{l}{\left(x+1\right)}^2=4^2\\ {\left(y+2\right)}^2=3^2\end{array}\right.$⇒ $\left\{\begin{array}{l}x+1=4\\ y+2=3\end{array}\right.hay\left\{\begin{array}{l}x=\text{3}\\ y=1\end{array}\right.$ .

Câu 30: Chứng minh 3²⁰ đồng dư với 1 theo mod 100.

Lời giải:

Ta có: 3²⁰ chia 100 được 34867844 dư 1

1 chia 100 được 0 dư 1

Nên 3²⁰ ≡ 1 (mod 100).

Câu 31: Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng 4n + 1 hoặc 4n – 1.

Lời giải:

Giả sử số nguyên tố là p

Mọi số nguyên tố p lớn hơn 2 đều không chia hết cho 2

⇒ p có dạng 2n + 1 (k thuộc ℕ, k > 0)

Xét 2 trường hợp:

+ k chẵn (k = 2n) ⇒ p = 2k + 1 = 2.2n + 1 = 4n + 1

+ k lẻ (k = 2n – 1) ⇒ p = 2k + 1 = 2.(2n – 1) + 1 = 4n – 1

Vậy p luôn có dạng 4n + 1 hoặc 4n – 1.

Câu 32: Tìm n thuộc ℤ để (4n – 1) chia hết cho (n – 2).

Lời giải:

Ta có: $\frac{4n-1}{n-2}=4+\frac{7}{n-2}$

Để $\frac{4n-1}{n-2}$ ∈ ℤ thì 7 ⋮ (n–2)

Suy ra: n – 2 ∈ Ư(7)

n – 2 ∈ {–7; –1; 1; 7}

hay n ∈ {–5; 1; 3; 9}.

Câu 33: Chứng minh rằng B = 5⁰ + 5¹ + … + 5²⁰¹¹ chia hết cho 6.

Lời giải:

B = 5⁰ + 5¹ + … + 5²⁰¹¹

B = 1 + 5 + 5² + … + 5²⁰¹¹

B = (1 + 5) + (5² + 5³) + … + (5²⁰¹⁰ + 5²⁰¹¹)

B = 6 + 5²(1 + 5) + … + 5²⁰¹⁰(1 + 5)

B = 6 (1 + 5² + … + 5²⁰¹⁰)

Vì 6 (1 + 5² + … + 5²⁰¹⁰) chia hết cho 6 nên B chia hết cho 6.

Câu 34: Lớp 4a có 28 học sinh. Số học sinh nam nhiều hơn số học sinh nữ là 4 em. Hỏi lớp 4a có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?

Lời giải:

Số học sinh nữ là:

(28 – 4) : 2 = 12 (học sinh).

Số học sinh nam là:

28 – 12 = 16 (học sinh).

Đáp số: 12 học sinh nữ, 16 học sinh nam.

Câu 35: Một trường tiểu học trong học kì 1 thu được 2 tấn 750 kg giấy vụn, trong học kì 2 thu được 3 tấn 250 kg giấy vụn. Biết rằng cứ 2 tấn giấy vụn làm được 50000 cuốn vở. Hỏi từ số giấy vụn của trường có thể làm được bao nhiêu cuốn vở?

Lời giải:

Cả hai đợt thu gom được số giấy vụn là:

2 tấn 750 kg + 3 tấn 250kg = 5 tấn 1000kg = 6 tấn.

Cứ 2 tấn giấy vụn làm được 50000 cuốn vở, 6 tấn giấy vụn là được là:

 6 : 2 . 50000 = 150000 (cuốn vở)

Đáp số: 150 000 cuốn vở.

Câu 36: Một bếp ăn dự trữ gạo đủ cho 80 người ăn trong 27 ngày. Nay có thêm 40 mới chuyển đến. Hỏi số gạo đó đủ ăn trong bao nhiêu ngày?

Lời giải:

Số suất ăn hiện có là:

80 . 27 = 2160 (suất).

Lúc sau có tất cả số người ăn là:

80 + 40 = 120 (người).

120 người ăn trong số ngày là:

2160 : 120 = 18 (ngày).

Đáp số: 18 ngày.

Câu 37: Trên bãi cỏ có tất cả 25 con trâu và con bò số trâu bằng $\frac{1}{4}$  con bò hỏi trên bãi cát. Hỏi có bao nhiêu con trâu, bao nhiêu con bò?

Lời giải:

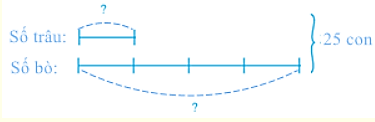
Số trâu là:

25 : (4 + 1)  = 5 (con).

Số bò là:

25 – 5 = 20 (con).

Đáp số: 5 con trâu, 20 con bò.

Câu 38: Tìm hai chữ số tận cùng của 3⁹⁹⁹.

Lời giải:

3⁹⁹⁹

= 3 . 3⁹⁹⁸

= 3 . (10 – 1)⁴⁹⁹

= 3 . (10⁴⁹⁹ – … + 499.10 – 1)

= 3. (BS 100 + 4989)

= ….67

Vậy hai chữ số tận cùng của 3⁹⁹⁹ là 67.

Câu 39: Chứng minh rằng A = n⁴ – 14n³ + 71n² – 154n + 120 chia hết cho 24.

Lời giải:

Để chứng minh A chia hết cho 24 tức là chứng minh A chia hết cho 2, 3 và 8.

Ta có:

A = n⁴ – 14n³ + 71n² – 154n + 120

A = n⁴ – 2n³ –12n³ + 24n² + 47n² – 94n–60n + 120

A = n³(n – 2) –12n² (n – 2) + 47n(n – 2) – 60(n – 2)

A= (n – 2)(n³ – 12n² + 47n – 60)

A = (n – 2)(n³ – 3n² – 9n² +27n + 20n  – 60)

A = (n – 2)(n – 3)[(n² – 4n) – (5n – 20)]

A = (n – 2)(n – 3)(n – 4)(n – 5)

Ta có: n – 2 và  n – 3 là hai số tự nhiên liên tiếp nên (n – 2)(n – 3) chia hết cho 2, suy ra A chia hết cho 2 (1)

n – 2; n – 3; n – 4 là ba số tự nhiên liên tiếp nên (n – 2)(n – 3)(n – 4) chia hết cho 2, suy ra A chia hết cho 3 (2)

n – 2; n – 3; n – 4; n – 5 là bốn số tự nhiên liên tiếp nên (n – 2)(n – 3)(n – 4)(n – 5)chia hết cho 4, suy ra A chia hết cho 4 (3)

Từ (1), (2) và (3) suy ra A chia hết cho 24.

Câu 40: Phân tích đa thức thành nhân tử: a⁴ + b⁴ + c⁴ – 2a²b² – 2b²c² – 2c²a².

Lời giải:

a⁴ + b⁴ + c⁴ – 2a²b² – 2b²c² – 2c²a²

= a⁴ + b⁴ + c⁴ + 2a²b²  – 4a²b² – 2b²c² – 2c²a²

= (a² + b²)² – 2 (a² + b²) c² + (c²)² – 4a²b²

= [(a² + b²) – c²]² – 4a²b²

= (a² + b²  – c²)² – (2ab)²

= (a² + b²  – c² – 2ab)( a² + b²  – c² + 2ab)

= [(a – b)² – c²][(a + b)² + c²]

= (a – b – c)(a – b + c)(a + b + c)(a + b – c).

Câu 41: Khẳng định sau đúng hay sai: 2, 3, 4 đôi một nguyên tố cùng nhau.

Lời giải:

Ta có:

2 = 2 . 1

3 = 1 . 3

4 = 2²

Xét 2 và 3 thấy ước chung lớn nhất của 2 và 3 là 1. Nên 2 và 3 là 2 số nguyên tố cùng nhau.

Xét 3 và 4 thấy ước chung lớn nhất của 3 và 4 khác 1. Nên 3 và 4 không nguyên tố cùng nhau.
Xét 2 và 4 thấy ước chung lớn nhất của 2 và 4 là 2. Nên 2 và 4 không nguyên tố cùng nhau.

Vậy khẳng định trên là sai.

Câu 42: Tìm x biết 3(2x – 1)² + 7(3y + 5)² = 0.

Lời giải:

Ta thấy: 3(2x – 1)² ≥ 0 với mọi x

7(3y + 5)² ≥ 0 với mọi y

Suy ra: 3(2x – 1)² + 7(3y + 5)² ≥ 0 với mọi x, y

Mà 3(2x – 1)² + 7(3y + 5)² = 0.

Dấu “=” xảy ra khi:

$\left\{\begin{array}{l}2x-1=0\\ 3y+5=0\end{array}\right.hay\left\{\begin{array}{l}x=\frac{1}{2}\\ y=\frac{-5}{3}\end{array}\right.$.

Câu 43: Tìm n biết (5ⁿ)² – 5ⁿ = 600.

Lời giải:

(5ⁿ)² – 5ⁿ = 600.

⇔ 5²ⁿ – 5ⁿ = 600

⇔ 5ⁿ (5² –  1) = 600

⇔ 5ⁿ = 25

⇔ n = 2.

Vậy n = 2.

Câu 44: Tính: A = 6 + 16 + 30 + 48 +... + 19600 + 19998.

Lời giải:

A = 6 + 16 + 30 + 48 +... + 19600 + 19998

A : 2 = 3 + 8 + 15 + 24  + . . . + 9800 + 9999

A : 2 = 1.3 + 2.4 + 3.5 + 4.6 + . . . + 98.100 + 99.101

A : 2 = 1.(1 + 2) + 2.(1 + 3) + 3.(1 + 4) + 4.(1 + 5) + . . . + 98.(1 + 99) + 99.(1 + 100)

A : 2 = 1 + 1.2 + 2 + 2.3 + 3 + 3.4 + 4 + 4.5 + . . . + 98 + 98.99 + 99 + 99.100

A : 2 = 1 + 2 + 3 + 4 + . . . + 199 + 1.2 + 2.3 + 3.4 + 4.5 + . . . + 98.99 + 99.100

A : 2 = 4950 + 333300

A : 2 = 338250

A = 676500.

Câu 45: Nêu 3 cách tính nhẩm 600 chia 12.

Lời giải:

Cách 1:

60 : 12 = 5

Suy ra: 600 : 12 =50

Cách 2:

6 : 12 = 1 : 2 = 0,5

600 = 6 . 100

Suy ra: 600 : 12 = 0,5 .100 =50

Cách 3:

12 . 1 = 12

12 . 2 = 24

...

12 . 5 = 60

Suy ra: 12 . 50 = 600

Câu 46: Chứng minh rằng A = 3⁰ + 3¹ + 3² + … + 3¹⁰ là số chẵn.

Lời giải:

A = 3⁰ + 3¹ + 3² + … + 3¹⁰

A = 1 + 3 + (3² + 3³) + … + (3⁹ + 3¹⁰)

A = 4 + 3²(1+3) + … + 3⁹ (1+3)

A = 4 (1 + 3² + … + 3⁹)

Ta thấy 4 (1 + 3² + … + 3⁹) chia hết cho 2, nên A chia hết cho 2.

Suy ra A là số chẵn.

Câu 47: Anh mua 1 quyển truyện và 1 cái bút hết tất cả 16 000 đồng. Biết rằng giá tiền 1 quyển truyện bằng $\frac{5}{3}$  giá tiền 1 cái bút. Hỏi Anh mua quyển truyện đó hết bao nhiêu tiền?

Lời giải:

Tổng số phần bằng nhau là:

5 + 3 = 8 (phần )

Anh mua quyển truyển đó hết số tiền là:

16000 : 8 . 5 = 10000 (đồng ).

Đáp số: 10 000 đồng.

Câu 48: Tính tổng C = 6¹ + 6³ + 6⁵.

Lời giải:

Ta có:

C = 6¹ + 6³ + 6⁵

C = 6¹(1 + 6² + 6⁴)

C = 6 . 1333

C = 7998.

Câu 49: Có bao nhiêu số có 3 chữ số khác nhau?

Lời giải:

Gọi số có 3 chữ số khác nhau là: $\overline{abc}$

Chữ số a có 9 cách chọn chữ số từ 1 đến 9 (khác chữ số 0),

Mỗi cách chọn của a có 9 cách chọn chữ số b từ 0 đến 9 (khác chữ số a)

Mỗi cách chọn chữ số b có 8 cách chọn chữ số c (khác chữ số a, chữ số b)

Suy ra có tất cả 9.9.8 = 648 số có 3 chữ số khác nhau.

Câu 50: Nêu điều kiện để số chia hết cho 25.

Lời giải:

Để số chia hết cho 25 thì số đó có 2 chữ số tận cùng chia hết cho 25.

Ví dụ: 12231225 chia hết cho 25 vì 25 chia hết cho 25.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác: