Cho ∆ADC vuông tại a có đường cao AH, AH = 3 cm. Trên nửa mặt phẳng

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 330 02/02/2024

Trang trước

Trang sau

Cho ∆ADC vuông tại a có đường cao AH, AH = 3 cm. Trên nửa mặt phẳng

Đề bài: Cho ∆ADC vuông tại a có đường cao AH, $\hat{D} = 65 °$ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song với AD, trên Cx lấy điểm B sao cho CB = DA. Tính khoảng cách từ B đến AD, độ dài đoạn BD và diện tích tam giác ABD.

Lời giải:

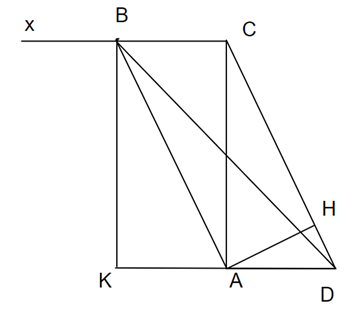
Tài liệu VietJack

Kẻ BK ⊥ AD

Xét ∆ADC $(\hat{A} = 90 °) : \hat{A D C} = 65 ° \Rightarrow \hat{A C D} = 25 °$

Khi đó: $C A = \frac{A H}{\sin \hat{C}} = \frac{3}{\sin 25 °}$

Dễ thấy BCAK là hình chữ nhật $\Rightarrow B K = A C = \frac{3}{\sin 25 °} (c m)$ và BC = AK

⟹ DA = AK (= BC) ⇒ DK = 2DA

Ta có: $D A = \frac{A H}{\sin \hat{C D A}} = \frac{3}{\sin 25 °} (c m)$

$D K = 2 D A = \frac{6}{\sin 25 °} (c m)$

Áp dụng định lí Pytago vào ∆BKD vuông tại K có $B K^{2} + K D^{2} = B D^{2}$

$\Leftrightarrow {(\frac{3}{\sin 25 °})}^{2} + {(\frac{6}{\sin 25 °})}^{2} = B D^{2} \Leftrightarrow B D^{2} = \frac{45}{\sin^{2} 25 °} \Leftrightarrow B D = \frac{3 \sqrt{5}}{\sin 25 °} (c m)$

Ta có

$S_{A B D} = S_{B K D} - S_{B A K} = \frac{B K . K D}{2} - \frac{A K . B K}{2} = \frac{B K}{2} (K D - A K) = \frac{B K . A D}{2} = \frac{\frac{3}{\sin 25 °} . \frac{3}{\sin 25 °}}{2} = \frac{18}{\sin 25 °} (c m^{2})$

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Cho tam giác ABC đều, cạnh AB = BC = AC = a = 6, kẻ đường cao từ A xuống cắt với BC...

Cho biểu thức P = ((x - 3cănx) / (x - 9) - 1) : ( (9 - x) / (x + cănx - 6...

Tìm x biết: x + 12 = – 5 – x...

Cho x/a + y/b + z/c = 1 và a/x + b/y + c/z = 0...

Cho hàm số y = (2x + 7) / (x + 2) có đồ thị (C...

Cho α là góc tù và sinα – cosα = 4/5. Giá trị của M = sinα – 2cosα là...

Giải phương trình: căn (4x^2 + 5x + 1) - 2căn(x^2 - x + 1) = 9x - 3...

Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a căn 2...

Cho ∆ADC vuông tại a có đường cao AH, AH = 3 cm. Trên nửa mặt phẳng...

Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h...

Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 60...

Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau...

Viết chương trình nhập số nguyên dương n. Kiểm tra n có phải là số nguyên tố...

Cho 2 điểm A(3; 0), B(0; 4). Phương trình đường tròn (C) có bán kính nhỏ nhất...

Giải phương trình: (x^2 - 5x + 1)(x^2 - 4) = 6(x - 1)^2...

Cho các số từ 1 đến 9. Hãy điền các số này vào các ô vuông, sao cho tổng của 3 ô...

Vẽ bản đồ tư duy hình vuông...

Vẽ bản đồ tư duy hình chữ nhật...

Tìm các số nguyên x, y thỏa mãn: 5x^2 - 4xy + y^2 = 169...

Cho tam giác ABC, tìm vị trí điểm I sao cho 2 vectơ IA - 3 vectơ IB - vectơ IC = vectơ 0...

Một thùng đựng 39,75 kg đường, người ta lấy ra 10,5 kg rồi lại lấy tiếp 5 kg...

Một cửa hàng ngày thứ nhất bán được 35,5 mét vải, ngày thứ hai bán gấp đôi...

Hoàn thiện chương trình dưới đây, chương trình nhập từ bàn phím 3 số thực a, b, c...

Một của hàng bán vật liệu xây dựng có 127,5 tạ xi măng. Buổi sáng cửa hàng bán...

Đổi 123 phút = .......... giờ ...........phút...

ab + a + b = 95. Tìm ab...

Cho ∆ABC có AB = 2, AC = 3. Gọi M là trung điểm của đoạn thẳng BC...

Cho ∆ABC có AB = 6 cm, AC = 3 cm...

Cho tam giác ABC vuông tại A, kẻ đường cao AH. Gọi I, J là trung điểm của AH và HC...

Lớp 5A có số học sinh giỏi bằng 1/3 số học sinh cả lớp. Số học sinh khá bằng...

Trên 1 giá sách có 60 quyển sách. Biết 1/6 số sách giáo khoa bằng...

Cho f(x) = (m^2 - 3m + 2)x^2 + 2(2 - m)x - 2. Tìm m để f(x) = 0 có 2 nghiệm dương...

Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn...

Chứng minh bất đẳng thức: (a + b + c)(1/a + 1/b + 1/c) lớn hơn hoặc bằng 9...

Giải phương trình x^2 - 2nx - 5 = 0. Biết số nguyên dương n thỏa mãn...

Hiệu của 2 số bằng 0,14. Tìm 2 số đó, biết rằng 5 lần số lớn trừ đi số bé thì được 18,1...

Một vòi nước chảy vào cái bể không có nước trong 2h. Giờ đầu vòi chảy được 1/4 bể...

Tìm nghiệm âm lớn nhất của phương trình sinx + cosx = 1 - 1/2 sin2x...

Trong hệ tọa độ Oxy, cho 2 điểm A(2; 3); B(4; –1). Giao điểm của đường thẳng AB...

Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m...

Chứng minh rằng: Khoảng cách từ 1 điểm trên đường chéo của hình thoi đến các cạnh...

Lúc 8h, 1 ô tô đi từ Hà Nội với vận tốc 52 km/h, cùng lúc đó 1 xe thứ 2 đi từ...

Tìm GTNN của D = x^4 - 2x^3 + 3x^2 - 2x + 1...

Cho tam giác ABC có góc B = 60 độ, góc C = 40 độ, BC = 6cm...

Tìm tập xác định của hàm số y = (1 - 2cosx) / (sin3x - sinx)...

Tìm x biết: 150 - x^5 + 18 = 118...

Hai anh em cùng trồng 400 cây trên mảnh vườn của gia đình, nhiệm vụ mỗi anh em...

Làm tròn đến số thập phân thứ nhất: 0,2288...

Tìm số abc. Biết abc chia hết cho 45 và abc - cba = 396...

Cộng, trừ phân thức: 1 / (2x + 2) - (x - 1) / (3x^2 + 6x + 3)...

Tìm x biết: 2x(3x + 5) – x(6x – 1) = 33...

1 330 02/02/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: