Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 564 02/02/2024

Trang trước

Trang sau

Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD

Đề bài: Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, O là trung điểm của CD, $A D = 4 a, S A = S B = S O = 2 a .$ Tính khoảng cách giữa SA và CD.

Lời giải:

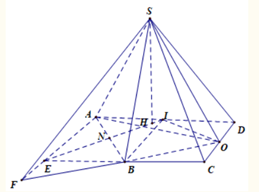
Tài liệu VietJack

Gọi I, N là trung điểm của AD, AB. Gọi H là tâm đường tròn ngoại tiếp tam giác ABO, vì tam giác ABI đều nên H thuộc NI.

Kẻ HK vuông góc CD, dựng hình bình hành AECD. Gọi F là giao điểm của BO và AE.

Ta có: $A F // C D,$ nên $d (S A, C D) = d (C D, (S A F)) = d (O, (S A F)) .$

Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, nên tam giác BIC và CID là các tam giác đều, do đó ta có:

$\begin{array}{l} A C = \sqrt{{(4 a)}^{2} - {(2 a)}^{2}} = 2 a \sqrt{3} \\ C O = \frac{1}{2} C D = a \\ A O = \sqrt{A C^{2} + C O^{2}} = \sqrt{12 a^{2} + a^{2}} = a \sqrt{13} \\ B O = \sqrt{B C^{2} + C O^{2} - 2 B C . C O . {cos120}^{0}} = \sqrt{4 a^{2} + a^{2} + 2 a^{2}} = a \sqrt{7} \\ S_{Δ A B O} = \frac{(2 a + 4 a) . a \sqrt{3}}{2} - \frac{1}{2} .2 a . \frac{a \sqrt{3}}{2} - \frac{1}{2} .4 a . \frac{a \sqrt{3}}{2} = \frac{3 a^{2} \sqrt{3}}{2} . \end{array}$

Suy ra

$\begin{array}{l} A H = \frac{2 a . a \sqrt{7} . a \sqrt{13}}{4. \frac{3 a \sqrt{3}}{2}} = \frac{a \sqrt{273}}{9} . \\ S H = \sqrt{S A^{2} - A H^{2}} = \sqrt{4 a^{2} - \frac{273 a^{2}}{81}} = \frac{a \sqrt{51}}{9} . \end{array}$

Diện tích $S_{Δ A F O} = 2 S_{Δ A B O} = 3 a^{2} \sqrt{3} .$

Thể tích của khối chóp S. AFO là: $V_{S . A F O} = \frac{1}{3} S H . S_{A F O} = \frac{a^{3} \sqrt{153}}{9} .$

Diện tích tam giác SAF:

$S A = 2 a, A F = 3 a \Rightarrow S B^{2} = \frac{S O^{2} + S F^{2}}{2} - \frac{F O^{2}}{4} \Rightarrow S F = 3 a \sqrt{2} \Rightarrow S_{Δ S A F} = \frac{a^{2} \sqrt{119}}{4} .$

Vậy $d (S A, C D) = d (C D, (S A F)) = d (O, (S A F)) = \frac{3 V_{O . S A F}}{S_{Δ S A F}} = \frac{3 \frac{a^{3} \sqrt{153}}{9}}{\frac{a^{2} \sqrt{119}}{4}} = \frac{2 a}{\sqrt{7}} .$

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác...

Ngày mùng 3 tháng 3 năm 2015 anh A vay ngân hàng 50 triệu đồng với lãi suất kép là...

Cho hình lập phương ABCD.A'B'C'D' có độ dài bằng 1. Gọi M, N, P, Q lần lượt là trung điểm...

Cho các hình sau thì có bao nhiêu hình là đa diện lồi...

Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B...

Cho hình lăng trụ đều ABC.A'B'C'. Biết rằng góc giữa (A'BC) và (ABC) là...

Hình lập phương có bao nhiêu mặt đối xứng...

Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số...

$y = |x^{3} - 3 x^{2} + m|,$ với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên...

Đồ thị hàm số $y = |x^{3}| - 3 x^{2} + 1$ có bao nhiêu điểm cực trị...

Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a...

Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a...

Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD...

Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân...

Cho G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai...

Cho hình nón có thiết diện qua trục là tam giác đều...

Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số...

Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số...

Từ các chữ số trong tập hợp X = {0; 1; 2; 3; 4; 5; 6} có thể lập được bao nhiêu số...

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = AA' = 2a...

Cho khối lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình bình hành có góc BAC...

Số cách chia 12 phần quà giống nhau cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà...

Có bao nhiêu cách xếp 3 học sinh nam và 2 học sinh nữ thành một hàng sao cho...

Từ một nhóm có 10 học sinh nam và 8 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh...

Từ các chữ số 0, 1, 2, 3, 4, 5, có thể lập bao nhiêu số gồm 3 chữ số khác nhau...

Từ các số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số...

Tính cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều...

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y = x^{3} - 8 x^{2} + (m^{2} + 11) x - 2 m^{2} + 2$ ...

Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng 2a...

Cho tam giác ABC, biết AB = 8, AC = 9, BC = 11. Gọi M là trung điểm của BC...

Cho P = căn x / căn x + 2...

Cho P = căn x / căn x - 1 ...

Tổng của hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng ...

Có ba chiếc hộp A, B, C mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1, 2, 3 ...

Chọn ngẫu nhiên ba số đôi một khác nhau từ tập hợp {1; 2; 3; ...; 100 ...

Cho x thuộc ℕ. Hãy chứng minh x^2 + 1 không chia hết cho 4 ...

Tồn tại n thuộc ℕ, n^2 + 11n + 2 chia hết cho 11 ...

Cho tam giác ABC vuông tại A có đường cao AH ...

Cho 4 điểm O, A, B, C sao cho vectơ OA + 2 vectơ OB - 3 vectơ OC = vectơ 0 ...

Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người ...

7x^2y − 14xy^2 + 21x ...

Tính: (14xy^2 + 21x^2y − 7x^3) : 7x ...

Đọc tên góc, đỉnh, và các cạnh của góc trong các hình vẽ sau ...

Đọc tên góc, đỉnh và các cạnh của góc trong Hình 85 và Hình 86 ...

Phân tích thành nhân tử: x^3 + y^3 + z^3 − 3xyz ...

Biết M(1; −6) là điểm cực đại của đồ thị hàm số ...

Tìm 3 số hạng liên tiếp của một cấp số cộng, biết tổng của chúng là 27 ...

Tìm cấp số cộng có 3 số hạng liên tiếp, biết tổng số của chúng là 15 ...

Nêu tính chất đối xứng của hình vuông, hình chữ nhật, hình thoi, hình bình hành ...

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông ...

1 564 02/02/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: