Tìm n để (n^2 – 8)^2 + 36 là số nguyên tố

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 1,733 15/11/2024

Trang trước

Trang sau

Tìm n để (n² – 8)² + 36 là số nguyên tố

Đề bài: Tìm n để (n² – 8)² + 36 là số nguyên tố.

Lời giải:

Ta có: (n² – 8)² + 36

= n⁴ – 16n² + 64 + 36

= n⁴ – 16n² + 100

= n⁴ + 20n² + 100 – 36n²

= (n² + 10)² – (6n)²

= (n² + 6n + 10)(n² – 6n + 10)

Để (n² – 8)² + 36 là số nguyên tố thì n² + 6n + 10 = 1 hoặc n² – 6n + 10 = 1

TH1: n² + 6n + 10 = 1

⇔ n² + 6n + 9 = 0

⇔ (n + 3)² = 0

⇔ n + 3 = 0

⇔ n = –3 (loại)

TH2: n² – 6n + 10 = 1

⇔ n² – 6n + 9 = 0

⇔ (n – 3)² = 0

⇔ n – 3 = 0

⇔ n = 3 (thỏa mãn)

Vậy n = 3 thì (n² – 8)² + 36 là số nguyên tố.

*Phương pháp giải:

Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức.

*Lý thuyết:

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

- Hợp số là số tự nhiên lơn hơn 1, có nhiều hơn hai ước.

Phân tích một số ra thừa số nguyên tố

Mọi số đều có thể phân tích ra tích của các thừa số nguyên tố

Cách phân tích một số ra thừa số nguyên tố:

+) Phương pháp phân tích bằng sơ đồ cây

Ví dụ 2. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cây:

Lời giải

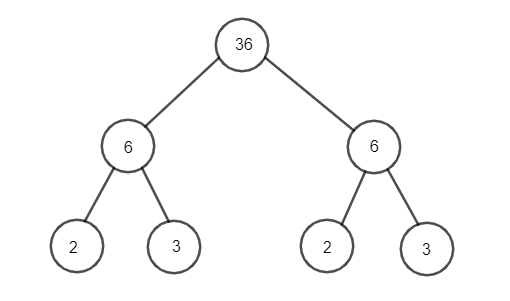
Lý thuyết Số nguyên tố chi tiết – Toán lớp 6 Kết nối tri thức (ảnh 1)

Vậy $36 = 2^{2} {.3}^{2}$ .

+) Phương pháp phân tích bằng sơ đồ cột

Ví dụ 3. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cột:

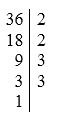
Lý thuyết Số nguyên tố chi tiết – Toán lớp 6 Kết nối tri thức (ảnh 1)

Vậy $36 = 2^{2} {.3}^{2}$ .

Xem thêm

Lý thuyết Số nguyên tố chi tiết – Toán lớp 6 Kết nối tri thức

TOP 40 câu Trắc nghiệm Số nguyên tố. Hợp số (Cánh diều 2024) có đáp án - Toán 6

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Tìm hai số tự nhiên, biết: a) Có tích bằng 720 và ƯCLN bằng 6...

Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh BC. Gọi D, E theo thứ tự ...

Tìm x, y ∈ ℕ, biết: (2x + 1)(y – 3) = 10 ...

Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số thập phân ...

Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số ...

Một tấm vải dài 36 m. Lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài ...

Chứng minh 43^43 – 17^17 chia hết cho 10 ...

Đổi đơn vị: 8 dam = … mm ...

Ở một nhà trẻ có một số cháu được chia thành các nhóm. Mỗi nhóm có một cô giáo ...

Một kho chứa 1000 bao gạo, trong đó có 350 bao gạo nếp, còn lại là các bao gạo tẻ ...

Một kho chứa 1000 bao gạo, trong đó có 450 bao gạo nếp, còn lại là các bao gạo tẻ ...

Tìm một số thập phân có chữ số ở phần thập phân là 3. Biết rằng nếu viết thêm chữ số ...

Tính nhanh: (–25) . (75 – 45) – 75 . (45 – 25 ...

Với mỗi số nguyên dương n, kí hiệu Sn là tổng của n số nguyên tố đầu tiên ...

Thắng có 25 viên bi xanh và 15 viên bi đỏ. Hỏi tỉ số phần trăm của số bi đỏ ...

Tính hợp lí: 19 . 25 + 9 . 95 + 19 . 30 ...

Một thế kỉ rưỡi bằng bao nhiêu năm ...

Tìm nghiệm nguyên dương của phương trình: x^3 – (x + y + z)^2 = (y + z)^3 + 34 ...

Tìm n để (n^2 – 8)^2 + 36 là số nguyên tố ...

Số chẵn bé nhất có 3 chữ số là bao nhiêu ...

Giải phương trình (x – 5)^4 + (x – 3)^4 = 16 ...

Tìm số tự nhiên lớn nhất thỏa mãn điều kiện: Số đó cộng với tổng các chữ số ...

Cho 1 số tự nhiên gồm các số tự nhiên liên tiếp nhau từ 1 đến 2021 ...

Có bao nhiêu phân số thập phân lớn hơn 1 và nhỏ hơn 5 có mẫu số là số có ...

Một buổi sáng cửa hàng bán được 45,8kg gạo, buổi chiều cửa hàng bán được ít hơn ...

Khi chia hai số tự nhiên a và b cho 3 thì cùng có số dư là r. Chứng minh rằng ...

Cho a, b là hai số nguyên tố cùng nhau. Chứng tỏ rằng 5a + 2b và 7a + 3b ...

Điền số thích hợp vào chỗ trống theo quy luật 24, 48, 80, 120 ...

Số a chia cho 5 dư 2, số b chia cho 5 dư 3. Hỏi a + b chia 5 dư mấy ...

Đổi 2 giờ 45 phút = ... giờ (là số thập phân ...

Một số nếu giảm đi 6 lần rồi thêm 25,71 thì được 88,5. Tìm số đó ...

Ba công nhân có năng suất lao động tương ứng tỉ lệ với 3, 5, 7 ...

Một người đi ô tô trong 2 giờ đầu, mỗi giờ đi được 42,5 km; trong 4 giờ sau ...

Trong một tháng có hai ngày đầu tháng và cuối tháng đều là chủ nhật ...

Tính chu vi và diện tích hình tròn có bán kính 4 cm ...

Hỏi có bao nhiêu phân số thập phân khác 0 mà tổng của mẫu số và tử số là số lẻ ...

Số nguyên tố là gì? Ví dụ minh họa ...

Có một cái ao ở giữa một khu đất, diện tích cái ao là 30,6 m2 và nhỏ hơn diện tích ...

Có tất cả bao nhiêu cặp số tự nhiên có trung bình cộng là 50 ...

Hai căn phòng hình chữ nhật. Căn phòng thứ nhất có chiều dài là 5,2 m ...

Hiệu của 2 số là 33, lấy số lớn chia cho số nhỏ được thương là 3 và số dư là 3 ...

Lãi suất tiết kiệm là 0,65% / tháng. Để sau một tháng nhận được tiền lãi là 832 000 ...

Một người bỏ ra 450 000 đồng tiền vốn để mua một cây quạt ...

Một người mua hai hộp kẹo, mỗi hộp chứa 4 túi kẹo, mỗi túi có 125 g kẹo ...

Một đoàn tàu gồm 15 toa, mỗi toa dài 14 m chạy với vận tốc 43,2 km/giờ ...

Một cửa hàng đã bán được 240 kg gạo và số gạo đó bằng 12,5% tổng số gạo ...

Tìm các ước của 10 ...

Nêu dấu hiệu chia hết cho cả 3 và 5 ...

a) Viết số tự nhiên nhỏ nhất có 3 chữ số ...

Theo kế hoạch, đội sản xuất phải trồng 15 ha rừng trong một năm ...

1 1,733 15/11/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: