Tìm a để hàm số khi x ≠ 1 có đạo hàm tại x = 1

Vietjack.me giới thiệu bộ câu hỏi ôn tập Toán có đáp án được biên soạn bám sát chương trình học giúp bạn ôn luyện và bổ sung kiến thức môn Toán tốt hơn. Mời các bạn đón xem:

1 2,598 16/11/2024

Trang trước

Trang sau

Tìm a để hàm số khi x ≠ 1 có đạo hàm tại x = 1

Đề bài: Tìm a để hàm số $f (x) = \{\begin{matrix} \frac{x^{2} - 1}{x - 1} \\ a k h i x = 1 \end{matrix}$ khi x ≠ 1 có đạo hàm tại x = 1.

Lời giải:

Để hàm số có đạo hàm tại x = 1 thì trước hết hàm số phải liên tục tại x = 1, tức là

$\lim_{x \to 1} f (x) = f (1) \Leftrightarrow \lim_{x \to 1} \frac{x^{2} - 1}{x - 1} = a \Leftrightarrow \lim_{x \to 1} (x + 1) = a \Leftrightarrow 2 = a$

Khi đó hàm số có dạng: $f (x) = \{\begin{matrix} \frac{x^{2} - 1}{x - 1} k h ix \neq 1 \\ 2 k h i x = 1 \end{matrix}$

$\Rightarrow f^{'} (1) = \lim_{x \to 1} \frac{f (x) - f (1)}{x - 1} = \lim_{x \to 1} \frac{\frac{x^{2} - 1}{x - 1} - 2}{x - 1} = \lim_{x \to 1} \frac{x + 1 - 2}{x - 1} = 1$

Vậy a = 2.

*Phương pháp giải:

+) Để hàm số có đạo hàm tại $x = 1$ thì hàm số phải liên tục tại $x = 1.$

+) Đạo hàm của hàm số $y = f (x)$ tại điểm $x = x_{0}$ là $f^{'} (x_{0}) = lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}}$ (nếu tồn tại).

*Lý thuyết:

Định nghĩa 1

Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

Hàm số y = f(x) được gọi là liên tục tại x₀ nếu $\lim_{x \to x_{0}} f (x) = f (x_{0}) .$

Ví dụ 1. Xét tính liên tục của hàm số $f (x) = \frac{2 x}{x - 1}$ tại x₀ = 2.

Giải

Hàm số đã cho xác định trên $ℝ \ \{1\}$ .

Do đó hàm số xác định trên khoảng $(1; + \infty)$ chứa x₀ = 2. Khi đó ta có:

$\lim_{x \to 2} f (x) = \lim_{x \to 2} \frac{2 x}{x - 1} = \frac{4}{1} = 4 = f (2)$ .

Vậy hàm số y = f(x) liên tục tại x₀ = 2.

II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

Định nghĩa 2

Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và $\lim_{x \to a^{+}} f (x) = f (a), \lim_{x \to b^{-}} f (x) = f (b) .$

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

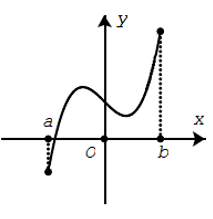
Lý thuyết Hàm số liên tục - Toán lớp 11 (ảnh 1)

Hàm số liên tục trên khoảng (a;b)

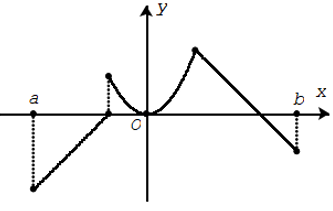
Lý thuyết Hàm số liên tục - Toán lớp 11 (ảnh 1)

Hàm số không liên tục trên khoảng (a; b).

III. MỘT SỐ ĐỊNH LÍ CƠ BẢN

Định lí 1

a) Hàm số đa thức liên tục trên toàn bộ tập số thực .

b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

b) Hàm số $\frac{f (x)}{g (x)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Xem thêm

Hàm số liên tục | Lý thuyết, công thức, các dạng bài tập và cách giải

TOP 40 câu Trắc nghiệm Hàm số liên tục (có đáp án ) – Toán 11

Xem thêm các câu hỏi ôn tập Toán chọn lọ, hay khác:

Hai góc tương ứng là gì...

Cho tam giác ABC, lấy D là trung điểm của AC. Từ A vẽ đường thẳng song song với BC...

Có bao nhiêu phân số thập phân có tử số là 3, lớn hơn...

Tìm x: $9 {(x + 1)}^{2} - (3 x - 2) (3 x + 2) = 10$ ...

Tú và Hiếu có 40 viên bi, sau khi Hiếu cho Tú 2 viên thì số bi của Hiếu bằng...

Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc...

Xác định 4 góc của một tứ giác lồi, biết rằng đo 4 góc lập thành 1 cấp số cộng...

Hiện nay bố 32 tuổi, con 5 tuổi . Hỏi mấy năm nữa thì tuổi bố gấp 4 lần tuổi con...

Tìm số thực a biết: $x^{4} - 6 x^{3} + 12 x^{2} - 14 x + 3 a$ chia x-2 dư 3...

Trong mặt phẳng Oxy cho đường thẳng 2x - y + 1 = 0. Để phép tịnh tiến theo vecto...

36dm =.......m...

Một tổ công nhân có 12 người. Cần chọn 3 người, một người làm tổ trưởng...

Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối...

Cho tam giác ABC có trọng tâm G. Khi đó...

Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm...

Tổng tất các nghiệm thuộc đoạn $[0,10 π]$ của phương trình...

Tính tổng T các nghiệm của phương trình sin2x – cosx = 0...

Thực hiện các phép tính...

Từ một điểm A nằm bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC...

Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD...

Một hộp chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ hộp đó...

Một hình chữ nhật có các kích thước 6 m và 2 m. Một hình tam giác có các cạnh...

Viết phương trình của đường thẳng y = ax + b thỏa mãn một trong các điều kiện sau...

Tìm nghiệm nguyên của phương trình x^2 + 5y^2 + 6z^2 + 2xy – 4xz = 10...

Cho hàm số y = (2m – 1)x + 2 (1) có đồ thị là đường thẳng dm...

Tìm x thuộc ℤ, biết: 11 chia hết cho (2x + 1...

Tìm x thuộc ℕ để 11.2x chia hết cho 2x – 1...

Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1...

Cho đường tròn (O; R). Vẽ 2 dây AB và CD vuông góc với nhau. Chứng minh...

Cho phương trình x^2 – 2mx + 2(m – 2) = 0. Tìm m để phương trình có 2 nghiệm...

Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC ...

Cho y = (1 – 2m)x + m + 1. Tìm m để y là hàm hằng ...

Tìm a để hàm số khi x ≠ 1 có đạo hàm tại x = 1 ...

Biết rằng hàm số liên tục trên khoảng [0; 1) (với a là tham số ...

Tìm các giá trị của m để x1; x2 thỏa mãn 2x1 – 3x2 = 5 ...

Cho 5 điểm A, B, C, D, E. Chứng minh rằng các vectơ AC + CD - EC = AE - DB + CB ...

Cho đường tròn (O) đường kính AB. Trên tia tiếp tuyến của (O) tại A ...

Cho đường tròn (O) đường kính AB. Trên tia tiếp tuyến của (O) tại A ...

Cho AC là đường kính của (O; R). Trên tiếp tuyến tại A của (O; R ...

Cho đường tròn (O, R) và 1 điểm A sao cho OA = 2R ...

Cho các số thực dương x, y, z, thỏa mãn x + 2y + 3z = 18 ...

Hiện nay anh 13 tuổi và em 3 tuổi. Hỏi sau bao nhiêu năm nữa thì tuổi anh ...

Rút gọn biểu thức A = 1/x-y + 1/x+y + 2x/x^2 + y^2 ...

Tìm điều kiện xác định của biểu thức P = (x = 2căn x) / căn x ...

Từ các chữ số 2, 3, 4 lập được bao nhiêu số tư nhiên có 9 chữ số ...

Chu vi 1 hình tứ giác là 23,4 m. Tổng độ dài cạnh 1, cạnh 2 và cạnh 3 là 18,9 m ...

Tính nhanh 19 – 42. (–19) + 38.5 ...

Một tổ 12 người làm trong 3 ngày được 144 sản phẩm ...

Một hình chữ nhật có chiều rộng bằng 36 cm ...

Một xí nghiệp gà giống trong 1 lần ra lò đã thu 10800 gà con giống ...

Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, ta lập được các số tự nhiên có 6 chữ số ...

Tìm x, biết: 2(x – 5) – 3(x + 7) = 14 ...

Cho ∆ABC. Gọi M, N lần lượt là trung điểm AB, AC. Chứng minh rằng ...

Làm tròn số 3,14159... đến chữ số thập phân thứ 3 ...

Giải phương trình: (tanx + 1) = 3sinx(cosx – sinx) + 3 ...

1 2,598 16/11/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: