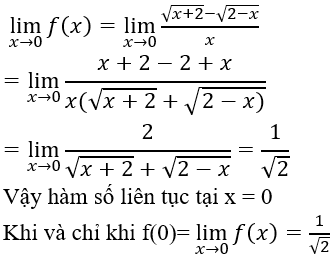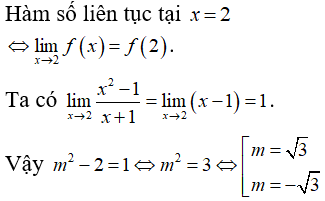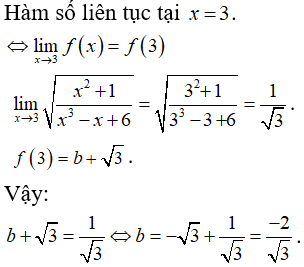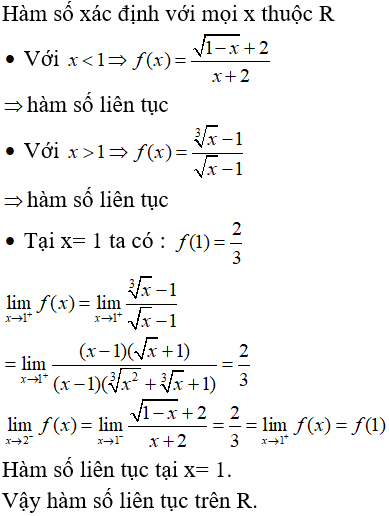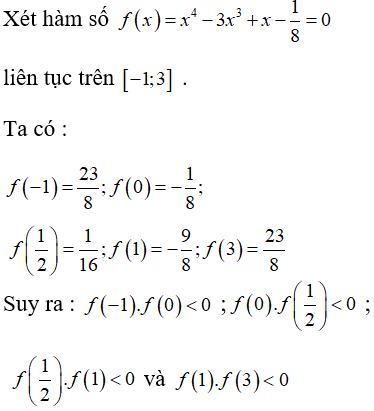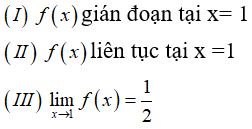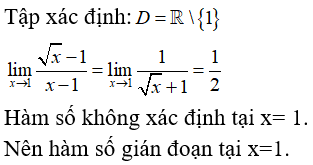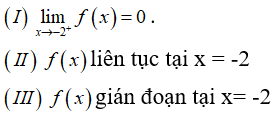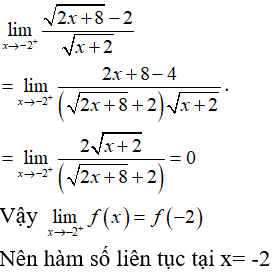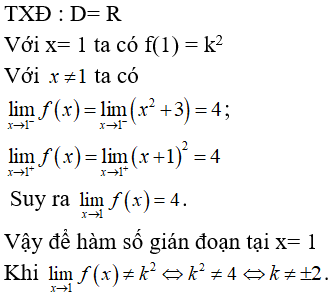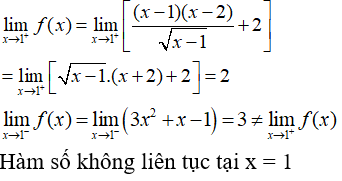TOP 40 câu Trắc nghiệm Hàm số liên tục (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 3: Hàm số liên tục có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 3.
Trắc nghiệm Toán 11 Bài 3: Hàm số liên tục
Bài giảng Trắc nghiệm Toán 11 Bài 3: Hàm số liên tục
Câu 1: Tính tổng (S ) gồm tất cả các giá trị m để hàm số f(x)={x2+x,x<12,x=1m2x+1,x>1 liên tục tại x=1.
A. S=−1
B. S=0
C. S=1
D. S=2
Đáp án: B
Giải thích:
Hàm số xác định với mọi x∈R.
Điều kiện bài toán trở thành
limx→1+f(x)=limx→1−f(x)=f(1).(*)
Ta có:
{f(1)=2limx→1+f(x)=limx→1+(m2x+1)=m2+1limx→1−f(x)=limx→1−(x2+x)=2⇒(*)⇔m2+1=2
⇔m=±1⇒S=0
Câu 2: Số điểm gián đoạn của hàm số h(x)={2x,x<0x2+1,0≤x≤23x−1,x>2 là:
A. 1
B. 2
C. 3
D. 0
Đáp án: A
Giải thích:
Hàm số y=h(x) có TXĐ: D=R
Dễ thấy hàm số y=h(x) liên tục trên mỗi khoảng (−∞;0),(0;2) và (2;+∞).
Ta có:
{h(0)=02+1=1limx→0−h(x)=limx→0−2x=0
⇒f(x) không liên tục tại x=0
Ta có:
{h(2)=5limx→2−h(x)=limx→2−(x2+1)=5limx→2+h(x)=limx→2+(3x−1)=5
⇒f(x) liên tục tại x=2
Câu 3: Cho hàm số f(x)={3−x√x+1−2,x≠3m,x=3 . Hàm số đã cho liên tục tại x=3 khi bằng :
A. −4
B. 4
C. −1
D. 1
Đáp án: A
Giải thích:
Ta có:
limx→3f(x)=limx→33−x√x+1−2=limx→3(3−x)(√x+1+2)x+1−4=limx→3(−√x+1−2)=−√3+1−2=−4
Để hàm số liên tục tại x=3 thì
limx→3f(x)=f(3)⇔m=−4
Câu 4: Cho hàm số f(x)={sin5x5x,x≠0a+2,x=0 . Tìm a để hàm số liên tục tại x = 0.
A. 1
B. −1
C. −2
D. 2
Đáp án: B
Giải thích:
Ta có:
limx→0sin5x5x=1;f(0)=a+2
Vậy để hàm số liên tục tại x=0 thì a+2=1⇔a=−1
Câu 5: Tìm giá trị thực của tham số m để hàm số f(x)={x3−x2+2x−2x−1,x≠13x+m,x=1 liên tục tại x=1
A. m=0
B. m=2
C. m=4
D. m=6
Đáp án: A
Giải thích:
Hàm số xác định với mọi x∈R.
Ta có: f(1) = 3.1 + m = 3+ m
limx→1f(x)=limx→1x3−x2+2x−2x−1=limx→1x2(x−1)+2(x−1)x−1=limx→1(x−1)(x2+2)x−1=limx→1(x2+2)=3
Để hàm số liên tục tại x = 1 thì phải có: limx→1f(x)=f(1)
Nên m + 3 = 3 ⇔m=0
Câu 6: Cho hàm số f(x) xác định trên [a;b]. Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu hàm số f(x) liên tục trên đoạn [a;b] và f(a).f(b)>0 thì phương trình f(x)=0 không có nghiệm trong khoảng (a;b)
B. Nếu f(a).f(b)<0 thì phương trình f(x)=0 có ít nhất một nghiệm trong khoảng (a;b)
C. Nếu phương trình f(x)=0 có nghiệm trong khoảng (a;b) thì hàm số y=f(x) liên tục trên khoảng (a;b)
D. Nếu hàm số y=f(x) liên tục tăng trên đoạn [a;b] và f(a).f(b)>0 thì phương trình f(x)=0 không thể có nghiệm trong (a;b)
Đáp án: D
Giải thích:
Đáp án A sai. Chẳng hạn xét hàm số f(x)=x2−5. Hàm số này xác định trên [−3;3] và liên tục trên đoạn đó, đồng thời f(−3).f(3)=16>0 nhưng phương trình f(x)=x2−5=0 có nghiệm x=±√5∈(−3;3)
Đáp án B sai vì thiếu điều kiện f(x) liên tục trên (a;b)
Đáp án C sai. Ví dụ xét hàm số f(x)={x+1,x<0x+2,x≥0. Hàm số này xác định trên [−3;3], có nghiệm thuộc khoảng (−3;3) nhưng gián đoạn tại điểm x=0∈(−3;3) nên không liên tục trên khoảng (−3;3).
Đáp án D đúng. Thật vậy:
+ Vì hàm số y=f(x) liên tục tăng trên đoạn [a;b] nên f(a)<f(x)<f(b)∀x∈(a;b)
TH1:
{f(a>0f(b)>0f(a)<f(x)<f(b)
⇒f(x)>0
TH2:
{f(a)<0f(b)<0f(x)<f(b)
⇒f(x)<0
Vậy không có giá trị nào của x để f(x)=0 hay phương trình f(x)=0 không thể có nghiệm trong (a;b)
Câu 7: Tìm khẳng định đúng trong các khẳng định sau:
( I ) f(x) liên tục trên đoạn [ (a;b) ] và f(a).f(b)>0 thì tồn tại ít nhất một số c∈(a;b) sao cho
(II) )Nếu f(x) liên tục trên đoạn (a;b] và trên [b;c) thì không liên tục (a;c)
A. Chỉ (I).
B. Chỉ (II).
C. Cả (I) và (II)đúng
D. Cả (I) và (II)sai.
Đáp án: D
Giải thích:
KĐ 1 sai vì f(a).f(b)>0 vẫn có thể xảy ra trường hợp f(x)=0 vô nghiệm trên khoảng
KĐ 2 sai vì nếu f(x) liên tục trên đoạn (a;b] và trên [b;c) thì liên tục (a;c)
Câu 8: Hàm số f(x)={−xcosx,x<0x21+x,0≤x<1x3,x≥1
A. Liên tục tại mọi điểm trừ điểm x=0.
B. Liên tục tại mọi điểm trừ x=1.
C. Liên tục tại mọi điểm trừ hai điểm x=0 và x=1.
D. Liên tục tại mọi điểm x∈R.
Đáp án: B
Giải thích:
Hàm số y=f(x) liên tục trên các khoảng (−∞;0), (0;1), (1;+∞) nên ta chỉ xét tính liên tục của y=f(x) tại các điểm x=0; x=1.
limx→0+f(x)=limx→0+x21+x=021+0=0limx→0−f(x)=limx→0+(−xcosx)=−0.cos0=0f(0)=01+0=0}⇒limx→0+f(x)=limx→0−f(x)=f(0)
⇒Hàm số liên tục tại x=0
limx→1+f(x)=limx→1+x3=13=1limx→1−f(x)=limx→1−x21+x=121+1=12}⇒limx→1+f(x)≠limx→1−f(x)
Không tồn tại limx→1f(x)
Hàm số không liên tục tại x=1.
Vậy hàm số liên tục tại mọi điểm trừ x=1 .
Câu 9: Cho hàm số f(x)={x−83√x−2,x>8ax+4,x≤8. Để hàm số liên tục tại x=8, giá trị của a là:
A. 1
B. 2
C. 4
D. 3
Đáp án: A
Giải thích:
limx→8+f(x)=limx→8+x−83√x−2=limx→8+(3√x2+23√x+4)=3√82+2.3√8+4=12limx→8−f(x)=limx→8−(ax+4)=8a+4f(8)=8a+4
Hàm số liên tục tại x=8
⇔12=8a+4⇔a=1
Câu 10: Cho hàm số f(x)=x3−1000x2+0,01. Phương trình f(x)=0. có nghiệm thuộc khoảng nào trong các khoảng:
I. (−1;0)
II. (0;1)
III. (1;2)
IV. (2;1000)
A. Chỉ I, II, III.
B. Chỉ I và II
C. Chỉ I, II, IV.
D. Cả I, II, III IV.
Đáp án: C
Giải thích:
TXĐ: D=R
Hàm số f(x)=x3−1000x2+0,01 liên tục trên nên liên tục trên [−1;0], [0;1], [1;2] và [2;1000] (1).
Ta có f(−1)=−1000,99; f(0)=0,01
suy ra f(−1).f(0)<0. (2)
Từ (1)và (2) suy ra phương trình f(x)=0 có ít nhất một nghiệm trên khoảng (−1;0)
Ta có f(0)=0,01;f(1)=−999,99
suy ra f(0).f(1)<0.(3)
Từ (1) và (3) suy ra phương trình có ít nhất một nghiệm trên khoảng (0;1).
Ta có f(1)=−999,99,f(2)=−39991,99
suy ra f(1).f(2)>0.(4)
Từ (1) và (4) ta chưa thể kết luận về nghiệm của phương trình f(x)=0 trên khoảng (1;2).
Ta có: f(2)=−39991,99<0,f(1000)=0,01>0 nên phương trình f(x)=0 có ít nhất 1 nghiệm thuộc khoảng (2;1000)
Mà phương trình bậc ba chỉ có nhiều nhất ba nghiệm nên ở mỗi khoảng I, II, IV thì phương trình đều có 1 nghiệm và trên khoảng (1;2) không có nghiệm.
Câu 11: Cho hàm f(x)={x2−1x−1,x≠14,x=1√x+3,x≥3 . Hàm số f(x) liên tục tại:
A. mọi điểm thuộc R.
B. mọi điểm trừ x=1 .
C. mọi điểm trừ x=3.
D. mọi điểm trừ x=1 và x=3.
Đáp án: D
Giải thích:
Hàm số y=f(x) có TXĐ: D = R .
Dễ thấy hàm số y=f(x) liên tục trên mỗi khoảng (−∞;1), (1;3) và (3;+∞).
Ta có :
{f(1)=4limx→1f(x)=limx→1x2−1x−1=limx→1(x+1)=2
⇒ f(x) gián đoạn tại x=1
Ta có :
{f(3)=2limx→3−f(x)=limx→3−x2−1x−1=limx→3−(x+1)=4
⇒f(x) gián đoạn tại x=3
Câu 12: Cho hàm số f(x)={3−√9−xx,0<x<9m,x=03x,x≥9 . Tìm m để f(x) liên tục trên [0;+∞)
A. 13
B. 12
C. 16
D. 1
Đáp án: C
Giải thích:
Hàm số liên tục trên (0;9) ∪ (9;+∞), ta cần xét tính liên tục của hàm số tại x=0 và x=9
limx→0+f(x)=limx→0+3−√9−xx=limx→0+9−(9−x)x(3+√9−x)=limx→0+13+√9−x=13+ √9−0=16
Mà f(0)=m⇒ để hàm số liên tục tại x=0 thì limx→0+f(x)=f(0)⇔16=m
limx→9+f(x)=limx→9+3x= 39=13limx→9−f(x)=limx→9−3−√9−xx=3−√9−99=13f(9)=39=13}
⇒limx→9+f(x)=limx→9−f(x)=f(9)
⇒ hàm số liên tục tại x=9.
Vậy với m=16 thì hàm số liên tục trên [0;+∞)
Câu 13: Biết rằng f(x)={x2−1√x−1,x≠1a,x=1 liên tục trên đoạn (0;1) (với a là tham số). Khẳng định nào dưới đây về giá trị a là đúng?
A. a là một số nguyên
B. a là một số vô tỉ
C. a > 5.
D. a < 0.
Đáp án: A
Giải thích:
Hàm số xác định và liên tục trên [0;1). Khi đó liên tục trên [0;1] khi và chỉ khi
limx→1−f(x)=f(1).(*)
Ta có :
{f(1)=alimx→1−f(x)=limx→1−x2−1√x−1=limx→1−[(x+1)(√x+1).√x−1]√x−1=limx→1−[(x+1)(√x+1)]=4⇒(*)⇔a=4
Câu 14: Cho hàm số (f( x )) liên tục trên đoạn [−1;4] sao cho f(−1)=2; f(4)=7. Có thể nói gì về số nghiệm của phương trình f(x)=5 trên đoạn [−1;4]:
A. Vô nghiệm.
B. Có ít nhất một nghiệm.
C. Có đúng một nghiệm.
D. Có đúng hai nghiệm.
Đáp án: B
Giải thích:
Ta có f(x)=5⇔f(x)−5=0
Đặt g(x)=f(x)−5
Khi đó
{g(−1)=f(−1)−5=2−5=−3g(4)=f(4)−5=7−5=2
⇒g(−1).g(4)<0
Vậy phương trình g(x)=0 có ít nhất một nghiệm thuộc khoảng (1;4) hay phương trình f(x)=5 có ít nhất một nghiệm thuộc khoảng (1;4).
Câu 15: Cho hàm số f(x)=x3−3x−1. Số nghiệm của phương trình f(x)=0 trên R là:
A. 0.
B. 1.
C. 2.
D. 3.
Đáp án: D
Giải thích:
Hàm số f(x)=x3−3x−1 là hàm đa thức có tập xác định là R nên liên tục trên R. Do đó hàm số liên tục trên mỗi khoảng (−2;−1),(−1;0),(0;2).
Ta có:
•{f(−2)=−3f(−1)=1⇒f(−2).f(−1)<0
⇒(1) có ít nhất một nghiệm thuộc (-2;-1)
•{f(−1)=1f(0)=−1⇒f(−1).f(0)<0
⇒(1) có ít nhất một nghiệm thuộc (-1;0)
•{f(2)=1f(0)=−1⇒f(2).f(0)<0
⇒(1) có ít nhất một nghiệm thuộc (0;2)
Như vậy phương trình (1) có ít nhất ba nghiệm thuộc khoảng (−2;2)
Tuy nhiên phương trình f(x)=0 là phương trình bậc ba có nhiều nhất ba nghiệm.
Vậy phương trình f(x)=0 có đúng 3 nghiệm trên.
Câu 16: Cho hàm số f(x)={tanxx,x≠0;x≠π2+k2π(k∈R)0,x=0. Hàm số y=f(x) liên tục trên các khoảng nào sau đây?
A. (0;π2)
B. (−∞;π4)
C. (−π4;π4)
D. R
Đáp án: A
Giải thích:
limx→0f(x)=limx→0tanxx=limx→0sinxx.1cosx=limx→0sinxx.limx→01cosx=1.1cos0=1f(0)=0}
⇒limx→0f(x)≠f(0)=0
⇒ hàm số gián đoạn tại điểm x=0 , do đó loại các đáp án B, C, D.
Câu 17: Biết rằng limx→0sinxx=1. Tìm giá trị thực của tham số để hàm số
f(x)={1+cosx(x−π)2,x≠πm,x=π liên tục tại x=π
A. m=π2
B. m=−π2
C. m=12
D. m=−12
Đáp án: C
Giải thích:
Hàm số xác định với mọi x∈R. Điều kiện của bài toán trở thành:
m=f(π)=limx→πf(x)=limx→π1+cosx(x−π)2=limx→π2cos2x2(x−π)2=limx→π2sin2(x2−π2)(x−π)2=limx→π142sin2(x2−π2)14(x−π)2=limx→π12sin2(x2−π2)(x−π2)2=12limx→πsin2(x−π2)(x−π2)2=12limx→π[sin(x−π2)(x−π2)]2(*)
Đặt t=x2−π2→0 khi x→1.
Khi đó (∗) trở thành:
m=12limt→0(sintt)2=12.12=12
Câu 18: Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để hàm số f(x)={√ax+1−1x,x≠04x2+5b,x=0 liên tục tại x = 0.
A. a=5b
B. a=10b
C. a=b
D. a=2b
Đáp án: B
Giải thích:
limx→0f(x)=limx→0√ax+1−1x=limx→0ax+1−1x(√ax+1+1)=limx→0a√ax+1+1
=a√a.0+1+1=a2
f(0)=5b
Để hàm số liên tục tại x=0 thì
limx→0f(x)=f(0)⇔a2=5b⇔a=10b
Câu 19: Cho hàm số y=f(x) có đồ thị như hình vẽ, chọn kết luận đúng:
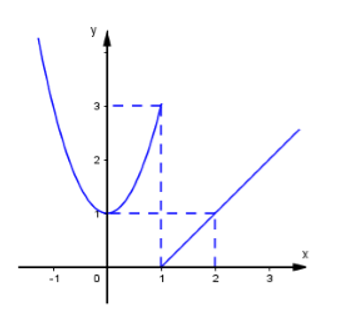
A. Hàm số liên tục trên khoảng (0;3).
B. Hàm số liên tục trên khoảng (0;2).
C. Hàm số không liên tục trên khoảng (−∞;0).
D. Hàm số không liên tục trên khoảng (0;4).
Đáp án: D
Giải thích:
Quan sát đồ thị ta thấy
limx→1−f(x)=3;limx→1+f(x)=0⇒limx→1−f(x)≠limx→1+f(x) nên không tồn tại limx→1f(x).
Do đó hàm số gián đoạn tại điểm x=1.
Do đó hàm số không liên tục trên mọi khoảng có chứa điểm x=1 hay A, B sai, D đúng.
Đáp án C sai do hàm số liên tục trên khoảng (−∞;0).
Câu 20: Cho hàm số f(x)=x2+1x2+5x+6. Hàm số f(x) liên tục trên khoảng nào sau đây?
A. (−∞;3)
B. (2;3)
C. (−3;2)
D. (−3;+∞)
Đáp án: B
Giải thích:
TXĐ:
D=R\{−3;−2}=(−∞;−3)∪(−3;−2)∪(−2;+∞)
nên theo định lí 1, hàm số liên tục trên các khoảng (−∞;−3)∪(−3;−2)∪(−2;+∞).
Vì (2;3)⊂(−2;+∞)
⇒ Hàm số liên tục trên (2;3).
Câu 21: Hàm số f(x)=√3−x+1√x+4 liên tục trên:
A. [−4;3].
B. [−4;3).
C. (−4;3].
D. [−∞;−4]∪[3;+∞).
Đáp án: C
Giải thích:
Điều kiện:
{x+4>03−x≤0⇔{x>−4x≤3
⇔−4<x≤3
TXĐ: D=(-4;3].
Với mọi x0∈(−4; 3) ta có:
limx→x0f(x)=limx→x0(√3−x+1x+4)
=√2−x0+1x0+4=f(x0)
Do đó, hàm số liên tục trên (−4;3).
Xét tại x=3, ta có:
limx→3−f(x)=limx→3−(√3−x+1x+4)=√3−3+13+4=17⇒limx→3−f(x)=f(3)
Do đó hàm số liên tục trái tại x=3
Vậy hàm số liên tục trên (−4;3].
Câu 22: Hàm số f(x)={x4+xx2+x,khix≠0,x≠−13,khix=−11,khix=0
A. Liên tục tại mọi điểm trừ điểm thuộc đoạn (−1;0)
B. Liên tục tại mọi điểm trừ x = 0.
C. Liên tục tại mọi điểm
D. Liên tục tại mọi điểm trừ x=−1
Đáp án: C
Giải thích:
Hàm phân thức y=x4+xx2+x có txđ D=R∖{0;−1} và liên tục trên các khoảng (−∞;−1),
(- 1; 0) và (0;+∞).
Ta chỉ cần xét tính liên tục của y=f(x) tại các điểm x=0; x=−1
Ta có:
limx→−1f(x)=limx→−1x4+xx2+x=limx→−1x3+1x+1=limx→−1(x2−x+1)=3=f(−1)
⇒ Hàm số liên tục tại x=−1
limx→0f(x)=limx→0x4+xx2+x=limx→0x3+1x+1=1=f(0)
⇒ Hàm số liên tục tại x=0
Vậy hàm số liên tục tại mọi điểm x∈R.
Câu 23: Tìm giá trị nhỏ nhất của a để hàm số f(x)={x2−5x+6√4x−3−x,x>31−a2x,x≤3 liên tục tại x=3.
A. −2√3
B. 2√3
C. −43
D. 43
Đáp án: A
Giải thích:
Ta có:
f(x)={x2−5x+6√4x−3−x,x>31−a2x,x≤3
f(3)=1−3a2limx→3+f(x)=limx→3+f(x)x2−5x+6√4x−3−x=limx→3+(x−2)(x−3)(√4x−3+x)(√4x−3−x)(√4x−3+x)=limx→3+(x−2)(x−3)(√4x−3+x)4x−3−x2=limx→3+(x−2)(x−3)(√4x−3+x)−(x−3)(x−1)=limx→3+(x−2)(√4x−3+x)−(x−1)=(3−2)(√12−3+3)−(3−1)=−3limx→3−f(x)=limx→3−(1−a2x)=1−3a2
Do đó hàm số liên tục tại
x=3⇔limx→3+f(x)=limx→3−f(x)=f(3)⇔1−3a2=−3⇔−3a2=−4⇔a2=43⇔a=±2√3⇒amin=−2√3
Câu 24: Tìm tất cả các giá trị của tham số m sao cho phương trình x3−3x2+(2m−2)x+m−3=0 có ba nghiệm x1,x2,x3 thỏa mãn x1<−1<x2<x3
A. m>−5
B. m<−5
C. m≤−3
D. m<−6
Đáp án: B
Giải thích:
Đặt f(x)=x3−3x2+(2m−2)x+m−3.
Ta thấy hàm số liên tục trên R.
Dễ thấy nếu x→−∞ thì f(x)→−∞ hay f(x)<0
nếu x→+∞ thì f(x)→+∞ hay f(x)>0
Suy ra điều kiện cần để f(x)=0 có 3 nghiệm thỏa x1<−1<x2<x3 là:
f(−1)>0⇔−1−3.1+(2m−2).(−1)+m−3>0⇔−m−5>0⇔m<−5
Điều kiện đủ: với m<−5 ta có
*) limx→−∞f(x)=−∞ nên tồn tại a<−1 sao cho f(a)<0
Mặt khác f(−1)=−m−5>0.
Suy ra f(a).f(−1)<0
Do đó tồn tại x1∈(a;−1) sao cho f(x1)=0
*) f(0)=m−3<0,f(−1)>0. Suy ra f(0).f(−1)<0
Do đó tồn tại x2∈(−1;0) sao cho f(x2)=0
*) limx→+∞f(x)=+∞ nên tồn tại b>0 sao cho f(b)>0
Mặt khác f(0)<0. Suy ra f(0).f(b)<0
Do đó tồn tại x3∈(0;b) sao cho f(x3)=0
Vậy m<−5 thỏa mãn yêu cầu bài toán.
Câu 25: Tìm giá trị lớn nhất của a để hàm số. f(x)={3√3x+2−2x−2,x>2a2x−74,x≤2 liên tục tại x=2
A. amax=3
B. amax=0
C. amax=1
D. amax=2
Đáp án: C
Giải thích:
Để hàm số liên tục tại x = 2 thì:
limx→2+f(x)=limx→2−f(x)=f(2).(*)
Ta có : f(2)=2a2−74
limx→2−f(x)=limx→2−(a2x−74)=2a2−74limx→2+f(x)=limx→2+3√3x+2−2x−2=limx→2+(3√3x+2−2)(3√(3x+2)2+23√3x+2+4)(x−2)(3√(3x+2)2+23√3x+2+4)=limx→2+3x−6(x−2)(3√(3x+2)2+23√3x+2+4)=limx→2+3(3√(3x+2)2+23√3x+2+4)=14(*)⇔2a2−74=14⇔8a2−7=1⇔a2=1 ⇔a=±1⇒amax=1
Câu 26: Biết rằng limx→0=sinxx=1. Tìm giá trị thực của tham số m để hàm số f(x)={sinπxx−1,x≠1m,x=1 liên tục tại x=1.
A. m=−π
B. m=π
C. m=−1
D. m=1
Đáp án: A
Giải thích:
Tập xác định D=R . Điều kiện bài toán tương đương với
m=f(1)=limx→1f(x)=limx→1sinπxx−1=limx→1−sin(πx−π)x−1=limx→1−sinπ(x−1)x−1=limx→1[(−π).sinπ(x−1)π(x−1)](*)
Đặt t=π(x−1) thì t→0 khi x→1. Do đó (*) trở thành:
m=limt→0(−π).sintt=−π
Câu 27: Cho hàm số f(x)={cosπx2,|x|≤1|x−1|,|x|>1. Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại x=1 và x= −1
B. Hàm số liên tục tại x=1, không liên tục tại điểm x= −1.
C. Hàm số không liên tục tại x=1 và x=−1.
D. Tất cả đều sai.
Đáp án: B
Giải thích:
Ta có:
f(x)={cosπx2,|x|≤1|x−1|,|x|>1⇔f(x)={cosπx2,−1≤x≤1|x−1|,[x>1x<−1
Ta có:
limx→1+f(x)=limx→1+|x−1|=0limx→1−f(x)=limx→1−cosπx2=cosπ2=0f(1)=cosπ2=0}⇒limx→1+f(x)=limx→1−f(x)=f(1)=0
Hàm số liên tục tại x=1
limx→(−1)+f(x)=limx→∞cosπx2=cos−π2=0limx→(−1)−f(x)=limx→(−1)−|x−1|=2}⇒limx→(−1)+f(x)≠limx→(−1)−f(x)
⇒ Hàm số không liên tục tại x=−1.
Câu 28: Cho phương trình 2x4−5x2+x+1=0(1). Trong các mệnh đề sau, mệnh đề nào đúng?
A. Phương trình (1) chỉ có một nghiệm trong (-2;1)
B. Phương trình (1) có ít nhất hai nhiệm trong khoảng (2;0)
C. Phương trình (1) không có nghiệm trong khoảng (-2;0)
D. Phương trình (1) không có nghiệm trong khoảng (-1;1)
Đáp án: B
Giải thích:
TXĐ: D=R.
Hàm số f(x)=2x4−5x2+x+1 liên tục trên .
Ta có:
f(−1)=−3,f(0)=1⇒f(−1)f(0)<0
Phương trình (1) có ít nhất một nghiệm trong (-1;0) (-2;1)
Ta có:
f(0)=1;f(1)=−1⇒f(0).f(1)<0
Phương trình (1) có ít nhất 1 nghiệm thuộc (0;1) (-2;1)
Phương trình (1) có ít nhất hai nghiệm trong (-2;1)
Đáp án A sai.
Ta có:
f(−1)=−3,f(0)=1⇒f(−1)f(0)<0
Phương trình (1) có ít nhất một nghiệm trong (-1;0) (-2;0)
Đáp án C sai.
Ta có:
f(0)=1;f(1)=−1⇒f(0).f(1)<0
Phương trình (1) có ít nhất một nghiệm trong (0;1) (-1;1)
Đáp án D sai.
Câu 29: Giá trị thực của tham số để hàm số f(x)={x2sin1x,x≠0m , x=0 liên tục tại x=0 thỏa mãn điều kiện nào dưới đây?
A. m∈(−2;−1)
B. m≤−2
C. m∈[−1;7)
D. m∈[7;+∞)
Đáp án: C
Giải thích:
Với mọi x≠0 ta có;
0≤|f(x)|=|x2sin1x|≤x2→0 khi
x→0⇒limx→0f(x)=limx→0x2.sin 1x =0
Mà f(0) = m nên để hàm số liên tục tại x = 0 thì :
m=f(0)=limx→0f(x)=0
Câu 30: Chọn giá trị của f(0) đề hàm số f(x)={3√2x+8−2√3x+4−2,x≠0m,x=0 liên tục tại điểm x=0.
A. 1
B. 2
C. 29
D. 19
Đáp án: C
Giải thích:
limx→0f(x)=limx→03√2x+8−2√3x+4−2=limx→0(2x+8−8)(√3x+4+2)(3√2x+82+23√2x+8+4)(3x+4−4)=limx→02(√3x+4+2)3(3√2x+82+23√2x+8+4)=2.(2+2)3.(22+2.2+4)=29
Hàm số liên tục tại điểm x=0 khi và chỉ khi
limx→0f(x)=f(0)⇔f(0)=29
Câu 31: Cho hàm số 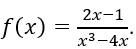
A. Hàm số f(x) liên tục tại điểm x = -2
B. Hàm số f(x) liên tục tại điểm x = 0
C. Hàm số f(x) liên tục tại điểm x = 0,5
D. Hàm số f(x) liên tục tại điểm x = 2
Đáp án: C
Giải thích:
Hàm số đã cho không xác định tại x = 0, x = -2, x = 2 nên không liên tục tại các điểm đó. Hàm số liên tục tại x = 0,5 vì nó thuộc tập xác định của hàm phân thức f(x).
Câu 32: Cho 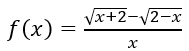
Đáp án: C
Giải thích:
Câu 33: Cho hàm số 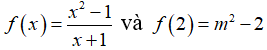
Đáp án: C
Giải thích:
Câu 34: Cho hàm số 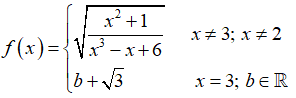
Đáp án: D
Giải thích:
Câu 35: Cho hàm số 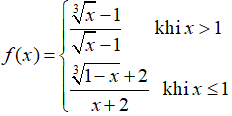
A. Hàm số liên tục trên R
B. Hàm số không liên tục trên R
C. Hàm số không liên tục trên (1; +∞)
D. Hàm số gián đoạn tại các điểm x= 1.
Đáp án: A
Giải thích:
Câu 36: Cho phương trình 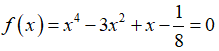
A. Phương trình (1) có đúng một nghiệm trên khoảng (-1; 3).
B. Phương trình (1) có đúng hai nghiệm trên khoảng (-1; 3).
C. Phương trình (1) có đúng ba nghiệm trên khoảng (-1; 3).
D. Phương trình (1) có đúng bốn nghiệm trên khoảng (-1; 3).
Đáp án: D
Giải thích:
Do đó phương trình có ít nhất 4 ngiệm thuộc khoảng (-1; 3).
Mặt khác phương trình bậc 4 có tối đa bốn nghiệm.
Vậy phương trình có đúng 4 nghiệm thuộc khoảng (-1; 3).
Câu 37: Cho hàm số 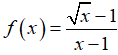
A. Chỉ (I).
B. Chỉ (III)
C. Chỉ (I) và (III)
D. Chỉ (II) và (III)
Đáp án: C
Giải thích:
Câu 38: Cho hàm số 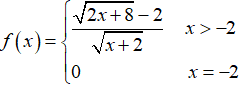
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II)
Đáp án: B
Giải thích:
Câu 39: Cho hàm số 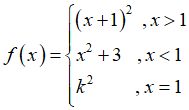
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
Đáp án: A
Giải thích:
Câu 40: Cho hàm số 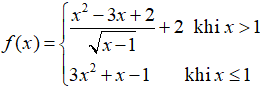
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x = 1
D. Tất cả đều sai
Đáp án: C
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Bài ôn tập chương 4 có đáp án
Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm có đáp án
Trắc nghiệm Quy tắc tính đạo hàm có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án