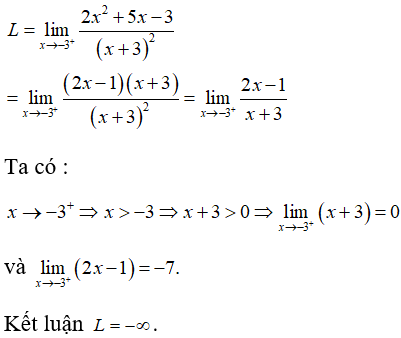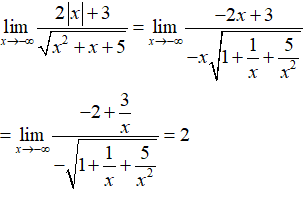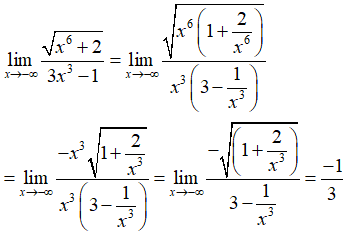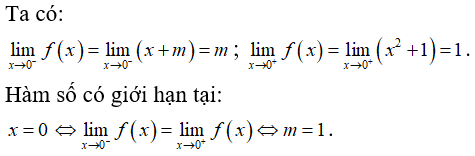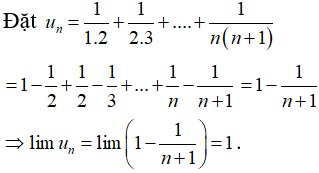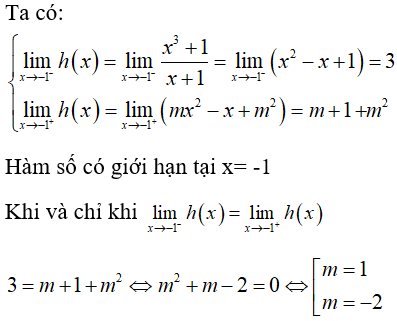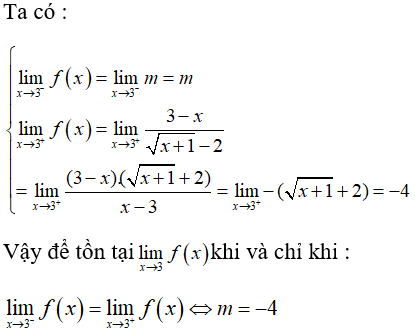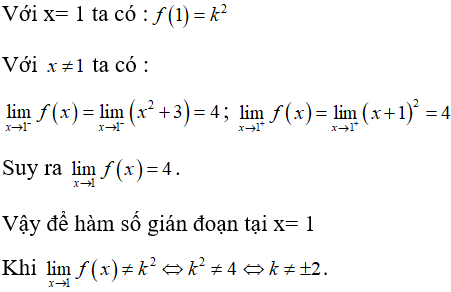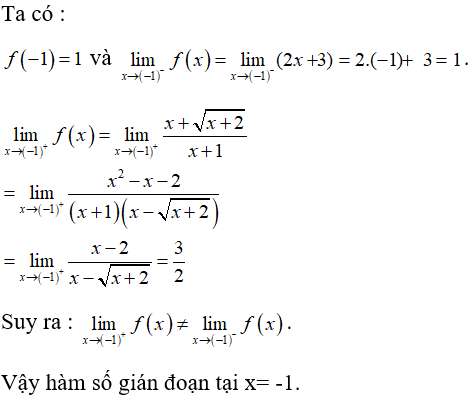TOP 40 câu Trắc nghiệm Bài ôn tập chương 4 (có đáp án 2023) – Toán 11

Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài ôn tập chương 4 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài Ôn tập chương 4.

1 1,414 12/01/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 11 Bài: Ôn tập chương 4

Câu 1: Biết $\lim u_{n} = 5; \lim v_{n} = a; \lim (u_{n} + 3 v_{n}) = 2018$ , khi đó a bằng

A. 617

B. $\frac{2018}{3}$

C. $\frac{2023}{3}$

D. 671

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$\lim (u_{n} + 3 v_{n}) = 2018$

$\Leftrightarrow 5 + 3 a = 2018 \Leftrightarrow a = 671$ .

Câu 2: Giá trị của giới hạn $\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$ là

A. $- \frac{3}{2}$

B. 0

C. – 2

D. 1

Hiển thị đáp án

Đáp án: B

Giải thích:

$\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$

$= \frac{1 - 1}{(2.1 - 1) (1 - 3)} = 0$

Câu 3: Kết quả của giới hạn $\lim_{x \to - \infty} \frac{2 x^{2} + 5 x - 3}{x^{2} + 6 x + 3}$ là

A. 2

B. 3

C. – 2

D. $+ \infty$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

$\begin{array}{l} \lim_{x \to - \infty} \frac{2 x^{2} + 5 x - 3}{x^{2} + 6 x + 3} \\ = \lim_{x \to - \infty} \frac{x^{2} (2 + \frac{5}{x} - \frac{3}{x^{2}})}{x^{2} (1 + \frac{6}{x} + \frac{3}{x^{2}})} \\ = \lim_{x \to - \infty} \frac{2 + \frac{5}{x} - \frac{3}{x^{2}}}{1 + \frac{6}{x} + \frac{3}{x^{2}}} = 2 \end{array}$

Câu 4: Cho giới hạn $\lim_{x \to - \infty} \frac{4 x^{3} - 1}{3 x^{2} + x + 2} = - \frac{a}{b}$ với $a, b \in ℤ$ và $\frac{a}{b}$ là phân số tối giản. Chọn kết quả đúng trong các kết quả sau:

A. $a = 11, b = 4$

B. $a = 11, b = 3$

C. $a = 10, b = 3$

D. $a = 11, b = 5$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\lim_{x \to - 2} \frac{4 x^{3} - 1}{3 x^{2} + x + 2} = - \frac{11}{4}$ .

Vậy $a = 11$ và $b = 4$

Câu 5: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. $\lim \frac{1}{n^{k}} = 0$ với k là số nguyên dương.

B. Nếu $|q| < 1$ thì $\lim q^{n} = 0$

C. Nếu $\lim u_{n} = a$ và $\lim v_{n} = b$ thì $\lim \frac{u_{n}}{v_{n}} = \frac{a}{b}$

D. Nếu $\lim u_{n} = a$ và $\lim v_{n} = + \infty$ thì $\lim \frac{u_{n}}{v_{n}} = 0$

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì phải có điều kiện $b \neq 0$

Câu 6: Tính giới hạn $\lim_{x \to {(- 2)}^{-}} \frac{3 + 2 x}{x + 2}$

A. 2

B. $- \infty$

C. $+ \infty$

D. $\frac{3}{2}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $\lim_{x \to {(- 2)}^{-}} (3 + 2 x) = - 1 < 0$ ;

$\lim_{x \to {(- 2)}^{-}} (x + 2) = 0$ và khi $x \to {(- 2)}^{-}$ thì $x + 2 < 0$ nên

$\lim_{x \to {(- 2)}^{-}} \frac{3 + 2 x}{x + 2} = + \infty$

Câu 7: Chọn khẳng định sai trong các khẳng định sau:

A. Hàm số $y = 5 x^{3} + x - 2$ liên tục trên $ℝ$

B. Hàm số $y = \frac{3 x - 5}{x + 3}$ liên tục trên $ℝ$

C. Hàm số $y = \frac{2 x^{2} - x}{x + 1}$ liên tục trên $(- \infty; - 1)$ và $(- 1; + \infty)$

D. Hàm số $y = x^{5} + 3 x^{2} + 5$ liên tục trên $ℝ$

Hiển thị đáp án

Đáp án: B

Giải thích:

Xét hàm số $y = \frac{3 x - 5}{x + 3}$ ta có

Tập xác định là $D = ℝ \ \{- 3\}$

Hàm số $y = \frac{3 x - 5}{x + 3}$ liên tục trên khoảng $(- \infty; - 3)$ và $(- 3; + \infty)$

Câu 8: Trong các giới hạn dãy số dưới đây, giới hạn có kết quả đúng là

A. $\lim (- 3 n^{4} + 3) = - \infty$

B. $\lim (- 3 n^{4} + 3) = 0$

C. $\lim (- n^{4} + 2) = + \infty$

D. $\lim (5 n^{4} - 2) = - \infty$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\lim (- 3 n^{4} + 3) = \lim n^{4} (- 3 + \frac{3}{n^{4}})$

Do $\lim n^{4} = \infty$ $\lim (- 3 + \frac{3}{n^{4}}) = - 3 < 0$ nên

$\lim (- 3 n^{4} + 3) = \lim n^{4} (- 3 + \frac{3}{n^{4}}) = - \infty$

Câu 9: $\lim_{x \to 3^{+}} \frac{4 x - 3}{x - 3}$ có kết quả là

A. 9

B. 0

C. $- \infty$

D. $+ \infty$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\lim_{x \to 3^{+}} \frac{4 x - 3}{x - 1} = + \infty$ do

$\{\begin{cases} \lim_{x \to 3^{+}} (4 x - 3) = 9 > 0 \\ \underset{x \to 3^{+}}{\lim (x - 3) = 0 (x - 3 > 0)} \end{cases}$

Câu 10: Hàm số nào dưới đây gián đoạn tại $x = - 2$ ?

A. $y = 2 x^{2} + x - 5$

B. $y = \frac{x + 5}{x - 2}$

C. $y = \frac{1}{x + 2}$

D. $y = \frac{x - 2}{2 x}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số $y = \frac{1}{x + 2}$ bị gián đoạn tại $x = - 2$ vì $y (- 2)$ không tồn tại.

Câu 11: Trong các hàm số sau, hàm số nào liên tục tại $x = 1$ ?

A. $y = \sqrt{x + 3}$

B. $y = \frac{x + 5}{x - 1}$

C. $y = \frac{3 x}{x^{2} + x - 2}$

D. $y = \sqrt{x - 4}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số $y = \frac{3 x}{x^{2} + x - 2}$ bị gián đoạn tại $x = 1$ vì $y (1)$ không tồn tại.

Câu 12: Tính $\lim_{x \to + \infty} (- 2 x^{3} - 4 x^{2} + 5)$ .

A. 2

B. 3

C. $- \infty$

D. $+ \infty$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

$\begin{array}{l} \lim_{x \to + \infty} (- 2 x^{3} - 4 x^{2} + 5) \\ = \lim_{x \to + \infty} [x^{3} (- 2 - \frac{4}{x} + \frac{5}{x^{3}})] = - \infty \end{array}$ do

$\{\begin{cases} \lim_{x \to + \infty} x^{3} = + \infty \\ \lim_{x \to + \infty} (- 2 - \frac{4}{x} + \frac{5}{x^{3}}) = - 2 < 0 \end{cases}$

Câu 13: Mệnh đề nào sau đây sai?

A. $\lim \frac{n + 3}{n^{2} + 1} = 0$

B. $\lim \frac{n + 1}{n - 1} = 1$

C. $\lim \frac{1}{2 n + 1} = \frac{1}{2}$

D. $\lim (2 n + 1) = + \infty$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $\lim \frac{1}{2 n + 1} = \lim \frac{\frac{1}{n}}{2 + \frac{1}{n}} = 0$

Câu 14: Giới hạn $\lim_{x \to a^{-}} \frac{1}{x - a}$ bằng

A. $+ \infty$

B. 0

C. $\frac{- 1}{2 a}$

D. $- \infty$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$\begin{array}{l} \{\begin{cases} \lim_{x \to a^{-}} 1 = 1 > 0 \\ \lim_{x \to a^{-}} (x - a) = 0 \\ x \to a^{-} \Rightarrow x - a < 0 \end{cases} \\ \Rightarrow \lim_{x \to a^{-}} \frac{1}{x - a} = - \infty \end{array}$

Câu 15: Trong các giới hạn sau đây, giới hạn nào là 0?

A. $\lim 3^{n}$

B. $\lim \frac{2 n^{2} - 3 n + 1}{n^{3} + 4 n^{2} - 3}$

C. $\lim n^{k} (k \in ℕ^{*})$

D. $\lim \frac{n^{3}}{n^{2} + 3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\begin{array}{l} \lim \frac{2 n^{2} - 3 n + 1}{n^{3} + 4 n^{2} - 3} \\ = \lim \frac{\frac{2}{n} - \frac{3}{n^{2}} + \frac{1}{n^{3}}}{1 + \frac{4}{n} - \frac{3}{n^{3}}} = 0 \end{array}$

Câu 16: Tính giới hạn $L = \lim_{x \to 1} \frac{|- 2 x|}{x + 1}$ .

A. $L = - 2$

B. $L = 1$

C. $L = - 1$

D. $L = 2$

Hiển thị đáp án

Đáp án: B

Giải thích:

$L = \lim_{x \to 1} \frac{|- 2 x|}{x + 1} = \frac{|- 2|}{2} = 1$

Câu 17: Giá trị của $\lim \frac{1}{n^{k}} (k \in ℕ^{*})$ bằng

A. 4

B. 0

C. 2

D. 5

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $\lim \frac{1}{n^{k}} = 0$

Câu 18: Cho hàm số $f (x)$ thỏa mãn $\lim_{x \to 2018^{+}} f (x) = - 2018$ và $\lim_{x \to 2018^{-}} f (x) = 2018$ . Khi đó khẳng định nào sau đây đúng:

A. $\lim_{x \to 2018} f (x) = 0$

B. $\lim_{x \to 2018} f (x) = 2018$

C. $\lim_{x \to 2018} f (x) = - 2018$

D. Không tồn tại $\lim_{x \to 2018} f (x) .$

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì $\begin{array}{l} \lim_{x \to 2018} f (x) = L \\ \Leftrightarrow \lim_{x \to 2018^{+}} f (x) = \lim_{x \to 2018^{-}} f (x) = L \end{array}$

Mà đầu bài

$\lim_{x \to 2018^{+}} f (x) = - 2018 \neq 2018 = \lim_{x \to 2018^{-}} f (x)$

Câu 19: Cho dãy số $(u_{n}), (v_{n})$ thỏa $\lim u_{n} = 2, \lim v_{n} = 1$ . Tính $\lim (2 u_{n} - 3 v_{n})$ .

A. 1

B. 2

C. 3

D. 7

Hiển thị đáp án

Đáp án: A

Giải thích:

$\begin{array}{l} \lim (2 u_{n} - 3 v_{n}) \\ = 2 \lim (u_{n}) - 3 \lim (v_{n}) \\ = 2.2 - 3.1 = 1 \end{array}$

Câu 20: Hàm số $y = f (x)$ có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?

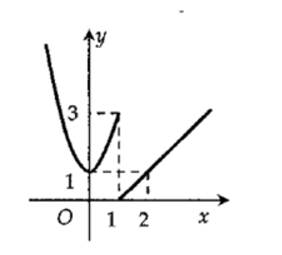
Trắc nghiệm Bài ôn tập chương 4 có đáp án – Toán lớp 11 (ảnh 3)

A. 0

B. 1

C. 3

D. 2

Hiển thị đáp án

Đáp án: B

Giải thích:

Đồ thị hàm số $y = f (x)$ gián đoạn tại điểm có hoành độ $x = 1$

Câu 21: Cho $\lim_{x \to 1} \frac{\sqrt{x + 1} - 2}{2 - x} = \sqrt{a} - b$ với $a, b \in ℕ, 0 \leq a, b \leq 3$ , khi đó $a + 2 b$ bằng

A. 3

B. 6

C. 4

D. 2

Hiển thị đáp án

Đáp án: B

Giải thích:

$\lim_{x \to 1} \frac{\sqrt{x + 1} - 2}{2 - x} = \sqrt{2} - 2$

suy ra $a = 2, b = 2$ nên $a + 2 b = 6$

Câu 22: Trong các giới hạn, giới hạn nào không tồn tại?

A. $\lim_{x \to 3} (x^{2} - 3 x + 2)$

B. $\lim_{x \to 3} \sqrt{16 - x^{2}}$

C. $\lim_{x \to 3} \frac{x^{2} - 9}{x + 3}$

D. $\lim_{x \to 3} \sqrt{x^{2} - 9}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có

$\begin{array}{l} x^{2} - 9 > 0 \\ \Leftrightarrow x \in (- \infty; - 3) \cup (3; + \infty) \end{array}$

$\lim_{x \to 3^{+}} \sqrt{x^{2} - 9} = 0$ và $\lim_{x \to 3^{-}} \sqrt{x^{2} - 9}$ không tồn tại nên không tồn tại $\lim_{x \to 3} \sqrt{x^{2} - 9}$

Câu 23: Cho a là một hằng số, $\lim_{x \to + \infty} \frac{a \sqrt{x^{2} - 2 x} + x - 3}{2 + \sqrt{x^{2} + 1}}$ có giá trị bằng

A. $\frac{a + 1}{2}$

B. a

C. $a + 1$

D. $1 - a$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

$\begin{array}{l} \lim_{x \to + \infty} \frac{a \sqrt{x^{2} - 2 x} + x - 3}{2 + \sqrt{x^{2} + 1}} \\ = \lim_{x \to + \infty} \frac{a \sqrt{1 - \frac{2}{x}} + 1 - \frac{3}{x}}{\frac{2}{x} + \sqrt{1 + \frac{1}{x^{2}}}} \\ = a + 1 \end{array}$

Câu 24: Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{x} - 2}{x - 4} k h i x > 4 \\ a x + \frac{5}{4} k h i x \leq 4 \end{cases}$ , trong đó a là một hằng số đã biết. Hàm số có giới hạn hữu hạn tại $x = 4$ khi và chỉ khi

A. $a = 1$

B. $a = - 1$

C. $a = - \frac{1}{4}$

D. $a = \frac{1}{4}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

$\begin{array}{l} \lim_{x \to 4^{+}} \frac{\sqrt{x} - 2}{x - 4} \\ = \lim_{x \to 4^{+}} \frac{x - 4}{(x - 4) (\sqrt{x} - 2)} \\ = \lim_{x \to 4^{+}} \frac{1}{(\sqrt{x} + 2)} = \frac{1}{4} \end{array}$

$\lim_{x \to 4^{+}} (a x + \frac{5}{4}) = 4 a + \frac{5}{4}$

Hàm số có giới hạn hữu hạn tại $x = 4$ khi và chỉ khi

$\begin{array}{l} \lim_{x \to 4^{+}} f (x) = \lim_{x \to 4^{-}} f (x) \\ \Leftrightarrow \frac{1}{4} = 4 a + \frac{5}{4} \Leftrightarrow a = - \frac{1}{4} \end{array}$

Câu 25: Tìm giá trị thực của tham số m để hàm số $f (x) = \{\begin{cases} \frac{x^{2} - x - 2}{x - 2} k h i x \neq 2 \\ m k h i x = 2 \end{cases}$ liên tục tại $x = 2$

A. $m = 0$

B. $m = 2$

C. $m = 1$

D. $m = 3$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to 2} \frac{x^{2} - x - 2}{x - 2} \\ = \lim_{x \to 2} (x + 1) = 3 \end{array}$

$f (2) = m$

Hàm số liên tục tại $x = 2 \Leftrightarrow m = 3$

Câu 26: Biết rằng $\lim_{x \to - \sqrt{3}} \frac{5 x^{3} + 15 \sqrt{3}}{3 - x^{2}} = a \sqrt{3} + b$ với $a, b \in ℚ$ . Tính $a^{2} + b^{2}$

A. $\frac{15}{2}$

B. $\frac{225}{4}$

C. $\frac{- 225}{4}$

D. $\frac{225}{2}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\begin{array}{l} \lim_{x \to - \sqrt{3}} \frac{5 x^{3} + 15 \sqrt{3}}{3 - x^{2}} \\ = \lim_{x \to - \sqrt{3}} \frac{5 (x + \sqrt{3}) (x^{2} - x \sqrt{3} + 3)}{(\sqrt{3} - x) (\sqrt{3} + x)} \\ = \lim_{x \to - \sqrt{3}} \frac{5 (x^{2} - x \sqrt{3} + 3)}{\sqrt{3} - x} \\ = \frac{15 \sqrt{3}}{2} \end{array}$

$\Rightarrow a = \frac{15}{2}, b = 0$

Vậy $a^{2} + b^{2} = \frac{225}{4}$ .

Câu 27: Cho hàm số $f (x) = \{\begin{cases} \frac{x^{3} - x^{2} + 2 x - 2}{x - 1} k h i x \neq 1 \\ 3 x + m k h i x = 1 \end{cases}$ . Để $f (x)$ liên tục tại $x = 1$ thì m bằng

A. 1

B. 0

C. 2

D. – 1

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\begin{array}{l} \lim_{x \to 1} f (x) \\ = \lim_{x \to 1} \frac{x^{3} - x^{2} + 2 x - 2}{x - 1} \\ = \lim_{x \to 1} (x^{2} + 2) = 3 \end{array}$

$f (1) = 3 + m$

Hàm số đã cho liên tục tại $x = 1$ khi và chỉ khi

$\lim_{x \to 1} f (x) = f (1)$ $\Leftrightarrow 3 + m = 3 \Leftrightarrow m = 0$

Câu 28: Cho hàm số $f (x) = \{\begin{cases} 3 x + a - 1 k h i x \leq 0 \\ \frac{\sqrt{1 + 2 x} - 1}{x} k h i x > 0 \end{cases}$ . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm $x = 0$ .

A. $a = 1$

B. $a = 3$

C. $a = 2$

D. $a = 4$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $f (0) = a - 1$ và $\lim_{x \to 0^{+}} f (x) = a - 1,$

$\lim_{x \to 0^{-}} f (x)$

$= \lim_{x \to 0^{-}} \frac{\sqrt{1 + 2 x} - 1}{x}$

$= \lim_{x \to 0^{-}} \frac{2}{\sqrt{1 + 2 x} + 1} = 1$

Hàm số đã cho liên tục tại điểm $x = 0$ khi $x = 0$

$\begin{array}{l} \lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{-}} f (x) \\ \Leftrightarrow a - 1 = 1 \Leftrightarrow a = 2 \end{array}$

Câu 29: Trong các giới hạn dưới đây, giới hạn nào bằng $+ \infty$ ?

A. $\lim_{x \to 4^{-}} \frac{2 x - 1}{4 - x}$

B. $\lim_{x \to + \infty} (- x^{3} + 2 x + 3)$

C. $\lim_{x \to - \infty} \frac{x^{2} + x + 1}{x - 1}$

D. $\lim_{x \to 4^{+}} \frac{2 x - 1}{4 - x}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$\lim_{x \to 4^{-}} \frac{2 x - 1}{4 - x} = + \infty$

$\lim_{x \to + \infty} [x^{3} (- 1 + \frac{2}{x^{2}} + \frac{3}{x^{3}})] = - \infty$

$\lim_{x \to - \infty} \frac{x^{2} + x + 1}{x - 1}$

$= \lim_{x \to - \infty} \frac{1 + \frac{1}{x} + \frac{1}{x^{2}}}{\frac{1}{x} - \frac{1}{x^{2}}} = - \infty$

$\lim_{x \to 4^{+}} \frac{2 x - 1}{4 - x} = - \infty$

Câu 30: Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 1}{x - 1} k h i x \neq 1 \\ m - 2 k h i x = 1 \end{cases}$ . Tìm m để hàm liên tục trên $ℝ$ .

A. $m = 4$

B. $m = - 4$

C. $m = 1$

D. $m = 2$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có hàm số $f (x) = \frac{x^{2} - 1}{x - 1} \forall x \neq 1$ nên hàm số $f (x)$ liên tục trên mỗi khoảng $(- \infty; 1)$ và $(1; + \infty)$

Ta có $\lim_{x \to 1} \frac{x^{2} - 1}{x - 1} = \lim_{x \to 1} (x + 1) = 2$ và $f (1) = m - 2$

Hàm số $f (x)$ liên tục trên $ℝ$ thì hàm số liên tục tại $x = 1$ hay

$\begin{array}{l} \lim_{x \to 1} \frac{x^{2} - 1}{x - 1} = f (1) \\ \Leftrightarrow 2 = m - 2 \Leftrightarrow m = 4 \end{array}$

Câu 31: Tính 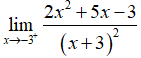Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 .

A. + ∞.

B. +-∞.

C. 0

D. – 7

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 32: Tính 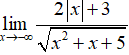Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 .

A. 0

B. - ∞.

C. 2

D. - 2

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 33: Tính 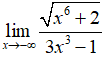Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 .

A. -1/3.

B. - ∞.

C. 1/3.

D. + ∞.

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 34: Tìm các giá trị thực của tham số m để hàm số 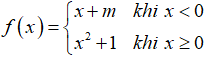Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 có giới hạn tại x= 0.

A. m = -1

B. m = 2

C. m = -2

D. m = 1

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 35: Cho dãy số (u_n) với 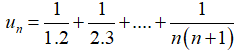Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 . Khi đó lim un bằng

A. 0.

B. 1.

C. 1/2.

D. 100

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 36: Biết hàm số 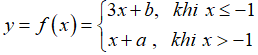Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 có giới hạn tại x = -1. Giá trị của a - b bằng

A. - 1

B. - 2

C. 2

D. 1

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 37: Tìm các giá trị thực của tham số m để hàm số để hàm số có 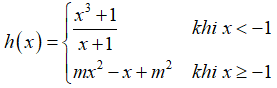Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 giới hạn tại x= -1.

A. m = -1; m = 2.

B. m = -1; m = -2.

C. m = 1; m = -2.

D. m = 1; m = 2.

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 38: Tìm các giá trị thực của tham số a để hàm số 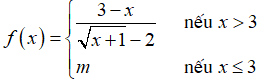Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 để tồn tại .

A. m = -1

B. m = 4

C. m = -4

D. m = 1

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 39: Cho hàm số 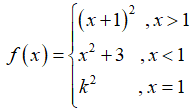Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 . Tìm k để f(x) gián đoạn tại x= 1.

A. k ≠ ± 2.

B. k ≠ 2.

C. k ≠ -2.

D. k ≠ ± 1.

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 40: Cho hàm số 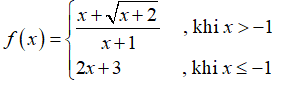Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 . Khẳng định nào sau đây đúng nhất:

A. Hàm số liên tục tại x = -1.

B. Hàm số liên tục tại mọi điểm.

C. Hàm số gián đoạn tại x = -1.

D. Tất cả đều sai.

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm có đáp án

Trắc nghiệm Quy tắc tính đạo hàm có đáp án

Trắc nghiệm Đạo hàm của hàm số lượng giác có đáp án

Trắc nghiệm Vi phân có đáp án

Trắc nghiệm Đạo hàm cấp hai có đáp án

1 1,414 12/01/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3