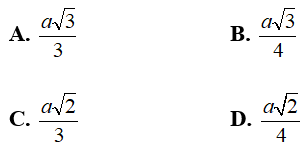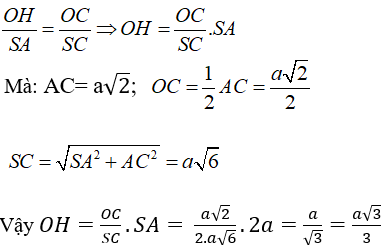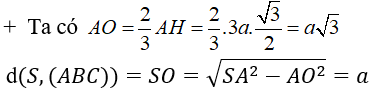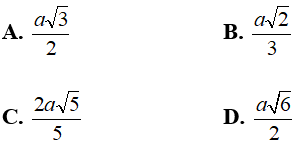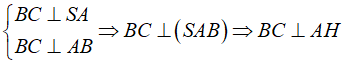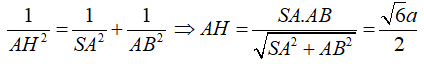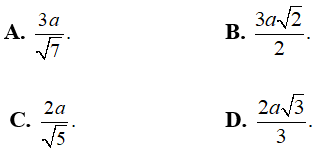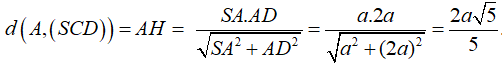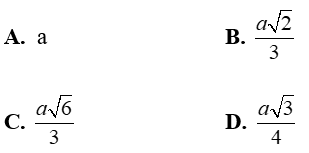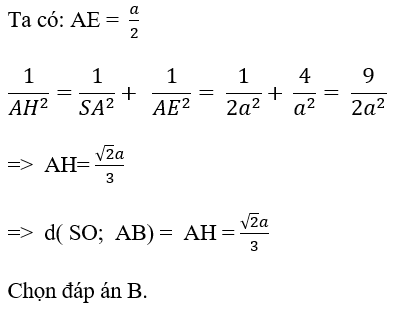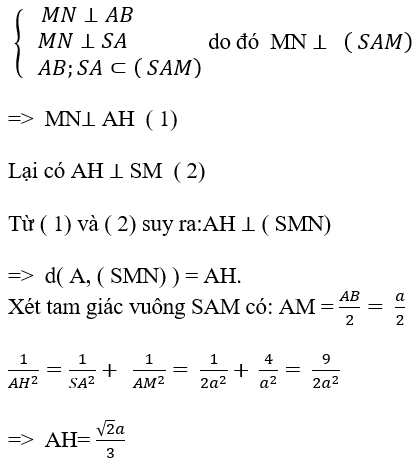TOP 40 câu Trắc nghiệm Khoảng cách (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 5: Khoảng cách có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 5.
Trắc nghiệm Toán 11 Bài 5: Khoảng cách
Câu 1: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2,BC=a. Khoảng cách từ S đến BC bằng bao nhiêu?
A. 2a
B. 4a
C. 3a
D. 5a
Đáp án: D
Giải thích:
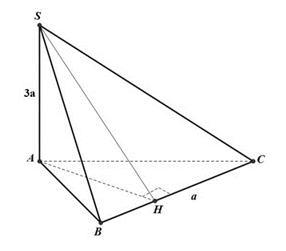
Kẻ AH vuông góc với BC
SΔABC=12AH.BC
→AH=2.SΔABCBC
=4a2a=4a
Khoảng cách từ S đến BC chính là SH
Dựa vào tam giác vuông ΔSAH ta có
SH=√SA2+AH2
=√(3a)2+(4a)2=5a
Câu 2: Cho hình chóp S.ABCD trong đó SA,AB,BC đôi một vuông góc và SA=AB=BC=1. Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau ?
A. √2.
B. √3.
C. 2.
D. √32.
Đáp án: B
Giải thích:
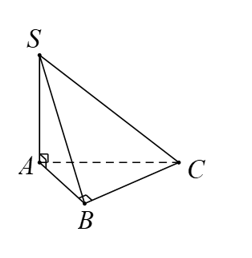
Do {SA⊥ABSA⊥BC nên SA⊥(ABC)
⇒SA⊥AC
Như vậy SC=√SA2+AC2
=√SA2+(AB2+BC2)=√3
Câu 3: Cho hình chóp A.BCD có cạnh AC⊥(BCD) và BCD là tam giác đều cạnh bằng a. Biết AC=a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
A. a√75.
B. a√47.
C. a√611.
D. a√23.
Đáp án: C
Giải thích:
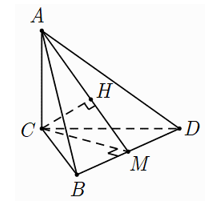
Do ΔABC đều cạnh a nên đường cao MC=a√32
d(C,AM)=CH
=AC.MC√AC2+MC2=a√6611
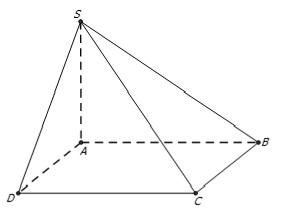
Câu 4: Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA= a . Khoảng cách từ A đến (SBC) bằng
A. a√5.
B. 2a.
C. a√217.
D. a√3.
Đáp án: C
Giải thích:
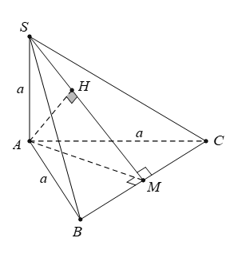
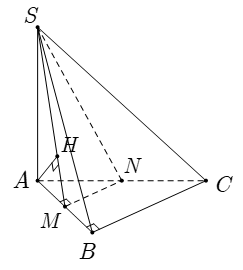
Gọi M là trung điểm của BC; H là hình chiếu vuông góc của A trên SM.
Ta có BC⊥AM và BC⊥SA nên
BC⊥(SAM)⇒BC⊥AH.
Mà AH⊥SM, do đó AH⊥(SBC).
Vậy AH=d(A,(SBC)).
AM=a√32;
AH=AS.AM√AS2+AM2=a√217.
Câu 5: Cho tứ diện SABC trong đo SA, SB, SC vuông góc với nhau từng đôi một và SA=3a, SB=a,SC=2a. Khoảng cách từ A đến đường thẳng BC bằng:
A. 3a√22
B. 7a√55
C. 8a√33
D. 5a√66
Đáp án: B
Giải thích:
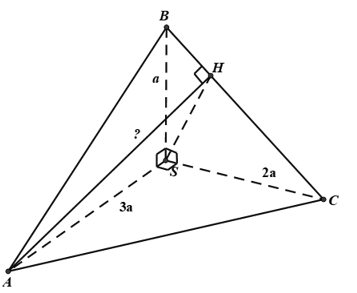
+ Dựng AH⊥BC ⇒d(A,BC)=AH
+ {AS⊥(SBC)⊃BC⇒AS⊥BCAH⊥BC
AH cắt Á cùng nằm trong (SAH).
⇒BC⊥(SAH)⊃SH⇒BC⊥SH
Xét trong ΔSBC vuông tại S có H là đường cao ta có:
1SH2=1SB2+1SC2
=1a2+14a2=54a2
⇒SH2=4a25
⇒SH=2a√55
+ Ta dễ chứng minh được AS⊥(SBC)⊃SH⇒AS⊥SH
⇒ΔASH vuông tại S.
Áp dụng hệ thức lượng trong ΔASH vuông tại S ta có:
AH2=SA2+SH2
=9a2+4a25=49a25
⇒AH=7a√55
Câu 6: Cho hình chóp S.ABCD có SA⊥( ABCD), mặt đáy ABCD là hình thang vuông có chiều cao AB=a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
A. a√22
B. a√33
C. a2
D. a3
Đáp án: C
Giải thích:
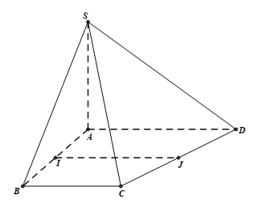
SA⊥(ABCD)⇒SA⊥AI
Lại có AI⊥AD ( hình thang vuông)
suy ra IA⊥(SAD)
IJ∥AD theo tính chất hình thang, nên
d(IJ,(SAD))=d(I,(SAD))
=IA=a2
Câu 7: Cho hình thang vuông ABCD vuông ở A và D, AD= 2a .Trên đường thẳng vuông góc với (ABCD) tại D lấy điểm S với SD=a√2. Tính khoảng cách giữa DC và (SAB).
A. 2a√3
B. a√2
C. a√2.
D. a√33
Đáp án: A
Giải thích:
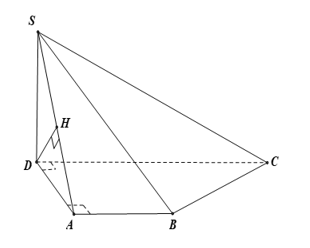
Trong tam giác DHA , dựng DH⊥SA;
Vì DC//AB
⇒d(DC;(SAB))=d(D;(SAB))
=DH
Xét tam giác vuông SDA có :
1DH2=1SD2+1AD2
⇒DH=a√123=2a√3
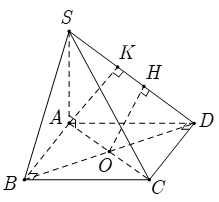
Câu 8: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Khi đó khoảng cách giữa đường thẳng AB và mặt phẳng (SCD) bằng
A. a√62
B. a√64
C. 2a√69
D. a√63
Đáp án: D
Giải thích:
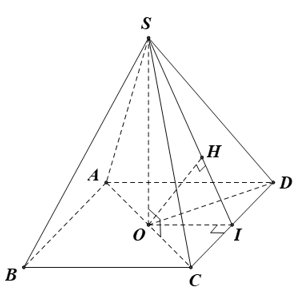
Gọi O là tâm hình vuông ABCD
Khi đó SO⊥(ABCD)
Kẻ OI⊥CD, OH⊥SI
⇒OH⊥(SCD)
Ta tính được AO=a√22,
SO=√SA2−AO2=a√22
1OH2=1SO2+1OI2
⇒OH=a√66
⇒d(A,(SCD))=a√63
Câu 9: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó, khoảng cách giữa đường thẳng BD và mặt phẳng (CB'D') bằng
A. a√22
B. 2a√33
C. a√33
D. a√63
Đáp án: C
Giải thích:
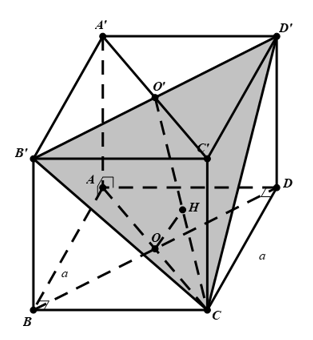
Gắn hệ trục tọa độ như hình vẽ
A(0;0;0); B(1;0;0); D(0;1;0);
A'(0;0;1);C(1;1;0); B'(1;0;1);
D'(0;1;1); C'(1;1;1)
→CB'=(0;−1;1); →CD'=(−1;0;1)
Viết phương trình mặt phẳng (CB'D')
Có VTPT →n=[→CB';→CD']=(−1;−1;−1)
(CB'D'):
1(x−1)+1(y−1)+1(z−0)=0
⇔x+y+z−2=0
d(BD;(CB'D'))=d(B;(CB'D'))
=|1+0+0−2|√12+12+12=1√3=√33
Vậy d(BD;(CB'D'))=a√33.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với AB=2a√3;BC=2a. Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60∘. Khoảng cách từ D đến (SBC) tính theo a bằng
A. a√155
B. 2a√155
C. 4a√155
D. 3a√155
Đáp án: C
Giải thích:
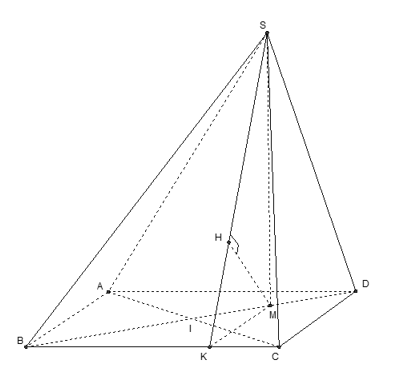
Đặc điểm của hình: Góc giữa SB tạo với mặt phẳng (ABCD) là ^SBM=60∘.
BM=34BD=3a;
SM=BM.tan600=3√3a
Xác định khoảng cách:
d(D,(SBC))=43d(M,(SBC))
=43MH
Tính khoảng cách MH:
1MH2=1MK2+1MS2=1(34.2√3a)2+1(3√3a)2=527a2
MH=√275a .vậy
d(D,(SBC))=43d(M,(SBC))=43MH=4√155a
Câu 11: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB=a, AC=2a, SA vuông góc với mặt phẳng (ABCD), SC tạo với mặt phẳng (SAB) một góc 30∘. Gọi M là một điểm trên cạnh AB sao cho BM=3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM) là
A. √34a51.
B. 2√34a51.
C. 3√34a51.
D. 4√34a51.
Đáp án: B
Giải thích:
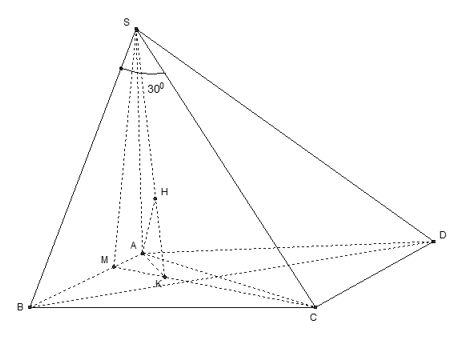
Đặc điểm của hình: SC tạo với mặt phẳng (SAB)góc ^CSB=30∘.
BC=√3a; SB=BC.tan300=a; MC=√(3a4)2+3a2=√574a;
MA=a4;AC=2a; AS=2√2a; AK=2SAMCMC=√1919a
Xác định khoảng cách: d(A,(SBC))=AH
Tính 1AH2=1AK2+1AS2
=1(√1919a)2+1(2√2a)2=1538a2
Vậy d(A,(SBC))=AH=2√3451
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N và P lần lượt là trung điểm của các cạnh AB,AD và DC. Gọi H là giao điểm của CN và DM, biết SH vuông góc (ABCD), SH=a√3. Khoảng cách từ điểm C đến mặt phẳng (SBP) tính theo a bằng
A. a√24
B. a√32
C. a√34
D. a√22
Đáp án: C
Giải thích:
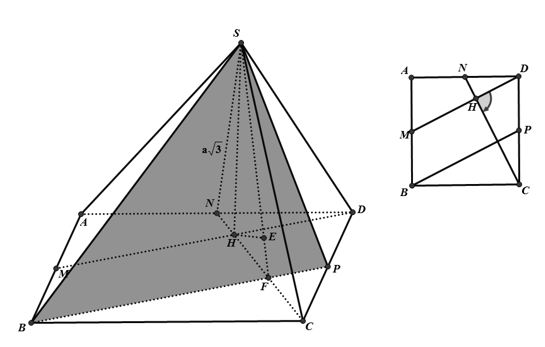
Ta chứng minh: NC⊥MD
Thật vậy: ΔADM=ΔDCM vì
ˆA=ˆD=900;
mà
Ta có:
Kẻ
Do
Mà .
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân có hai đường chéo AC, BD vuông góc với nhau, . Hai mặt phẳng cùng vuông góc với mặt đáy Góc giữa hai mặt phẳng bằng Khoảng cách từ M là trung điểm đoạn AB đến mặt phẳng là
A.
B.
C.
D.
Đáp án: D
Giải thích:
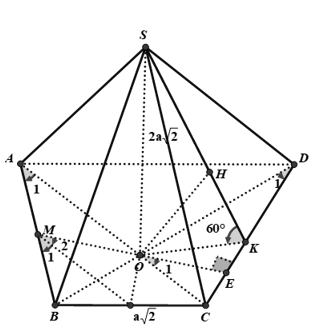
Do
Dựng góc giữa :
. Kẻ
Kéo dài MO cắt DC tại E
Ta có:
Ta có:
.
Câu 14: Tìm mệnh đề sai trong các mệnh đề sau đây?
A. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt phẳng này đến mặt phẳng kia.
B. Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường vuông góc chung của chúng nằm trong mặt phẳng (a) chứa đường này và (a) vuông góc với đường kia.
C. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc (a) chứa a và song song với b đến một điểm N bất kì trên b.
D. Khoảng cách giữa đường thẳng a và mặt phẳng (a) song song với a là khoảng cách từ một điểm A bất kì thuộc a tới mặt phẳng (a)
Đáp án: A
Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
B. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó
C. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia
D. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.
Đáp án: D
Giải thích:
Đáp án A: Đúng
Đáp án B: Sai, do phát biểu này thiếu yếu tố cắt nhau.
Đáp án C: Sai, vì mặt phẳng đó chưa chắc đã tồn tại.
Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc.
Câu 16: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường thẳng vuông góc chung của chúng nằm trong mặt phẳng (P) chứa đường thẳng này và vuông góc với đường thẳng kia.
B. Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm A bất kỳ thuộc a tới mp(P).
C. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt phẳng (P) chứa a và song song với b đến một điểm N bất kỳ trên b.
D. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt phẳng này đến mặt phẳng kia.
Đáp án: C
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S, hình chiếu vuông góc của S lên mặt phẳng là điểm H thuộc cạnh AD sao cho Gọi M là trung điểm của cạnh AB .Biết rằng và đường thẳng SC tạo với mặt đáy một góc Khoảng cách từ M đến mặt phẳng tính theo a bằng
A.
B.
C.
D.
Đáp án: D
Giải thích:
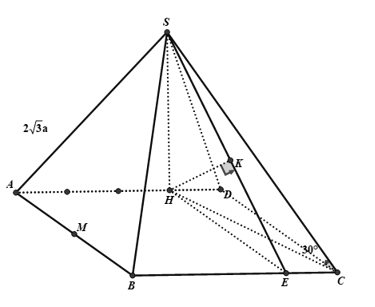
SC có hình chiếu vuông góc lên mp là HC
Đặt
Ta có :
Mà :
Kẻ
Kẻ
Câu 18: Cho hình lập phương cạnh a. Khoảng cách từ A đến bằng
A.
B.
C.
D.
Đáp án: C
Giải thích:
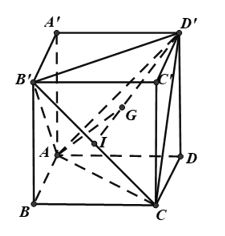
Ta có:
Nên tứ diện là tứ diện đều.
Gọi I là trung điểm , G là trọng tâm tam giác .
Khi đó ta có:
Vì tam giác đều nên
.
Theo tính chất trọng tâm ta có:
.
Trong tam giác vuông có:
.
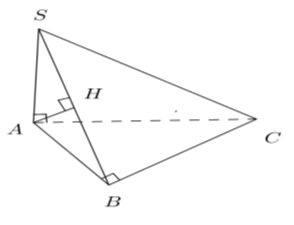
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A với Mặt bên chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc Tính khoảng cách từ điểm S đến mặt phẳng đáy .
A.
B.
C.
D.
Đáp án: A
Giải thích:
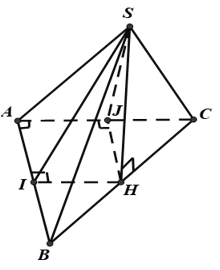
Gọi H là hình chiếu của S lên , vì mặt bên vuông góc với nên
Dựng , theo đề bài ta có
Do đó tam giác (cạnh góc vuông - góc nhọn)
Suy ra .
Lại có
Vậy H trùng với trung điểm của BC.
Từ đó ta có HI là đường trung bình của tam giác ABC nên .
Tam giác SHI vuông tại H và có
vuông cân.
Do đó: .
Câu 20: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng b, cạnh đáy bằng d, với Hãy chọn khẳng định đúng trong các khẳng định bên dưới.
A.
B.
C.
D.
Đáp án: C
Giải thích:
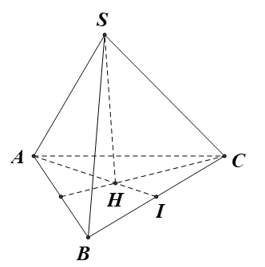
Gọi I là trung điểm của BC, H là trọng tâm tam giác ABC.
Do S.ABC là hình chóp đều nên
Ta có
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên SD. Chọn khẳng định đúng trong các khẳng định sau?
A. Đoạn vuông góc chung của AC và SD là AK
B. Đoạn vuông góc chung của AC và SD là CD
C. Đoạn vuông góc chung của AC và SD là OH
D. Các khẳng định trên đều sai
Đáp án: D
Giải thích:
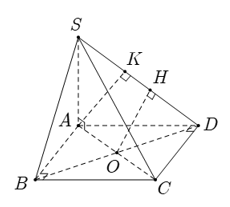
Nếu
(vì
có 2 góc vuông (vô lý).
Theo tính chất của hình vuông .
Nếu
có 2 góc vuông (vô lý)
Như vậy
Câu 22: Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.
A.
B.
C.
D.
Đáp án: C
Giải thích:
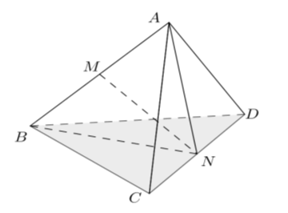
Gọi M, N lần lượt là trung điểm của AB và CD.
Khi đó nên tam giác ANB cân, suy ra .
Chứng minh tương tự ta có , nên .
Ta có:
(p là nửa chu vi)
Mặt khác:
Cách khác. Tính
.
Câu 23: Cho hình chóp S.ABCD có , đáy ABCD là hình chữ nhật với và . Tính khoảng cách giữa SD và BC.
A.
B.
C.
D.
Đáp án: D
Giải thích:
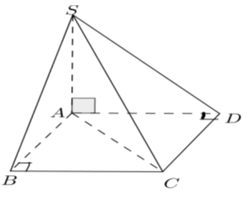
Ta có: BC //
Mà
Ta có:
Câu 24: Cho hình lập phương có cạnh bằng a. Khoảng cách giữa và AC bằng:
A.
B.
C.
D.
Đáp án: C
Giải thích:
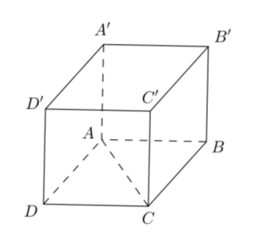
Ta có:
Câu 25: Cho hình lập phương có cạnh bằng 1 (đvdt). Khoảng cách giữa và bằng:
A.
B.
C.
D.
Đáp án: B
Giải thích:
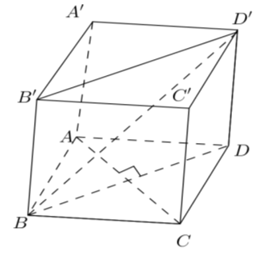
Ta có:
Câu 26: Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai cạnh đối AB và CD bằng
A.
B.
C.
D.
Đáp án: A
Giải thích:
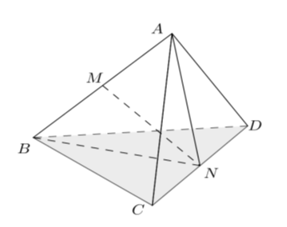
Gọi M, N lần lượt là trung điểm của AB và CD.
Khi đó nên tam giác ANB cân, suy ra .
Chứng minh tương tự ta có , nên .
Ta có:
(p là nửa chu vi)
Mặt khác:
Câu 27: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao Khoảng cách từ điểm O đến cạnh bên SA bằng
A.
B.
C.
D.
Đáp án: B
Giải thích:
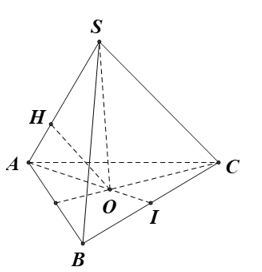
Vì hình chóp S.ABC đều có SO là đường cao
O là tâm của
Gọi I là trung điểm cạnh BC.
Tam giác ABC đều nên
.
Kẻ
Xét tam giác SOA vuông tại O :
Câu 28: Cho hình lập phương cạnh bằng a. Gọi M là trung điểm của AD. Khoảng cách từ đến mặt phẳng bằng bao nhiêu?
A.
B.
C.
D. a
Đáp án: A
Giải thích:
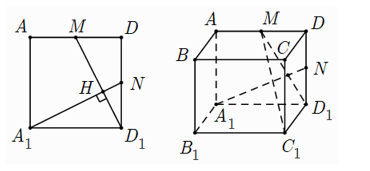
Gọi N là trung điểm cạnh và
Khi đó ta chứng minh được
suy ra
Câu 29: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng cạnh bên bằng 3a. Khoảng cách từ S đến mặt phẳng bằng:
A. 4a
B. 3a
C. a
D. 2a
Đáp án: C
Giải thích:
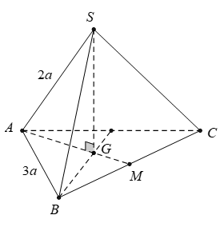
Gọi G là trọng tâm tam giác ABC. Do S.ABC là chóp đều nên .
vuông tại G
Câu 30: Cho hình lăng trụ tứ giác đều có cạnh đáy bằng a. Gọi M,N,P lần lượt là trung điểm của AD,DC,. Tính khoảng cách giữa hai mặt phẳng và .
A.
B.
C.
D.
Đáp án: D
Giải thích:
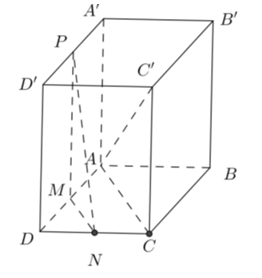
Ta có: //
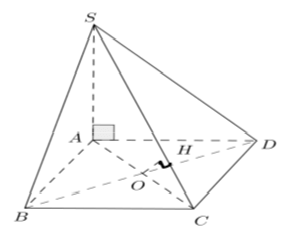
Câu 31: Cho hình chóp S. ABCD có SA ⊥ (ABCD) ; SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
Đáp án: A
Giải thích:
Chọn A
+ Kẻ OH ⊥ SC , khi đó d(O; SC) = OH
+ Ta có: ΔSAC ∼ ΔOHC (g.g) (g-g) nên
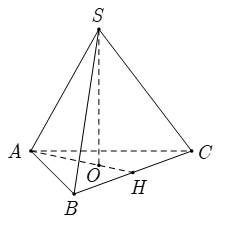
Câu 32: Hình chóp đều S.ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC) bằng :
A. 2a
B. a√3
C. a
D. a√5
Đáp án: C
Giải thích:
+ Gọi O là trọng tâm tam giác ABC.Do tam giác ABC đều nên O là tâm đường tròn ngoại tiếp tam giác ABC
+ Ta có: SA = SB = SC và OA = OB = OC nên SO là trục đường tròn ngoại tiếp tam giác ABC. Do đó SO ⊥ (ABC)
Chọn đáp án C
Câu 33: Cho hình chóp S.ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết SA = a√3, AB = a√3 . Khoảng cách từ A đến (SBC) bằng:
Đáp án: A
Giải thích:
Chọn D
Kẻ AH ⊥ SB
Ta có:
Lại có: AH ⊥ SB nên AH ⊥ (SBC)
⇒ d(A; (SBC)) = AH
Trong tam giác vuông SAB ta có:
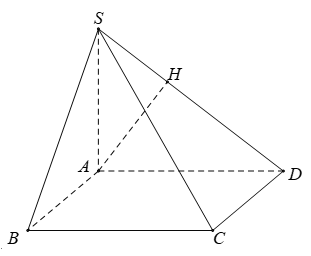
Câu 34: Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật. Biết AD = 2a; SA = a . Khoảng cách từ B đến (SCD) bằng:
Đáp án: C
Giải thích:
Ta có; AB // CD nên d(B, (SCD))= d(A; (SCD)).
Ta tính khoảng cách từ A đến (SCD) :
SA ⊥ (ABCD) nên SA ⊥ CD; AD ⊥ CD
Suy ra (SAD) ⊥ CD
Trong (SAD) kẻ AH vuông góc SD tại H .
Khi đó AH ⊥ (SCD)
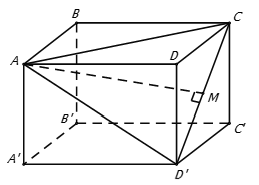
Câu 35: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD’ bằng
Đáp án: B
Giải thích:
Gọi M là trung điểm của CD’
Do ABCD.A’B’C’D’ là hình lập phương nên tam giác ACD’ là tam giác đều cạnh a√2 .
+ Tam giác ACD’ có AM là đường trung tuyến nên đồng thời là đường cao AM ⊥ CD'.
d(A; CD’) = AM = AC.sin(ACM) = a√2.sin60°= (a√6)/2
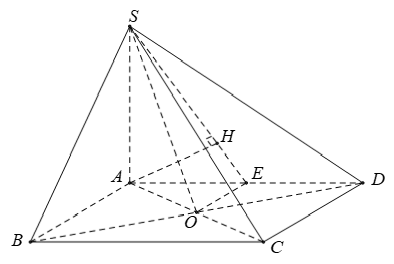
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√2. Gọi E là trung điểm AD. Khoảng cách giữa AB và (SOE) là
Đáp án: B
Giải thích:
+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy .
mà (SAB) ∩ (SAD) = SA
⇒ SA ⊥ (ABCD) .
+ Do E là trung điểm của AD khi đó
Tam giác ABD có EO là đường trung bình
⇒ EO // AB ⇒ AB // (SOE)
⇒ d(AB, (SOE)) = d(A; (SOE)) = AH
với H là hình chiếu của A lên SE.
Câu 37: Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách giữa (SDA) và BC?
Đáp án: D
Giải thích:
+ Ta có: BC // AD nên BC // (SAD)
⇒ d(BC; (SAD)) = d(B; SAD))
+ Ta chứng minh BA ⊥ (SAD) :
Do BA ⊥ AD (vì ABCD là hình chữ nhật)
Và BA ⊥ SA (vì SA ⊥ (ABCD))
⇒ BA ⊥ (SAD)
⇒ d(B; (SAD)) = BA
Áp dụng định lí Pytago trong tam giác vuông ABC có:
AB2 = AC2 - BC2 = 5a2 - 2a2 = 3a2
⇒ AB = √3 a
⇒ d(CB; (SAD)) = AB = √3 a
Câu 38: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; AB= a cạnh bên SA vuông góc với đáy và SA = a√2. Gọi M và N lần lượt là trung điểm của AB; AC. Khoảng cách giữa BC và (SMN) bằng bao nhiêu?
Đáp án: A
Giải thích:
+ Tam giác ABC có MN là đường trung bình nên MN // BC
⇒ BC // (SMN) nên :
d(BC; (SMN)) = d(B; (SMN)) = d(A; (SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
+ Ta chứng minh: MN ⊥ (SAM):
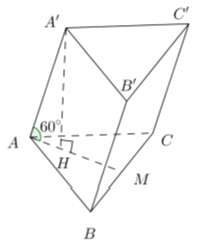
Câu 39: Cho hình lăng trụ tam giác ABC.A’B’C’ có các cạnh bên hợp với đáy những góc bằng 60°, đáy ABC là tam giác đều và A’ cách đều A, B; C. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Đáp án: A
Giải thích:
+ Vì tam giác ABC đều và AA’ = BA’ = CA’ (giả thiết) nên A’.ABC là hình chóp đều.
Gọi A’H là chiều cao của lăng trụ, suy ra H là trọng tâm tam giác ABC
Lăng trụ ABC.A’B’C’ có các cạnh bên hợp với đáy góc 60° nên ∠A'AH = 60°.
+ Xét tam giác AHA’ có: A'H = AH.tan60° = ((a√3)/3).√3 = a
+ lại có; (ABC) // (A’B’C’) ( định nghĩa hình lăng trụ) nên d((ABC), (A’B’C’)) = d( A’, (ABC)) = A’H = a
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O; SA vuông góc với đáy (ABCD). Gọi K; H theo thứ tự là hình chiếu vuông góc của A và O lên SD Chọn khẳng định đúng trong các khẳng định sau?
A. Đoạn vuông góc chung của AC và SD là AK
B. Đoạn vuông góc chung của AC và SD là CD
C. Đoạn vuông góc chung của AC và SD là OH
D. Các khẳng định trên đều sai
Đáp án: D
Giải thích:
+ Ta xét các phương án:
- Phương án A:
Giả sử AK ⊥ AC, do AK ⊥ AB ⇒ AK ⊥ (ABC)
⇒ AK ≡ SA ( vì SA ⊥ (ABC)) ⇒ SA ⊥ SD ⇒ ΔSAD có 2 góc vuông (vô lý)
- Phương án B:
Theo tính chất của hình vuông thì AC và CD không vuông góc với nhau nên đoạn vuông góc chung của AC và SD không phải CD.
- Phương án C:
Giả sử AC ⊥ OH, do AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SO
Lại có: SA ⊥ AC ⇒ vô lý.
⇒ Đoạn vuông góc chung của AC và SD không phải là OH.
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Vectơ trong không gian có đáp án
Trắc nghiệm Hai đường thẳng vuông góc có đáp án
Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án