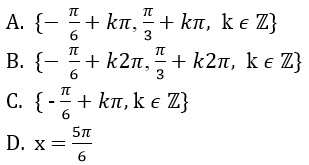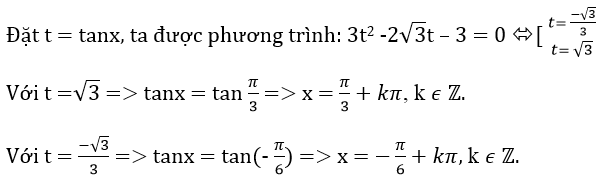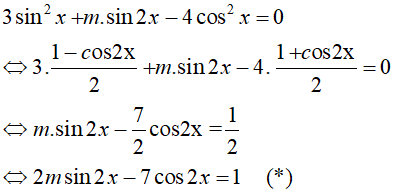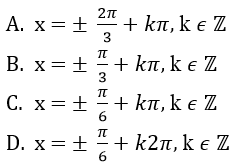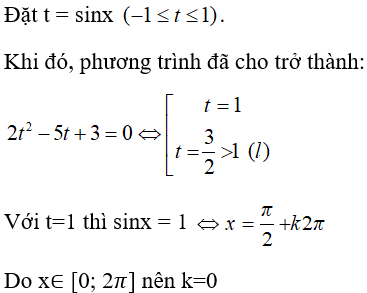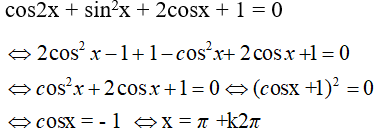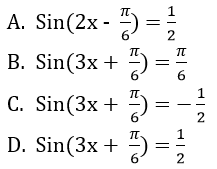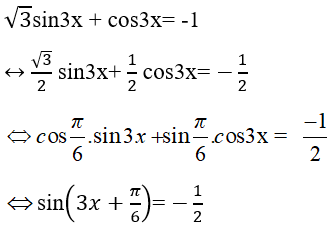TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án 2023) – Toán 11

Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 2: Phương trình lượng giác cơ bản có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 2.

1 4,927 12/01/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản

Bài giảng Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản

Câu 1: Tìm số nghiệm thuộc đoạn $[2 π; 4 π]$ của phương trình $\frac{\sin 3 x}{\cos x + 1} = 0$

A. 6

B. 5

C. 4

D. 3

Hiển thị đáp án

Đáp án: A

Giải thích:

$\frac{\sin 3 x}{\cos x + 1} = 0$

$\Leftrightarrow \{\begin{cases} \cos x + 1 \neq 0 \\ \sin 3 x = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq π + k 2 π \\ x = \frac{k π}{3} \end{cases}, k \in ℤ$

Do $x \in [2 π; 4 π]$ nên

$x \in \{2 π; \frac{7 π}{3}; \frac{8 π}{3}; \frac{10 π}{3}; \frac{11 π}{3}; 4 π\}$

Vậy có 6 nghiệm $x \in [2 π; 4 π]$ .

Câu 2: Khẳng định nào đúng:

A. $\tan x = 1 \Leftrightarrow x = \frac{π}{4} + k 2 π$

B. $\sin 2 x = 0 \Leftrightarrow x = k π$

C. $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k 2 π$

D. $\sin 2 x = 1 \Leftrightarrow x = \frac{π}{4} + k π$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có

$\sin 2 x = 1$

$\Leftrightarrow 2 x = \frac{π}{2} + k 2 π$

$\Leftrightarrow x = \frac{π}{4} + k π (k \in ℤ)$ .

Câu 3: Tìm tất cả các giá trị của tham số m để phương trình $\sqrt{3} \sin x + \cos x = m$ có nghiệm

A. $m \leq 2$

B. $- 2 < m < 2$

C. $m \geq 2$ hoặc $m \leq - 2$

D. $- 2 \leq m \leq 2$

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình có nghiệm khi

${(\sqrt{3})}^{2} + 1^{2} \geq m^{2} \Leftrightarrow m^{2} \leq 4$

$\Leftrightarrow - 2 \leq m \leq 2$ .

Câu 4: Số nghiệm của phương trình lượng giác: $2 \sin x - 1 = 0$ thỏa điều kiện $- π < x < π$ là

A. 4

B. 3

C. 2

D. 1

Hiển thị đáp án

Đáp án: C

Giải thích:

Phương trình $2 \sin x - 1 = 0 \Leftrightarrow \sin x = \frac{1}{2}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}; k \in ℤ$

Do $- π < x < π$ nên $x = \frac{π}{6}; x = \frac{5 π}{6}$ .

Câu 5: Phương trình $m \sin x + 3 \cos x = 5$ có nghiệm khi và chỉ khi

A. $|m| \leq 4$

B. $|m| \geq 4$

C. $m \leq - 4$

D. $m \geq 4$

Hiển thị đáp án

Đáp án: B

Giải thích:

Phương trình đã cho có nghiệm khi và chỉ khi

$m^{2} + 9 \geq 25 \Leftrightarrow |m| \geq 4$

Câu 6: Cho phương trình lượng giác $\sqrt{3} \tan x + 3 = 0$ có nghiệm là

A. $x = - \frac{π}{3} + k 2 π$

B. $x = \frac{π}{3} + k π$

C. $x = \frac{π}{6} + k π$

D. $x = - \frac{π}{3} + k π$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có

$\sqrt{3} \tan x + 3 = 0$

$\Leftrightarrow \tan x = - \sqrt{3}$

$\Leftrightarrow x = - \frac{π}{3} + k π, k \in ℤ$ .

Câu 7: Phương trình: $\cos x - m = 0$ vô nghiệm khi m là

A. $[\begin{array}{l} m < - 1 \\ m > 1 \end{array}$

B. $m > 1$

C. $- 1 \leq m \leq 1$

D. $m < - 1$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $cosx - m = 0$

$\Leftrightarrow c o s x = m$

Phương trình vô nghiệm

$\Leftrightarrow |m| > 1 \Leftrightarrow [\begin{array}{l} m < - 1 \\ m > 1 \end{array}$ .

Câu 8: Phương trình lượng giác: $\cos^{2} x + 2 \cos x - 3 = 0$ có nghiệm là

A. $x = \frac{π}{2} + k 2 π$

B. Vô nghiệm

C. $x = k 2 π$

D. x = 0.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $\cos^{2} x + 2 \cos x - 3 = 0$

$\Leftrightarrow [\begin{array}{l} \cos x = 1 (n) \\ \cos x = - 3 (l) \end{array}$

$\cos x = 1 \Leftrightarrow x = k 2 π$

Câu 9: Phương trình lượng giác: $\cos 3 x = \cos 12 °$ có nghiệm là

A. $x = \frac{π}{45} + \frac{k 2 π}{3}$

B. $x = \frac{- π}{45} + \frac{k 2 π}{3}$

C. $x = \pm \frac{π}{45} + \frac{k 2 π}{3}$

D. $x = \pm \frac{π}{15} + k 2 π$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $12 ° = \frac{π}{15}$

$\cos 3 x = \cos 12 °$

$\Leftrightarrow \cos 3 x = \cos \frac{π}{15}$

$\Leftrightarrow 3 x = \pm \frac{π}{15} + k 2 π$

$\Leftrightarrow x = \pm \frac{π}{45} + \frac{k 2 π}{3}$ .

Câu 10: Một nghiệm của phương trình $\sin^{2} x + \sin^{2} 2 x + \sin^{2} 3 x = 2$ là

A. $\frac{π}{6}$

B. $\frac{π}{3}$

C. $\frac{π}{8}$

D. $\frac{π}{12}$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\sin^{2} x + \sin^{2} 2 x + \sin^{2} 3 x = 2$

$\Leftrightarrow \frac{1 - \cos 2 x}{2} + \frac{1 - \cos 4 x}{2} + \frac{1 - \cos 6 x}{2} = 2$

$\Leftrightarrow \cos 2 x + \cos 4 x + \cos 6 x + 1 = 0$

$\Leftrightarrow 2 \cos x \cos 3 x + 2 \cos^{2} 3 x = 0$

$\Leftrightarrow \cos 3 x (\cos x + \cos 3 x) = 0$

$\Leftrightarrow [\begin{array}{l} \cos 3 x = 0 \\ \cos x + \cos 3 x = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} 3 x = k π \\ \cos x = - \cos 3 x \end{array}$

$\Leftrightarrow [\begin{array}{l} x = k \frac{π}{3} \\ \cos x = \cos (π - 3 x) \end{array}$

$\Leftrightarrow [\begin{array}{l} x = k \frac{π}{3} \\ x = π - 3 x + k 2 π \\ x = 3 x - π + k 2 π \end{array}$

$\Leftrightarrow [\begin{array}{l} x = k \frac{π}{3} \\ x = \frac{π}{4} + k \frac{π}{2} \\ x = \frac{π}{2} - k π \end{array} (k \in ℤ)$

Câu 11: Gọi M, m lần lượt là nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình $2 \sin^{2} x + 3 \cos x - 3 = 0$ . Giá trị của M + m là

A. $- \frac{π}{6}$

B. 0

C. $\frac{π}{6}$

D. $- \frac{π}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

$2 \sin^{2} x + 3 \cos x - 3 = 0$

$\Leftrightarrow 2 (1 - \cos^{2} x) + 3 \cos x - 3 = 0$

$\Leftrightarrow - 2 \cos^{2} x + 3 \cos x - 1 = 0$

$\Leftrightarrow [\begin{array}{l} \cos x = 1 \\ cosx = \frac{1}{2} \end{array}$

$\Leftrightarrow [\begin{array}{l} x = k 2 π \\ x = \pm \frac{π}{3} + k 2 π \end{array} (k \in ℤ)$ .

Câu 12: Phương trình $\sqrt{3} \sin x - \cos x = 1$ tương đương với phương trình nào sau đây

A. $\sin (x - \frac{π}{6}) = \frac{1}{2}$

B. $\sin (\frac{π}{6} - x) = \frac{1}{2}$

C. $\sin (x - \frac{π}{6}) = 1$

D. $\cos (x + \frac{π}{3}) = \frac{1}{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$\sqrt{3} \sin x - \cos x = 1$

$\Leftrightarrow \frac{\sqrt{3}}{2} \sin x - \frac{1}{2} \cos x = \frac{1}{2}$

$\Leftrightarrow \sin (x - \frac{π}{6}) = \frac{1}{2}$ .

Câu 13: Tìm công thức nghiêm của phương trình $\sin x = \sin α$

A. $x = α + k 2 π$ và $x = - α + k 2 π, k \in ℤ$

B. $x = α + k 2 π$ và $x = π - α + k 2 π, k \in ℤ$

C. $x = α + k π$ và $x = - α + k π, k \in ℤ$

D. $x = α + k π$ và $x = π - α + k π, k \in ℤ$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\sin x = \sin α$

$\Leftrightarrow [\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array}; k \in ℤ$ .

Câu 14: Khẳng định nào sau đây sai?

A. $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k 2 π (k \in ℤ)$

B. $\cos x = 1 \Leftrightarrow x = k 2 π (k \in ℤ)$

C. $\sin x = 1 \Leftrightarrow x = \frac{π}{2} + k 2 π (k \in ℤ)$

D. $\sin x = - 1 \Leftrightarrow x = - \frac{π}{2} + k 2 π (k \in ℤ)$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\cos x = 0$

$\Leftrightarrow x = \frac{π}{2} + k π (k \in ℤ)$ .

Câu 15: Phương trình $\cos x = - \frac{\sqrt{3}}{2}$ có tập nghiệm là

A. $\{x = \pm \frac{π}{3} + k π, k \in ℤ\}$

B. $\{x = \pm \frac{π}{6} + k π, k \in ℤ\}$

C. $\{x = \pm \frac{5 π}{6} + k 2 π, k \in ℤ\}$

D. $\{x = \pm \frac{π}{3} + k 2 π, k \in ℤ\}$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\cos x = - \frac{\sqrt{3}}{2}$

$\Leftrightarrow x = \pm \frac{5 π}{6} + k 2 π; k \in ℤ$ .

Câu 16: Nghiệm của phương trình $\sin x = \frac{\sqrt{3}}{2}$ là

A. $[\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}$

B. $[\begin{array}{l} x = \frac{π}{3} + k 2 π \\ x = \frac{2 π}{3} + k 2 π \end{array}$

C. $[\begin{array}{l} x = \frac{π}{3} + k π \\ x = \frac{2 π}{3} + k π \end{array}$

D. $x = \pm \frac{π}{3} + k 2 π$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\sin x = \frac{\sqrt{3}}{2}$

$\Leftrightarrow \sin x = \sin \frac{π}{3}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{3} + k 2 π \\ x = \frac{2 π}{3} + k 2 π \end{array}$ .

Câu 17: Phương trình lượng giác $2 \cos x + \sqrt{2} = 0$ có nghiệm là

A. $[\begin{array}{l} x = \frac{7 π}{4} + k 2 π \\ x = - \frac{7 π}{4} + k 2 π \end{array}$

B. $[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = \frac{3 π}{4} + k 2 π \end{array}$

C. $[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = - \frac{π}{4} + k 2 π \end{array}$

D. $[\begin{array}{l} x = \frac{3 π}{4} + k 2 π \\ x = - \frac{3 π}{4} + k 2 π \end{array}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$2 \cos x + \sqrt{2} = 0$

$\Leftrightarrow \cos x = - \frac{\sqrt{2}}{2} = \cos \frac{3 π}{4}$

$\Leftrightarrow [\begin{array}{l} x = \frac{3 π}{4} + k 2 π \\ x = - \frac{3 π}{4} + k 2 π \end{array}$ .

Câu 18: Giải phương trình $\cos (2 x + \frac{π}{4}) = 1$

A. $x = - \frac{π}{8} + k 2 π (k \in ℤ)$

B. $x = - \frac{π}{8} + k π (k \in ℤ)$

C. $x = \pm \frac{π}{8} + k π (k \in ℤ)$

D. $x = - \frac{π}{4} + k π (k \in ℤ)$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\cos (2 x + \frac{π}{4}) = 1$

$\Leftrightarrow x + \frac{π}{4} = k 2 π; k \in ℤ$

$\Leftrightarrow x = - \frac{π}{8} + k π, k \in ℤ$ .

Câu 19: Tập tất cả các giá trị của tham số m để phương trình $\sin x = m + 1$ có nghiệm

A. $m \in [- 1; 1]$

B. $m \in [- 2; 2]$

C. $m \in [- 2; 0]$

D. $m \in [0; 2]$

Hiển thị đáp án

Đáp án: C

Giải thích:

Để phương trình $\sin x = m + 1$ có m thì

$|m + 1| \leq 1$

$\Leftrightarrow - 1 \leq m + 1 \leq 1$

$\Leftrightarrow - 2 \leq m \leq 0$ .

Câu 20: Họ nghiêm của phương trình $\cot (x - \frac{π}{6}) = \frac{\sqrt{3}}{3}$ là

A. $x = - \frac{π}{3} + k π$

B. $x = \frac{π}{6} + k π$

C. $x = \frac{π}{2} + k π$

D. $x = \frac{π}{3} + k 2 π$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\cot (x - \frac{π}{6}) = \frac{\sqrt{3}}{3}$

$\Leftrightarrow x - \frac{π}{6} = \frac{π}{3} + k π$

$\Leftrightarrow x = \frac{π}{2} + k π, k \in ℤ$ .

Câu 21: Tìm số nghiệm của phương trình $\cos 3 x = 1$ thỏa mãn $x \in [0; π]$

A. 4

B. 2

C. 1

D. 3

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $\cos 3 x = 1$

$\Leftrightarrow 3 x = k 2 π$

$\Leftrightarrow x = \frac{k 2 π}{3}$

Theo yêu cầu bài toán thì

$0 \leq \frac{k 2 π}{3} \leq π$

$\Leftrightarrow 0 \leq k \leq \frac{3}{2}$

Chọn $k = 0; k = 1$ .

Câu 22: Tìm tất cả các giá trị của m để phương trình $1 + \cos x = m$ có đúng hai nghiệm $x \in (\frac{π}{2}; \frac{3 π}{2})$

A. $0 \leq m < 1$

B. $0 < m < 1$

C. $- 1 \leq m \leq 1$

D. $- 1 < m < 0$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $1 + \cos x = m$

$\Leftrightarrow \cos x = m - 1$

Để phương trình có đúng 2 nghiệm $x \in (\frac{π}{2}; \frac{3 π}{2})$ thì

$- 1 < \cos x < 0$

$\Leftrightarrow - 1 < m - 1 < 0$

$\Leftrightarrow 0 < m < 1$ .

Câu 23: Số nghiệm của phương trình $\frac{\sin 3 x}{\cos x + 1} = 0$ thuộc đoạn $[2 π, 4 π]$ là

A. 4

B. 5

C. 6

D. 7

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $\frac{\sin 3 x}{\cos x + 1} = 0$

$\Leftrightarrow \{\begin{cases} c o x \neq - 1 \\ \sin 3 x = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq π + k 2 π \\ 3 x = k π \end{cases}$

$x \in [2 π; 4 π]$

$\Leftrightarrow 2 π \leq l \frac{π}{3} \leq 4 π$

$\Leftrightarrow 6 \leq l \leq 12$

Vậy số nghiệm thỏa mãn điều kiện của l là

$\{2 π; \frac{7}{3} π; \frac{8}{3} π; 3 π; \frac{10}{3} π; \frac{11}{3} π; 4 π\}$ ,

so với điều kiện loại nghiệm $3 π$ .

Câu 24: Giải phương trình $\tan (4 x - \frac{π}{3}) = - \sqrt{3}$

A. $x = \frac{π}{3} + k \frac{π}{3}, k \in ℤ$

B. $x = \frac{π}{3} + k π, k \in ℤ$

C. $x = \frac{π}{2} + k π, k \in ℤ$

D. $x = k \frac{π}{4}, k \in ℤ$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\tan (4 x - \frac{π}{3}) = - \sqrt{3}$

$\Leftrightarrow \tan (4 x - \frac{π}{3}) = \tan (- \frac{π}{3})$

$\Leftrightarrow 4 x - \frac{π}{3} = - \frac{π}{3} + k π$

$\Leftrightarrow x = k \frac{π}{4} (k \in ℤ)$ .

Câu 25: Phương trình $\sin 2 x \cos 2 x \cos 4 x = 0$ có nghiệm là

A. $k π, k \in ℤ$

B. $k \frac{π}{4}; k \in ℤ$

C. $k \frac{π}{2}; k \in ℤ$

D. $k \frac{π}{8}; k \in ℤ$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\sin 2 x \cos 2 x \cos 4 x = 0$

$\Leftrightarrow \frac{1}{2} \sin 4 x \cos 4 x = 0$

$\Leftrightarrow \frac{1}{4} \sin 8 x = 0$

$\Leftrightarrow 8 x = k π, k \in ℤ$

hay $x = k \frac{π}{8}, k \in ℤ$ .

Câu 26: Tập xác định của hàm số $y = \frac{1}{\sin x - \cos x}$ là

A. $D = ℝ \ \{\frac{π}{4} + k 2 π\}, k \in ℤ$

B. $D = ℝ \ \{\frac{π}{2} + k π\}, k \in ℤ$

C. $D = ℝ \ \{k π\}, k \in ℤ$

D. $D = ℝ \ \{\frac{π}{4} + k π\}, k \in ℤ$

Hiển thị đáp án

Đáp án: D

Giải thích:

Điều kiện: $\sin x - \cos x \neq 0$

$\Leftrightarrow \tan x \neq 1$

$\Leftrightarrow x \neq \frac{π}{4} + k π; k \in ℤ$

Tập xác định của hàm số là $D = ℝ \ \{\frac{π}{4} + k π\}; k \in ℤ$

Câu 27: Điều kiện xác định của hàm số $y = \frac{1 - \sin x}{\cos x}$ là

A. $x \neq \frac{π}{2} + k π$

B. $x \neq \frac{π}{2} + k 2 π$

C. $x \neq k π$

D. $x \neq - \frac{π}{2} + k 2 π$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số xác định $\Leftrightarrow \cos x \neq 0$

$\Leftrightarrow x \neq \frac{π}{2} + k π$ .

Câu 28: Với giá trị nào của m thì phương trình $\cos (\frac{x}{3} + 2) + \frac{3}{2} = m$ vô nghiệm?

A. $m \in (- \infty; - \frac{5}{2}) \cup (- \frac{1}{2}; + \infty)$

B. $m \in (- \infty; \frac{1}{2}) \cup (\frac{5}{2}; + \infty)$

C. $y = \cos x$

D. $m < - \frac{1}{2}$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\cos (\frac{x}{3} + 2) + \frac{3}{2} = m$

$\Leftrightarrow \cos (\frac{x}{3} + 2) = m - \frac{3}{2}$

Phương trình vô nghiệm

$\Leftrightarrow |m - \frac{3}{2}| > 1$

$\Leftrightarrow [\begin{array}{l} m > \frac{5}{2} \\ m < \frac{1}{2} \end{array}$ .

Câu 29: Nghiệm của phương trình 2cos²x + 3sinx – 3 = 0 thuộc (0; π/2) là:

A. x = π/3

B. x = π/4

C. x = π/6

D. x = 5 π/6

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 30: Tập nghiệm của phương trình: 3sin²x - 2√3sinxcosx - 3cos²x = 0 là:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: A

Giải thích:

- Nếu cosx = 0 phương trình trở thành 3sin²x = 0 ⇒ sinx = 0(vô lí) vì khi cosx = 0 thì sin2x = 1 nên sinx = ±1.

- Nếu cosx ≠ 0, chia cả hai vế của phương trình cho cos²x, ta được:

3tan2x - 2√3tanx – 3 = 0

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 31: Tổng các nghiệm của phương trình:

sin²(2x - π/4) - 3cos(3 π/4 -2x)+ 2 = 0 (1) trong khoảng (0;2π) là:

A. 7π/8

B. 3π/8

C. π

D. 7π/4

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 32. Điều kiện để phương trình 3sinx + mcosx = 5 vô nghiệm là:

A. $[\begin{matrix} \begin{matrix} m \leq - 4 \\ m \geq 4 \end{matrix} \end{matrix}$

B. m > 4

C. m < - 4

D. -4 < m < 4

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình 3sinx + mcosx= 5 vô nghiệm khi:

3²+ m² < 5² ↔ m² < 16 ↔ -4 < m < 4

Câu 33: Phương trình 3sin²x + msin2x – 4cos²x = 0 có nghiệm khi:

A. m = 4

B. m ≥ 4

C. m ≤ 4

D. m ∈R

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Phương trình đã cho có nghiệm khi và chỉ khi (*) có nghiệm.

Do đó: 4m² + 49 ≥ 1 ⇔ 4m² + 48 ≥ 0 ( luôn đúng )

Vậy phương trình đã cho luôn có nghiệm với mọi m.

Câu 34: Nghiệm dương bé nhất của phương trình 2sin²x – 5sinx + 3 = 0 là:

A. x = π/6

B. x = π/2

C. x = 5π/2

D. x = 5π/6

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 35: Phương trình cos²2x + cos2x - 3/4 = 0 có nghiệm khi:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 36: Số nghiệm của phương trình 2sin²x – 5sinx + 3 = 0 thuộc [0; 2π] là:

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 37: Số nghiệm của phương trình cos2x + sin²x + 2cosx + 1= 0 thuộc [0; 4π] là:

A. 1

B. 2

C. 4

D. 6

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Các nghiệm của phương trình thuộc đoạn [0; 4π] là: π; 3π

Câu 38: Phương trình (2 – a)sinx + (1+ 2a)cosx = 3a – 1 có nghiệm khi:

A. $[\begin{matrix} \begin{matrix} \begin{matrix} a \geq 2 \\ a \leq \frac{- 1}{2} \end{matrix} \end{matrix} \end{matrix}$

B. $[\begin{matrix} \begin{matrix} \begin{matrix} a \geq \frac{1}{2} \\ a \leq - 2 \end{matrix} \end{matrix} \end{matrix}$

C. $\frac{- 1}{2} \leq a \leq 2$

D. $- 1 \leq a \leq \frac{1}{2}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Phương trình đã cho có nghiệm khi và chỉ khi

(2 – a)² + (1 +2a)² ≥ (3a – 1)²

⇔ 4 - 4a + a² + 1 + 4a + 4a² ≥ 9a² - 6a + 1

⇔ 4a² – 6a – 4 ≤ 0 ⇔ (-1)/2 ≤ a ≤ 2.

Câu 39: Phương trình √3sin3x + cos3x = - 1 tương đương với phương trình nào sau đây?

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 40: Phương trình cos²2x + cos2x - 3/4 = 0 có nghiệm khi:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Một số phương trình lượng giác thường gặp có đáp án

Trắc nghiệm Ôn tập chương 1 có đáp án

Trắc nghiệm Quy tắc đếm có đáp án

Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp có đáp án

Trắc nghiệm Nhị Thức Newton có đáp án

1 4,927 12/01/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3