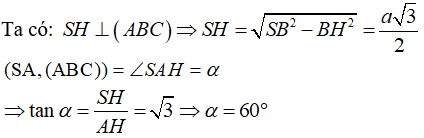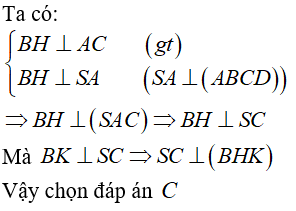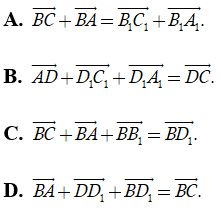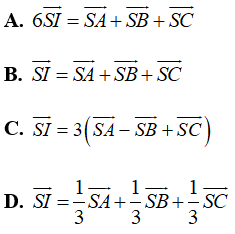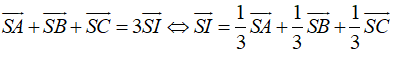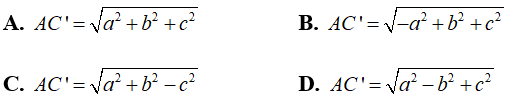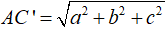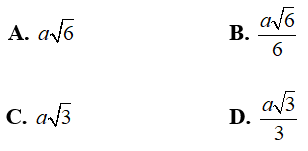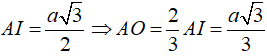TOP 40 câu Trắc nghiệm Bài tập ôn tập chương 3 (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài tập ôn tập chương 3 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài Ôn tập chương 3.
Trắc nghiệm Toán 11 Bài: Ôn tập chương 3
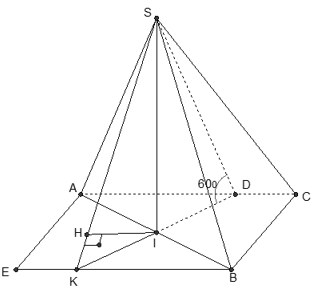
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a;AD=2a(a>0). Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy .Biết mặt phẳng (SAC) hợp với (ABCD) một góc 60o . tính khoảng cách giữa CD và SB.
A. 2a√35
B. 2a√315
C. a√315
D. 3a√35
Đáp án: A
Giải thích:
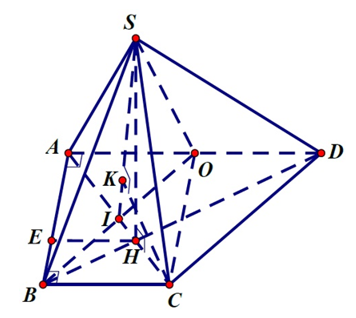
Gọi H=AC∩BD⇒SH⊥(ABCD) và BH=13BD
Kẻ HE⊥AB ⇒AB⊥(SHE) hay
((SAB);(ABCD))=^SEH=60o
Mà HE=13AD=2a3⇒SH=2a√33
Gọi O là trung điểm của AD, ta có ABCD là hình vuông cạnh a
⇒ΔACD có trung tuyến ;
CO=12AD; CD⊥AC
CD⊥(SAC)và BO//CD
hay CD//(SBO) và BO⊥(SAC)
suy ra
d(CD;SB)=d(CD;(SBO))
=d(C;(SBO)).
Tính chất trọng tâm tam giác BCO
⇒IH=13IC=a√26
⇒IS=√IH2+HS2=5a√26
Kẻ CK⊥SI mà CK⊥BO⇒CK⊥(SBO)
⇒d(C;(SBO))=CK
Trong tam giác SIC có
SSIC=12SH.IC=12SI.CK
⇒CK=SH.ICSI=2a√35
Vậy d(CD;SB)=2a√35.
Câu 2. Cho hình chóp SABCD có đáy là hình bình hành với AB=2a,BC=a√2;BD=a√6. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác BCD, biết SG = 2a. Khoảng cách giữa hai đường thẳng AC và SB theo a là:
A. a
B. 2a
C. a2
D. a3
Đáp án: A
Giải thích:
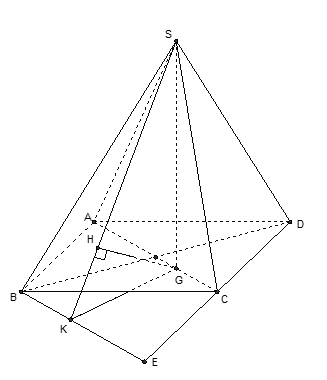
Ta có ABCD là hình bình hành, AB = 2a, BC = a√2, BD =a√6 nên ABCD là hình chữ nhật.
Dựng hình bình hành ACEB.
Ta có AC∥BE, AC ⊄
mà
vậy
.
Dựng lại có nên
Dựng
lại có nên
Ta có .
Tam giác ABC vuông tại B
suy ra
vậy .
Xét tam giác SGK vuông tại G,
đường cao có
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 4a , BC = 3a, gọi I là trung điểm của AB hai mặt phẳng và cùng vuông góc với góc giữa hai mặt phẳng bằng . Khoảng cách giữa hai đường thẳng SB và AC theo a là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Ta có cùng vuông góc với mặt phẳng nên .
Dựng hình bình hành ACBE.
Ta có
mà vậy
.
Dựng
lại có nên .
Dựng
lại có nên
Kéo dài IK cắt AC tại D mà
Lại có
.
Góc giữa và bằng suy ra .
Ta có
Mà tam giác ABC vuông tại B suy ra
vậy .
Xét tam giác SID vuông tại I,
,suy ra
Xét tam giác SIK vuông tại I, đường cao IH có
Câu 4: Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng α. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
A.
B.
C.
D.
Đáp án: D
Giải thích:
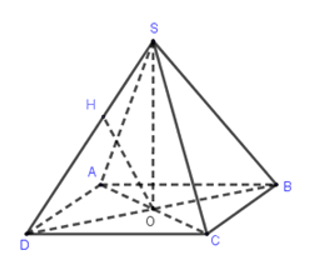
SO⊥(ABCD), O là tâm của hình vuông ABCD.
Kẻ OH⊥SD, khi đó d(O;SD)=OH, α=
OD=
Câu 5: Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết SA = 3a, AB = , BC = . Khoảng cách từ B đến SC bằng
A.
B. 2a
C.
D.
Đáp án: B
Giải thích:
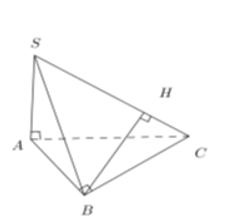
Vì SA, AB, BC vuông góc với nhau từng đôi một nên CB⊥SB
Kẻ BH⊥SC, khi đó d(B;SC)=BH
Ta có: SB=
Trong tam giác vuông SBC ta có:
Câu 6: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng
A.
B.
C.
D.
Đáp án: B
Giải thích:
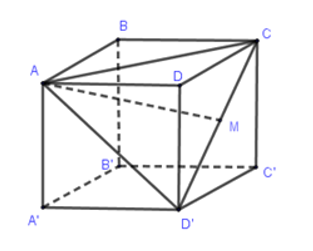
Gọi M là trung điểm của CD′.
Do ABCD.A′B′C′D′ là hình lập phương nên tam giác ACD′ là tam giác đều cạnh
AM⊥CD′⇒d(A,CD′)=AM=
Câu 7: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB' bằng
A.
B.
C.
D.
Đáp án: D
Giải thích:
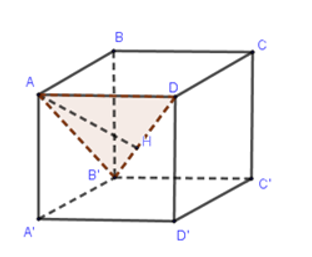
Gọi H là chân đường vuông góc hạ từ A xuống DB′.
Dễ thấy AD⊥(ABB′A′) nên
⇒ΔADB′ vuông đỉnh A.
Lại có AD=a;AB′=
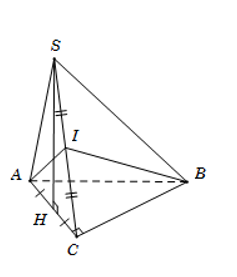
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I): AI⊥SC
(II): (SBC)⊥(SAC)
(III): AI⊥BC
(IV): (ABI)⊥(SBC)
A. 1
B. 2
C. 3
D. 4
Đáp án: D
Giải thích:
Tam giác SAC đều có I là trung điểm của SC nên AI⊥SC.
⇒ Mệnh đề (I) đúng.
Gọi H là trung điểm AC suy ra SH⊥AC.
Mà (SAC)⊥(ABC) theo giao tuyến AC nên SH⊥(ABC) do đó SH⊥BC.
Hơn nữa theo giả thiết tam giác ABC vuông tại C nên BC⊥AC.
Từ đó suy ra BC⊥(SAC)⇒BC⊥AI.. Do đó mệnh đề (III) đúng.
Từ mệnh đề (I) và (III) suy ra mệnh đề (IV) đúng.
Ta có: ⇒BC⊥(SAC)
BC⊂(SBC)⇒(SBC)⊥(SAC)
Vậy mệnh đề (II) đúng.
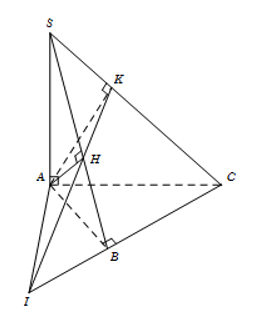
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Gọi H,K lần lượt là hình chiếu của A trên SB, SC và I là giao điểm của HK với mặt phẳng (ABC). Khẳng định nào sau đây sai?
A. BC⊥AH.
B. (AHK)⊥(SBC).
C. SC⊥AI.
D. Tam giác IAC đều
Đáp án: D
Giải thích:
Ta có ⇒BC⊥(SAB)
⇒BC⊥AH. Do đó A đúng.
Lại có AH⊥SB. Từ đó suy ra AH⊥(SBC)⇒AH⊥SC. (1)
Lại có theo giả thiết SC⊥AK. (2)
Từ (1) và (2), suy ra
SC⊥(AHK)⇒(SBC)⊥(AHK). Do đó B đúng.
Ta có ⇒SC⊥AI. Do đó C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
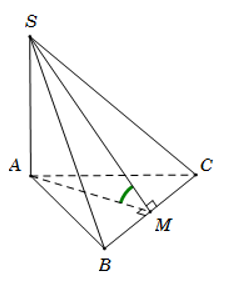
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = và vuông góc với mặt đáy (ABC). Gọi là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Đáp án: D
Giải thích:
Gọi M là trung điểm của BC, suy ra AM⊥BC
Ta có ⇒BC⊥(SAM)
⇒BC⊥SM
Tam giác ABC đều cạnh a, suy ra trung tuyến AM=
Tam giác vuông SAM có sin
Câu 11: Cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc và SA = SB = SC = 1. Tính cosα, trong đó α là góc giữa hai mặt phẳng (SBC) và (ABC) ?
A.
B.
C.
D.
Đáp án: D
Giải thích:
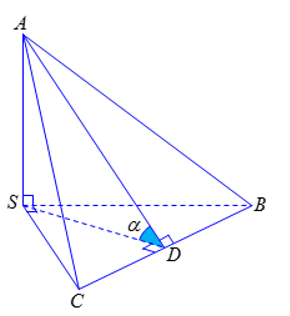
Gọi D là trung điểm cạnh BC.
Ta có ⇒ SA⊥(SBC)
⇒ SA⊥BC.
Mà SD⊥BC nên BC⊥(SAD).
Khi đó tam giác SAD vuông tại S có:
SD= và
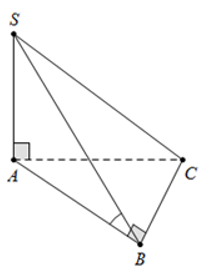
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a. Cạnh bên SA = a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng . Độ dài AC bằng
A.
B.
C. 2a
D. a
Đáp án: A
Giải thích:
Ta có (SBC)∩(ABC)=BC
Mặt khác SA⊥(ABC) và ΔABC vuông tại B⇒AB⊥BC.
Nên ⇒BC⊥(SAB)⇒BC⊥SB
Xét ΔSAB vuông tại A, có ⇒ SA=AB=a
Mà
Câu 13. Cho tam giác đều ABC cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại D lấy điểm S sao cho SD = . Gọi I là trung điểm BC; kẻ IH vuông góc SA (H thuộc SA). Khẳng định nào sau đây sai?
A. SA⊥BH
B. (SDB)⊥(SDC).
C. (SAB)⊥(SAC).
D. BH⊥HC.
Đáp án: B
Giải thích:
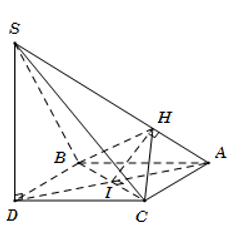
Từ giả thiết suy ra ABDC là hình thoi nên BC⊥AD.
Ta có ⇒BC⊥(SAD)
⇒BC⊥SA.
Lại có theo giả thiết IH⊥SA. Từ đó suy ra SA⊥(HCB)⇒SA⊥BH
⇒ Đáp án A đúng.
Tính được AI=
Ta có ΔAHI∼ΔADS⇒
⇒ Tam giác HBC có trung tuyến IH bằng nửa cạnh đáy BC nên hay BH⊥HC. Do đó D đúng.
Từ mệnh đề A và D suy ra BH⊥(SAC)⇒(SAB)⊥(SAC)⇒ mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Câu 14: Cho hình chóp S.ABC có cạnh SA⊥(ABC) và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây sai?
A. CH⊥HK
B. AB⊥(CHK)
C. CH⊥AK
D. BC⊥(SAC)
Đáp án: D
Giải thích:
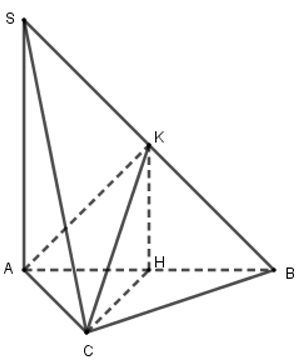
Do ΔABC cân tại C nên CH⊥AB.
Mà SA⊥(ABC) ⇒ SA⊥CH.
Do đó CH⊥(SAB) ⇒ CH⊥HK, CH⊥AK hay A, C đúng.
Ngoài ra HK//SA,SA⊥AB ⇒ HK⊥AB, mà AB⊥CH ⇒AB⊥(CHK) hay B đúng.
D sai vì BC không vuông góc với AC nên không có BC⊥(SAC).
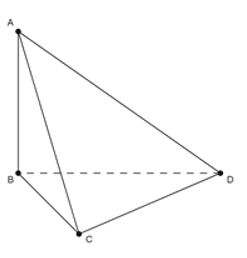
Câu 15: Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB.
B. Góc giữa AD và (ABC) là góc ADB.
C. Góc giữa AC và (ABD) là góc CAB.
D. Góc giữa CD và (ABD) là góc CBD.
Đáp án: A
Giải thích:
Từ giả thiết ta có ⇒AB⊥(BCD).
Do đó (AC,(BCD)=(AC,BC) =
Câu 16: Cho chóp đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 3. Gọi φ là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
A. tanφ=√7.
B. φ=
C. φ=
D. tanφ=
Đáp án: D
Giải thích:
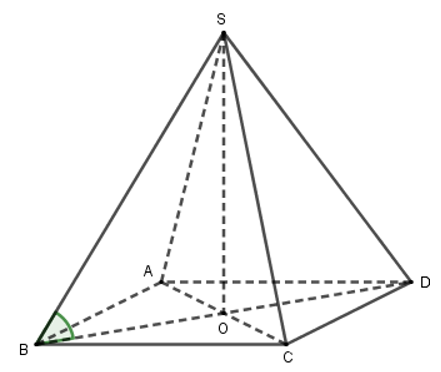
Gọi O là tâm mặt đáy (ABCD), suy ra SO⊥(ABCD).
Vì SO⊥(ABCD), suy ra OA là hình chiếu của SA trên mặt phẳng (ABCD).
Do đó
Tam giác vuông SOA, có tan=
Câu 17: Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Ba vectơ đồng phẳng là 3 vec tơ cùng nằm trong một mặt phẳng
B. Ba vectơ cùng phương khi và chỉ khi , với m,n là các số duy nhất
C. Ba vectơ đồng phẳng khi có với là vec tơ bất kỳ
D. Cả 3 mệnh đề trên đều sai
Đáp án: D
Giải thích:
Phương án A: sai vì chỉ cần giá của chúng song song hoặc nằm trên một mặt phẳng nào đó
Phương án B: sai vì ba véc tơ cùng phương ⇔
Phương án C sai vì điều kiện cần và đủ để ba véc tơ đồng phẳng là có các số m,n sao cho (với không cùng phương).
Câu 18: Cho ba vectơ không đồng phẳng xét các vectơ
;
Chọn mệnh đề đúng trong các mệnh đề sau:
A. Hai vec tơ cùng phương
B. Hai vec tơ cùng phương
C. Hai vec tơ cùng phương
D. Ba vec tơ không đồng phẳng
Đáp án: B
Giải thích:
Ta thấy nên cùng phương.
Do đó ba véc tơ đồng phẳng.
D sai.
Câu 19: Cho hình lập phương ABCD., Tìm giá trị của k thích hợp để
A. k=4
B. k=1
C. k=0
D. k=2
Đáp án: B
Giải thích:
Có
Câu 20: Cho hai điểm phân biệt A,B và một điểm O bất kì không thuộc đường thẳng AB. Mệnh đề nào sau đây là đúng?
A. Điểm M thuộc đường thẳng AB nếu và chỉ nếu
B. Điểm M thuộc đường thẳng AB nếu và chỉ nếu
C. Điểm M thuộc đường thẳng AB nếu và chỉ nếu
D. Điểm M thuộc đường thẳng AB nếu và chỉ nếu
Đáp án: C
Giải thích:
Điểm M thuộc đường thẳng AB nếu và chỉ nếu
Chứng minh:
Ta có: M∈AB⇔
Vậy C đúng.
Câu 21: Cho ABCD. là hình hộp, với K là trung điểm CC1. Tìm khẳng định đúng trong các khẳng định sau:
A.
B.
C.
D.
Đáp án: A
Giải thích:
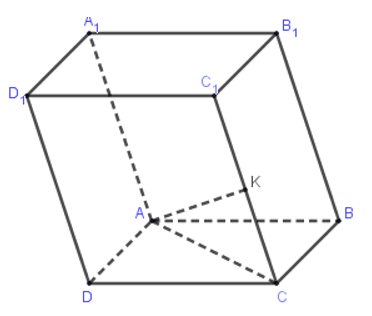
Có
Câu 22: Cho hình lăng trụ tam giác ABC.. Đặt ; trong các đẳng thức sau đẳng thức nào đúng.
A.
B.
C.
D.
Đáp án: C
Giải thích:
Ta có:
Câu 23: Cho hình hộp ABCD. với M= . Khi đó:
A.
B.
C.
D.
Đáp án: B
Giải thích:
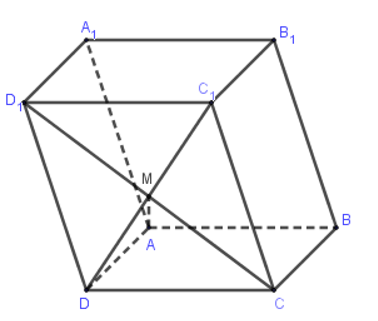
Ta có:
Câu 24: Trong các khẳng định sau đây, khẳng định nào sai?
A. Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng
B. Nếu ba vectơ có một vectơ thì ba vectơ đồng phẳng
C. Nếu giá của ba vectơ cùng song song với một mật phẳng thì ba vectơ đó đồng phẳng
D. Nếu trong ba vectơ có hai vectơ cùng phương thì ba vectơ đó đồng phẳng
Đáp án: A
Giải thích:
Ba véc tơ đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nên đáp án A sai.
Câu 25: Cho ba vectơ . Điều kiện nào dưới đây khẳng định ba vectơ đồng phẳng ?
A. Tồn tại ba số thực m,n,p thỏa mãn m+n+p=0 và
B. Tồn tại ba số thực m,n,p thỏa mãn m+n+p≠0 và
C. Tồn tại ba số thực m,n,p sao cho
D. Giá của đồng quy.
Đáp án: B
Giải thích:
Dựa vào đáp án, ta thấy rằng:
+) Với m + n + p = 0 ⇒ m = n = p = 0 suy ra nên chưa kết luận được ba vectơ đồng phẳng.
+) Với m + n + p ≠ 0 suy ra tồn tại ít nhất một số khác 0.
Giả sử m≠0, ta có
Suy ra tồn tại n, p để ba vectơ đồng phẳng.
Câu 26: Cho tứ diện ABCD có các cạnh đều bằng a. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau
A.
B.
C.
D.
Đáp án: D
Giải thích:
Phương án A:
nên A sai
Phương án B nên B sai
Phương án C:
nên C sai.
Phương án D: Do tứ diện ABCD đều nên AB⊥CD hay
Chú ý
Các em có thể dễ dàng chứng minh tứ diện đều ABCD có AB⊥CD bằng cách gọi M là trung điểm của CD và chứng minh CD⊥(ABM), từ đó chứng minh được các cặp cạnh đối còn lại cũng vuông góc.
Câu 27: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA⊥(ABCD). Biết SA= . Tính góc giữa SC và (ABCD).
A. 30∘
B. 45∘
C. 60∘
D. 75∘
Đáp án: A
Giải thích:
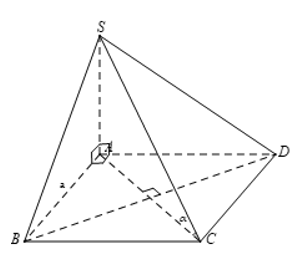
Ta có: SA⊥(ABCD)⇒SA⊥AC
⇒
ABCD là hình vuông cạnh a
⇒ AC=
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây là sai ?
A. SA⊥BD.
B. SC⊥BD.
C. SO⊥BD.
D. AD⊥SC.
Đáp án: D
Giải thích:
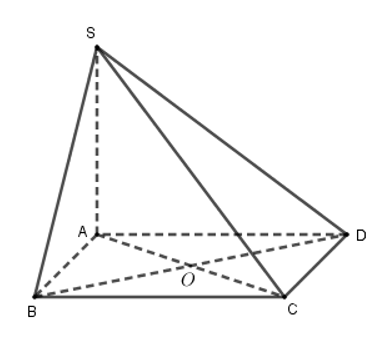
Vì SA vuông góc với mp(ABCD)⇒SA⊥BD.
Mà ABCD là hình thoi tâm O⇒AC⊥BD nên suy ra BD⊥(SAC).
Mặt khác SO⊂(SAC) và SC⊂(SAC)
suy ra
Và AD, SC là hai đường thẳng chéo nhau và .
Ta chưa kết luận được số đo của góc .
Câu 29: Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB=a, BC=b, CD=c. Độ dài đoạn thẳng AD bằng
A.
B.
C.
D.
Đáp án: A
Giải thích:
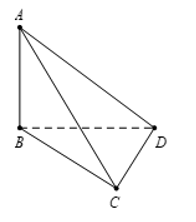
Ta có ⇒AB⊥(BCD)
⇒ tam giác ABD vuông tại B.
Lại có BC⊥CD nên tam giác BCD vuông tại C.
Khi đó:
Câu 30: Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau. Điểm nào dưới đây các đều bốn đỉnh A, B, C, D của tứ diện ABCD ?
A. Trung điểm của cạnh BD.
B. Tâm đường tròn ngoại tiếp tam giác ABC.
C. Trung điểm của cạnh AD.
D. Trọng tâm của tam giác ACD.
Đáp án: C
Giải thích:
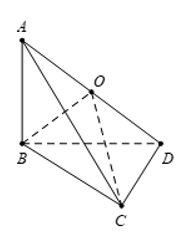
Ta có ⇒AB⊥(BCD)
⇒
Do đó; tam giác ABD vuông tại B.
Suy ra OA=OB=OD=, với O là trung điểm của AD. (1)
Lại có ⇒ CD⊥(ABC)
⇒tam giác ACD vuông tại C.
Suy ra OA=OC=OD= (2)
Từ (1),(2) suy ra OA= OB= OC= OD nên trung điểm O của cạnh AD cách đều A,B,C,D.
Câu 31: Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của đoạn thẳng AB
C. Mặt phẳng vuông góc với AB tại A
D. Đường thẳng qua A và vuông góc với AB
Đáp án: A
Giải thích:
Theo định nghĩa mặt phẳng trung trực
Câu 32: Cho a, b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
A. Nếu a ⊥ b và b ⊥ c thì a // c
B. Nếu a vuông góc với mặt phẳng (α) và b // (α) thì a ⊥ b
C. Nếu a // b và b ⊥ c thì c ⊥ a
D. Nếu a ⊥ b , b ⊥ c và a cắt c thì b vuông góc với mặt phẳng (a; c)
Đáp án: A
Giải thích:
Nếu 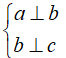
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).
A. 30°
B. 45°
C. 60°
D. 75°
Đáp án: C
Giải thích:
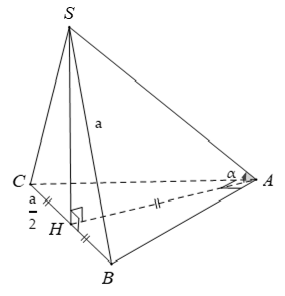
Gọi H là trung điểm của BC suy ra
AH = BH = CH = (1/2)BC = a/2
Câu 34: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 60°
B.90°
C. 45°
D. 30°
Đáp án: C
Giải thích:
Do H là hình chiếu của S lên mặt phẳng ( ABC) nên SH ⊥ (ABC)
Vậy AH là hình chiếu của SH lên mp(ABC)
⇒ (SA, (ABC)) = (SA, AH) = ∠ SAH
Ta có: SH ⊥ (ABC) ⇒ SH ⊥ AH
Mà: ΔABC = ΔSBC ⇒ SH = AH
Vậy tam giác SAH vuông cân tại H ⇒ SAH = 45°
Chọn C
Câu 35: Cho hình chóp S. ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:
A. 45°
B. 120°
C. 90°
D. 65°
Đáp án: C
Giải thích:
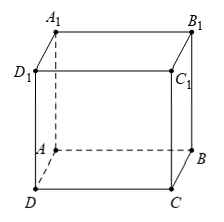
Câu 36: Cho hình hộp ABDC.A1B1C1D1. Khẳng định nào dưới đây là sai ?
Đáp án: D
Giải thích:
Dựa vào đáp án, ta thấy rằng:
Câu 37: Cho tứ diện ABCD và I là trọng tâm tam giác ABC. Đẳng thức đúng là.
Đáp án: D
Giải thích:
Vì I là trọng tâm tam giác ABC nên:
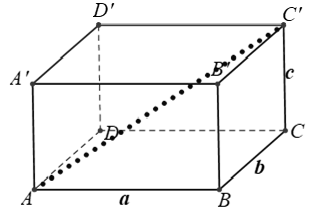
Câu 38: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Độ dài đường chéo AC' là
Đáp án: A
Giải thích:
Áp dụng định lí Py-ta-go vào tam giác vuông ABB’ ta có :
Do ABCD.A’B’C’D’ là hình lập phương nên:
B’C’ ⊥ (ABB'A') ⇒ B'C ⊥ AB'
Áp dụng định lí Py-ta-go vào tam giác vuông AB’C’ ta có:
Vậy đường chéo hình hộp chữ nhật
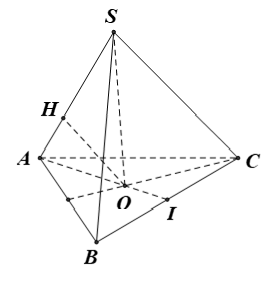
Câu 39: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SO = a√3/3. Khoảng cách từ điểm O đến cạnh bên SA bằng
Đáp án: B
Giải thích:
Chọn B
Vì hình chóp S.ABC đều có SO là đường cao
⇒ O là tâm của tam giác ABC.
+ Gọi I là trung điểm cạnh BC.
Tam giác ABC đều nên
Kẻ OH ⊥ SA; khi đó d(O; SA) = OH
Xét tam giác SAO vuông tại O:
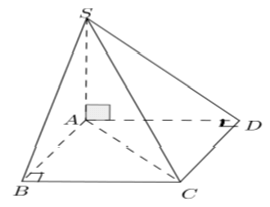
Câu 40: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách giữa SD và BC.
Đáp án: D
Giải thích:
Ta có: BC // AD (Tính chất hình chữ nhật) mà AD ⊂ (SAD)
⇒ BC // mp(SAD)
d(BC, SD) = d(BC, (SAD)) = d(B, SAD)
Vậy d(SD; BC) = AB = a√3
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Vectơ trong không gian có đáp án
Trắc nghiệm Hai đường thẳng vuông góc có đáp án
Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án