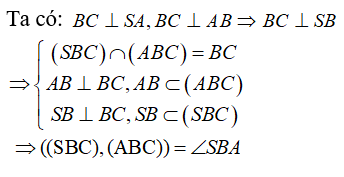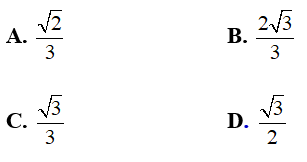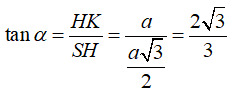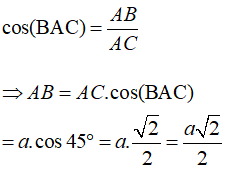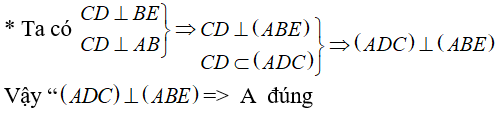TOP 40 câu Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 4: Hai mặt phẳng vuông góc có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 4.
Trắc nghiệm Toán 11 Bài 4: Hai mặt phẳng vuông góc
Câu 1: Cho hình chóp S.ABCD, đáy ABCD là hình vuông, . Gọi là mặt phẳng chứa AB và vuông góc với , cắt chóp S.ABCD theo thiết diện là hình gì?
A. hình bình hành.
B. hình thang vuông.
C. hình thang không vuông.
D. hình chữ nhật.
Đáp án: B
Giải thích:
Dựng
Ta có .
Suy ra
mà suy ra
Do đó
Vì nên
.
Từ đó thiết diện là hình thang ABKH.
Mặt khác nên
Vậy thiết diện là hình thang vuông tại A và H.
Câu 2: Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có vuông góc với đáy và . Gọi là mặt phẳng qua SO và vuông góc với Diện tích thiết diện của và hình chóp S.ABCD bằng bao nhiêu?
A.
B.
C.
D.
Đáp án: B
Giải thích:
Gọi MN là đoạn thẳng qua O vuông góc AD ( M,N thuộc AD,BC ) ta có
nên SMN là thiết diện cần tìm.
vuông tại M nên
Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Đáp án: C
Câu 4: Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Cho hai đường thẳng a và b vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì song song với đường kia.
B. Cho đường thẳng , mọi mặt phẳng chứa a thì .
C. Cho hai đường thẳng chéo nhau a và b, luôn luôn có mặt phẳng chứa đường này và vuông góc với đường thẳng kia.
D. Cho hai đường thẳng a và b vuông góc với nhau, nếu mặt phẳng chứa a và mặt phẳng chứa b thì .
Đáp án: B
Câu 5: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng?
A. Có ba cặp mặt phẳng vuông góc với nhau.
B. Có hai cặp mặt phẳng vuông góc với nhau.
C. Có năm cặp mặt phẳng vuông góc với nhau.
D. Có bốn cặp mặt phẳng vuông góc với nhau.
Đáp án: C
Câu 6: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
B. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Một mặt phẳng và một đường thẳng a không thuộc cùng vuông góc với đường thẳng b thì .
Đáp án: D
Câu 7: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Đáp án: D
Câu 6: Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng.
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
B. Nếu hai mặt vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng và vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc và mỗi điểm B thuộc thì ta có đường thẳng vuông góc với.
D. Nếu hai mặt phẳng và đều vuông góc với mặt phẳng thì giao tuyến của và nếu có sẽ vuông góc với .
Đáp án: D
Giải thích:
Theo Định lí .
Câu 8: Cho hai mặt phẳng và vuông góc với nhau và gọi .
I. Nếu và thì .
II. Nếu thì .
III. Nếu b d thì b hoặc b ().
IV. Nếu thì và
Các mệnh đề đúng là:
A. I, II và III.
B. III và IV.
C. II và III.
D. I, II và IV.
Đáp án: D
Câu 9: Cho hai mặt phẳng và cắt nhau và một điểm M không thuộc và . Qua M có bao nhiêu mặt phẳng vuông góc với và ?
A. 1.
B. 2.
C. 3.
D. Vô số.
Đáp án: A
Câu 10: Cho hai mặt phẳng và , a là một đường thẳng nằm trên . Mệnh đề nào sau đây sai ?
A. Nếu với thì .
B. Nếu thì
C. Nếu a cắt thì cắt
D. Nếu thì .
Đáp án: B
Giải thích:
Gọi nếu thì .
Câu 11: Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Cho hai đường thẳng chéo nhau a và b đồng thời . Luôn có mặt phẳng chứa a và .
C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng chứa a và mặt phẳng chứa b thì .
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
Đáp án: B
Câu 12: Cho hai mặt phẳng và song song với nhau và một điểm M không thuộc và . Qua M có bao nhiêu mặt phẳng vuông góc với và ?
A. 2
B. 3
C. 1
D. Vô số.
Đáp án: D
Giải thích:
Qua M dựng đường thẳng vuông cóc với và . Khi đó có vô số mặt phẳng xoay quanh thỏa yêu cầu bài toán.
Câu 13: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Cả ba mệnh đề trên đều sai.
Đáp án: D
Câu 14: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một mặt phẳng và một đường thẳng a không thuộc cùng vuông góc với đường thẳng thì song song với a
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
Đáp án: A
Giải thích:
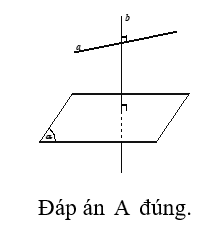
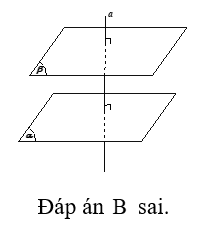
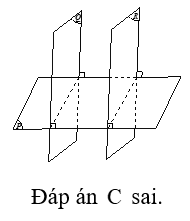
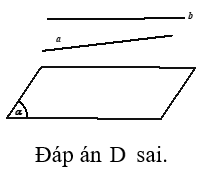
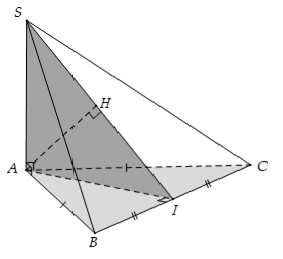
Câu 15: Cho hai mặt phẳng vuông góc và có giao tuyến . Lấy A,B cùng thuộc và lấy C trên , D trên sao cho , và . Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng đi qua A và vuông góc với CD là?
A.
B.
C.
D.
Đáp án: C
Giải thích:
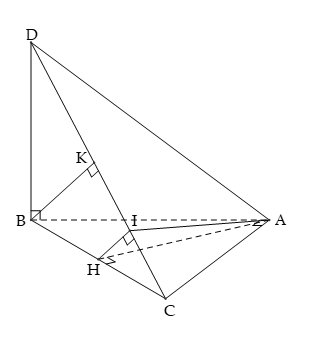
Ta có:
Gọi H là trung điểm BC, ta có
Trong mặt phẳng , kẻ thì ta có
Khi đó mặt phẳng cắt tứ diện ABCD theo thiết diện là tam giác AHI
Mặt khác tam giác ABC vuông cân tại A nên .
Trong tam giác vuông BCD, kẻ đường cao BK thì và
Vậy: thiết diện cần tìm là tam giác AHI vuông tại H và có diện tích
Câu 16: Cho hình chóp cụt đều với đáy lớn ABC có cạnh bằng a. Đáy nhỏ có cạnh bằng , chiều cao . Khẳng định nào sau đây sai?
A. Ba đường cao , , đồng qui tại.
B.
C. Góc giữa mặt bên mặt đáy là góc SIO ( I là trung điểm BC).
D. Đáy lớn ABC có diện tích gấp 4 lần diện tích đáy nhỏ .
Đáp án: B
Giải thích:
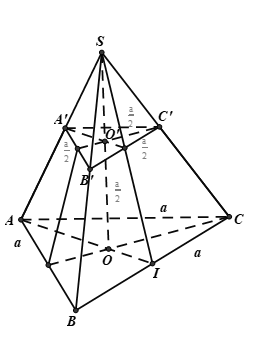
+ Đáp án A đúng.
+ Gọi I là trung điểm của BC.
Từ giả thiết dễ dàng chỉ ra được
. Mặt khác là tam giác đều cạnh a, có AI là đường trung tuyến
Áp dụng định lý Pytago trong vuông tại O ta có:
Vì là hình chóp cụt đều nên
đáp án B sai.
+ Ta có: .
Vì cân tại S và I là trung điểm của BC nên suy ra .
Mặt khác là tam giác đều có I là trung điểm của BC
đáp án C đúng.
+ Ta có:
đáp án D đúng.
Câu 17: Cho hình chóp cụt tứ giác đều cạnh của đáy nhỏ ABCD bằng và cạnh của đáy lớn bằng a. Góc giữa cạnh bên và mặt đáy bằng . Tính chiều cao của hình chóp cụt đã cho.
A.
B.
C.
D.
Đáp án: A
Giải thích:
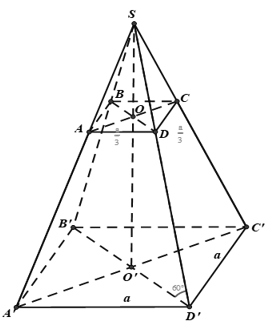
Ta có
là hình chiếu vuông góc của lên .
Từ giả thiết dễ dàng chỉ ra được
Vì là tam giác vuông cân tại có là đường cao nên ta có:
Áp dụng hệ thức lượng trong vuông tại ta có:
Câu 18: Cho hình lăng trụ lục giác đều có cạnh bên bằng a và là hình vuông. Cạnh đáy của lăng trụ bằng:
A. a
B.
C.
D.
Đáp án: B
Giải thích:
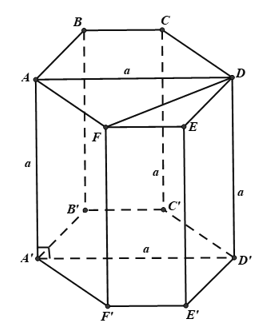
Tổng số đo các góc của hình lục giác là . Vì là hình lục giác đều nên mỗi góc của hình lục giác đều là
. Vì là hình lục giác đều nên ta suy ra:
+ AD là tia phân giác của góc và
+ Tam giác AFD vuông tại F.
Xét tam giác AFD vuông tại F có và ta suy ra:
Câu 19: Cho hình lăng trụ tứ giác đều có là hình vuông, cạnh bằng a . Cạnh đáy của hình lăng trụ bằng:
A.
B.
C.
D.
Đáp án: A
Giải thích:
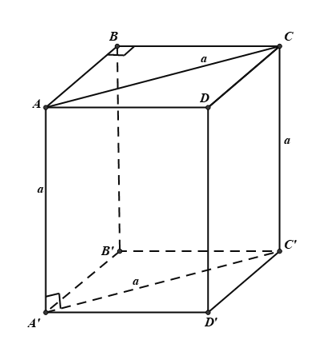
Từ giả thiết ta suy ra vuông cân tại B
Áp dụng hệ thức lượng trong vuông cân tại B có và cạnh , ta có:
Câu 20: Cho hình lăng trụ tam giác đều có cạnh đáy bằng và cạnh bên bằng 2a. Gọi G và lần lượt là trọng tâm của hai đáy ABC và . Khẳng định nào sau đây đúng khi nói về ?
A. là hình chữ nhật có hai kích thước là 2a và 3a.
B. là hình vuông có cạnh bằng 2a.
C. là hình chữ nhật có diện tích bằng .
D. là hình vuông có diện tích bằng
Đáp án: B
Giải thích:
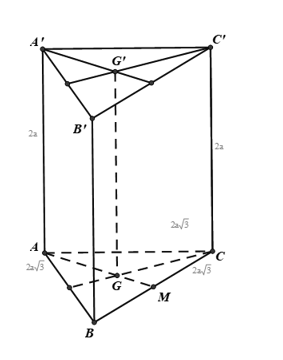
Gọi M là trung điểm BC. Khi đó ta dễ dàng tính được:
Vì G là trọng tâm tam giác ABC nên:
là hình vuông có cạnh bằng 2a.
Câu 22: Cho tứ diện ABCD có hai mặt phẳng và cùng vuông góc với . Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A.
B.
C.
D.
Đáp án: B
Giải thích:
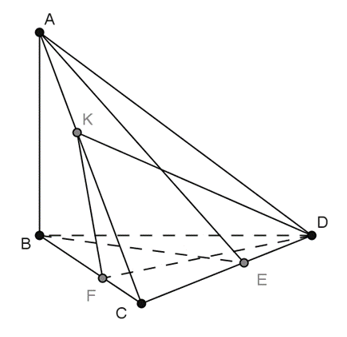
Ta có:
Mặt khác:
nên câu A đúng.
nên câu C đúng.
Theo trên ta có nên .
Vậy ta có
.
Do đó câu D đúng.
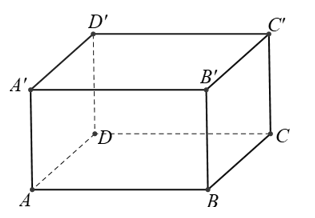
Câu 23: Cho hình hộp chữ nhật . Khẳng định nào sau đây không đúng?
A. Tồn tại điểm O cách đều tám đỉnh của hình hộp.
B. Hình hộp có 6 mặt là 6 hình chữ nhật.
C. Hai mặt và vuông góc nhau.
D. Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.
Đáp án: C
Giải thích:
Câu 24: Cho hình chóp có hai mặt bên và vuông góc với đáy . Khẳng định nào sau đây sai ?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Đáp án: D
Giải thích:
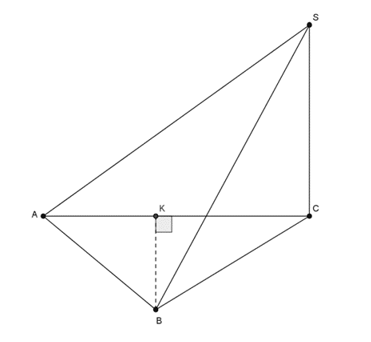
Ta có:
. Do đó câu A và B đúng
C. Sai. vì nếu thì hai mặt phẳng và phải vuông góc với nhau theo giao tuyến SB
D. Ta có:
theo giao tuyến AC
Mà BK là đường cao của .
Vậy D đúng
Câu 25: Cho hình lăng trụ . Hình chiếu vuông góc của lên trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?
A. là hình chữ nhật.
B.
C.
D.
Đáp án: D
Giải thích:
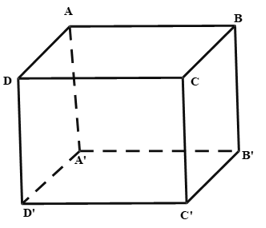
Ta có nên ,
nếu thì vô lý vì H trùng A
Câu 26: Cho hình chóp có và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên . Khẳng định nào sau đây đúng?
A.
B. H trùng với trọng tâm tam giác SBC.
C.
D. (I là trung điểm của BC).
Đáp án: D
Giải thích:
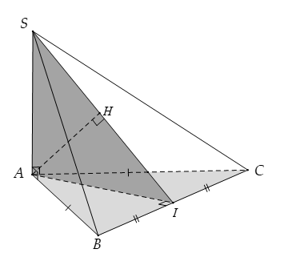
Gọi I là trung điểm của BC
mà
Khi đó H là hình chiếu vuông góc của A lên .
Suy ra .
Câu 27: Cho hình chóp có hai mặt bên và vuông góc với đáy . Khẳng định nào sau đây sai?
A.
B. Nếu là hình chiếu vuông góc của A lên thì .
C. .
D. BK là đường cao của tam giác ABC thì .
Đáp án: B
Giải thích:
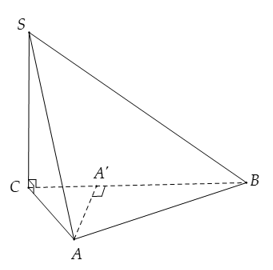
Ta có:
Gọi là hình chiếu vuông góc của A lên ,
khi đó
Suy ra đáp án B sai
Câu 28: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Đáp án: C
Giải thích: Đường thẳng thỏa mãn cần tìm là đường thẳng đi qua điểm A cho trước và vuông góc với mặt phẳng (P) cho trước. Đây là đường thẳng cố định.
Câu 29: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng?
A. Có ba cặp mặt phẳng vuông góc với nhau
B. Có hai cặp mặt phẳng vuông góc với nhau
C. Có năm cặp mặt phẳng vuông góc với nhau
D. Có bốn cặp mặt phẳng vuông góc với nhau
Đáp án: C
Giải thích:
Xét hình chóp S.ABCD có đáy là hình vuông và SA ⊥ (ABCD)
+ Do SA ⊂ (SAB) và SA ⊥ (ABCD) nên (SAB) ⊥ (ABCD)
+ Do SA ⊂ (SAD) và SA ⊥ (ABCD) nên (SAD) ⊥ (ABCD)
+ Do AD ⊥ SA, AD ⊥ AB nên AD ⊥ ( SAB)
AD ⊂ (SAD) và AD ⊥ (SAB) nên (SAD) ⊥ (SAB).
+ Chứng minh tương tự; ta có: (SAD) ⊥ (SCD) và (SAB) ⊥ (SBC).
⇒ có tất cả năm cặp mặt phẳng vuông góc với nhau.
Câu 30: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Đáp án: B
Giải thích:
Chọn đáp án B
A sai vì đáy có thể là hình bình hành.
B đúng
C sai vì đáy có thể là hình bình hành
D sai vì đáy có thể là hình bình hành.
Câu 31: Mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Đáp án: D
Giải thích:
Mệnh đề A sai vì có thể xảy ra trường hợp hai mặt phẳng vuông góc với nhau nhưng đường thẳng thuộc mặt phẳng này song song với mặt phẳng kia.
Mệnh đề B sai vì xảy ra trường hợp hai mặt phẳng song song.
Mệnh đề C sai vì xảy ra trường hợp hai mặt phẳng vuông góc.
Chọn đáp án D
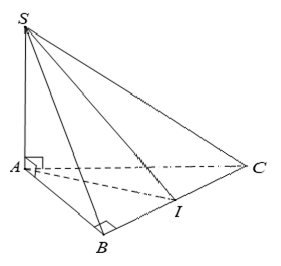
Câu 32: Cho hình chóp S.ABC có hai mặt bên (SAB) và(SAC) vuông góc với mặt phẳng (ABC) , tam giác ABC vuông cân ở A và có đường cao AH (H ∈ BC) . Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây sai ?
A. SA ⊥ (ABC)
B. O ∈ SH
C. (SAH) ⊥ (SBC)
D. ((SBC), (ABC)) = ∠SBA
Đáp án: D
Giải thích:
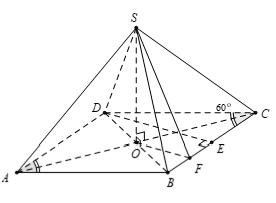
Câu 33: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF)và (SBC) là
A. 90°
B. 60°
C. 30°
D. 45°
Đáp án: A
Giải thích:
Tam giác BCD có BC = BD và ∠BCD = 60° nên tam giác BCD đều
Lại có E là trung điểm BC ⇒ DE ⊥ BC
Mặt khác, tam giác BDE có OF là đường trung bình
⇒ OF // DE ⇒ BC ⊥ OF (1).
+ Do SO ⊥ (ABCD) ⇒ BC ⊥ SO (2).
+ Từ (1) và (2), suy ra BC ⊥ (SOF) ⇒ (SBC) ⊥ (sOF)
Vậy, góc giữa ( SOF) và( SBC) bằng 90°
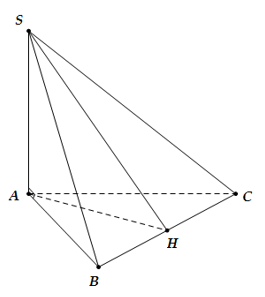
Câu 34: Cho hình chóp S. ABC có SA ⊥ (ABC) và AB ⊥ BC , gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
A. Góc SBA.
B. Góc SCA.
C. Góc SCB.
D. Góc SIA.
Đáp án: A
Giải thích:
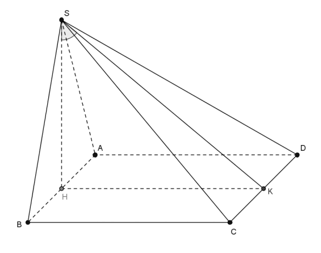
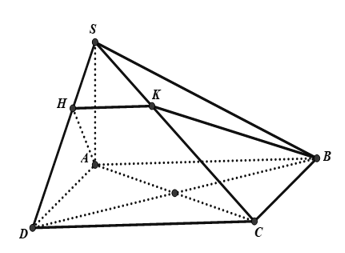
Câu 35: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H; K lần lượt là trung điểm của AB, CD. Ta có tan của góc tạo bởi hai mặt phẳng (SAB) và (SCD) bằng :
Đáp án: B
Giải thích:
Ta có:
Vì H là trung điểm của AB
⇒ SH ⊥ AB ⇒ SH ⊥ d (vì d // AB)
⇒ d ⊥ SK (theo định lý ba đường vuông góc)
Do đó: ∠KSH = α là góc giữa (SAB) và (SCD)
Mà SH là đường cao trong tam giác SAB đều cạnh a ⇒ SH = a√3/2
Xét tam giác SHK vuông tại H có:
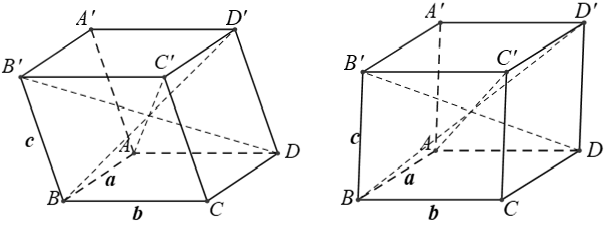
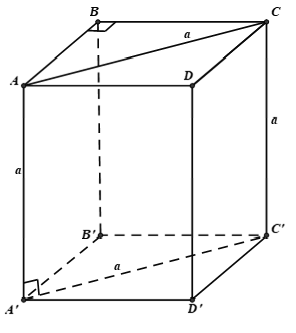
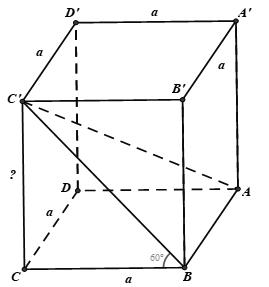
Câu 36: Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC’ = c. Nếu AC' = BD' = B'D = √(a2 + b2 + c2) thì hình hộp là
A. Hình lập phương
B. Hình hộp chữ nhật
C. Hình hộp thoi
D. Hình hộp đứng
Đáp án: B
Giải thích:
Nếu AC’= BD’ ⇒ hình bình hành ABC’D’ là hình chữ nhật
Nếu BD’= B’D ⇒ hình bình hành BDD’B’ là hình chữ nhật
Nếu AC’= B’D ⇒ hình bình hành ADC’B’ là hình chữ nhật
⇒ nếu AC’ = BD’ = B’D thì hình hộp là hình hộp chữ nhật.
Chọn B
Câu 37: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC’A’ là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:
Đáp án: A
Giải thích:
+ Do ABCD. A’B’C’D’ là hình lăng trụ tứ giác đều nên tam giác ABC vuông cân tại B. ⇒ ∠BAC = ∠BCA = 45°
+ Áp dụng hệ thức lượng trong tam giác ABC vuông cân tại B có ∠BAC = 45° và cạnh AC = a, ta có:
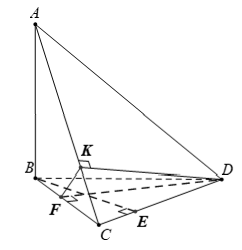
Câu 38: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?
A. (ADC) ⊥ (ABE)
B. (ADC) ⊥ (DFK)
C. (ADC) ⊥ (ABC)
D. (BDC) ⊥ (ABE)
Đáp án: C
Giải thích:
Ta xét các phương án:
Câu 39: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
A. H ∈ SB
B. H trùng với trọng tâm tam giác SBC.
C. H ∈ SC
D. H ∈ SI (I là trung điểm của BC).
Đáp án: D
Giải thích:
Gọi I là trung điểm của BC
⇒ AI ⊥ BC mà BC ⊥ SA ⇒ BC ⊥ (SAI)
⇒ SI ⊥ BC (1)
Khi đó H là hình chiếu vuông góc của A lên (SBC) .
Suy ra AH ⊥ BC
Lại có: SA ⊥ BC
⇒ BC ⊥ (SAH) ⇒ BC ⊥ SH (2)
Từ (1) và (2) suy ra 3 điểm S; H; I thẳng hàng.
Câu 40: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC’) có số đo bằng 60°. Cạnh bên của hình lăng trụ bằng:
A. 3a
B. a√3
C. 2a
D. a√2
Đáp án: A
Giải thích:
Chọn B.
Ta có: (ABCD) ∩ (ABC') = AB
Ta có: AB ⊥ BC và AB ⊥ BB' (vì lăng trụ đã cho là lăng trụ tứ giác đều)
⇒ AB ⊥ (BB'C'C) mà C'B ⊂ (BB'C'C) ⇒ AB ⊥ C'B
Mặt khác: CB ⊥ AB
⇒ ((ABCD), (ABC')) = (CB, C'B) = ∠ CBC' = 60°
Áp dụng hệ thức lượng trong tam giác BCC’ vuông tại C ta có:
tan(CBC') = CC'/CB ⇒ CC' = CB.tan(CBC') = a.tan60° = a√3
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Vectơ trong không gian có đáp án
Trắc nghiệm Hai đường thẳng vuông góc có đáp án
Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án