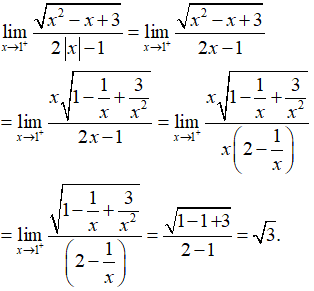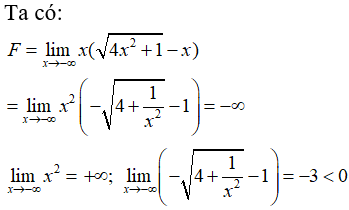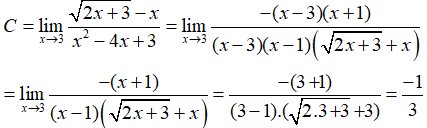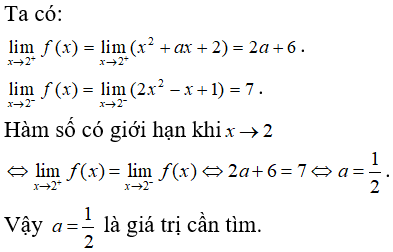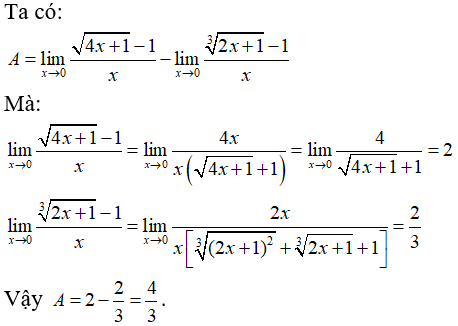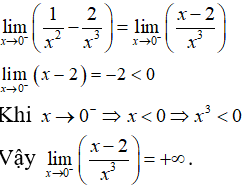TOP 40 câu Trắc nghiệm Giới hạn của hàm số (có đáp án 2023) – Toán 11

Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 2: Giới hạn của hàm số có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 2.

1 1,347 12/01/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 11 Bài 2: Giới hạn của hàm số

Bài giảng Trắc nghiệm Toán 11 Bài 2: Giới hạn của hàm số

Câu 1: Giá trị của giới hạn $\lim_{x \to 3} \sqrt{\frac{9 x^{2} - x}{(2 x - 1) (x^{4} - 3)}}$ là:

A. $\frac{1}{5}$

B. $\sqrt{5}$

C. $\frac{1}{\sqrt{5}}$

D. 5.

Hiển thị đáp án

Đáp án: C

Giải thích:

$\begin{array}{l} \lim_{x \to 3} \sqrt{\frac{9 x^{2} - x}{(2 x - 1) (x^{4} - 3)}} \\ = \sqrt{\frac{{9.3}^{2} - 3}{(2.3 - 1) (3^{4} - 3)}} \end{array}$

$= \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$

Câu 2: Giá trị của giới hạn $\lim_{x \to - \infty} ({|x|}^{3} + 2 x^{2} + 3 |x|)$ là:

A. 0.

B. +∞.

C. 1.

D. −∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $x < 0$ nên:

$\begin{array}{l} \lim_{x \to - \infty} ({|x|}^{3} + 2 x^{2} + 3 |x|) \\ = \lim_{x \to - \infty} (- x^{3} + 2 x^{2} - 3 x) \\ = \lim_{x \to - \infty} x^{3} . (- 1 + \frac{2}{x} - \frac{3}{x^{2}}) \\ = + \infty \end{array}$

Vì $\begin{array}{l} \lim_{x \to - \infty} x^{3} = - \infty, \\ \lim_{x \to - \infty} (- 1 + \frac{2}{x} - \frac{3}{x^{2}}) = - 1 < 0 \end{array}$

Câu 3: Tính $\lim_{x \to + \infty} (\sqrt{x^{2} + x + 3} - x)$ bằng?

A. −1

B. 0

C. $\frac{1}{2}$

D. 1

Hiển thị đáp án

Đáp án: C

Giải thích:

$\begin{array}{l} \lim_{x \to + \infty} (\sqrt{x^{2} + x + 3} - x) \\ = \lim_{x \to + \infty} \frac{x^{2} + x + 3 - x^{2}}{\sqrt{x^{2} + x + 3} + x} \\ = \lim_{x \to + \infty} \frac{x + 3}{\sqrt{x^{2} + x + 3} + x} \\ = \lim_{x \to + \infty} \frac{1 + \frac{3}{x}}{\sqrt{1 + \frac{1}{x} + \frac{3}{x^{2}}} + 1} \\ = \frac{1 + 0}{\sqrt{1 + 0 + 0} + 1} = \frac{1}{2} \end{array}$

Câu 4: Tính $\lim_{x \to - \infty} (\sqrt[3]{x^{3} + 1} + x - 1)$ bằng?

A. −1

B. 0

C. $\frac{1}{2}$

D. −∞

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to - \infty} (\sqrt[3]{x^{3} + 1} + x - 1) \\ = \lim_{x \to - \infty} (x \sqrt[3]{1 + \frac{1}{x^{3}}} + x - 1) \\ = \lim_{x \to - \infty} [x (\sqrt[3]{1 + \frac{1}{x^{3}}} + 1 - \frac{1}{x})] \\ = - \infty \end{array}$

Vì $\lim_{x \to - \infty} x = - \infty;$

$\lim_{x \to - \infty} (\sqrt[3]{1 + \frac{1}{x^{3}}} + 1 - \frac{1}{x}) = 2 > 0$

Câu 5: Kết quả của giới hạn $\lim_{x \to {(- 1)}^{+}} (x^{3} + 1) \sqrt{\frac{x}{x^{2} - 1}}$ là:

A. 3.

B. +∞.

C. 0.

D. −∞

Hiển thị đáp án

Đáp án: C

Giải thích:

Với $x \in (- 1; 0)$ thì $x + 1 > 0$ và $\frac{x}{x - 1} > 0$

Do đó

$\begin{array}{l} \lim_{x \to {(- 1)}^{+}} (x^{3} + 1) \sqrt{\frac{x}{x^{2} - 1}} \\ = \lim_{x \to {(- 1)}^{+}} (x + 1) (x^{2} - x + 1) \sqrt{\frac{x}{(x - 1) (x + 1)}} \\ = \lim_{x \to {(- 1)}^{+}} \sqrt{x + 1} (x^{2} - x + 1) \sqrt{\frac{x}{x - 1}} \\ = \sqrt{- 1 + 1} . [- (- 1) + 1] . \sqrt{\frac{- 1}{- 1 - 1}} = 0 \end{array}$

Câu 6: Giá trị của giới hạn $\lim_{x \to 2} \sqrt[3]{\frac{x^{2} - x - 1}{x^{2} + 2 x}}$ là:

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{1}{3}$

D. $\frac{1}{5}$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\begin{array}{l} \lim_{x \to 2} \sqrt[3]{\frac{x^{2} - x - 1}{x^{2} + 2 x}} \\ = \sqrt[3]{\frac{2^{2} - 2 - 1}{2^{2} + 2.2}} \\ = \sqrt[3]{\frac{1}{8}} = \frac{1}{2} \end{array}$

Câu 7: Giá trị của giới hạn $\lim_{x \to \sqrt{3}} |x^{2} - 4|$ là:

A. 0.

B. 1.

C. 2.

D. 3.

Hiển thị đáp án

Đáp án: B

Giải thích:

$\begin{array}{l} \lim_{x \to \sqrt{3}} |x^{2} - 4| = |{(\sqrt{3})}^{2} - 4| \\ = |- 1| = 1 \end{array}$

Câu 8: Giá trị của giới hạn $\lim_{x \to - \infty} (x - x^{3} + 1)$ là:

A. 1.

B. −∞.

C. 0.

D. +∞.

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to - \infty} (x - x^{3} + 1) \\ = \lim_{x \to - \infty} x^{3} (\frac{1}{x^{2}} - 1 + \frac{1}{x^{3}}) \\ = + \infty \end{array}$

vì $\{\begin{cases} \lim_{x \to - \infty} x^{3} = - \infty \\ \underset{x \to - \infty}{\lim (\frac{1}{x^{2}} - 1 + \frac{1}{x^{3}})} = - 1 < 0 \end{cases}$

Câu 9: Kết quả của giới hạn $\lim_{x \to 2^{+}} \frac{x - 15}{x - 2}$ là:

A. −∞

B. +∞

C. $- \frac{15}{2}$

D. 1

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì $\begin{array}{l} \{\begin{cases} \lim_{x \to 2^{+}} (x - 15) = 2 - 15 = - 13 < 0 \\ \lim_{x \to 2^{+}} (x - 2) = 2 - 2 = 0 \\ x - 2 > 0, \forall x > 2 \end{cases} \\ \Rightarrow \lim_{x \to 2^{+}} \frac{x - 15}{x - 2} = - \infty \end{array}$

Câu 10: Kết quả của giới hạn $\lim_{x \to 2^{+}} \frac{\sqrt{x + 2}}{\sqrt{x - 2}}$ là:

A. −∞.

B. +∞.

C. −152.

D. Không xác định.

Hiển thị đáp án

Đáp án: B

Giải thích:

Vì

$\{\begin{cases} \lim_{x \to 2^{+}} \sqrt{x + 2} = \sqrt{2 + 2} = 2 > 0 \\ \lim_{x \to 2^{+}} \sqrt{x - 2} = \sqrt{2 - 2} = 0 \\ \sqrt{x - 2} > 0, \forall x > 2 \end{cases}$

$\Rightarrow \lim_{x \to 2^{+}} \frac{\sqrt{x + 2}}{\sqrt{x - 2}} = + \infty$

Câu 11: Chọn mệnh đề đúng:

A. $\lim_{x \to + \infty} f (x) = + \infty \Leftrightarrow \lim_{x \to + \infty} [- f (x)] = + \infty$

B. $\lim_{x \to + \infty} f (x) = + \infty \Leftrightarrow \lim_{x \to + \infty} [- f (x)] = - \infty$

C. $\lim_{x \to + \infty} f (x) = + \infty \Leftrightarrow \lim_{x \to - \infty} [- f (x)] = - \infty$

D. $\lim_{x \to + \infty} f (x) = - \infty \Leftrightarrow \lim_{x \to + \infty} [- f (x)] = - \infty$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\lim_{x \to + \infty} f (x) = + \infty$

$\Leftrightarrow \lim_{x \to + \infty} [- f (x)] = - \infty$

Câu 12: Giá trị của giới hạn $\lim_{x \to + \infty} (\sqrt{x^{2} + 1} + x)$ là:

A. 0.

B. +∞.

C. $\sqrt{2} - 1$ .

D. −∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

$\lim_{x \to + \infty} (\sqrt{x^{2} + 1} + x)$

$= \lim_{x \to + \infty} x (\sqrt{1 + \frac{1}{x^{2}}} + 1)$

$= + \infty$

vì $\{\begin{cases} \lim_{x \to + \infty} x = + \infty \\ \lim_{x \to + \infty} (\sqrt{1 + \frac{1}{x^{2}}} + 1) = 2 > 0 \end{cases}$

Câu 13: Giá trị của giới hạn $\lim_{x \to + \infty} (\sqrt[3]{3 x^{3} - 1} + \sqrt{x^{2} + 2})$ là:

A. $\sqrt[3]{3} + 1$

B. +∞.

C. $\sqrt[3]{3} - 1$

D. −∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

$\lim_{x \to + \infty} (\sqrt[3]{3 x^{3} - 1} + \sqrt{x^{2} + 2})$

$= \lim_{x \to + \infty} x (\sqrt[3]{3 - \frac{1}{x^{3}}} + \sqrt{1 + \frac{2}{x^{2}}})$

$= + \infty$

Vì

$\{\begin{cases} \lim_{x \to + \infty} x = + \infty \\ \lim_{x \to + \infty} (\sqrt[3]{3 - \frac{1}{x^{3}}} + \sqrt{1 + \frac{2}{x^{2}}}) \\ = \sqrt[3]{3} + 1 > 0 \end{cases}$

Câu 14: Cho hàm số $f (x) = \{\begin{cases} \frac{2 x}{\sqrt{1 - x}}, x < 1 \\ \sqrt{3 x^{2} + 1}, x \geq 1 \end{cases}$ .

Khi đó $\lim_{x \to 1^{+}} f (x)$ là:

A. +∞.

B. 2.

C. 4.

D. −∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

$\lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{+}} \sqrt{3 x^{2} + 1}$

$= \sqrt{{3.1}^{2} + 1} = 2$

Câu 15: Giá trị của giới hạn $\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$ là:

A. 1

B. −2

C. 0

D. −32.

Hiển thị đáp án

Đáp án: C

Giải thích:

$\lim_{x \to 1} \frac{x - x^{3}}{(2 x - 1) (x^{4} - 3)}$

$= \frac{1 - 1^{3}}{(2.1 - 1) (1^{4} - 3)} = 0$

Câu 16: Tính $\lim_{x \to 2} \frac{x^{3} - 6 x^{2} + 11 x - 6}{x^{2} - 4}$ bằng?

A. $\frac{1}{4}$

B. $\frac{1}{3}$

C. $\frac{- 1}{4}$

D. − $\frac{1}{3}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

$\begin{array}{l} \lim_{x \to 2} \frac{x^{3} - 6 x^{2} + 11 x - 6}{x^{2} - 4} \\ = \lim_{x \to 2} \frac{(x - 1) (x - 2) (x - 3)}{(x - 2) (x + 2)} \\ = \lim_{x \to 2} \frac{(x - 1) (x - 3)}{(x + 2)} \\ = \frac{(2 - 1) (2 - 3)}{2 + 2} = \frac{- 1}{4} \end{array}$

Câu 17: Giá trị của giới hạn $\lim_{x \to - 1} \frac{x^{5} + 1}{x^{3} + 1}$ là:

A. $- \frac{3}{5}$

B. $\frac{3}{5}$

C. $- \frac{5}{3}$

D. $\frac{5}{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to - 1} \frac{x^{5} + 1}{x^{3} + 1} \\ = \lim_{x \to - 1} \frac{(x + 1) (x^{4} - x^{3} + x^{2} - x + 1)}{(x + 1) (x^{2} - x + 1)} \\ = \lim_{x \to - 1} \frac{x^{4} - x^{3} + x^{2} - x + 1}{x^{2} - x + 1} = \frac{5}{3} \end{array}$

Câu 18: Tính $\lim_{x \to 2} \frac{x - \sqrt{x + 2}}{\sqrt{4 x + 1} - 3}$ bằng?

A. 12.

B. $\frac{9}{8}$

C. 1.

D. $\frac{3}{4}$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\begin{array}{l} \lim_{x \to 2} \frac{x - \sqrt{x + 2}}{\sqrt{4 x + 1} - 3} \\ = \lim_{x \to 2} \frac{(x - \sqrt{x + 2}) (x + \sqrt{x + 2}) (\sqrt{4 x + 1} + 3)}{(\sqrt{4 x + 1} - 3) (\sqrt{4 x + 1} + 3) (x + \sqrt{x + 2})} \\ = \lim_{x \to 2} \frac{(x^{2} - x - 2) (\sqrt{4 x + 1} + 3)}{(4 x + 1 - 9) (x + \sqrt{x + 2})} \\ = \lim_{x \to 2} \frac{(x + 1) . (x - 2) (\sqrt{4 x + 1} + 3)}{4. (x - 2) (x + \sqrt{x + 2})} \\ = \lim_{x \to 2} \frac{(x + 1) (\sqrt{4 x + 1} + 3)}{4 (x + \sqrt{x + 2})} \\ = \frac{(2 + 1) (\sqrt{4.2 + 1} + 3)}{4. (2 + \sqrt{2 + 2})} \\ = \frac{18}{16} = \frac{9}{8} \end{array}$

Câu 19. Tính $\lim_{x \to - \infty} (x - 1) \sqrt{\frac{x^{2}}{2 x^{4} + x^{2} + 1}}$ bằng?

A. $- \frac{\sqrt{2}}{2}$

B. $\frac{\sqrt{2}}{2}$

C. $\sqrt{2}$

D. $- \sqrt{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\begin{array}{l} \lim_{x \to - \infty} (x - 1) \sqrt{\frac{x^{2}}{2 x^{4} + x^{2} + 1}} \\ = \lim_{x \to - \infty} [- \sqrt{\frac{x^{2} {(x - 1)}^{2}}{2 x^{4} + x^{2} + 1}}] \\ = \lim_{x \to - \infty} [- \sqrt{\frac{x^{2} (x^{2} - 2 x + 1)}{2 x^{4} + x^{2} + 1}}] \\ = \lim_{x \to - \infty} [- \sqrt{\frac{x^{4} - 2 x^{3} + x^{2}}{2 x^{4} + x^{2} + 1}}] \\ = \lim_{x \to - \infty} [- \sqrt{\frac{1 - \frac{2}{x} + \frac{1}{x^{2}}}{2 + \frac{1}{x^{2}} + \frac{1}{x^{4}}}}] \\ = \frac{- 1}{\sqrt{2}} = - \frac{\sqrt{2}}{2} \end{array}$

Câu 20: Giá trị của giới hạn $\lim_{x \to - 3} |\frac{- x^{2} - x + 6}{x^{2} + 3 x}|$ là:

A. $\frac{1}{3}$

B. $\frac{2}{3}$

C. $\frac{5}{3}$

D. $\frac{3}{5}$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\begin{array}{l} \lim_{x \to - 3} |\frac{- x^{2} - x + 6}{x^{2} + 3 x}| \\ = \lim_{x \to - 3} |\frac{- (x + 3) (x - 2)}{x (x + 3)}| \\ = \lim_{x \to - 3} |\frac{- (x - 2)}{x}| \\ = |\frac{- (- 3 - 2)}{- 3}| = \frac{5}{3} \end{array}$

Câu 21: Tính $\lim_{x \to 3} \frac{x^{2} - 4 x + 3}{x^{2} - 9}$ bằng?

A. 15

B. $\frac{2}{5}$

C. $\frac{1}{2}$

D. $\frac{1}{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to 3} \frac{x^{2} - 4 x + 3}{x^{2} - 9} \\ = \lim_{x \to 3} \frac{(x - 1) (x - 3)}{(x - 3) (x + 3)} \\ = \lim_{x \to 3} \frac{x - 1}{x + 3} = \frac{3 - 1}{3 + 3} \\ = \frac{1}{3} \end{array}$

Câu 22: Giá trị của giới hạn $\lim_{x \to 3^{-}} \frac{3 - x}{\sqrt{27 - x^{3}}}$ là:

A. 13.

B. 0

C. 53.

D. 35.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $3 - x > 0$ với mọi $x < 3$ , do đó:

$\begin{array}{l} \lim_{x \to 3^{-}} \frac{3 - x}{\sqrt{27 - x^{3}}} \\ = \lim_{x \to 3^{-}} \frac{3 - x}{\sqrt{(3 - x) (9 + 3 x + x^{2})}} \\ = \lim_{x \to 3^{-}} \frac{\sqrt{3 - x}}{\sqrt{9 + 3 x + x^{2}}} \\ = \frac{\sqrt{3 - 3}}{\sqrt{9 + 3.3 + 3^{2}}} = 0 \end{array}$

Câu 23: Giá trị của giới hạn $\lim_{x \to - 1} \frac{\sqrt{3 x^{2} + 1} - x}{x - 1}$ là:

A. − $\frac{3}{2}$

B. $\frac{1}{2}$

C. $- \frac{1}{2}$

D. $\frac{3}{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

$\begin{array}{l} \lim_{x \to - 1} \frac{\sqrt{3 x^{2} + 1} - x}{x - 1} \\ = \frac{\sqrt{3 + 1} + 1}{- 1 - 1} \\ = - \frac{3}{2} \end{array}$

Câu 24: Tính $\lim_{x \to - \infty} \frac{3 x^{2} - 2 x - 1}{x^{2} + 1}$ bằng?

A. −3

B. −2

C. 2

D. 3

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to - \infty} \frac{3 x^{2} - 2 x - 1}{x^{2} + 1} \\ = \lim_{x \to - \infty} \frac{3 - \frac{2}{x} - \frac{1}{x^{2}}}{1 + \frac{1}{x^{2}}} \\ = \frac{3 - 0 - 0}{1 + 0} = 3 \end{array}$

Câu 25: Kết quả của giới hạn $\lim_{x \to + \infty} \frac{\sqrt{4 x^{2} - 2 x + 1} + 2 - x}{\sqrt{9 x^{2} - 3 x} + 2 x}$ là:

A. −15.

B. +∞.

C. −∞.

D. $\frac{1}{5}$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to + \infty} \frac{\sqrt{4 x^{2} - 2 x + 1} + 2 - x}{\sqrt{9 x^{2} - 3 x} + 2 x} \\ = \lim_{x \to + \infty} \frac{x \sqrt{4 - \frac{2}{x} + \frac{1}{x^{2}}} + 2 - x}{x . \sqrt{9 - \frac{3}{x}} + 2 x} \\ = \lim_{x \to + \infty} \frac{\sqrt{4 - \frac{2}{x} + \frac{1}{x^{2}}} + \frac{2}{x} - 1}{\sqrt{9 - \frac{3}{x}} + 2} \\ = \frac{\sqrt{4 - 0 + 0} + 0 - 1}{\sqrt{9 - 0} + 2} \\ = \frac{1}{5} \end{array}$

Câu 26: Giá trị của giới hạn $\lim_{x \to + \infty} (\sqrt{x^{2} + 3 x} - \sqrt{x^{2} + 4 x})$ là:

A. $\frac{7}{2}$

B. $- \frac{1}{2}$

C. +∞.

D. −∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

$\begin{array}{l} \lim_{x \to + \infty} (\sqrt{x^{2} + 3 x} - \sqrt{x^{2} + 4 x}) \\ = \lim_{x \to + \infty} \frac{(\sqrt{x^{2} + 3 x} - \sqrt{x^{2} + 4 x}) . (\sqrt{x^{2} + 3 x} + \sqrt{x^{2} + 4 x})}{\sqrt{x^{2} + 3 x} + \sqrt{x^{2} + 4 x}} \\ = \lim_{x \to + \infty} \frac{x^{2} + 3 x - x^{2} - 4 x}{x \sqrt{1 + \frac{3}{x}} + x \sqrt{1 + \frac{4}{x}}} \\ = \lim_{x \to + \infty} \frac{- x}{x . (\sqrt{1 + \frac{3}{x}} + \sqrt{1 + \frac{4}{x}})} \\ = \lim_{x \to + \infty} \frac{- 1}{\sqrt{1 + \frac{3}{x}} + \sqrt{1 + \frac{4}{x}}} \\ = - \frac{1}{2} \end{array}$

Câu 27: Tính $\lim_{x \to 3^{+}} \frac{|x - 3|}{3 x - 9}$ bằng?

A. $- \frac{1}{3}$

B. 0.

C. $\frac{1}{3}$

D. Không tồn tại

Hiển thị đáp án

Đáp án: C

Giải thích:

Khi $x \to 3^{+}$ thì x > 3 nên x - 3> 0

$\Rightarrow |x - 3| = x - 3$

$\begin{array}{l} \lim_{x \to 3^{+}} \frac{|x - 3|}{3 x - 9} = \lim_{x \to 3^{+}} \frac{x - 3}{3 x - 9} \\ = \lim_{x \to 3^{+}} \frac{x - 3}{3 (x - 3)} = \frac{1}{3} \end{array}$

Câu 28. Trong các mệnh đề sau đâu là mệnh đề đúng?

A. $\lim_{x \to - 1} \frac{x^{2} + 3 x + 2}{|x + 1|} = - 1$

B. $\lim_{x \to - 1} \frac{x^{2} + 3 x + 2}{|x + 1|} = 0$

C. $\lim_{x \to - 1} \frac{x^{2} + 3 x + 2}{|x + 1|} = 1$

D. Không tồn tại $\lim_{x \to - 1} \frac{x^{2} + 3 x + 2}{|x + 1|}$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\begin{array}{l} \lim_{x \to - 1^{+}} \frac{x^{2} + 3 x + 2}{|x + 1|} \\ = \lim_{x \to - 1^{+}} \frac{(x + 1) (x + 2)}{x + 1} \\ = \lim_{x \to - 1^{+}} (x + 2) = - 1 + 2 = 1 \\ \lim_{x \to - 1^{-}} \frac{x^{2} + 3 x + 2}{|x + 1|} \\ = \lim_{x \to - 1^{-}} \frac{(x + 1) (x + 2)}{- (x + 1)} \\ = \lim_{x \to - 1^{-}} [- (x + 2)] \\ = - (- 1 + 2) = - 1 \\ \Rightarrow \lim_{x \to - 1^{+}} \frac{x^{2} + 3 x + 2}{|x + 1|} \neq \lim_{x \to - 1^{-}} \frac{x^{2} + 3 x + 2}{|x + 1|} \end{array}$

Suy ra, không tồn tại $\lim_{x \to - 1^{-}} \frac{x^{2} + 3 x + 2}{|x + 1|}$ .

Câu 29: Biết rằng $a + b = 4; \lim_{x \to 1} (\frac{a}{1 - x} - \frac{b}{1 - x^{3}})$ hữu hạn. . Tính giới hạn

L = $\lim_{x \to 1} (\frac{b}{1 - x^{3}} - \frac{a}{1 - x})$

A. −1

B. 2

C. 1

D. −2

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

$\begin{array}{l} \lim_{x \to 1} (\frac{a}{1 - x} - \frac{b}{1 - x^{3}}) \\ = \lim_{x \to 1} \frac{a (1 + x + x^{2}) - b}{(1 - x) . (1 + x + x^{2})} \\ = \lim_{x \to 1} \frac{a + a x + a x^{2} - b}{(1 - x) . (1 + x + x^{2})} \end{array}$

Khi đó $\lim_{x \to 1} (\frac{a}{1 - x} - \frac{b}{1 - x^{3}})$ hữu hạn thì tử thức $a + a x + a x^{2} - b$ phải có nghiệm bằng 1

⇔ $a + a .1 + a {.1}^{2} - b = 0$

$\Leftrightarrow 3 a - b = 0.$

Vậy ta có $\{\begin{cases} a + b = 4 \\ 3 a - b = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ b = 3 \end{cases}$

⇒L= $- \lim_{x \to 1} (\frac{a}{1 - x} - \frac{b}{1 - x^{3}})$

$= - \lim_{x \to 1} (\frac{1}{1 - x} - \frac{3}{1 - x^{3}})$

$\begin{array}{l} = - \lim_{x \to 1} \frac{x^{2} + x - 2}{(1 - x) . (1 + x + x^{2})} \\ = - \lim_{x \to 1} \frac{(x - 1) . (x + 2)}{(1 - x) . (1 + x + x^{2})} \\ = - \lim_{x \to 1} \frac{- (x + 2)}{1 + x + x^{2}} = 1 \end{array}$

Câu 30: Tính $\lim_{x \to 0} \frac{\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \sqrt[4]{1 + 4 x} - 1}{x}$

A. $\frac{23}{2}$

B. 24.

C. $\frac{3}{2}$

D. 3.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$\begin{array}{l} \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \sqrt[4]{1 + 4 x} - 1 \\ = \sqrt{1 + 2 x} - \sqrt{1 + 2 x} \\ + \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} \\ - \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} \\ + \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \sqrt[4]{1 + 4 x} - 1 \\ = (\sqrt{1 + 2 x} - 1) \\ + \sqrt{1 + 2 x} (\sqrt[3]{1 + 3 x} - 1) \\ + \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . (\sqrt[4]{1 + 4 x} - 1) \\ \Rightarrow \lim_{x \to 0} \frac{\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \sqrt[4]{1 + 4 x} - 1}{x} \\ = \lim_{x \to 0} (\frac{\sqrt{1 + 2 x} - 1}{x}) \\ + \lim_{x \to 0} (\sqrt{1 + 2 x} . \frac{\sqrt[3]{1 + 3 x} - 1}{x}) \\ + \lim_{x \to 0} (\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \frac{\sqrt[4]{1 + 4 x} - 1}{x}) \end{array}$

Tính:

$\begin{array}{l} \lim_{x \to 0} (\frac{\sqrt{1 + 2 x} - 1}{x}) \\ = \lim_{x \to 0} (\frac{(\sqrt{1 + 2 x} - 1) (\sqrt{1 + 2 x} + 1)}{x (\sqrt{1 + 2 x} + 1)}) \\ = \lim_{x \to 0} \frac{2 x}{x (\sqrt{1 + 2 x} + 1)} \\ = \lim_{x \to 0} \frac{2}{\sqrt{1 + 2 x} + 1} \\ = \frac{2}{1 + 1} = 1 \end{array}$

$\begin{array}{l} \lim_{x \to 0} (\sqrt{1 + 2 x .} \frac{(\sqrt[3]{1 + 3 x} - 1)}{x}) \\ = \lim_{x \to 0} (\sqrt{1 + 2 x .} \frac{(\sqrt[3]{1 + 3 x} - 1) [{(\sqrt[3]{1 + 3 x})}^{2} + \sqrt[3]{1 + 3 x} + 1]}{x [{(\sqrt[3]{1 + 3 x})}^{2} + \sqrt[3]{1 + 3 x} + 1]}) \\ = \lim_{x \to 0} (\sqrt{1 + 2 x .} \frac{3 x}{x [{(\sqrt[3]{1 + 3 x})}^{2} + \sqrt[3]{1 + 3 x} + 1]}) \\ = \lim_{x \to 0} (\frac{3 \sqrt{1 + 2 x}}{[{(\sqrt[3]{1 + 3 x})}^{2} + \sqrt[3]{1 + 3 x} + 1]}) = \frac{3.1}{1 + 1 + 1} = 1 \end{array}$

$\begin{array}{l} \lim_{x \to 0} (\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \frac{(\sqrt[4]{1 + 4 x} - 1)}{x}) \\ = \lim_{x \to 0} (\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \frac{(\sqrt[4]{1 + 4 x} - 1) [{(\sqrt[4]{1 + 4 x})}^{3} + {(\sqrt[4]{1 + 4 x})}^{2} + \sqrt[4]{1 + 4 x} + 1]}{x [{(\sqrt[4]{1 + 4 x})}^{3} + {(\sqrt[4]{1 + 4 x})}^{2} + \sqrt[4]{1 + 4 x} + 1]}) \\ = \lim_{x \to 0} (\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \frac{4 x}{x [{(\sqrt[4]{1 + 4 x})}^{3} + {(\sqrt[4]{1 + 4 x})}^{2} + \sqrt[4]{1 + 4 x} + 1]}) \\ = \lim_{x \to 0} \frac{4 \sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} .}{{(\sqrt[4]{1 + 4 x})}^{3} + {(\sqrt[4]{1 + 4 x})}^{2} + \sqrt[4]{1 + 4 x} + 1} \\ = \frac{4.1.1}{1 + 1 + 1 + 1} = 1 \end{array}$

Vậy $\lim_{x \to 0} \frac{\sqrt{1 + 2 x} . \sqrt[3]{1 + 3 x} . \sqrt[4]{1 + 4 x} - 1}{x}$

$= 1 + 1 + 1 = 3$

Câu 31: Chọn kết quả đúng trong các kết quả sau của 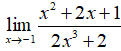Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 là:

A. -∞

B. 0

C. 1/2

D. +∞

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 32: Tìm giới hạn 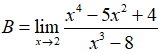Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. +∞

B. -∞

C. -1/6

D. 1

Hiển thị đáp án

Đáp án: D

Giải thích:

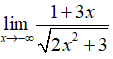
Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 33: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 bằng:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: A

Giải thích:

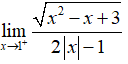
Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 34: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 bằng:

A. 3

B. 1/2

C. 1

D. √3

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 35: Tìm giới hạn 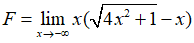Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. +∞

B. -∞

C. 4/3

D. 0

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 36: Tìm giới hạn 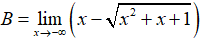Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. +∞

B. -∞

C. 4/3

D. 0

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 37: Tìm giới hạn 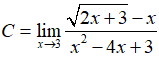Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. +∞

B. -∞

C. -1/3

D. 1

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 38: Tìm a để hàm số sau có giới hạn khi x → 2:

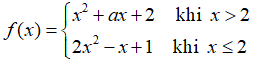
Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 .

A. +∞

B. -∞

C. 1/2

D. 1

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 39: Tìm giới hạn 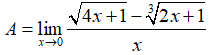Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. +∞

B. -∞

C. 4/3

D. 0

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 40: Chọn kết quả đúng của 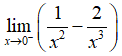Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 :

A. -∞

B. +∞

C.0

D. Không tồn tại.

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Hàm số liên tục có đáp án

Trắc nghiệm Bài ôn tập chương 4 có đáp án

Trắc nghiệm Định nghĩa và ý nghĩa của đạo hàm có đáp án

Trắc nghiệm Quy tắc tính đạo hàm có đáp án

Trắc nghiệm Đạo hàm của hàm số lượng giác có đáp án

1 1,347 12/01/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3