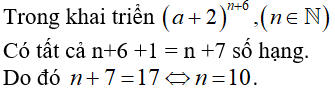TOP 40 câu Trắc nghiệm Ôn tập chương 2 (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài Ôn tập chương 2 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài Ôn tập chương 2.
Trắc nghiệm Toán 11 Bài: Ôn tập chương 2
Câu 1: Bất phương trình C4n−1−C3n−1−54A2n−2<0 có bao nhiêu nghiệm?
A. 11
B. 13
C. 6
D. Vô số
Đáp án: C
Giải thích:
Điều kiện: {n≥5n∈ℕ*.
Ta có: C4n−1−C3n−1−54A2n−2<0
⇔(n−1)!4!.(n−5)!−(n−1)!3!.(n−4)!−5(n−2)!4.(n−4)!<0
⇔n−124−n−16(n−4)−54(n−4)<0
⇔(n−1)(n−4)−4(n−1)−3024(n−4)<0
⇔n2−9n−2224(n−4)<0
⇔[n<−24<n<11.
Kết hợp điều kiện suy ra n∈{5;6;7;8;9;10}.
Câu 2: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là
A. 16
B. 60
C. 24
D. 120
Đáp án: C
Giải thích:
Xếp bạn Chi luôn ngồi chính giữa: có 1 cách.
Xếp bốn bạn còn lại vào bốn vị trí còn lại: có 4! cách.
Vậy: có 1.4!=24 cách.
Câu 3: Một hộp chứa chín chiếc thẻ được đánh số từ 1 đến 9. Lấy ngẫu nhiên (đồng thời) hai thẻ. Số phần tử của không gian mẫu là
A. 81
B. 9
C. 36
D. 72
Đáp án: C
Giải thích:
Lấy ngẫu nhiên (đồng thời) hai thẻ trong chín thẻ có: C29=36 cách.
Vậy số phần tử của không gian mẫu là C29=36.
Câu 4: Cho A={1;2;3;5;7}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau?
A. 24
B. 10
C. 125
D. 60
Đáp án: D
Giải thích:
Số các số tự nhiên gồm ba chữ số đôi một khác nhau được lập từ tập A là A35=60 số.
Vậy có: 60 số cần tìm.
Câu 5: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau?
A. 207360
B. 17280
C. 120960
D. 34560
Đáp án: C
Giải thích:
Coi 4 nữ sinh là X .
Số cách sắp xếp X và nam sinh là 7!.
Số cách sắp xếp 4 nữ sinh trong X là 4!.
Số cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau: 7!.4!=120960.
Câu 6: Từ một hộp đựng 30 thẻ được đánh số từ 1 đến 30, rút ngẫu nhiên 10 thẻ. Gọi A là biến cố rút được 5 thẻ đánh số lẻ, 5 thẻ đánh số chẵn và có đúng hai thẻ có số chia hết cho 10. Tìm số phần tử của A .
A. C313.C515.
B. 3.C313.C515.
C. 3.C312.C515.
D. C312.C515.
Đáp án: C
Giải thích:
Chọn 3 thẻ chia hết cho 10 từ các số {10;20;30} có C23 cách chọn.
Chọn 3 thẻ chẵn nhưng không chia hết cho 10 có C312 cách chọn.
Chọn 5 thẻ lẻ có C515
Suy ra có 3.C312.C515 cách chọn số phần tử của A .
Câu 7: Cho hai đường thẳng song song d1, d2. Trên d1 lấy 5 điểm phân biệt tô màu xanh, trên d2 lấy 8 điểm phân biệt tô màu đỏ. Xét tất cả các tam giác có đỉnh lấy từ các điểm trên. Chọn ngẫu nhiên một tam giác. Tính xác suất để tam giác được chọn có đúng hai đỉnh màu xanh.
A. 511
B. 5143
C. 711
D. 411
Đáp án: D
Giải thích:
Số cách chọn tam giác có đỉnh lấy từ các điểm trên là
n(Ω)=C15C28+C25C18=220
A: Biến cố tam giác được chọn có đúng hai đỉnh màu xanh
Ta có n(A)=C25C18=80
Suy ra P(A)=n(A)n(Ω)=80220=411.
Câu 8: Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT chuyên Vĩnh Phúc gồm 8 học sinh khối 10, 8 học sinh khối 11 và 8 học sinh khối 12. Nhà trường cần chọn 10 học sinh tham gia câu lạc bộ tiếng Anh của trường. Tính số cách chọn sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10.
A. 1961256.
B. 451824.
C. 451880.
D. 459888.
Đáp án: B
Giải thích:
Chọn sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10 có các khả năng sau.
TH1: Có 1 học sinh khối 10.
Số cách chọn trong trường hợp này là C18.C916=91520.
TH2: Có 2 học sinh khối 10.
Số cách chọn trong trường hợp này là C28.(C816−2.C88)=360304.
Vậy áp dụng quy tắc cộng ta có 91520+360304=451824.
Câu 9: Có 3 xạ thủ bắn độc lập vào bia. Xác suất bắn trúng của mỗi xạ thủ lần lượt là 0,6; 0,8 và 0,9. Tính xác suất để trong 3 xạ thủ có đúng 2 xạ thủ bắn trúng bia.
A. 0,568.
B. 0,876.
C. 0,7.
D. 0,444.
Đáp án: D
Giải thích:
Gọi Ai với i=1,2,3 là các biến cố xạ thủ thứ i bắn trúng bia.
Theo giả thiết, ta có P(A1)=0,6; P(A2)=0,8; P(A1)=0,9.
Khi đó, xác suất để trong 3 xạ thủ có đúng 2 xạ thủ bắn trúng bia là
P=P(A1).P(A2).P(¯A3)
+P(A1).P(¯A2).P(A3)
+P(¯A1).P(A2).P(A3)
⇔P=0,444.
Câu 10: Hệ số x7 của trong khai triển (4−x)9 là
A. 9C79.
B. −16C79.
C. −9C79.
D. 16C79.
Đáp án: D
Giải thích:
Số hạng tổng quát của khai triển: Ck9(−1)k49−kxk
Ta có xk=x7⇔k=7.
Hệ số trước x7 là −C7942.
Câu 11: Từ các chữ số 0 ; 1; 2 ; 3 ; 5 lập được bao nhiêu số gồm có 4 chữ số khác nhau và không chia hết cho 5 ?
A. 54.
B. 120.
C. 69.
D. 72.
Đáp án: A
Giải thích:
Gọi số cần tìm là ¯abcd với a≠0, a≠b≠c≠d.
d∈{1;2;3}⇒d có 3 cách chọn.
a≠0 và a≠d , nên a có 3 cách chọn.
Chọn b và c có A23 cách chọn.
Vậy cách 3.3.A23=54 cách.
Câu 12: Giải bóng đá ngoại hạng Anh có 20 đội bóng tham gia thi đấu vòng tròn 2 lượt. Hỏi có bao nhiêu trận đấu sẽ được tổ chức?
A. 40.
B. 190.
C. 380.
D. 400.
Đáp án: C
Giải thích:
Cứ hai đội gặp nhau cho ta một trận đấu nên số trận đấu một lượt là C220.
Số trận đấu hai lượt là C220.2=380 trận.
Câu 13: Trong 1 hộp đựng 4 viên bi đỏ và 3 viên bi xanh, lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy ra 2 viên cùng màu?
A. 7.
B. 6.
C. 9.
D. 3.
Đáp án: C
Giải thích:
Nếu lấy 2 viên có cùng màu đỏ thì có C24=6.
Nếu lấy 2 viên có cùng màu xanh thì có C23=3.
Vậy có C24+C23=6+3=9.
Câu 14: Tổng C12017+C22017+...+C20162017 bằng
A. 22017+1.
B. 22016+1.
C. 22017−1.
D. 22017−2.
Đáp án: D
Giải thích:
Xét tổng (x+1)2017=∑2017k=0Ck2017xk
⇔(1+1)2017
=C02017+C12017+...+C20162017+C20172017.
⇔22017
=1+C12017+C22017+...+C20162017+1
⇔22017−2
=C12017+C22017+...+C20162017.
Câu 15: Số hạng thứ 6 trong khai triển (1−3x)12 theo lũy thừa tăng dần của x
A. C512.37.
B. −C512.(−3)5.x5.
C. C512.37.x6.
D. −C512.35.x5.
Đáp án: D
Giải thích:
Ta có: (1−3x)12=∑12k=0Ck12(−3)kxk
Số hạng thứ 6 ứng với là C512.(−3)5.x5
Câu 16: Trên giá sách của bạn Minh có 4 quyển truyện khác nhau và 6 quyển tạp chí khác nhau. Bạn Minh chọn một quyển truyện hoặc một quyển tạp chí để cho bạn Sáng mượn. Hỏi bạn Minh có bao nhiêu cách chọn.
A. 6.
B. 10.
C. 24.
D. 4.
Đáp án: B
Giải thích:
Số cách bạn Minh chọn một quyển truyện cho bạn Sáng mượn là 4 cách.
Số cách bạn Minh chọn một quyển tạp chí cho bạn Sáng mượn là 6 cách.
Vậy bạn Minh có 4+6=10cách chọn một quyển truyện hoặc một quyển tạp chí để cho bạn Sáng mượn.
Câu 17: Có bao nhiêu cách sắp xếp năm bạn An, Bình, Châu, Dung và Đức đứng thành một hàng ngang?
A. 25.
B. 20.
C. 120.
D. 24.
Đáp án: C
Giải thích:
Số cách sắp xếp năm bạn thành một hàng ngang là các hoán vị của năm phần tử có 5!=120 cách.
Câu 18: Cho tập hợp M có 12 phần tử. Số tập con gồm 3 phần tử của M là
A. A912
B. C312
C. A312
D. 123
Đáp án: B
Giải thích:
Số tập con gồm 3 phần tử của M là số cách chọn 3 phần tử không phân biệt thứ tự từ 12 phần tử.
Vậy có C312. tập hợp.
Câu 19: Cho khai triển (1+2x)10=a0+a1x+...+a10x10. Khi đó giá trị của a1 bằng bao nhiêu?
A. a1=320
B. a1=10
C. a1=20
D. a1=5120
Đáp án: C
Giải thích:
Tk+1=Ck10110−k.(2x)k
=Ck10.2k.xk
a1 là hệ số ứng với x⇒k=1.
Vậy a1=C110.21=20.
Câu 20: Công thức nào sau đây sai?
A. Akn=n!(n−k)!
B. Ckn=n!k!+(n−k)!
C. kCkn=nCk−1n−1
D. Ckn=Cn−kn
Đáp án: B
Giải thích:
Ckn=n!k!(n−k)!.
Câu 21: Số cách sắp xếp 4 nam sinh và 3 nữ sinh vào một dãy ghế hàng ngang có 7 chỗ ngồi là
A. 7!
B. 4!.3!
C. 12!
D. 4!+3!
Đáp án: A
Giải thích:
Số cách sắp xếp 7 học sinh vào dãy ghế hang ngang có 7!.
Câu 22: Giá trị của tổng A=C12016+C22016+...C20152016 bằng
A. 22016
B. 22016−1
C. 22016−2
D. 42016
Đáp án: C
Giải thích:
Khai triển nhị thức:
(l+x)2016
=C02016+x.C12016+x2.C22016+....+x2015.C20152016+x2016.C20162016.
Thay x=1 vào nhị thức trên ta được:
(l+1)2016=C02016+C12016+C22016+....+C20152016+C20162016.
Từ đó suy ra:
C12016+C22016+....+C20152016
=22016−C02016−C20162016
⇔C12016+C22016+....+C20152016
=22016−2.
Câu 23: Một hộp chứa 6 viên bi gồm 3 viên bi xanh, 2 viên bi vàng và 1 viên bi trắng. Lấy ngẫu nhiên 3 viên bi từ hộp đó. Tính xác suất để lấy được ba viên bi có đủ ba màu.
A. 12
B. 320
C. 112
D. 310
Đáp án: D
Giải thích:
Số phần tử không gian mẫu n(Ω)=C36=20.
Gọi A là biến cố lấy được ba viên bi có đủ ba màu.
Ta có n(A)=C13.C12.C11=6
⇒P(A)=620=310.
Câu 24: Gieo hai con súc sắc cân đối đồng chất. Tính xác suất để hiệu số chấm xuất hiện của hai con súc sắc bằng 1.
A. 536
B. 59
C. 518
D. 19
Đáp án: C
Giải thích:
Số phần tử không gian mẫu n(Ω)=6.6=36.
Gọi A là biến cố hiệu số chấm xuất hiện của hai con súc sắc bằng 1.
A={(1;2),(2;1),(2;3),(3;2),(3;4),(4;3),(4;5),(5;4),(5;6),(6;5)}
⇒n(A)=10⇒P(A)=1036=518.
Câu 25: Có ba chiếc hộp mỗi hộp đựng 2 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 1 viên bi xanh?
A. 5121000
B. 4881000
C. 115
D. 130
Đáp án: B
Giải thích:
Gọi Ω là không gian mẫu của phép thử.
Số cách lấy mỗi hộp một viên bi: 10.10.10=1000(cách).
Suy ra, số phần tử của Ω là n(Ω)=1000 (cách)
Gọi A là biến cố: “Trong 3 viên bi lấy được có ít nhất 1 viên bi xanh”
Suy ra là biến cố: “Trong 3 viên bi lấy được không có viên bi xanh”
Số cách lấy mỗi hộp một viên bi sao cho không có bi xanh:8.8.8=512 (cách).
⇒n(ˉA)=512 (cách)
Suy ra xác suất cần tìm:
P(A)=1−P(ˉA)=1−5121000=4881000.
Câu 26: Cho đa giác đều có 14 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác. Tính xác suất để 3 đỉnh được chọn là 3 đỉnh của một tam giác vuông.
A. 413
B. 313
C. 513
D. 213
Đáp án: B
Giải thích:
Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác
⇒n(Ω)=C314=364.
Gọi A là biến cố: "3 đỉnh được chọn là 3 đỉnh của tam giác vuông"
Chọn một đường chéo đi qua tâm, có 7 cách chọn.
Tương ứng với mỗi đường kính ấy, mỗi đỉnh còn lại sẽ tạo với đường kính một tam giác vuông. Khi đó, số tam giác vuông được tạo ra là
7.C112=84⇒n(A)=84.
Vậy xác suất cần tính là P(A)=n(A)n(Ω)=313.
Câu 27: Một tổ học sinh có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ.
A. 815
B. 215
C. 715
D. 13
Đáp án: B
Giải thích:
Chọn 2 học sinh bất kì từ 10 học sinh có C210=45 (cách chọn).
Chọn 2 học sinh nữ từ 4 học sinh nữ có C24=6 (cách chọn).
Vậy xác suất cần tính là P=645=215.
Câu 28: Một bình đựng 8 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi trong bình. Xác suất để có được ít nhất hai viên bi xanh là
A. 4155
B. 2855
C. 4255
D. 1455
Đáp án: C
Giải thích:
Lấy ngẫu nhiên 3 viên bi trong bình thì số phần tử của không gian mẫu là C312=220.
Gọi A là biến cố “được ít nhất hai viên bi xanh”.
Ta có số phần tử thuận lợi cho biến cố A là C28.C14+C38=168.
Vậy xác suất của A là 168220=4255.
Câu 29: Một trường THPT có 4 học sinh giỏi toán là nam, 5 học sinh giỏi văn là nam và 3 học sinh giỏi văn là nữ. Cần chọn 3 em đi dự đại hội ở Tỉnh. Tính xác suất để trong 3 em được chọn có cả nam lẫn nữ, có cả học sinh giỏi toán và học sinh giỏi văn.
A. 344
B. 322
C. 922
D. 1855
Đáp án: C
Giải thích:
Chọn 3 trong tổng số 12 học sinh: n(Ω)=C312=220.
Trong 3 em được chọn có cả nam lẫn nữ, có cả học sinh giỏi toán và học sinh giỏi văn:
+ Chọn 1 toán nam, 2 văn nữ: n(A)=C14.C23=12.
+ Chọn 1 toán nam, 1 văn nam, 1 văn nữ: n(A)=C14.C15.C13=60.
+ Chọn 2 toán nam, 1 văn nữ: n(A)=C24.C13=18.
⇒n(A)=12+60+18=90.
⇒P(A)=n(A)n(Ω)=90220=922.
Câu 30: Tìm hệ số lớn nhất trong khai triển (a+b)n biết tổng các hệ số bằng 4096.
A. 792.
B. 462.
C. 924.
D. 1716.
Đáp án: C
Giải thích:
Chọn a=b=1 ta có 2n=4096⇒n=12.
Khi đó ta có:
212=C012+C112+C312+........+C1212.
Hệ số của số hạng thứ 7 là hệ số lớn nhất bằng C612=924.
Câu 31: Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là:
A. 480
B. 24
C. 48
D. 60
Đáp án: B
Giải thích:
Nếu chọn một cây bút chì thì sẽ có 8 cách. Nếu chọn một cây bút bi thì sẽ có 6 cách. Nếu chọn một cuốn tập thì sẽ có 10 cách. Theo qui tắc cộng, ta có 8 + 6+ 10 = 24 cách chọn.
Câu 32: Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hóa. Mỗi thí sinh được quyền chọn một đề tài. Hỏi mỗi thí sinh có bao nhiêu khả năng lựa chọn đề tài?
A. 20
B. 3360
C. 31
D. 30
Đáp án: C
Giải thích:
Nếu chọn đề tài về lịch sử có 8 cách. Nếu chọn đề tài về thiên nhiên có 7 cách. Nếu chọn đề tài về con người có 10 cách. Nếu chọn đề tài về văn hóa có 6 cách. Theo qui tắc cộng, ta có 8+ 7+ 10 + 6 = 31 cách chọn.
Câu 33: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.
A. 240
B. 210
C. 18
D. 120
Đáp án: B
Giải thích:
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có: Có 5 cách chọn hoa hồng trắng. Có 6 cách chọn hoa hồng đỏ. Có 7 cách chọn hoa hồng vàng. Vậy theo qui tắc nhân ta có 5.6.7= 210 cách.
Câu 34: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món ăn trong 5 món, một loại quả tráng miệng trong 5 loại quả tráng miệng và một nước uống trong 3 loại nước uống. Có bao nhiêu cách chọn thực đơn.
A. 25
B. 75
C. 100
D. 15
Đáp án: B
Giải thích:
Để chọn thực đơn, ta có: Có 5 cách chọn món ăn. Có 5 cách chọn quả tráng miệng. Có 3 cách chọn nước uống. Vậy theo qui tắc nhân ta có 5.5.3 = 75 cách.
Câu 35: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.
A. 240
B. 210
C. 18
D. 120
Đáp án: B
Giải thích:
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.
Câu 36: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món ăn trong năm món, một loại quả tráng miệng trong năm loại quả tráng miệng và một nước uống trong ba loại nước uống. Có bao nhiêu cách chọn thực đơn.
A. 25
B. 75
C. 100
D. 15
Đáp án: B
Giải thích:
Để chọn thực đơn, ta có:
Có 5 cách chọn món ăn.
Có 5 cách chọn quả tráng miệng.
Có 3 cách chọn nước uống.
Vậy theo qui tắc nhân ta có 5.5.3 = 75 cách.
Câu 37: Có bao nhiêu cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài?
A.15
B. 720
C. 30
D. 360
Đáp án: D
Giải thích:
Số cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài là một chỉnh hợp chập 4 của 6 phần tử.
Suy ra có 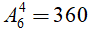
Câu 38: Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ thì có bao nhiêu cách chọn?
A. 210
B. 200
C. 180
D. 150
Đáp án: A
Giải thích:
Số cách chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử.
Vậy có 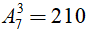
Câu 39: Trong khai triển nhị thức (a + 2)n + 6, (n ∈ N). Có tất cả 17 số hạng. Vậy n bằng:
A. 17
B. 11
C. 10
D. 12
Đáp án: C
Giải thích:
Câu 40: Tìm hệ số của x5 trong khai triển P(x) = x(1 - 2x)5 + x2(1 + 3x)10
A. 80
B. 3240
C. 3320
D. 259200
Đáp án: C
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Phương pháp quy nạp toán học có đáp án
Trắc nghiệm Cấp số cộng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án