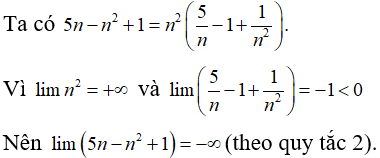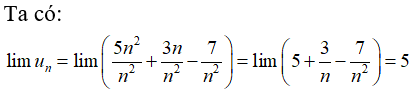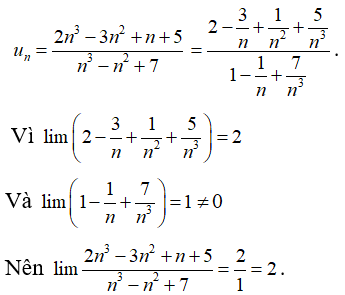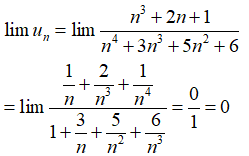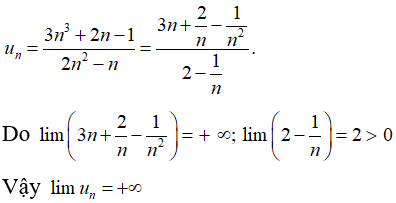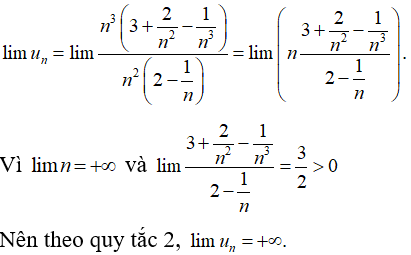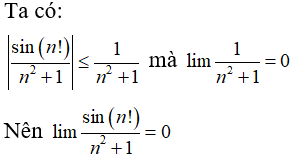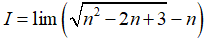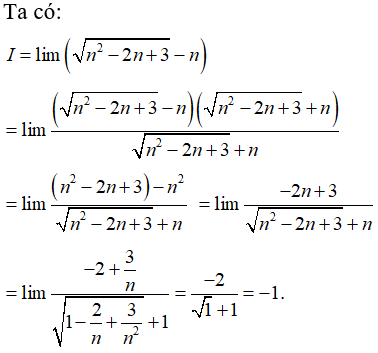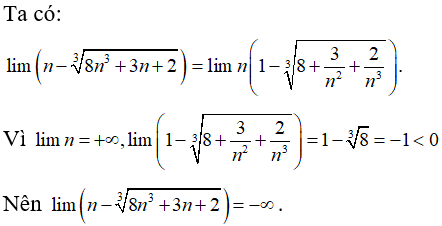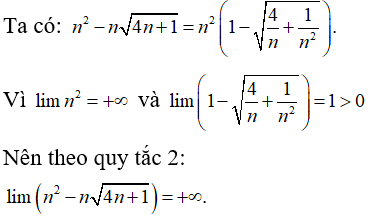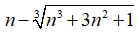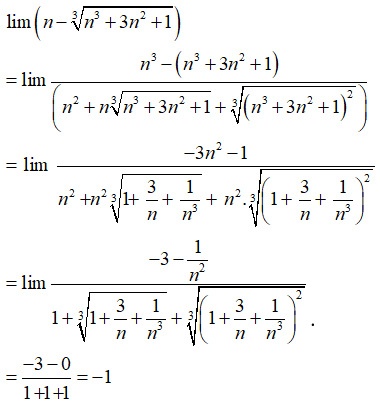TOP 40 câu Trắc nghiệm Giới hạn của dãy số (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 1: Giới hạn của dãy số có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 1.
Trắc nghiệm Toán 11 Bài 1: Giới hạn của dãy số
Bài giảng Trắc nghiệm Toán 11 Bài 1: Giới hạn của dãy số
Câu 1: Cho cấp số nhân un=12n∀n≥1un=12n∀n≥1 .Khi đó:
A. S=1
B. S=12n
C. S=0
D. S=2
Đáp án: A
Giải thích:
Cấp số nhân đã cho là cấp số nhân lùi vô hạn có:
u1=12;q=12
⇒S=u11−q=121−12=1
Câu 2: Dãy số nào sau đây có giới hạn 0 ?
A. un=n2
B. un=2n
C. un=n
D. un=√n
Đáp án: B
Giải thích:
Dãy số (un) mà un=2n có giới hạn 0.
Câu 3: Cho (un) là một cấp số nhân công bội q=13 và số hạng đầu u1=2,
Đặt S=u1+u2+...+un . Giá limSn là:
A. 1
B. 23
C. 43
D. 3
Đáp án: D
Giải thích:
Do 0<q=13<1 nên cấp số nhân đã cho là cấp số nhân lùi vô hạn:
S=u1+u2+...+un
=u1(1−qn)1−q
⇒limSn=u1(1−qn)1−q
=u11−q=21−13=3
Câu 4: Cấp số nhân (un) có u1=2,u2=1. Đặt Sn=u1+u2+...+un ), khi đó:
A. Sn=4(1−12n)
B. Sn=4
C. Sn=2
D. Sn=(1−12n)
Đáp án: A
Giải thích:
Vì Sn=u1+u2+...+un nên đây là tổng n số hạng đầu của cấp số nhân công bội
q= u2u1= 12.
Theo công thức tính tổng Sn=u1(1−qn)1−q ta được:
Sn=2(1−(12)n)1−12=4(1−12n)
Câu 5: Giá trị của C=lim√3.3n+4n3n+1+4n+1 bằng:
A. +∞
B. 12
C. 0
D. 1
Đáp án: B
Giải thích:
C=lim√3.3n+4n3n+1+4n+1
=lim√3.3n+4n3.3n+4.4n
=lim√3.(34)n+13.(34)n+4
=√3.0+13.0+ 4=12
Câu 6: Biết limun=3. Chọn mệnh đề đúng trong các mệnh đề sau.
A. lim3un−1un+1=3
B. lim3un−1un+1=−1
C. lim3un−1un+1=2
D. lim3un−1un+1=1
Đáp án: C
Giải thích:
Ta có:
lim3un−1un+1=3limun−1limun+1
=3.3−13+1=84=2
Câu 7: Biết limun=+∞. Chọn mệnh đề đúng trong các mệnh đề sau.
A. limun+13u2n+5=1
B. limun+13u2n+5=0
C. limun+13u2n+5=13
D. limun+13u2n+5=+∞
Đáp án: B
Giải thích:
Ta có :
limun+13u2n+5=limu2n(1un+1u2n)u2n(3+5u2n)
=lim(1un+1u2n)(3+5u2n)=0+03+0=0
Câu 8: Cho hai dãy số (un) , (vn) với un=1n,vn=(−1)nn.
Biết |(−1)nn|≤1n. Chọn kết luận không đúng:
A. limun=0
B. limvn=0
C. limun−limvn=0
D. Không tồn tại
Đáp án: D
Giải thích:
Dễ thấy limun=0 nên A đúng.
Do |(−1)nn|≤1n và lim1n=0 nên
lim(−1)nn=0 hay limvn=0
Do đó các đáp án B và C đúng.
Câu 9: Giới hạn lim(3.2n+1−5.3n+7n) bằng :
A. −∞.
B. +∞.
C. 3.
D. −5.
Đáp án: A
Giải thích:
Ta có:
lim(3.2n+1−5.3n+7n)
=lim(6.2n−5.3n+7n)
=lim3n(6(23)n−5+7n3n)
=−∞
Vì lim 3n= + ∞;
lim(6(23)n−5+7n3n)
=6.0−5+7.0= −5< 0
Câu 10: Giới hạn lim(2−5n)3(n+1)22−25n5 bằng?
A. −4.
B. −1.
C. 5.
D. −32.
Đáp án: C
Giải thích:
lim(2−5n)3(n+1)22−25n5
=lim(2−5n)3n3.(n+1)2n22−25n5n5
=lim(2−5nn)3.(n+1n)22n5−25
lim(2n−5)3.(1+ 1n)22n5−25
=(0−5)3(1+0)20−25
=(−5)3.12−25=5
Câu 11: Giá trị của lim(2n2+1)4(n+2)9n17+1 bằng:
A. +∞
B. −∞
C. 16
D. 1
Đáp án: C
Giải thích:
Ta có:
C=limn8(2+1n2)4.n9(1+2n)9n17(1+1n17)
=lim(2+1n2)4(1+2n)91+1n17
= (2+0)4.(1+0)91+ 0
=24.11=16
Câu 12: Chọn kết luận không đúng:
A. lim12n=0
B. lim13n=0
C. lim10,5n=0
D. lim1(√2)n=0
Đáp án: C
Giải thích:
Ta thấy:
12n=(12)n;13n=(13)n;
1(0,5)n=(10,5)n=2n;
1(√2)n=(1√2)n
Mà 12<1;13<1;1√2<1 nên các đáp án A, B, D đúng.
Vì 2>1 nên lim2n=+∞ nên C sai.
Câu 13: Cho dãy số (un) có giới hạn L=−12. Chọn kết luận đúng:
A. lim(un+12)=12
B. lim(un+12)=0
C. lim(un−12)=0
D. lim(un−12)=12
Đáp án: B
Giải thích:
Vì limun=−12 nên lim(un+12)=0
Câu 14: Cho dãy số (un) với un=(1−122).(1−132)...(1−1n2). Khi đó lim(un) bằng?
A. 43
B. 12
C. 1.
D. 2
Đáp án: B
Giải thích:
un=(1−122).(1−132)...(1−1n2)
=(22−122).(32−132)...(n2−1n2)
=(22−1)(32−1)...(n2−1)2.232...n2
=(1.3)(2.4)(3.5)(4.6)...[(n−1)(n+1)]2.232...n2
=n+12n
⇒limun=limn+12n
=lim1+1n2=12
Câu 15: Giá trị của D=lim(√n2+2n−3√n3+2n2) bằng:
A. +∞
B. −∞
C. 13
D. 1
Đáp án: C
Giải thích:
Ta có:
D=lim(√n2+2n−3√n3+2n2)=lim(√n2+2n−n)−lim(3√n3+2n2−n)=limn2+2n−n2√n2+2n+n−limn3+2n2−n33√(n3+2n2)2+n3√n3+2n2+n2=lim2n√n2+2n+n−lim2n23√(n3+2n2)2+n3√n3+2n2+n2=lim2√1+2n+1−lim23√(1+2n)2+3√1+2n+1=22−21+1+1=13
Câu 16: Cho các dãy số (un), (vn)có limun=53, limvn=−23. Chọn đáp án đúng:
A. lim(un−2vn)=13
B. lim(2un−vn)=4
C. lim(un−vn)=1
D. lim(un+vn)=13
Đáp án: B
Giải thích:
Đáp án A:
lim(un−2vn)=53−2(−23)
=3≠13 nên A sai.
Đáp án B:
lim(2un−vn)=2.53−(−23)=4
nên B đúng.
Đáp án C:
lim(un−vn)=53−(−23)
=73≠1 nên C sai.
Đáp án D:
lim(un+vn)=53+(−23)
=1≠13 nên D sai.
Câu 17: Cho un=1−4n5n. Khi đó lim un bằng?
A. 15
B. −45
C. 45
D. −15
Đáp án: B
Giải thích:
limun=lim1−4n5n
=lim1n−45=0−45
=−45
Câu 18: Cho un=n2−3n1−4n3. Khi đó limun bằng?
A. 0
B. −14
C. 34
D. −34
Đáp án: A
Giải thích:
limun=limn2−3n1−4n3
=lim1n−3n21n3−4=0−00−4=0
Câu 19: Cho un=3n+5n5n. Khi đó limun bằng?
A. 0.
B. 1.
C. 35.
D. +∞.
Đáp án: B
Giải thích:
limun=lim3n+5n5n
=lim(35)n+11
=0+ 11=1
Câu 20: Giá trị lim(n3−2n+1) bằng
A. 0
B. 1
C. −∞
D. +∞
Đáp án: D
Giải thích:
Ta có:
n3−2n+1
=n3(1−2n2+1n3)
Vì limn3=+∞ và
lim(1−2n2+1n3)
=1−0+ 0=1>0
nên lim(n3−2n+1)=+∞
Câu 21: Giá trị lim(5n−n2+1) bằng
A. +∞
B. −∞
C. 5
D. −1
Đáp án: B
Giải thích:
Ta có :
5n−n2+1
=n2(−1+5n+1n2)
Vì limn2=+∞ và lim(−1+5n+1n2)=−1<0
nên lim(5n−n2+1)=−∞
Câu 22. Giới hạn lim(√n2−n−n) bằng?
A. −∞.
B. −12.
C. 0.
D. +∞.
Đáp án: B
Giải thích:
lim(√n2−n−n)
=lim(√n2−n−n)(√n2−n+n)(√n2−n+n)
=limn2−n−n2(√n2−n+n)
=lim−n(√n2−n+n)
=lim−n(n√1−1n+n)
=lim−1√1−1n+1
=−11+1=−12
Câu 23: Giá trị của B=lim(3√n3+9n2−n) bằng:
A. +∞
B. −∞
C. 0
D. 3
Đáp án: D
Giải thích:
Ta có:
B=lim(3√n3+9n2−n)=limn3+9n2−n33√(n3+9n2)2+n3√n3+9n2+n2=lim9n23√(n3+9n2)2+n3√n3+9n2+n2=lim9n2n23√(1+ 9n)2+n2.3√1+ 9n+n2=lim93√(1+9n)2+3√1+9n+1=91+1+1=3
Câu 24: Cho dãy số (un) với
un=11.3+13.5+...+1(2n−1)(2n+1)+ 1. Khi đó lim(un)bằng?
A. 12
B. 14
C. 1
D. 2
Đáp án: A
Giải thích:
un=11.3+13.5+...+1(2n−1)(2n+1)=12.(1−13+13−15+...+12n−1−12n+1)=12(1−12n+1)⇒limun=lim12(1−12n+1)=12
Câu 25: Giá trị lim(−1)nn(n+1) bằng
A. −1.
B. 1.
C. +∞.
D. 0.
Đáp án: D
Giải thích:
Ta có:
|(−1)nn(n+1)|=1n(n+1)<1n.n=1n2
mà lim1n2=0 nên suy ra lim(−1)nn(n+1)=0
Câu 26. Giới hạn lim(√n2−n+1−√n2+1) bằng?
A. 0.
B. −12
C. −1√2
D. 1√2
Đáp án: B
Giải thích:
lim(√n2−n+1−√n2+1)=limn2−n+1−n2−1(√n2−n+1+√n2+1)=lim−nn.√1−1n+1n2+n.√1+1n2=lim−1√1−1n+1n2+√1+1n2=−1√1−0+0+ √1+0=−12
Câu 27: Giới hạn lim2n2−n+4√2n4−n2+1 bằng?
A. 1
B. √2
C. 2
D. 1√2
Đáp án: B
Giải thích:
lim2n2−n+4√2n4−n2+1=lim n2.(2−1n+4n2)n2.√2−1n2+1n4 =lim2−1n+4n2√2−1n2+1n4=2−0+0√2−0+0=√2
Câu 28: Cho các số thực a, b thỏa |a|<1;|b|<1.
Tìm giới hạn I=lim1+a+a2+...+an1+b+b2+...+bn
A. +∞
B. 1−a1−b
C. 1−b1−a
D. 1
Đáp án: C
Giải thích:
Ta có 1,a,a2,...,an là một cấp số nhân có công bội q = a
⇒1+a+a2+...+an=1−an+11−a
Tương tự:
1+b+b2+...+bn=1−bn+11−b
⇒limI=lim1−an+11−a1−bn+11−b=lim(1−an+11−a.1−b1−bn+1)=lim(1−an+11−bn+1.1−b1−a)=1−b1−a
(Vì|a|<1,|b|<1
⇒liman+1=limbn+1=0
Câu 29: Cho dãy số (un) xác định bởi {u1=2un+1=un+12,(n≥1). Khi đó mệnh đề nào sau đây là đúng?
A. Dãy (un) là dãy giảm tới 1 khi n→+∞.
B. Dãy (un) là dãy tăng tới 1 khi n→+∞.
C. Không tồn tại giới hạn của dãy (un).
D. Cả 3 đáp án trên đều sai.
Đáp án: C
Giải thích:
u2=2+12=32=21+121u3=32+12=54=22+122u4=54+12=98=23+123
Chứng minh bằng quy nạp:
un+1=2n+12n,∀n=1,2,...(*);
* Với n=1;
u2=u1+12=2+12=21+121:(*) đúng
* Giả sử (*) đúng với n=k≥1, tức là uk=2k+12k ta chứng minh (*) đúng với n=k+1,
tức là cần chứng minh uk+1=2k+1+12k+1
Ta có :
uk+1=uk+12=2k+12k+12=2k+1+2k2k2=2.2k+12.2k=2k+1+12k+1
Theo nguyên lý quy nạp, ta chứng minh được (*).
Như vậy, công thức tổng quát của dãy là:
un=2n−1+12n−1
=1+12n−1, ∀n=1;2;... (∗)
Từ (*) ta có
un+1−un=1+12n−(1+12n−1)=12n−12n−1<0∀n=1,2,..
⇒ (un) là dãy giảm và limun=lim(1+12n−1)=1
⇒(un) là dãy giảm tới 1 khi n→+∞
Câu 30: Tính giới hạn của dãy số un=q+2q2+...+nqn với |q|<1
A. +∞
B. −∞
C. q(1−q)2
D. q(1+q)2
Đáp án: C
Giải thích:
Ta có:
un-qun=q+2q2+⋯-q(q+2q2+⋯nqn)
=q+q2+q3+⋯+qn-nqn+1
Do q,q2,q3,...,qn là cấp số nhân có công bội q nên:
un−qun
=q.(1−qn)1−q−nqn+1 (1)
Mà: un−qun=(1−q)un (2)
Từ (1); (2) suy ra:
(1−q).un
= q.(1−qn)1−q−nqn+1
=>un=q.1−qn(1−q)2−nqn+11−q
Do |q|<1 nên limqn+1=0;
limqn=0
Suy ra
un=lim[q(1−qn)(1−q)2−n.qn+11−q]=q(1−q)2
Câu 31: Tính lim(5n - n2 + 1)
A. +∞
B. -∞
C. 5.
D. -1
Đáp án: B
Giải thích:
Câu 32: Tính lim un, với 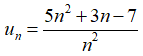
A. 5
B. 0
C. 3
D. - 7
Đáp án: A
Giải thích:
Câu 33: Tính lim un với 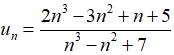
A. – 3
B. 1
C. 2
D. 0
Đáp án: C
Giải thích:
Chia cả tử và mẫu của phân thức cho n3 (n3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
Câu 34: Giới hạn của dãy số (un) với 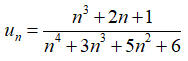
A. 1
B. 0
C. +∞
D. -∞
Đáp án: B
Giải thích:
Chia cả tử và mẫu của phân thức cho n4 (n4 là bậc cao nhất của n trong phân thức), ta được
Câu 35: Giới hạn của dãy số (un) với 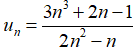
A. 3/2
B. 0
C. +∞.
D. 1
Đáp án: C
Giải thích:
Cách 1: Chia cả tử và mẫu cho n2 (n2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được :
Cách 2:
Ta có:
Chọn đáp án C
Câu 36: 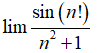
A. 0
B. 1
C. +∞
D. 2
Đáp án: A
Giải thích:
Câu 37: Tính giới hạn
A. I = -1
B. I = 1
C. I = 0
D. I = +∞
Đáp án: A
Giải thích:
Câu 38: 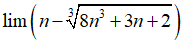
A. +∞
B. -∞
C. -1
D. 0
Đáp án: B
Giải thích:
Câu 39: 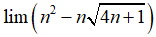
A. – 1
B. 3
C. +∞
D. -∞
Đáp án: C
Giải thích:
Câu 40: 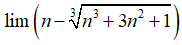
A. – 1
B. 1
C. +∞
D. -∞
Đáp án: A
Giải thích:
Ta tiến hành nhân chia với biểu thức liên hợp (bậc ba) của
Chọn đáp án A
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Giới hạn của hàm số có đáp án
Trắc nghiệm Hàm số liên tục có đáp án
Trắc nghiệm Bài ôn tập chương 4 có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án