TOP 40 câu Trắc nghiệm Phép đồng dạng (có đáp án 2023) – Toán 11

Trắc nghiệm Toán 11 Bài 8: Phép đồng dạng

Bài giảng Trắc nghiệm Toán 11 Bài 8: Phép đồng dạng

Câu 1: Cho hình vẽ sau :

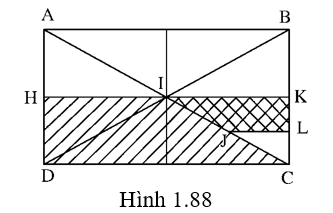
Xét phép đồng dạng biến hình thang HICD thành hình thang LJIK. Tìm khẳng định đúng :

A. Phép đối xứng trục Đ_ACvà phép vị tự $V_{\left(B,2\right)}$.

B. Phép đối xứng tâm Đ_I phép vị tự $V_{\left(C,\frac{1}{2}\right)}$.

C. Phép tịnh tiến $T_{\overrightarrow{AB}}$ và phép vị tự $V_{\left(I,2\right)}$.

D. Phép đối xứng trục Đ_BD và phép vị tự $V_{\left(B,-2\right)}$.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có:

${\text{D}}_I:HICD\mapsto KIAB;$

$V_{\left(C,\frac{1}{2}\right)}\text{:}KIAB\mapsto LJIK$

Do đó ta chọn đáp án B

Câu 2: Cho $\Delta ABC$ đều cạnh 2. Qua ba phép đồng dạng liên tiếp : Phép tịnh tiến $T_{\overrightarrow{BC}}$, phép quay $Q\left(B,{60}^o\right)$, phép vị tự $V_{\left(A,3\right)}$, $\Delta ABC$ biến thành $\Delta A_1{B}_1{C}_1$. Diện tích $\Delta A_1{B}_1{C}_1$ là :

A. $5\sqrt{2}$

B. $9\sqrt{3}$

C. $9\sqrt{2}$

D. $5\sqrt{3}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Do phép tịnh tiến và phép quay bảo toàn khoảng cách giữa các cạnh nên phép tịnh tiến $T_{\overrightarrow{BC}}$, phép quay $Q\left(B,{60}^o\right)$, phép vị tự $V_{\left(A,3\right)}$, $\Delta ABC$ biến thành $\Delta A_1{B}_1{C}_1$ thì  

$A_1{B}_1=3AB=6$

Tam giác đều $\Delta A_1{B}_1{C}_1$ có cạnh bằng 6

$\Rightarrow S_{\Delta A_1{B}_1{C}_1}=\frac{6^2\sqrt{3}}{4}=9\sqrt{3}$ .

Câu 3: Mọi phép dời hình cũng là phép đồng dạng tỉ số

A. k= 1

B. k= -1

C. k= 0

D. k= 3

Hiển thị đáp án  

Đáp án: A

Giải thích:

Theo tính chất của phép đồng dạng.

Câu 4: Trong các mệnh đề sau đây mệnh đề nào sai?

A. Phép dời là phép đồng dạng tỉ số k= 1

B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

C. Phép vị tự tỉ số k là phép đồng dạng tỉ số $\left|k\right|$

D. Phép đồng dạng bảo toàn độ lớn góc.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Vì phép quay là phép đồng dạng mà phép quay với góc quay $\alpha \ne k\pi \left(k\in \mathbb{Z}\right)$ thì không biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Câu 5: Cho hình vuông ABCD, P thuộc cạnh AB. H là chân đường vuông góc hạ từ B đến PC. Phép đồng dạng biến tam giác BHC thành tam giác PHB. Tìm ảnh của B và D

A. P và Q ($Q\in BC$ và $BQ=BP$)

B. C và Q  ($Q\in BC$ và $BQ=BP$)

C. H và Q

D. P và C

Hiển thị đáp án  

Đáp án: A

Câu 6: Các phép biến hình biến đường thẳng thành đường thẳng song song hoặc trùng với nó có thể kể ra là:

A. Phép vị tự.

B. Phép đồng dạng, phép vị tự.

C. Phép đồng dạng, phép dời hình, phép vị tự.

D. Phép dời dình, phép vị tự.

Hiển thị đáp án  

Đáp án: A

Câu 7: Trong mặt phẳng với hệ trục tọa độ Oxy cho $A\left(1;2\right),B\left(–3;1\right).$ Phép vị tự tâm $I\left(2;–1\right)$ tỉ số $k=2$ biến điểm A thành $A\text{'}$ phép đối xứng tâm B biến $A\text{'}$ thành $B\text{'}$. tọa độ điểm $B\text{'}$ là:

A. $\left(0;5\right)$

B. $\left(5;0\right)$

C. $\left(–6;–3\right)$

D. $\left(–3;–6\right)$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Gọi $A^{\text{'}}\left(x;y\right)$ 

Ta có:  $V\left(I;2\right)\left(A\right)=A^{\text{'}}$

$\Rightarrow \overrightarrow{I{A}^{\text{'}}}=2\overrightarrow{IA}$

$\iff \left\{\begin{array}{l}{x}^{\text{'}}-2=2\left(1-2\right)\\ y^{\text{'}}+1=2\left(2+1\right)\end{array}\right.$

$\Rightarrow A^{\text{'}}\left(0;5\right)$

Phép đối xứng tâm B biến $A\text{'}$ thành $B\text{'}$ nên B là trung điểm $A^{\text{'}}{B}^{\text{'}}$

$\Rightarrow B^{\text{'}}\left(-6;-3\right)$ 

Câu 8: Trong mặt phẳng với hệ trục tọa độ Oxy cho $A\left(–2;–3\right), B\left(4;1\right).$ Phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm A thành $A\text{'}$ biến điểm B thành $B\text{'}$.  Khi đó độ dài $A^{\text{'}}{B}^{\text{'}}$ là:

A. $\frac{\sqrt{52}}{2}$

B. $\sqrt{52}$

C. $\frac{\sqrt{50}}{2}$

D. $\sqrt{50}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Chọn B.

Vì phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm A thành $A\text{'}$ , biến điểm B thành $B\text{'}$ nên

$A^{\text{'}}{B}^{\text{'}}=\frac{1}{2}AB$

$=\frac{1}{2}\sqrt{{\left(4+2\right)}^2+{\left(1+3\right)}^2}$

$=\sqrt{52}$ .

Câu 9: Trong măt phẳng Oxy cho đường thẳng d có phương trình $2x-y=0.$ Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng qua trục Oy sẽ biến d thành đường thẳng nào trong các đường thẳng sau?

A. $2x-y=0.$

B. $2x+y=0.$

C. $4x-y=0.$

D. $2x+y-2=0.$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Tâm vị tự O thuộc đường thẳng d nên $d=V_{(O;-2)}\left(d\right)$.

$d^{\text{'}}=D_{Oy}\left(d\right)$ có phương trình là:

$\left\{\begin{array}{c}{x}^{\text{'}}=-x\\ y^{\text{'}}=y\end{array}\right.$

$\iff \left\{\begin{array}{c}x=-x^{\text{'}}\\ y=y^{\text{'}}\end{array}\right..$  

Mà $2x-y=0$

$\iff 2\left(-x^{\text{'}}\right)-y^{\text{'}}=0$

$\iff 2x^{\text{'}}+y^{\text{'}}=0.$

Câu 10: Trong mặt phẳng Oxy cho đường tròn $\left(C\right)$ có phương trình ${\left(x-2\right)}^2+{\left(y-2\right)}^2=4$. Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $k=\frac{1}{2}$ và phép quay tâm O góc ${90}^0$ sẽ biến $\left(C\right)$ thành đường tròn nào trong các đường tròn sau?

A. ${\left(x–2\right)}^2+{\left(y–2\right)}^2=1$

B. ${\left(x–1\right)}^2+{\left(y–1\right)}^2=1$

C. ${\left(x+2\right)}^2+{\left(y–1\right)}^2=1$

D. ${\left(x+1\right)}^2+{\left(y–1\right)}^2=1$

Hiển thị đáp án  

Đáp án: D

Giải thích:

Đường tròn $\left(C\right)$ có tâm $I\left(2;2\right)$ bán kính $R=2$

Qua $V\left(O;\frac{1}{2}\right):\left(C\right)\to \left(C\text{'}\right)$ nên $(C\text{'})$ có tâm $I^{\text{'}}\left(x;y\right)$

 và bán kính $R^{\text{'}}=\frac{1}{2}R=1$ 

Mà :  $\overrightarrow{O{I}^{\text{'}}}=\frac{1}{2}\overrightarrow{OI}$

$\iff \left\{\begin{array}{l}{x}^{\text{'}}=\frac{1}{2}x\\ y^{\text{'}}=\frac{1}{2}y\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$

$\Rightarrow I^{\text{'}}\left(1;1\right)$

Qua $Q(O;{90}^0):(C\text{'})\to (C\text{'}\text{'})$ nên $(C\text{'}\text{'})$ có tâm ${I^{\text{'}}}^{\text{'}}\left(-1;1\right)$ bán kính ${R^{\text{'}}}^{\text{'}}=R^{\text{'}}=1$ (vì góc quay ${90}^0$ ngược chiều kim đồng hồ biến $I^{\text{'}}\left(1;1\right)$ thành ${I^{\text{'}}}^{\text{'}}\left(-1;1\right)$)

Vậy $\left({C^{\text{'}}}^{\text{'}}\right):{\left(x+1\right)}^2+{\left(y–1\right)}^2=1$

Giả sử đường thẳng $d:ax+by+c=0$ ( với $a^2+b^2>0$ )

có véc tơ chỉ phương $\overrightarrow{v}=(a;b)$

Gọi $M(x;y)\in d$,  $I(x_0;y_0)$

$M\text{'}$ là ảnh của M qua $V\left(I;k\right)$ khi đó  

$\overrightarrow{I{M}^{\text{'}}}=k\overrightarrow{IM}$

$\iff \left\{\begin{array}{l}{x}^{\text{'}}=k(x-x_0)\\ y^{\text{'}}=k(y-y_0)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{x^{\text{'}}+k{x}_0}{k}\\ y=\frac{y^{\text{'}}+k{y}_0}{k}\end{array}\right.$

Do $M\in d$ nên $a\frac{x^{\text{'}}+k{x}_0}{k}+b\frac{y^{\text{'}}+k{y}_0}{k}+c=0$

$\iff \frac{a}{k}{x}^{\text{'}}+\frac{b}{k}{y}^{\text{'}}+c+a{x}_0+b{y}_0=0$

Nên phương trình ảnh $d\text{'}$ có véc tơ chỉ phương $\overrightarrow{v^{\text{'}}}=k\left(a;b\right)$

do đó d và $d\text{'}$ song song hoặc trùng nhau.

Chú ý: loại phép dời hình và phép đồng dạng vì phép quay cũng là phép dời hình và đồng dạng.

Câu 11: Cho tam giác ABC và $A\text{'}B\text{'}C\text{'}$ đồng dạng với nhau theo tỉ số k. Chọn câu sai.

A. k là tỉ số hai trung tuyến tương ứng

B. k là tỉ số hai đường cao tương ứng

C. k là tỉ số hai góc tương ứng

D. k là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng

Hiển thị đáp án  

Đáp án: C

Câu 12: Trong măt phẳng Oxy cho điểm $M\left(2;4\right).$ Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $k=\frac{1}{2}$ và phép đối xứng qua trục Oy sẽ biến M thành điểm nào trong các điểm sau?

A. $\left(1;2\right).$

B. $\left(-2;4\right).$

C. $\left(-1;2\right).$

D. $\left(1;-2\right).$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có: $M^{\text{'}}=V_{\left(O,\frac{1}{2}\right)}\left(M\right);M^{\text{'}\text{'}}$

$=D_{Oy}\left(V_{\left(O;\frac{1}{2}\right)}\left(M\right)\right).$

Tọa độ điểm $M^{\text{'}}$ là:

 $\left\{\begin{array}{c}{x}^{\text{'}}=2.\frac{1}{2}+\left(1-\frac{1}{2}\right)0\\ y^{\text{'}}=4.\frac{1}{2}+\left(1-\frac{1}{2}\right)0\end{array}\right.$

$\iff \left\{\begin{array}{c}{x}^{\text{'}}=1\\ y^{\text{'}}=2\end{array}\right..$

Tọa độ điểm $M^{\text{'}\text{'}}$ là:

 $\left\{\begin{array}{c}{x}^{\text{'}}=-x\\ y^{\text{'}}=y\end{array}\right.$

$\iff \left\{\begin{array}{c}{x}^{\text{'}}=-1\\ y^{\text{'}}=2\end{array}\right..$

Câu 13: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn $\left(C\right)$ và $\left(C^{\text{'}}\right)$ có phương trình $x^2+y^2–4y–5=0$ và $x^2+y^2–2x+2y–14=0$. Gọi $\left(C^{\text{'}}\right)$ là ảnh của $\left(C\right)$ qua phép đồng dạng tỉ số k , khi đó giá trị k là:

A. $\frac{4}{3}$

B. $\frac{3}{4}$

C. $\frac{9}{16}$

D. $\frac{16}{9}$

Hiển thị đáp án  

Đáp án: A

Giải thích:

$\left(C\right)$ có tâm $I\left(0;2\right)$ bán kính $R=3$

$\left(C^{\text{'}}\right)$ có tâm $I\left(1;-1\right)$ bán kính $R=4$

Ta có $\left(C^{\text{'}}\right)$ là ảnh của $\left(C\right)$ qua phép đồng dạng tỉ số k thì 

$4=k.3\iff k=\frac{4}{3}$

Câu 14: Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai Elip $\left(E_1\right)$ và $\left(E_2\right)$ lần lượt có phương trình là: $\frac{x^2}{5}+\frac{y^2}{9}=1$ và $\frac{x^2}{9}+\frac{y^2}{5}=1$. Khi đó $\left(E_2\right)$ là ảnh của $\left(E_1\right)$ qua phép đồng dạng tỉ số k bằng:

A. $\frac{5}{9}$

B. $\frac{9}{5}$

C. k = -1

D. k = 1

Hiển thị đáp án  

Đáp án: D

Giải thích:

$\left(E_1\right)$ có trục lớn $B_1{B}_2=3$

$\left(E_2\right)$ có trục lớn $A_1{A}_2=3$

$\left(E_2\right)$ là ảnh của $\left(E_1\right)$ qua phép đồng dạng tỉ số k thì 

$A_1{A}_2=k.B_1{B}_2$

$\iff 3=3k\iff k=1$

Câu 15: Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm $I\left(1;1\right)$ và đường tròn $\left(C\right)$ có tâm I  bán kính bằng 2. Gọi đường tròn $\left(C^{\text{'}}\right)$ là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc $45°$ và phép vị tự tâm O, tỉ số $\sqrt{2}$. Tìm phương trình của đường tròn $\left(C^{\text{'}}\right)$?

A. $x^2+{\left(y-2\right)}^2=8$

B. ${\left(x-2\right)}^2+y^2=8$

C. ${\left(x-1\right)}^2+{\left(y-1\right)}^2=8$

D. $x^2+{\left(y-1\right)}^2=8$

Hiển thị đáp án  

Đáp án: A

Giải thích:

Đường tròn $\left(C\right)$ có tâm $I(1;1)$, bán kính bằng 2 .

Gọi $J(x_J;y_J)$ là ảnh của $I(1;1)$ qua phép quay tâm O góc quay $45°$.

Ta có: $\left\{\begin{array}{l}{x}_J=1.\cos 45°-1.\sin 45°=0\\ y_J=1.\cos 45°+1.\sin 45°=\sqrt{2}\end{array}\right.$.

(công thức này không có trong SGK cơ bản, nếu sử dụng phải chứng minh cho hs)

Phương trình của ảnh của đường tròn qua phép quay trên là:

$x^2+{\left(y-\sqrt{2}\right)}^2=4$.

Gọi $K(x_K;y_K)$ là ảnh của J qua phép vị tự tâm O tỉ số $\sqrt{2}$.

Ta có: $\left\{\begin{array}{l}{x}_K=\sqrt{2}.0=0\\ y_K=\sqrt{2}.\sqrt{2}=2\end{array}\right.$.

Bán kính của đường tròn qua phép vị tự này bằng $2\sqrt{2}$.

Phương trình của ảnh của đường tròn qua phép vị tự trên là $x^2+{\left(y-2\right)}^2=8$.

Câu 16: Trong mặt phẳng Oxy cho đường tròn $\left(C\right):x^2+y^2-6x+4y-23=0,$ tìm phương trình đường tròn $\left(C^{\text{'}}\right)$ là ảnh của đường tròn $\left(C\right)$ qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ $\overrightarrow{v}=\left(3;5\right)$ và phép vị tự $V_{\left(O;-\frac{1}{3}\right)}.$ 

A. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=4.$

B. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=36.$

C. $\left(C\text{'}\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=6.$

D. $\left(C\text{'}\right):{\left(x-2\right)}^2+{\left(y-1\right)}^2=2.$

Hiển thị đáp án  

Đáp án: A

Giải thích:

Đường tròn $\left(C\right)$ có tâm $I\left(3;-2\right)$ và

bán kính $R=\sqrt{9+4+23}=6.$

$I\left(3;-2\right)\underset{\overrightarrow{v}=\left(3;5\right)}{\overset{T_{\overrightarrow{v}}}{\to }}I\text{'}\left(6;3\right)$

$\stackrel{V_{\left(O;-\frac{1}{3}\right)}}{\to }I\text{'}\text{'}\left(-2;-1\right).$.

Vậy $\left(C\right):{\left(x+2\right)}^2+{\left(y+1\right)}^2=4.$ 

Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn: $\left(C\right):x^2+y^2+2x-2y-2=0$, $\left(D\right):x^2+y^2+12x-16y=0$. Nếu có phép đồng dạng biến đường tròn $\left(C\right)$ thành đường tròn $\left(D\right)$ thì tỉ số k của phép đồng dạng đó bằng:

A. 2

B. 3

C. 4

D. 5

Hiển thị đáp án  

Đáp án: D

Giải thích:

+ Phương trình của $\left(C\right):x^2+y^2+2x-2y-2=0$

 có tâm $I\left(-1;1\right)$, bán kính $R=2$. 

+ Phương trình của $\left(D\right):x^2+y^2+12x-16y=0$

$\Rightarrow \left(D\right)$ có tâm $J(-6;8)$, bán kính $r=10$ 

Tỉ số của phép đồng dạng là $k=\frac{r}{R}=5$ 

Câu 18: Trong mặt phẳng với hệ tọa độ Oxy, cho bốn điểm $A\left(-2;1\right),B\left(0;3\right),$$C\left(1;-3\right),$ $D\left(2;4\right)$. Nếu có phép đồng dạng biến đoạn thẳng AB thành đoạn thẳng CD thì tỉ số k của phép đồng dạng đó bằng:

A. 2

B. $\frac{3}{2}$

C. $\frac{5}{2}$

D. $\frac{7}{2}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có: $AB=2\sqrt{2},CD=5\sqrt{2}$. 

Suy ra tỉ số của phép đồng dạng là $k=\frac{CD}{AB}=\frac{5}{2}$.

Câu 19: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm $P\left(3;-1\right)$. Thực hiện liên tiếp hai phép vị tự  $V\left(O;4\right)$ và $V\left(O;-\frac{1}{2}\right)$ điểm P biến thành điểm $P\text{'}$ có tọa độ là:

A. $\left(4;-6\right)$

B. $\left(6;-2\right)$

C. $\left(-6;2\right)$

D. $\left(12;-4\right)$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Giả sử ta có: Phép vị tự $V\left(O;k_1\right)$ biến điểm M thành điểm N

và phép vị tự $V\left(O;k_2\right)$ biến điểm N thành điểm P .

Khi đó ta có: $\overrightarrow{ON}=k_1\overrightarrow{OM}$ và $\overrightarrow{OP}=k\overrightarrow{ON}$.

Suy ra $\overrightarrow{OP}=k_1{k}_2\overrightarrow{OM}$.                  

Như thế P là ảnh của M qua phép vị tự $V\left(O;k_1{k}_2\right)$ 

Áp dụng kết quả trên phép vị tự biến điểm P thành điểm $P\text{'}$ là phép vị tự V tâm I theo tỉ số  

$k=k_1{k}_2=4\left(-\frac{1}{2}\right)=-2$

Ta được:  $\overrightarrow{O{P}^{\text{'}}}=-2\overrightarrow{OP}$

$\Rightarrow \overrightarrow{O{P}^{\text{'}}}=\left(-6;2\right).$

Vậy $P^{\text{'}}\left(-6;2\right)$.

Câu 20: Cho tam giác ABC vuông cân tại A. Nếu có phép đồng dạng biến cạnh AB thành cạnh BC thì tỉ số  của phép đồng dạng đó bằng:

A. 2

B. $\sqrt{2}$

C. $\sqrt{3}$

D.$\frac{\sqrt{2}}{2}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có tam giác ABC vuông cân tại A : $BC=AB\sqrt{2}$ 

Ta dễ thấy tỉ số đồng dạng là $k=\frac{BC}{AB}=\frac{AB\sqrt{2}}{AB}=\sqrt{2}$.

Câu 21: Trong mặt phẳng với hệ trục tọa độ Oxy cho đường thẳng $d:x–2y+1=0$, Phép vị tự tâm $I\left(0;1\right)$ tỉ số $k=–2$ biến đường thẳng d thành đường thẳng $d\text{'}$. phép đối xứng trục Ox biến đường thẳng $d\text{'}$ thành đường thẳng $d_1$. Khi đó phép đồng dạng biến đường thẳng d thành $d_1$ có phương trình là:

A. $2x–y+4=0$

B. $2x+y+4=0$

C. $x–2y+8=0$

D. $x+2y+4=0$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Gọi $M\left(x;y\right)\in d$, $M^{\text{'}}\left(x^{\text{'}};y^{\text{'}}\right)$ là ảnh của M qua $V\left(I;-2\right)$ 

Ta có :  $\overrightarrow{I{M}^{\text{'}}}=-2\overrightarrow{IM}$

$\iff \left\{\begin{array}{l}{x}^{\text{'}}-0=-2\left(x-0\right)\\ y^{\text{'}}-1=-2\left(y-1\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-\frac{x^{\text{'}}}{2}\\ y=-\frac{y^{\text{'}}-3}{2}\end{array}\right.$

$\Rightarrow M\left(-\frac{x^{\text{'}}}{2};-\frac{y^{\text{'}}-3}{2}\right)$

Vì  $M\left(x;y\right)\in d$ nên : 

$-\frac{x^{\text{'}}}{2}–2\left(-\frac{y^{\text{'}}-3}{2}\right)+1=0$

$\iff x^{\text{'}}-2y^{\text{'}}+8=0$

Vậy  $d^{\text{'}}:x-2y+8=0$

Câu 22: Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) tâm $I\left(3;2\right),$ bán kính $R=2$. Gọi $\left(C\text{'}\right)$ là ảnh của $\left(C\right)$ qua phép đồng dạng tỉ số $k=3$. khi đó trong các mệnh đề sau mệnh đề nào sai:

A. $\left(C^{\text{'}}\right)$ có phương trình ${\left(x–3\right)}^2+{\left(y–2\right)}^2=36$

B. $\left(C^{\text{'}}\right)$ có phương trình $x^2+y^2–2y–35=0$

C. $\left(C^{\text{'}}\right)$ có phương trình $x^2+y^2+2x–36=0$

D. $\left(C^{\text{'}}\right)$ có bán kính bằng 6.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có $\left(C^{\text{'}}\right)$ là ảnh của $\left(C\right)$ qua phép đồng dạng tỉ số $k=3$ thì 

$\left(C^{\text{'}}\right)$ có bán kính $R^{\text{'}}=3R=6$  .

Mà phương trình $\left(C^{\text{'}}\right):x^2+y^2+2x–36=0$ có bán kính $R=\sqrt{37}$ nên đáp án C sai.

Câu 23:Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

A. AIFD

B. BCFI

C. CIEB

D. DIEA

Hiển thị đáp án  

Đáp án: C

Giải thích: 

$V_{(C;2)}\left(IGHF\right) = \left(AIFD\right); {Đ}_I\left(AIFD\right) = CIEB.$

Đáp án C.

Câu 24: Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 1/2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.

A. (2;-1)

B. (8;1)

C. (4;-2)

D. (8;4)

Hiển thị đáp án  

Đáp án: A

Giải thích:

Câu 25: Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:

A. P hợp thành bởi phép đối xứng tâm O và phép vị tự tâm A tỉ số k = 2

B. P hợp thành bởi phép đối xứng trục AC và phép vị tự tâm C tỉ số k = 2

C. P hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm O

D. P hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O tỉ số k = -1

Hiển thị đáp án  

Đáp án: D

Giải thích:

Đáp án A:

$$\begin{gathered} {Đ}_O\left(\Delta OCF\right)=\Delta OAE \\ {V}_{\left(A;2\right)}\left(\Delta OAE\right)=\Delta CAB \end{gathered}$$

Đáp án B:

$$\begin{gathered} {Đ}_{AC}\left(\Delta OCF\right)=\Delta OCM \\ {V}_{\left(C;2\right)}\left(\Delta OCM\right)=\Delta ACB \end{gathered}$$

Đáp án C:

$$\begin{gathered} V_{\left(C;2\right)}\left(\Delta OCF\right)=\Delta ACD \\ {Đ}_O\left(\Delta ACD\right)=\Delta CAB \end{gathered}$$

Đáp án D:

$$\begin{gathered} {Đ}_{BD}\left(\Delta OCF\right)=\Delta OAN \\ {V}_{\left(O;-1\right)}\left(\Delta OAN\right)=\Delta OCM \end{gathered}$$

Vậy phép đồng dạng P được hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O, tỉ số k = -1 không biến tam giác OCF thành tam giác CAB.

Câu 26: Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.

A. (8; -3)

B. (-8;3)

C. (-8;-3)

D. (3;8)

Hiển thị đáp án  

Đáp án: A

Giải thích:

Câu 27: Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x - y - 1 = 0 thành đường thẳng d’ có phương trình.

A. x - y + 3 = 0

B. x + y - 3 = 0

C. x + y + 3 = 0

D. x - y + 2 = 0

Hiển thị đáp án  

Đáp án: B

Giải thích:

Phương trình đường thẳng d: x - y - 1= 0

Lấy M(x; y) thuộc d

Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì $\overrightarrow{O{M}^{\text{'}}}=3\overrightarrow{OM}\iff \left\{\begin{array}{l}x\text{'}=3x\\ y\text{'}=3y\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{1}{3}{x}^{\text{'}}\\ y=\frac{1}{3}{y}^{\text{'}}\end{array}\right.$

Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)

$\iff \left\{\begin{array}{l}{x^{\text{'}}}^{\text{'}}=x^{\text{'}}\\ {y^{\text{'}}}^{\text{'}}=-y^{\text{'}}\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{1}{3}{x^{\text{'}}}^{\text{'}}\\ y=-\frac{1}{3}{y^{\text{'}}}^{\text{'}}\end{array}\right.$

Thay vào phương trình d ta được:

Hay x’’ + y’’ - 3 = 0

Vậy phương trình đường thẳng d’: x + y - 3 = 0.

Câu 28: Trong mặt phẳng Oxy, cho điểm M(2;6). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $\mathrm{k}=\frac{1}{2}$ và phép đối xứng qua trục Oy sẽ biến M thành điểm có tọa độ

A. (1,3)

B. (1,-3)

C. (-1,-3)

D. (-1,3)

Hiển thị đáp án  

Đáp án: C

Giải thích:

Phép vị tự tâm O tỉ số k = 1/2 biến điểm M(2;6) thành điểm M’(1; 3). Phép đối xứng qua trục Oy sẽ biến M’(1;3) thành điểm M’’(-1;3).

Câu 29: Trong các phép biến hình có được bằng cách thực hiện liên tiếp hai phép biến hình sau đây, phép không là phép dời hình :

A. Phép đối xứng trục và phép đối xứng tâm.

B. Phép đối xứng tâm và phép vị tự tỉ số k = −1.

C. Phép quay và phép chiếu vuông góc lên một đường thẳng

D. Phép quay và phép tịnh tiến

Hiển thị đáp án  

Đáp án: C

Giải thích: Phép quay và phép chiếu vuông góc lên một đường thẳng

Câu 30: Trong các khẳng định sau, khẳng định nào sai?

A. Thực hiện liên tiếp hai phép đồng dạng thì được một phép đồng dạng.
B. Phép dời hình là phép đồng dạng tỉ số k = 1.
C. Phép vị tự có tính chất bảo toàn khoảng cách.
D. Phép vị tự không là phép dời hình.

Hiển thị đáp án  

Đáp án: C

Câu 31: Phóng to một hình chữ nhật kích thước là 4 và 5 theo phép đồng dạng tỉ số k=3 thì được hình có diện tích là:
A. 60 đơn vị diện tích.

B. 180 đơn vị diện tích.

C. 120 đơn vị diện tích.

D. 20 đơn vị diện tích.

Hiển thị đáp án  

Đáp án: B

Giải thích: Qua phép đồng dạng tỉ số k=3 ta được các cạnh tương ứng của hình chữ nhật là 12 và 15.
Diện tích của hình chữ nhật ảnh là: 12.15 = 180.

Câu 32: Mệnh đề nào sau đây là đúng?
A. Mọi phép đồng dạng đều biến đường thẳng thành đường thẳng song song hoặc trùng với nó
B. Mọi phép đồng dạng biến hình vuông thành hình vuông.
C. Tồn tại phép đồng dạng biến hình chữ nhật (không phải hình vuông) thành hình vuông.
D. Phép đồng dạng biến tam giác thành tam giác có cùng diện tích.

Hiển thị đáp án  

Đáp án: B

Câu 33: Trong các mệnh đề mệnh đề nào sai ?

A. Phép dời là phép đồng dạng tỉ số k=1.

B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

C. Phép vị tự tỉ số k là phép đồng dạng tỉ số open vertical bar k close vertical bar

D. Phép đồng dạng bảo toàn độ lớn góc.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Vì phép quay là phép đồng dạng mà phép quay với góc quay $\alpha \ne k\mathrm{\pi } (\mathrm{k}\in \mathrm{\mathbb{Z}})$ 

thì không biến đường thẳng thành đường thẳng song song hoặc trùng /với nó

Câu 34: Trong mặt phẳng Oxy, cho điểm M(4;8). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $\mathrm{k}=\frac{1}{2}$ và phép đối xứng qua trục Oy sẽ biến M thành điểm có tọa độ

A. (2,4)

B. (2,-4)

C. (-2,-4)

D. (-2,4)

Hiển thị đáp án  

Đáp án: D

Giải thích:

Phép vị tự tâm O tỉ số k = 1/2 biến điểm M(4;8) thành điểm M’(2; 4). Phép đối xứng qua trục Oy sẽ biến M’(2;4) thành điểm M’’(-2;4).

Câu 35:

Trong mặt phẳng với hệ trục tọa độ , cho điểm  và đường tròn  có tâm  bán kính bằng . Gọi đường tròn  là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm , góc  và phép vị tự tâm , tỉ số . Tìm phương trình của đường tròn ?       

A.

B.

C.

D.   

Hiển thị đáp án  

Đáp án: A

Giải thích: Đường tròn  có tâm , bán kính bằng . Gọi  là ảnh của  qua phép quay tâm  góc quay .

Ta có: 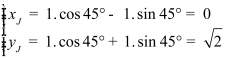. (công thức này không có trong SGK cơ bản) Phương trình của ảnh của đường tròn qua phép quay trên là: . Gọi  là ảnh của  qua phép vị tự tâm  tỉ số . Ta có: 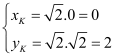. Bán kính của đường tròn qua phép vị tự này bằng .

Phương trình của ảnh của đường tròn qua phép vị tự trên là . 

Câu 36: Phóng to một hình tam giác có chiều cao là 4 và độ dài đáy 6 theo phép đồng dạng tỉ số k=3 thì được hình có diện tích là:
A. 216 đơn vị diện tích.

B. 108 đơn vị diện tích.

C. 36 đơn vị diện tích.

D. 12 đơn vị diện tích.

Hiển thị đáp án  

Đáp án: B

Giải thích: Qua phép đồng dạng tỉ số k=3 ta được các cạnh tương ứng của hình chữ nhật là 12 và 18.
Diện tích của hình chữ nhật ảnh là: 1/2.12.18 = 108.

Câu 37: Cho đường thẳng d: x – y + 1 = 0. Viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I (1; 1), tỉ số k = 2 và phép tịnh tiến theo vectơ  

A. x – y + 3 = 0

B. x – y + 2 = 0 

C. x + y + 3 = 0 

D. x – y – 3 = 0 

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có M(0;1) ∈ d  

Qua phép vị tự tâm I, tỉ số k = 2 ta có: V_(I;2)(d) = d₁ 

Suy ra phương trình d₁ có dạng x – y + c = 0

Mặt khác: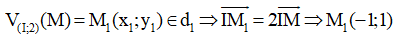  

Vậy d₁: x - y + 2 = 0 

Qua phép tịnh tiến theo vectơ 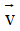 ta có: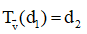  

Suy ra phương trình d₂ có dạng: x – y + d = 0

 

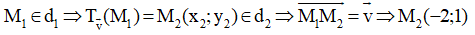
Vậy d₂ có phương trình x – y + 3 = 0

Qua phép đồng dạng đường thẳng d: x – y + 1 = 0 trở thành đường thẳng 

d₂: x – y + 3 = 0 

Câu 38: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai đường thẳng bất kỳ luôn đồng dạng.

B. Hai đường tròn bất kỳ luôn đồng dạng.

C. Hai hình vuông bất kỳ luôn đồng dạng.

D. Hai hình chữ nhật bất kỳ luôn đồng dạng.

Hiển thị đáp án  

Đáp án: D

Giải thích: Với hai hình chữ nhật bất kỳ ta chọn từng cặp cạnh tương ứng khi đó tỉ lệ giữa chúng chưa chắc đã bằng nhau. Vì vậy không phải lúc nào cũng tồn tại phép đồng dạng biến hình chữ nhật này thành hình chữ nhật kia.

Câu 39: Nếu thực hiện liên tiếp phép đồng dạng tỉ số p và phép đồng dạng tỉ số k thì ta được phép đồng dạng có tỉ số

A. p/k

B. p.k

C. p + k

D. p - k

Hiển thị đáp án  

Đáp án: B

Giải thích:

* Thực hiện phép đồng dạng F1, tỉ số p: Biến 2 điểm A; B lần lượt thành 2 điểm A'; B'

suy ra: A'B' = p.AB (1)

* Sau đó, thực hiện phép đồng dạng F2 tỉ số k : biến 2 điểm A'; B' thành 2 điểm A"; B"

suy ra: A"B" = k. A'B' (2)

Từ (1) và (2) suy ra: A"B" = p.k.AB

Do đó, khi thực hiện liên tiếp 2 phép đồng dạng tỉ số k và p thì được phép đồng dạng tỉ số p.k

Câu 40: Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến B thành M, C thành N. Khi đó k bằng

A. 2

B. -2

C. 1/2

D. -1/2

Hiển thị đáp án  

Đáp án: C

Giải thích:

vì $M=V_{\left(A;k\right)}\left(B\right)\Rightarrow \overrightarrow{AM } =k. \overrightarrow{ AB}$

Lại có  $\overrightarrow{AM} = \frac{1}{2}\overrightarrow{ AB\hspace{0.17em}}$ => k = $\frac{1}{2}$

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Bài ôn tập chương 1 có đáp án

Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án 

Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án

Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án 

Trắc nghiệm Hai mặt phẳng song song có đáp án