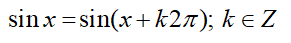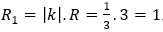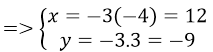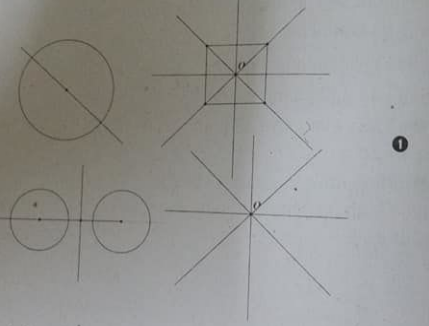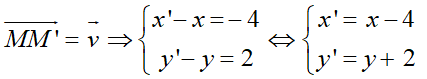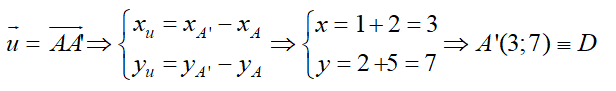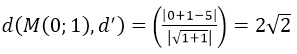TOP 40 câu Trắc nghiệm Bài ôn tập chương 1 (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài ôn tập chương 1 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài Ôn tập chương 1.
Trắc nghiệm Toán 11 Bài: Ôn tập chương 1
Câu 1: Trong một mặt phẳng, với phép biến hình f biến hình H thành hình H’. Khi đó
A. Mỗi hình H’ có ít nhất một hình H mà f(H) = H’
B. Mỗi hình H’ có không quá một hình H mà f(H) = H’
C. Mỗi hình H’ có chỉ một hình H mà f(H) = H’
D. Mỗi hình H’ có không phải một hình H mà f(H) = H’
Đáp án: C
Câu 2: Cho tam giác ABC với G là trọng tâm, trực tâm H và tâm đường tròn ngoại tiếp. Gọi lần lượt là trung điểm các cạnh của tam giác ABC. Hỏi qua phép biến hình nào thì điểm O biến thành điểm H ?
A. Phép vị tự tâm G , tỉ số -2 .
B. Phép quay tâm O , góc quay .
C. Phép tịnh tiến theo vectơ .
D. Phép vị tự tâm G, tỉ số .
Đáp án: A
Giải thích:
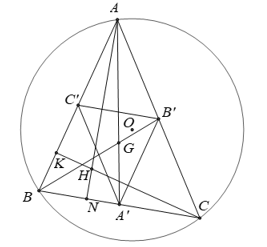
Ta có do đó ta có O chính là trực tâm của tam giác .
Vì phép vị tự tâm G tỉ số -2 biến tam giác thành ABC nên sẽ biến trực tâm tam giác này thành tam giác kia, tức là O biến thành điểm H.
Câu 3: Trong mặt phẳng, với H là một hình (không phải một điểm) và phép biến hình f mà f(H) = H’. Khi đó
A. f(M) = M với mọi điểm M thuộc H
B. f(M) ≠ M với mọi điểm M thuộc H
C. f(M) ≠ M hoặc f(M) = M với điểm M thuộc H
D. f(M) = M với đúng một điểm M thuộc H
Đáp án: C
Câu 4: Trong mặt phẳng,
A. Nếu phép biến hình f biến hình H thành hình H thì f là phép đồng nhất
B. Nếu phép biến hình f biến điểm M thành điểm M thì f là phép đồng nhất
C. Nếu phép biến hình f biến một số điểm M thành chính nó thì f là phép đồng nhất
D. Nếu phép biến hình f biến mọi điểm M thành chính nó thì f là phép đồng nhất
Đáp án: D
Câu 5: Mệnh đề nào sau đây là sai ?
Trong mặt phẳng, có phép biến hình f
A. Biến mọi điểm M thành một điểm M’
B. Biến mọi điểm M thuộc đường thẳng d thành một điểm M’
C. Biến một điểm M thành hai điểm M’ và M’’ phân biệt
D. Biến hai điểm phân biệt M và M’ thành một điểm M’’
Đáp án: C
Câu 6: Cho hai điểm A,B phân biệt. Hãy chọn khẳng định sai trong các khẳng định sau đây:
A. Có duy nhất phép đối xứng trục biến điểm A thành B.
B. Có duy nhất phép đối xứng tâm biến điểm A thành B.
C. Có duy nhất phép tịnh tiến biến điểm A thành B.
D. Có duy nhất phép vị tự biến điểm A thành B.
Đáp án: D
Giải thích:
Có duy nhất phép đối xứng trục d biến điểm A thành B với d là trung trực AB (mỗi đoạn có duy nhất một trung trực)
Có duy nhất phép đối xứng tâm I biến điểm A thành B (AB có duy nhất một trung điểm I)
Có duy nhất phép tịnh tiến biến điểm A thành (vì là duy nhất với A, cố định cho trước)
Phép vị tự do đó ứng với mỗi tâm vị tự I và một tỉ số k cho ta một phép vị tự, do đó có vô số phép vị tự.
Câu 7: Cho hai đường tròn tiếp xúc nhau ở A. Hãy chọn phát biểu sai trong các phát biểu sau:
A. Tiếp điểm A là tâm vị tự trong của hai đường tròn.
B. Tiếp điểm A là một trong hai tâm vị tự trong hoặc ngoài của hai đường tròn.
C. Nếu hai đường tròn đó tiếp xúc ngoài thì tiếp điểm A là tâm vị tự trong.
D. Nếu hai đường tròn đó tiếp xúc trong thì tiếp điểm A là tâm vị tự ngoài.
Đáp án: A
Giải thích:
Nếu hai đường tròn tiếp xúc trong với nhau thì phép vị tự tâm A, tỉ số hoặc biến đường tròn này thành đường tròn kia.
Do đó A chính là tâm vị tự ngoài. (Đáp án D đúng)
Câu 8: Cho hai đường tròn bằng nhau và . Có bao nhiêu phép vị tự biến đường tròn thành ?
A. Vô số.
B. 1 .
C. 2 .
D. Không có.
Đáp án: B
Giải thích:
Chỉ có duy nhất một phép vị tự là phép vị tự có tâm là trung điểm của và tỉ số vị tự bằng -1 .
Câu 9: Tìm mệnh đề sai trong các mệnh đề sau:
A. Có một phép tịnh tiến biến mỗi điểm trong mặt phẳng thành chính nó.
B. Có một phép quay biến mỗi điểm trong mặt phẳng thành chính nó.
C. Có một phép vị tự biến mỗi điểm trong mặt phẳng thành chính nó.
D. Có một phép đối xứng trục biến mỗi điểm trong mặt phẳng thành chính nó.
Đáp án: D
Giải thích:
Chỉ có những điểm trên trục đối xứng mới biến thành chính nó.
Câu 10: Trong một mặt phẳng, với phép biến hình f biến hình H thành hình H’. Khi đó
A. Hình H’ có thể trùng với hình H
B. Hình H’ luôn luôn trùng với hình H
C. Hình H’ luôn là tập con của hình H
D. Hình H luôn là tập con của hình H’
Đáp án: A
Câu 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình và vectơ . Để phép tịnh tiến theo biến đường thẳng d thành chính nó, ta phải chọn m là số:
A. 2.
B. -1.
C. 1.
D. 3.
Đáp án: B
Giải thích:
Biểu thức tọa độ của phép tịnh tiến
hay
Do nên
.
Theo giả thiết ta có
.
Câu 12: Trong mặt phẳng Oxy, cho đường thẳng và điểm . Phép đối xứng tâm I biến đường thẳng d thành đường thẳng có phương trình:
A. .
B.
C. .
D. .
Đáp án: A
Giải thích:
Biểu thức tọa độ của phép đối xứng tâm là
Ta có
nên
Do đó
hay
Câu 13: Giả sử là hình gồm hai đường thẳng song song, là hình bát giác đều. Khi đó:
A. không có trục đối xứng, không có tâm đối xứng; có 8 trục đối xứng.
B. có vô số trục đối xứng, vô số có tâm đối xứng; có 8 trục đối xứng.
C. chỉ có một có trục đối xứng, không có tâm đối xứng; có 8 trục đối xứng.
D. có vô số trục đối xứng, chỉ có một tâm đối xứng; có 8 trục đối xứng.
Đáp án: B
Giải thích:
(H1)
(H2)
Hai đường thẳng song song và có vô số trục đối xứng (là các đề , và các đường thẳng vuông góc , )
Hai đường thẳng song song và có vô số tâm đối xứng là các điểm nằm trên
có 8 trục đối xứng là 4 đường chéo chính (đường chéo đi qua tâm) và 4 đường trung trực (trung trực của hai cạnh đối diện).
Câu 14: Thực hiện liên tiếp một phép đối xứng tâm và một phép tịnh tiến ta được:
A. Phép quay.
B. Phép đối xứng trục.
C. Phép đối xứng tâm.
D. Phép tịnh tiến.
Đáp án: C
Giải thích:
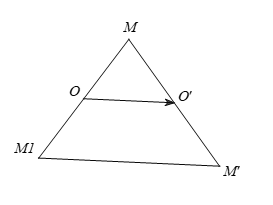
Gọi là ảnh của M qua phép đối xứng tâm O. là ảnh của qua phép tịnh tiến theo .
Gọi là trung điểm của thì .
Vậy điểm hoàn toàn xác định nên phép biến hình biến điểm M thành là phép đối xứng tâm.
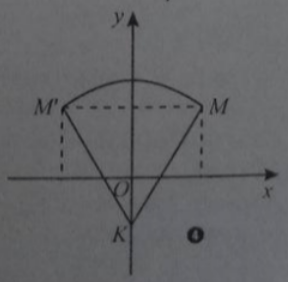
Câu 15: Cho hình gồm hai đường tròn và có bán kính bằng nhau và cắt nhau tại hai điểm. Trong những nhận xét sau, nhận xét nào đúng?
A. có hai trục đối xứng nhưng không có tâm đối xứng.
B. có một trục đối xứng.
C. có hai tâm đối xứng và một trục đối xứng.
D. có một tâm đối xứng và hai trục đối xứng.
Đáp án: D
Giải thích:
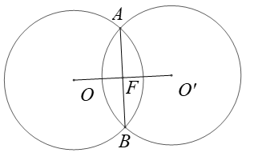
Hai trục đối xứng là đường thẳng và AB.
Tâm đối xứng chính là giao của hai trục đối xứng, tức là điểm K.
Câu 16: Trong mặt phẳng với hệ trục tọa độ Oxy. Cho phép đối xứng trục Oy, phép đối xứng trục Oy biến parabol thành parabol có phương trình là:
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
Biểu thức tọa độ của phép đối xứng trục Oy là .
Do
Câu 17: Trong các mệnh đề sau đây mệnh đề nào sai?
A. Các hình HE, SHE, IS có một trục đối xứng
B. Các hình: CHAM, HOC, THI, GIOI không có trục đối xứng.
C. Các hình: SOS, COC, BIB có hai trục đối xứng
D. Có ít nhất một trong ba mệnh đề a,b,c sai.
Đáp án: A
Giải thích:
Rõ ràng chữ S không có trục đối xứng nên đáp án A sai
Câu 18: Trong mặt phẳng với hệ trục tọa độ Oxy. Phép tịnh tiến theo biến parabol (P): thành parabol (P): có phương trình là:
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
Biểu thức tọa độ của phép tịnh tiến là .
Do nên
.
Câu 19: Cho hai điểm O và phân biệt. Biết rằng phép đối xứng tâm O biến điểm M thành . Phép biến hình biến M thành , phép đối xứng tâm biến điểm thành . Phép biến hình biến M thành là phép gì?
A. Phép quay.
B. Phép vị tự.
C. Phép đối xứng tâm.
D. Phép tịnh tiến.
Đáp án: D
Giải thích:
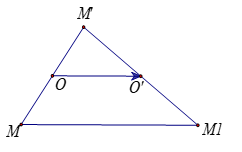
Theo hình vẽ ta có nên phép tịnh tiến theo biến M thành (các điểm thẳng hàng cũng tương tự)
Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến.
B. Thực hiện liên tiếp hai phép đối xứng trục sẽ được một phép đối xứng trục.
C. Thực hiện liên tiếp hai phép đối xứng tâm sẽ được một phép đối xứng tâm.
D. Thực hiện liên tiếp hai phép quay sẽ được một phép quay.
Đáp án: A
Giải thích:
Thực hiện liên tiếp hai phép tịnh tiến sẽ được một phép tịnh tiến trong đó vec tơ tịnh tiến bằng tổng của 2 vec tơ tịnh tiến của hai phép đã cho.
Câu 21: Hai đường thẳng và song song với nhau. Có bao nhiêu phép tịnh tiến biến đường thằng thành đường thẳng ?
A. Vô số.
B. 1.
C. 2.
D. 3.
Đáp án: A
Giải thích:
Nếu vectơ tịnh tiến không phải là VTCP của đường thẳng thì sẽ có vô sô phép tịnh tiến biến đường thẳng thành .
Câu 22: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm . Phép tịnh tiến theo vectơ biến điểm A thành điểm nào trong các điểm sau đây?
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
Theo biểu thức tọa độ :
là tọa độ ảnh.
Câu 23: Trong mặt phẳng với hệ tọa độ, cho điểm . Hỏi A là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo vectơ ?
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Theo biểu thức tọa độ:
là tọa độ của E.
Câu 24: Trong các mệnh đề sau, mệnh đề nào sai?
A. Phép dời hình là một phép đồng dạng.
B. Phép vị tự là một phép đồng dạng.
C. Phép quay là một phép đồng dạng.
D. Phép đồng dạng là một phép dời hình.
Đáp án: D
Giải thích:
Phép dời hình là một phép đồng dạng với tỉ số đồng dạng bằng 1, điều ngược lại không đúng.
Câu 25: Trong mặt phẳng với hệ trục tọa độ Oxy, phép tịnh tiến theo biến điểm thành điểm có tọa độ là:
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Biểu thức tọa độ của phép tịnh tiến là
nên
Câu 26: Trong mặt phẳng Oxy, cho . Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ biến điểm M thành điểm nào trong các điểm sau đây:
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
+ Phép đối xứng tâm O biến điểm thành điểm .
+ Phép tịnh tiến theo vectơ biến điểm thành điểm .
Câu 27: Trong mặt phẳng Oxy. Cho đường tròn . Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ biến đường tròn thành đường tròn nào trong các phương trình sau đây:
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
+ có tâm bán kính .
+ Phép đối xứng qua trục Oy biến thành .
+ Phép tịnh tiến theo vectơ biến thành .
Vậy ảnh của qua phép dời hình đã cho là đường tròn: .
Câu 28: Trong mặt phẳng Oxy, cho đường thẳng . Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ biến đường thẳng thành đường thẳng nào trong các đường thẳng sau đây:
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
+ Phép đối xứng tâm O biến đường thẳng thành .
+ Phép tịnh tiến theo vectơ biến đường thẳng thành đường thẳng .
Câu 29: Trong các mệnh đề sau mệnh đề nào đúng?
A. Thực hiện liên tiếp 2 phép tịnh tiến ta được một phép tịnh tiến.
B. Thực hiện liên tiếp 2 phép đối xứng trục ta được một phép đối xứng trục.
C. Thực hiện liên tiếp phép đối xứng qua tâm và phép đối xứng trục sẽ được một phép đối xứng qua tâm.
D. Thực hiện liên tiếp phép quay và phép tịnh tiến sẽ được một phép tịnh tiến.
Đáp án: A
Giải thích:
+ Thực hiện liên tiếp phép tịnh tiến theo vec-tơ và phép tịnh tiến theo vec-tơ ta được phép tịnh tiến theo vec-tơ .
Câu 30: Trong mặt phẳng Oxy. Cho đường thẳng . Phép vị tự tâm O tỉ số k = -2 biến đường thẳng thành có phương trình là:
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
+ Giả sử qua phép vị tự tâm O tỉ số k = 2 điểm thuộc thành điểm .
+ Thay biểu thức tọa độ của phép vị tự tâm O tỉ số k = -2 ta được:
.
+ Do thuộc nên ta có: .
Vậy phép vị tự tâm O tỉ số k = -2 biến đường thẳng thành có phương trình
là: .
Câu 31: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y – 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (-1; -1) tỉ số 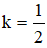 và phép quay tâm O góc -45 độ
và phép quay tâm O góc -45 độ
A. x = 0
B. y = 0
C. x +y = 0
D. x - y = 0
Đáp án: A
Giải thích:
Gọi là ảnh của d qua phép vị tự tâm I (-1; -1) tỉ số 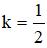 . Vì song song hoặc trùng với d nên phương trình của nó có dạng x + y + c = 0
. Vì song song hoặc trùng với d nên phương trình của nó có dạng x + y + c = 0
Lấy M(1;1) ∈ d
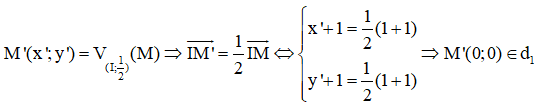
Vậy phương trình của d1: x + y = 0
Ảnh của d1 qua phép quay tâm O góc -45 độ là đường thẳng Oy.
Vậy phương trình d': x = 0
Câu 32: Trong mặt phẳng tọa độ, cho đồ thị của hàm số y = sinx. Có bao nhiêu phép tịnh tiến biến đồ thị đó thành chính nó?
A. Không
B. Một
C. Hai
D. Vô số
Đáp án: D
Giải thích:
Ta biết rằng:
Do đó, nếu ta tịnh tiến đồ thị theo vecto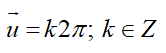
Câu 33. Trong mặt phẳngOxy cho đường tròn (C) có phương trình (x - 1)2 + (y - 2)2 = 4. Phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. (x - 2)2 + (y - 4)2 = 16.
B. (x - 4)2 + (y - 2)2 = 4.
C. (x - 4)2 + (y - 2)2 = 16.
D. (x + 2)2 + (y + 4)2 = 16.
Đáp án: D
Giải thích:
Đường tròn (C) có tâm I(1;2) và bán kính r = 2.
Đường tròn cần tìm có tâm I' = V(O,k)(I) và bán kính r' = |k|.r.
Khi đó: I'(-2;-4) và r' = 4.
Câu 34. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 2)2 + (y + 1)2 = 9. Gọi (C')là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số 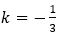

A. R' = 9.
B. R' = 3.
C. R' = 27.
D. R' = 1.
Đáp án: D
Giải thích:
Đường tròn (C) có bán kính R = 3.
Qua phép vị tự tâm O, tỉ số 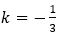
Qua phép tính tiến theo vectơ 
Vậy R' của đường tròn (C') là R' = 1.
Câu 35. Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ
A. M'(-12; -9)
B. M'(12; 9)
C. M'(-9; 12)
D. M'(12; -9)
Đáp án: A
Giải thích:
vecto OM' = vecto -3OM
⇒ M'(12; -9)
Câu 36. Trong mặt phẳng Oxy phép quay tâm K, góc 600 biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
A. (0;0)
B. (0;-√3)
C. (0;1-√3)
D. (√2;0)
Đáp án: C
Giải thích:
Tam giác đều KMM’ có cạnh MM’ = 2 nên đường cao bằng √3.
Suy ra OK = √3-1 ⇒ K(0; 1-√3)
Nhận xét. Phép quay có góc quay bằng ±600 thì tam giác tạo bởi tâm quay, điểm M và ảnh M’ của nó luôn tạo thành một tam giác đều.
Câu 37. Trong các mệnh đề sau mệnh đề nào đúng?
A. Đường tròn là hình có vô số trục đối xứng
B. Hình vuông là hình có vô số trục đối xứng
C. Một hình có hai đường tròn cùng bán kính thì có vô số trục đối xứng
D. Một hình gồm hai đường thẳng vuông góc thì có vô số trục đối xứng
Đáp án: A
Giải thích:
Đường tròn là hình có vô số trục đối xứng: đường thẳng bất kì đi qua tâm.
- Hình vuông có 4 trục đối xứng: Hai đường chéo và hai đường qua trung điểm các cặp cạnh đối diện.
- Hình có hai đường tròn cùng bán kính có 2 trục đối xứng: đường thẳng qua hai tâm và đường trung trực của đoạn thẳng nối hai tâm (hình 1)
Câu 38. Cho vecto v(-4;2) và đường thẳng ∆': 2x - y - 5 = 0. Hỏi ∆' là ảnh của đường thẳng ∆ nào qua Tvecto v:
A. ∆:2x - y - 13 = 0
B. ∆:x - 2y - 9 = 0
C. ∆:2x + y - 15 = 0
D. ∆:2x - y + 15 = 0
Đáp án: D
Giải thích:
Tịnh tiến theo biến điểm M(x;y) thuộc d thành M’(x’;y’) thuộc d’:
Ta có:
Vì M’ thuộc ∆’ nên: 2( x – 4) – (y+ 2) - 5= 0
Hay 2x – y – 15 = 0
Câu 39. Trong mặt phẳng Oxy cho điểm A(2;5). Phép tịnh tiến theo vecto vecto u(1;2) biến A thành điểm nào trong các điểm sau?
A. B(3;1)
B. C(1;6)
C. D(3;7)
D. E(4;7)
Đáp án: C
Giải thích:
Sử dụng biểu thức tọa độ của phép tịnh tiến.
Tịnh tiến theo vecto u(1; 2) biến điểm A(2; 5) thành A’ (x; y), khi đó:
Câu 40. Cho hai đường thẳng d: x + y - 1 = 0 và d’: x + y - 5 = 0. Phép tịnh tiến theo vecto u biến đường thẳng d thành d’. khi đó, độ dài bé nhất của vecto u là bao nhiêu?
A. 5
B. 4√2
C. 2√2
D. √2
Đáp án: C
Giải thích:
Độ dài bé nhất của vecto u bằng khoảng cách từ một điểm bất kì trên d tới d’ bằng :
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án
Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án
Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án
Trắc nghiệm Hai mặt phẳng song song có đáp án
Trắc nghiệm Phép chiếu song song. hình biểu diễn của một hình không gian có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án