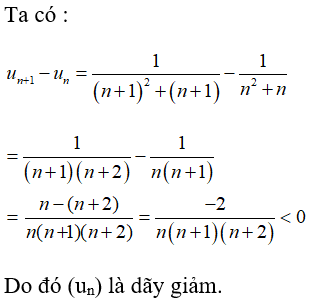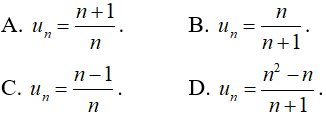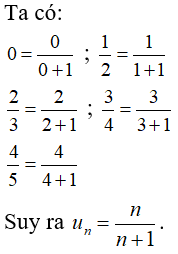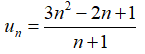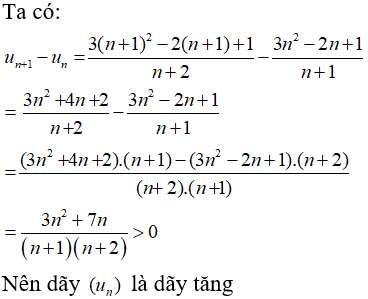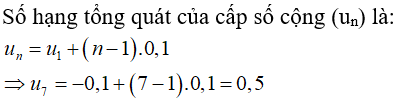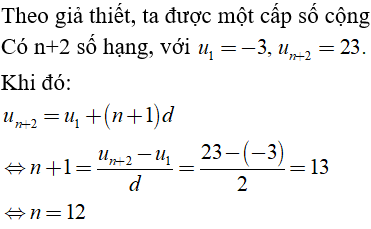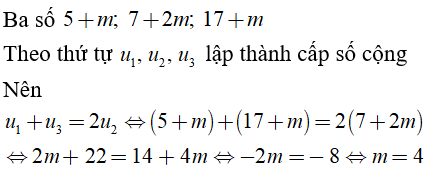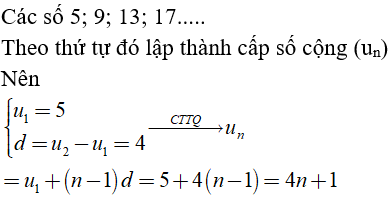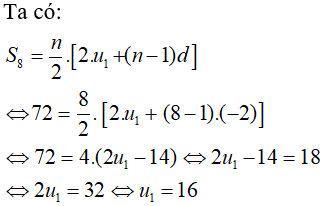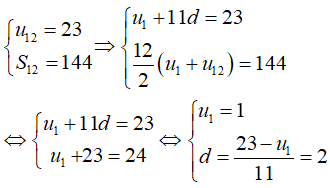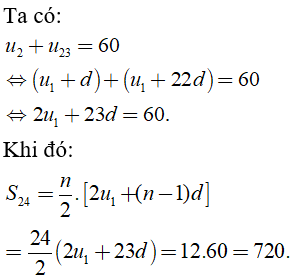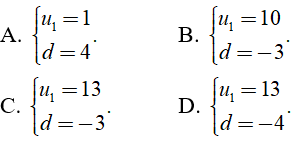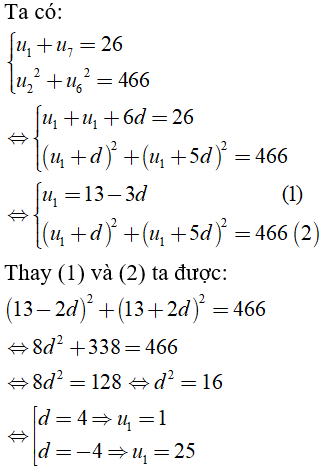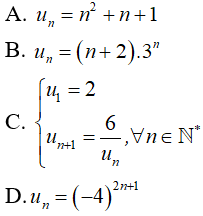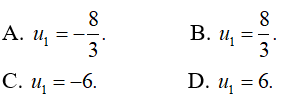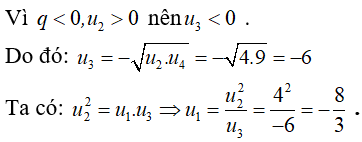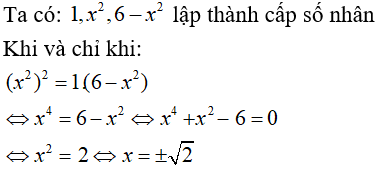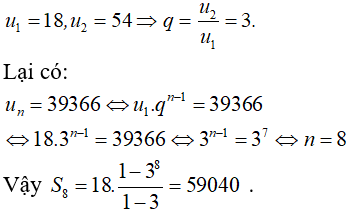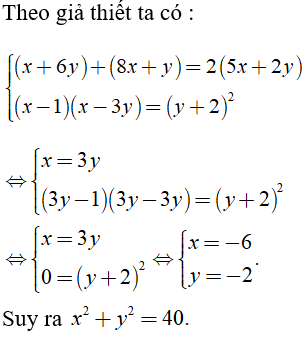TOP 40 câu Trắc nghiệm Dãy số (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 2: Dãy số có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 2.
Trắc nghiệm Toán 11 Bài 2: Dãy số
Bài giảng Trắc nghiệm Toán 11 Bài 2: Dãy số
Câu 1: Cho dãy số có 4 số hạng đầu là: −1,3,19,53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.
A. u10=97
B. u10=71
C. u10=1414
D. u10=971
Đáp án: A
Giải thích:
Xét dãy (un) có dạng: un=an3+bn2+cn+d
Ta có hệ: {a+b+c+d=−18a+4b+2c+d=327a+9b+3c+d=1964a+16b+4c+d=53
Giải hệ trên ta tìm được: a=1,b=0,c=−3,d=1
⇒un=n3−3n+1 là một quy luật.
Số hạng thứ 10: u10=971.
Câu 2: Cho dãy số (un)với un=an2n+1 (a: hằng số). un+1 là số hạng nào sau đây?
A. un+1=a.(n+1)2n+2.
B. un+1=a.(n+1)2n+1.
C. un+1=a.n2+1n+1.
D. un+1=an2n+2.
Đáp án: A
Giải thích:
Ta có
un+1=a.(n+1)2(n+1)+1=a(n+1)2(n+2)2
Câu 3: Cho dãy số có các số hạng đầu là: 5;10;15;20;25;...Số hạng tổng quát của dãy số này là:
A. un=5(n−1).
B. un=5n.
C. un=5+n.
D. un=5.n+1.
Đáp án: B
Giải thích:
Ta có:
5=5.1
10=5.2
15=5.3
20=5.4
25=5.5
Suy ra số hạng tổng quát un=5n.
Câu 4: Cho dãy số có các số hạng đầu là:8,15,22,29,36,....Số hạng tổng quát của dãy số này là:
A. un=7n+7
B. un=7.n
C. un=7.n+1
D. un : Không viết được dưới dạng công thức
Đáp án: C
Giải thích:
Ta có:
8=7.1+1
15=7.2+1
22=7.3+1
29=7.4+1
36=7.5+1
Suy ra số hạng tổng quát un=7n+1.
Câu 5: Cho dãy số có các số hạng đầu là: 0;12;23;34;45;.... Số hạng tổng quát của dãy số này là:
A. un=n+1n
B. un=nn+1
C. un=n−1n
D. un=n2−nn+1
Đáp án: B
Giải thích:
Ta có:
0=00+1
12=11+1
23=22+1
34=33+1
45=44+1
Suy ra un=nn+1.
Câu 6: Cho dãy số có các số hạng đầu là: −2;0;2;4;6;.... Số hạng tổng quát của dãy số này có dạng?
A. un=−2n
B. un=(−2)+n
C. un=(−2)(n+1)
D. un=(−2)+2(n−1)
Đáp án: D
Giải thích:
Dãy số là dãy số cách đều có khoảng cách là 2 và số hạng đầu tiên là (-2) nên un=(−2)+2.(n−1).
Câu 7: Xét tính tăng, giảm và bị chặn của dãy số (un), biết: un=2n−133n−2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Ta có:
un+1−un=2n−113n+1−2n−133n−2
=34(3n+1)(3n−2)>0 với mọi n≥1.
Suy ra un+1>un ∀n≥1⇒ dãy (un) là dãy tăng.
Mặt khác: un=23−353(3n−2)
⇒−11≤un<23 ∀n≥1
Vậy dãy (un) là dãy bị chặn.
Câu 8: Cho dãy số được xác định như sau: {u1=1un=3un−1+12un−1−2, n≥2.
Viết 4 số hạng đầu của dãy và chứng minh rằng un>0, ∀n
A. u1=1,u2=32,u3=476,u4=22734
B. u1=1,u2=32,u3=176,u4=22734
C. u1=1,u2=32,u3=196,u4=22734
D. u1=1,u2=32,u3=176,u4=212734
Đáp án: B
Giải thích:
Ta có: u1=1,u2=32,u3=176,u4=22734.
Ta chứng minh un>0, ∀n bằng quy nạp.
Giả sử un>0, khi đó:
2un+12un≥2√2un.12un=2
Nên un+1
=un+(2un+12un−2)>un>0.
Câu 9: Cho dãy số có các số hạng đầu là: 13;132;133;134;135;…. Số hạng tổng quát của dãy số này là?
A. un=1313n+1
B. un=13n+1
C. un=13n
D. un=13n−1
Đáp án: C
Giải thích:
5 số hạng đầu là 131;132;133;134;135;... nên un=13n.
Câu 10: Cho dãy số (un) với {u1=5un+1=un+n. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=(n−1)n2
B. un=5+(n−1)n2
C. un=5+(n+1)n2
D. un=5+(n+1)(n+2)2
Đáp án: B
Giải thích:
Ta có
un=5+1+2+3+...+n−1
=5+n(n−1)2.
Câu 11: Cho dãy số (un) với {u1=1un+1=un+(−1)2n. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=1+n
B. un=1−n
C. un=1+(−1)2n
D. un=n
Đáp án: D
Giải thích:
Ta có:
un+1=un+(−1)2n=un+1
⇒u2=2;u3=3;u4=4;... Dễ dàng dự đoán được un=n.
Thật vậy, ta chứng minh được un=n (*) bằng phương pháp quy nạp như sau:
+ Với n=1⇒u1=1. Vậy (*) đúng với n=1
+ Giả sử (*) đúng với mọi n=k(k∈ℕ*), ta có: uk=k. Ta đi chứng minh (*) cũng đúng với n=k+1, tức là: uk+1=k+1
+ Thật vậy, từ hệ thức xác định dãy số (un) ta có:
uk+1=uk+(−1)2k=k+1.
Vậy (*) đúng với mọi n∈ℕ*.
Câu 12: Cho dãy số (un) với {u1=1un+1=un+(−1)2n+1. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=2−n.
B. un không xác định.
C. un=1−n.
D. un=−n với mọi n.
Đáp án: A
Giải thích:
Ta có: u2=0;u3=−1;u4=−2,.. Dễ dàng dự đoán được un=2−n .
Câu 13: Xét tính tăng giảm của các dãy số sau: un=3n2−2n+1n+1
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Ta có:
un+1−un=5n2+10n+2(n+1)(n+2)>0
nên dãy (un) là dãy tăng
Câu 14: Xét tính tăng giảm của các dãy số sau: un=n−√n2−1
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: B
Giải thích:
Ta có:
un+1−un
=1(n+1)+√(n+1)2−1−1n+√n2−1<0
Nên dãy (un) giảm.
Câu 15: Cho dãy số (un) với {u1=1un+1=un+n2. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=1+n(n+1)(2n+1)6
B. un=1+n(n−1)(2n+2)6
C. un=1+n(n−1)(2n−1)6
D. un=1+n(n+1)(2n−2)6
Đáp án: C
Giải thích:
Ta có:
{u1=1u2=u1+12u3=u2+22...un=un−1+(n−1)2 .
Cộng hai vế ta được
un=1+12+22+...+(n−1)2
=1+n(n−1)(2n−1)6
Câu 16: Cho dãy số (un) với {u1=2un+1−un=2n−1. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?
A. un=2+(n−1)2.
B. un=2+n2.
C. un=2+(n+1)2.
D. un=2−(n−1)2.
Đáp án: A
Giải thích:
Ta có:
{u1=2u2=u1+1u3=u2+3...un=un−1+2n−3.
Cộng hai vế ta được
un=2+1+3+5+...+(2n−3)
=2+(n−1)2
Câu 17: Cho dãy số (un) với {u1=−2un+1=−2−1un. Công thức số hạng tổng quát của dãy số này là:
A. un=−n−1n
B. un=n+1n
C. un=−n+1n
D. un=−nn+1
Đáp án: C
Giải thích:
Ta có:
u1=−32; u2=−43; u3=−54;...
Dễ dàng dự đoán được un=−n+1n.
Câu 18: Cho dãy số (un) với {u1=12un+1=un−2. Công thức số hạng tổng quát của dãy số này là:
A. un=12+2(n−1).
B. un=12−2(n−1).
C. un=12−2n.
D. un=12+2n.
Đáp án: B
Giải thích:
Ta có:
{u1=12u2=u1−2u3=u2−2...un=un−1−2.
Cộng hai vế ta được
un=12−2−2...−2
=12−2(n−1).
Câu 19: Xét tính tăng giảm của các dãy số sau: un=3n−12n
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Ta có:
un+1−un=un+1−un
=3n+12n+1>0⇒dãy (un) tăng.
Câu 20: Xét tính tăng giảm của các dãy số sau: un=n+(−1)nn2
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: C
Giải thích:
Ta có:
u1=0;u2=12;u3=29
⇒{u2>u1u3<u2⇒Dãy số không tăng không giảm.
Câu 21: Cho dãy số (un) được xác định bởi : {u0=2011un+1=u2nun+1, ∀n=1,2,...
Khẳng định nào sau đây đúng
A. Dãy (un) là dãy giảm
B. Dãy (un) là dãy tăng
C. Dãy (un) là dãy không tăng, không giảm
D. A, B, C đều sai
Đáp án: A
Giải thích:
Ta có:
un+1−un=−unun+1<0, ∀n nên dãy (un) là dãy giảm
Câu 22: Cho dãy số (un) với 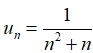
A. Năm số hạng đầu của dãy là: 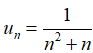
B. Là dãy số tăng.
C. Bị chặn trên bởi số M = 1/2.
D. Không bị chặn.
Đáp án: B
Giải thích:
Câu 23: Cho dãy số có các số hạng đầu là: 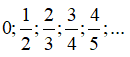
Đáp án: B
Giải thích:
Câu 24: Xét tính tăng giảm của các dãy số sau:
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Cả A, B, C đều sai
Đáp án: A
Giải thích:
Câu 25: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
A. 1, 6
B. 6
C. 0,5
D. 0,6
Đáp án: C
Giải thích:
Câu 26: Cho cấp số cộng (un) thỏa mãn: 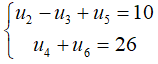
A. d = 2
B. d = 4
C. d = 3
D. d = 5
Đáp án: C
Giải thích:
Câu 27: Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d = 2. Tìm n?
A. n = 12
B. n = 13
C. n = 14
D. n = 15
Đáp án: A
Giải thích:
Câu 28 : Nếu các số 5 + m; 7 + 2m; 17 + m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
A. m = 2
B. m = 3
C. m = 4
D. m = 5
Đáp án: C
Giải thích:
Câu 29: Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng.
A. un = 5n + 1
B. un = 5n - 1
C. un = 4n + 1
D. un = 4n - 1
Đáp án: C
Giải thích:
Câu 30: Cho cấp số cộng (un) có d = -2 và S8 = 72. Tìm số hạng đầu tiên u1?
A. 16
B. –16
C. 4
D. 8
Đáp án: A
Giải thích:
Câu 31: Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu?
A. d = 2
B. d = 3
C. d = 4
D. d = 5
Đáp án: A
Giải thích:
Câu 32: Cho cấp số cộng (un) thỏa mãn u2 + u23 = 60. Tính tổng S24 của 24 số hạng đầu tiên của cấp số cộng đã cho.
A. 60
B. 120
C. 720
D. 1440
Đáp án: C
Giải thích:
Câu 33: Cho cấp số cộng (un) thỏa mãn 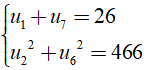
Đáp án: A
Giải thích:
Câu 34: Trong các dãy số (un) sau, dãy nào là cấp số nhân?
Đáp án: D
Giải thích:
Câu 35: Cho cấp số nhân (un) với công bội q < 0 và u2 = 4, u4 = 9. Tìm u1 .
Đáp án: A
Giải thích:
Câu 36: Cho cấp số nhân (un) biết u1 + u5 = 51; u2 + u6 = 102. Hỏi số 12288 là số hạng thứ mấy của cấp số nhân (un) ?
A. Số hạng thứ 10.
B. Số hạng thứ 11.
C. Số hạng thứ 12.
D. Số hạng thứ 13.
Đáp án: D
Giải thích:
Câu 37: Tìm x biết 1, x2, 6 - x2 lập thành cấp số nhân.
A. x = ± 1
B. x = ± 1
C. x = ± √2
D. x = ± √3
Đáp án: B
Giải thích:
Câu 38: Tính tổng tất cả các số hạng của một cấp số nhân , biết số hạng đầu bằng 18, số hạng thứ hai bằng 54 và số hạng cuối bằng 39366.
A. 19674.
B. 59040.
C. 177138.
D. 6552
Đáp án: B
Giải thích:
Câu 39: Các số x + 6y ; 5x + 2y; 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x- 1 ; y + 2 ; x – 3y theo thứ tự đó lập thành một cấp số nhân. Tính x2 + y2
A. 40
B. 25
C. 100
D. 10
Đáp án: A
Giải thích:
Câu 40: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
Đáp án: D
Giải thích:
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+103=1408
trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Cấp số cộng có đáp án
Trắc nghiệm Cấp số nhân có đáp án
Trắc nghiệm Bài ôn tập chương 3 có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án