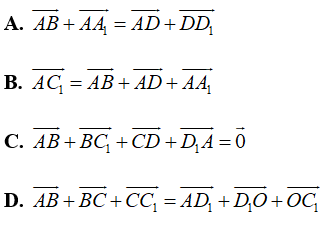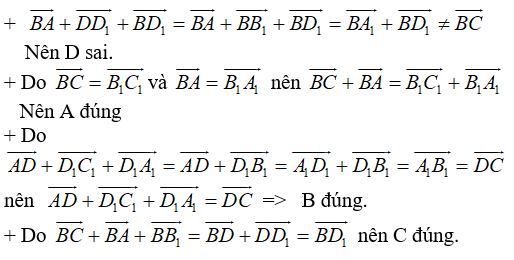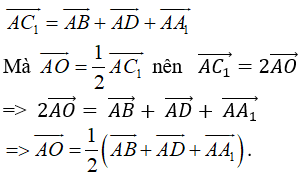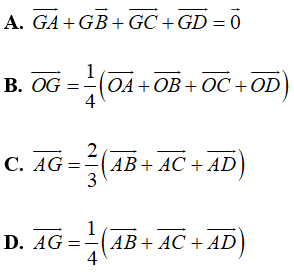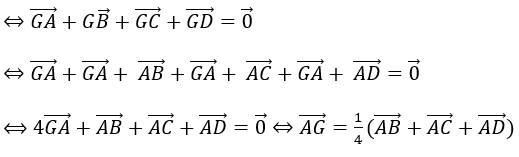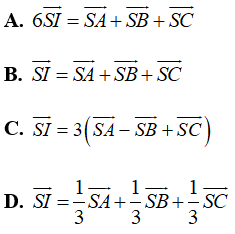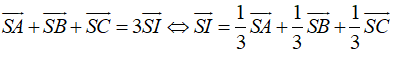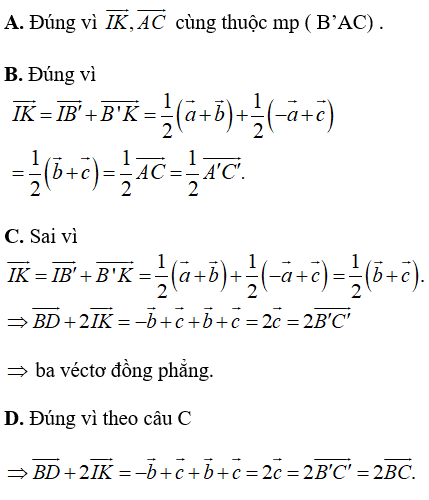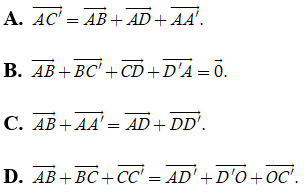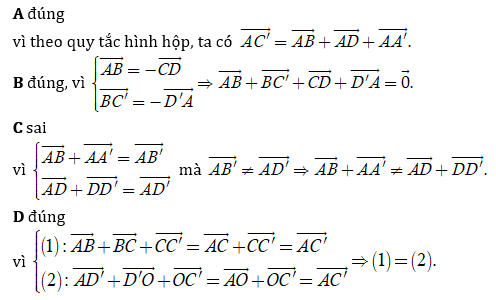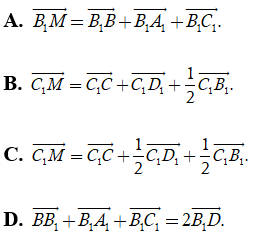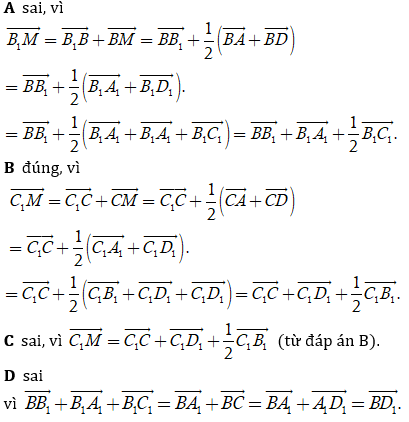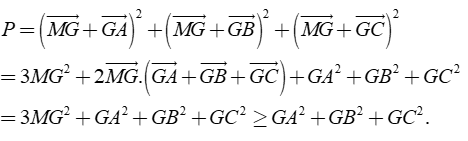TOP 40 câu Trắc nghiệm Vectơ trong không gian (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 1: Vectơ trong không gian có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 1.
Trắc nghiệm Toán 11 Bài 1: Vectơ trong không gian
Câu 1: Cho hình hộp ABCD.A'B'C'D'. Một đường thẳng ∆ cắt các đường thẳng AA',BC,C'D' lần lượt tại M,N,P sao cho →NM=2→NP. Tính MAMA'.
A. MAMA'=1
B. MAMA'=√2
C. MAMA'=2
D. MAMA'=√3
Đáp án: C
Giải thích:
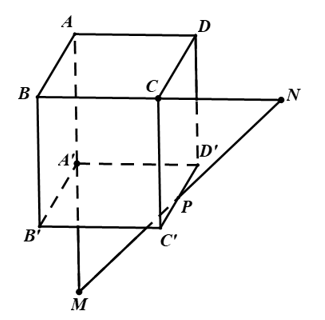
Đặt →AD=→a,→AB=→b,→AA'=→c.
Vì M∈AA' nên →AM=k→AA'=k→c
N∈BC⇒→BN=l→BC=l→a,
P∈C'D'⇒→C'P=m→b
Ta có →NM=→NB+→BA+→AM
=−l→a−→b+k→c
→NP=→BN+→BB'+→B'C'+→C'P
=(1−l)→a+m→b+→c
Do →NM=2→NP
⇒−l→a−→b+k→c
=2[(1−l)→a+m→b+→c]
⇔{−l=2(1−l)−1=2mk=2
⇔k=2,m=−12,l=2.
Vậy MAMA'=2.
Câu 2: Giả sử M, N, P là ba điểm lần lượt nằm trên ba cạnh SA, SB, SC cỏ tứ diện SABC. Gọi I là giao điểm của ba mặt phẳng (BCM), (CAN), (ABP) và J là giao điểm của ba mặt phẳng (ANP), (BPM), (CMN).
Ta được S, I, J thẳng hàng tính đẳng thức nào sau đây đúng?
A. MSMA+NSNB+PSPC+12=JSJI
B. MSMA+NSNB+PSPC+14=JSJI
C. MSMA+NSNB+PSPC+13=JSJI
D. MSMA+NSNB+PSPC+1=JSJI
Đáp án: D
Giải thích:
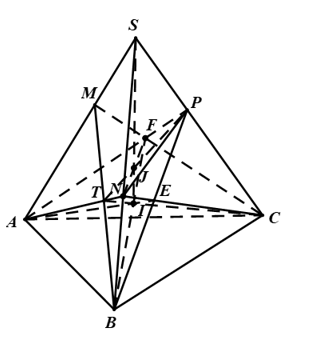
Goi E=BP∩CN,F=CM∩AP,T=AN∩BM.
Trong (BCM) có I=BF∩CT trong (ANP) có NF∩PT=J.
Đặt →SA=→a,→SB=→b,→SC=→c
và →SM=x→MA,→SN=y→NB,→Sp=z→PC
Ta có
→SM=xx+1→a,→SN=yy+1→b,
→SP=zz+1→c
(x>0,y>0,z>0)
Do T=AN∩BM nên
{T∈ANT∈BM
⇒{→ST=α→SM+(1−α)→SB→ST=β→SN+(1−β)→SA
⇒α→SM+(1−α)→SB
=β→SN+(1−β)→SA
⇔αxx+1→a+(1−α)→b
=βyy+1→b+(1−β)→a
Vì →a,→b không cùng phương nên ta có
{αxx+1=1−ββyy+1=1−α
⇔{α=xx+y+1β=yx+y+1
⇒→ST=xx+y+1→a+yx+y+1→b
Hoàn toàn tương tự ta có :
→SE=yy+z+1→b+zy+z+1→c,
→SF=zz+x+1→c+xz+x+1→a
Làm tương tự như trên đối với hai giao điểm I=BF∩CT và NF∩PT=J ta được :
→SI=1x+y+z+1(x→a+y→b+z→c),
→SJ=1x+y+z+2(x→a+y→b+z→c)
Suy ra →SJ=x+y+z+1x+y+z+2→SI
⇒→SJ=(x+y+z+1)→IJ
Vậy S,I,J thẳng hàng và
SIIJ=x+y+z+1
=SMMA+SNNB+SPPC+1
Câu 3: Cho hình hộp ABCD.A'B'C'D'. Xác định vị trí các điểm M,N lần lượt trên AC và DC' sao cho MN∥BD'. Tính tỉ số MNBD' bằng?
A. 13
B. 12
C. 1
D. 23
Đáp án: A
Giải thích:
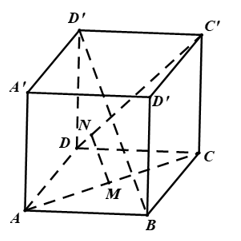
→BA=→a,→BC=→b,→BB'=→c
Giả sử →AM=x→AC,→DN=y→DC'
Dễ dàng có các biểu diễn →BM=(1−x)→a+x→b
và →BN=(1−y)→a+→b+y→c.
Từ đó suy ra
→MN=(x−y)→a+(1−x)→b+y→c(1)
Để MN∥BD' thì
→MN=z→BD'=z(→a+→b+→c)(2)
Từ (1) và (2) ta có:
(x−y)→a+(1−x)→b+y→c
=z(→a+→b+→c)
⇔(x−y−z)→a+(1−x−z)→b
+(y−z)→c=→0
⇔{x−y−z=01−x−z=0y−z=0
⇔{x=23y=13z=13
Vậy các điểm M,N được xác định bởi →AM=23→AC,→DN=13→DC'
Ta cũng có
→MN=z→BD'=13→BD'
⇒MNBD'=13
Câu 4. Cho tứ diện ABCD. Lấy các điểm M, N, P, Q lần lượt thuộc AB, BC, CD, DA sao cho
→AM=13→AB,→BN=23→BC,
→AQ=12→AD,→DP=k→DC.
Hãy xác định k để M, N, P, Q đồng phẳng.
A. k=12
B. k=13
C. k=14
D. k=15
Đáp án: A
Giải thích:
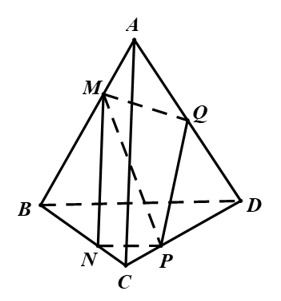
Cách 1.
Ta có →AM=13→AB
⇒→BM−→BA=−13→BA
⇒→BM=23→BA
Lại có →BN=23→BC do đó MN∥AC
Vậy Nếu M,N,P,Q đồng phẳng thì
(MNPQ)∩(ACD)=PQ∥AC
⇒PCPD=QAQD=1 hay →DP=12→DC
⇒k=12.
Cách 2. Đặt →DA=→a,→DB=→b,→DC=→c thì không khó khăn ta có các biểu diễn
→MN=−23→a+23→b, →MP=−23→a−13→b+k→c,
→MN=−16→a−13→b
Các điểm M,N,P,Q đồng phẳng khi và chỉ khi các vec tơ →MN,→MP,→MQ đồng phẳng
⇔∃x,y:→MP=x→MN+y→MQ
⇔−23→a−13→b+k→c
=x(−23→a+23→c)
+y(−16→a−13→b)
Do các vec tơ →a,→b,→c không đồng phẳng nên điều này tương đương với
{−23x−16y=−23−13y=−1323x=k
⇔x=34,y=1,k=12.
Câu 5: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Vì I là trung điểm đoạn AB nên từ O bất kì ta có: →OI=12(→OA+→OB).
B. Vì →AB+→BC+→CD+→DA=→0 nên bốn điểm A, B, C, D đồng phẳng.
C. Vì →NM+→NP=→0 nên N là trung điểm đoạn NP.
D. Từ hệ thức →AB=2→AC−8→AD ta suy ra ba vectơ →AB, →AC, →AD đồng phẳng.
Đáp án: B
Giải thích:
Do →AB+→BC+→CD+→DA=→0 đúng với mọi điểm A,B,C,D nên câu B sai.
Câu 6: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Ba véctơ ⇀a,⇀b,⇀c đồng phẳng khi và chỉ khi ba véctơ đó có giá thuộc một mặt phẳng
B. Ba tia Ox,Oy,Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.
C. Cho hai véctơ không cùng phương ⇀a và ⇀b. Khi đó ba véctơ ⇀a,⇀b,⇀c đồng phẳng khi và chỉ khi có cặp số m,n sao cho ⇀c=m⇀a+n⇀b, ngoài ra cặp số m,n là duy nhất.
D. Nếu có m⇀a+n⇀b+p⇀c=⇀0 và một trong ba số m,n,p khác 0 thì ba véctơ ⇀a,⇀b,⇀c đồng phẳng.
Đáp án: A
Giải thích:
Ba véctơ ⇀a,⇀b,⇀c đồng phẳng khi và chỉ khi ba véctơ đó có giá song song hoặc thuộc một mặt phẳng. Câu A sai
Câu 7: Gọi M,N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MN và P là 1 điểm bất kỳ trong không gian. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: →IA+(2k−1)→IB+k→IC+→ID=→0
A. k=2
B. k=4
C. k=1
D. k=0
Đáp án: C
Giải thích:
Ta chứng minh được →IA+→IB+→IC+→ID=→0 nên k=1
Câu 8: Cho ba vectơ →a, →b, →c. Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu →a, →b, →c không đồng phẳng thì từ m→a+n→b+p→c=→0 ta suy ra m=n=p=0
B. Nếu có m→a+n→b+p→c=→0, trong đó m2+n2+p2>0 thì →a, →b, →c đồng phẳng.
C. Với ba số thực m, n, p thỏa mãn m+n+p≠0 ta có m→a+n→b+p→c=→0 thì →a, →b, →c đồng phẳng.
D. Nếu giá của →a, →b, →c đồng qui thì →a, →b, →c đồng phẳng.
Đáp án: D
Giải thích:
Câu D sai. Ví dụ phản chứng 3 cạnh của hình chóp tam giác đồng qui tại 1 đỉnh nhưng chúng không đồng phẳng.
Câu 9: Cho hình lăng trụ ABCA'B'C', M là trung điểm của. Đặt →CA=→a, →CB=→b,→AA'=→c. Khẳng định nào sau đây đúng?
A. →AM=→a+→c−12→b
B. →AM=→b+→c−12→a
C. →AM=→b−→a+12→c
D. →AM=→a−→c+12→b
Đáp án: C
Giải thích:
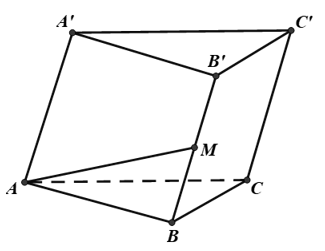
Ta có →AM=→AB+→BM
=→CB−→CA+12→BB'
=→b−→a+12→c
Câu 10: Cho hình lăng trụ tam giác ABCA'B'C'. Đặt →AA'=→a,→AB=→b,→AC=→c, →BC=→d. Trong các biểu thức véctơ sau đây, biểu thức nào đúng.
A. →a=→b+→c
B. →a+→b+→c+→d=→0
C. →b−→c+→d=0
D. →a+→b+→c=→d
Đáp án: C
Giải thích:
Ta có: →b−→c+→d
=→AB−→AC+→BC
=→CB+→BC=→0
Câu 11: Cho tứ diện ABCD và I là trọng tâm tam giác ABC. Đẳng thức đúng là.
A. 6→SI=→SA+→SB+→SC
B. →SI=→SA+→SB+→SC
C. →SI=3(→SA−→SB+→SC)
D. →SI=13→SA+13→SB+13→SC
Đáp án: D
Giải thích:
Vì I là trọng tâm tam giác ABC nên
→SA+→SB+→SC=3→SI
⇔→SI=13→SA+13→SB+13→SC
Câu 12: Trong các mệnh đề sau, mệnh đề nào đúng.
A. Ba véctơ đồng phẳng là ba véctơ cùng nằm trong một mặt phẳng.
B. Ba véctơ →a,→b,→c đồng phẳng thì có →c=m→a+n→b với m,n là các số duy nhất.
C. Ba véctơ không đồng phẳng khi có →d=m→a+n→b+p→c với →d là véctơ bất kì.
D. Ba véctơ đồng phẳng là ba véctơ có giá cùng song song với một mặt phẳng.
Đáp án: D
Giải thích:
Câu A sai vì ba véctơ đồng phẳng là ba véctơ có giá cùng song song với cùng một mặt phẳng.
Câu B sai vì thiếu điều kiện 2 véctơ →a,→b không cùng phương.
Câu C sai vì →d=m→a+n→b+p→c với →d là véctơ bất kì không phải là điều kiện để 3 véctơ →a, →b, →c đồng phẳng.
Câu 13: Cho hình hộp ABCD.A'B'C'D'. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: →AC+→BA'+k(→DB+→C'D)=→0.
A. k=0
B. k=1
C. k=4
D. k=2
Đáp án: B
Giải thích:
Với k=1 ta có:
→AC+→BA'+1.(→DB+→C'D)
=→AC+→BA'+→C'B
=→AC+→C'A'
=→AC+→CA=→0
Câu 14: Cho hình chóp S.ABC. Lấy các điểm A',B',C' lần lượt thuộc các tia SA,SB,SC sao cho SA=a.SA', SB=b.SB', SC=c.SC', trong đó a,b,c là các số thay đổi. Tìm mối liên hệ giữa a,b,c để mặt phẳng (A'B'C') đi qua trọng tâm của tam giác ABC.
A. a+b+c=3
B. a+b+c=4
C. a+b+c=2
D. a+b+c=1
Đáp án: A
Giải thích:
Nếu a=b=c=1 thì SA=SA',SB=SB',SC=SC' nên (ABC)≡(A'B'C').
Suy ra (A'B'C') đi qua trọng tâm của tam giấc ABC
=> a+b+c=3 là đáp án đúng.
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt →SA=→a,→SB=→b,→SC=→c, →SD=→d. Khẳng định nào sau đây đúng.
A. →a+→c=→d+→b
B. →a+→c+→d+→b=→0
C. →a+→d=→b+→c
D. →a+→b=→c+→d
Đáp án: A
Giải thích:
Gọi O là tâm hình bình hành ABCD. Ta có:
{→a+→c=→SA+→SC=2→SO→b+→d=→SB+→SD=2→SO
=> →a+→c=→d+→b
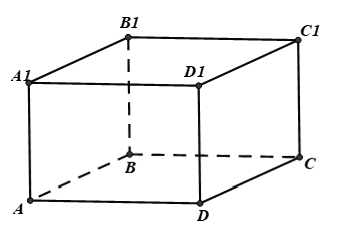
Câu 16: Cho hình hộp ABCD.A1B1C1D1. Trong các khẳng định sau, khẳng định nào sai?
A. →AC1+→A1C=2→AC
B. →AC1+→CA1+2→C1C=→0
C. →AC1+→A1C=→AA1
D. →CA1+→AC=→CC1
Đáp án: A
Giải thích:
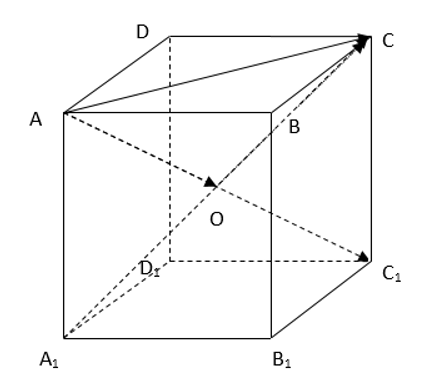
+ Gọi O là tâm của hình hộp ABCD.A1B1C1D1.
+ Vận dụng công thức trung điểm để kiểm tra.
Câu 17: Hãy chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Tứ giác ABCD là hình bình hành nếu →AB+→BC+→CD+→DA=→O.
B. Tứ giác ABCD là hình bình hành nếu →AB=→CD.
C. Cho hình chóp S.ABCD. Nếu có →SB+→SD=→SA+→SC thì tứ giác ABCD là hình bình hành.
D. Tứ giác ABCD là hình bình hành nếu →AB+→AC=→AD.
Đáp án: C
Giải thích:

→SB+→SD=→SA+→SC
⇔→SA+→AB+→SA+→AD
=→SA+→SA+→AC.
⇔→AB+→AD=→AC.
⇔ABCD là hình bình hành
Câu 18: Cho hình lập phương ABCD.EFGH có cạnh bằng a. Ta có →AB.→EG bằng?
A. a2√2
B. a2
C. a2√3
D. a2√22
Đáp án: B
Giải thích:
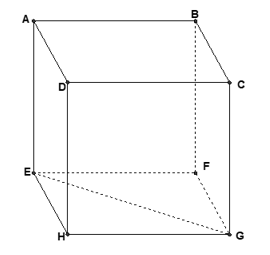
→AB.→EG=→AB.(→EF+→EH)
=→AB.→EF+→AB→.EH
=→AB2+→AB.→AD (→EH=→AD)
=a2(Vì →AB⊥→AD).
Câu 19: Trong không gian cho điểm O và bốn điểm A,B,C,D không thẳng hàng. Điều kiện cần và đủ để A,B,C,D tạo thành hình bình hành là:
A. →OA+12→OB=→OC+12→OD
B. →OA+12→OC=→OB+12→OD
C. →OA+→OC=→OB+→OD
D. →OA+→OB+→OC+→OD=→0
Đáp án: C
Giải thích:

→OA+→OC=→OB+→OD
⇔→OA+→OA+→AC
=→OA+→AB+→OA+→BC
⇔→AC=→AB+→BC
Câu 20: Cho hình hộp ABCD.A'B'C'D'. Gọi I và K lần lượt là tâm của hình bình hành ABB’ và . Khẳng định nào sau đây sai ?
A. Bốn điểm I, K, C, A đồng phẳng
B.
C. Ba vectơ không đồng phẳng.
D.
Đáp án: C
Giải thích:
A. Đúng vì cùng thuộc
B. Đúng vì
C. Sai vì
ba véctơ đồng phẳng.
D. Đúng vì theo câu C
Câu 21: Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M,N sao cho , . Gọi P,Q lần lượt là trung điểm của AD và BC. Trong các khẳng định sau, khẳng định nào sai?
A. Các vectơ đồng phẳng.
B. Các vectơ đồng phẳng.
C. Các vectơ đồng phẳng.
D. Các vectơ đồng phẳng.
Đáp án: A
Giải thích:
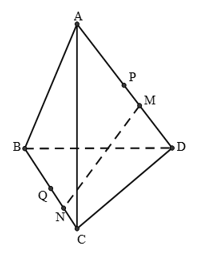
A. Sai vì
không đồng phẳng.
B. Đúng vì
: đồng phẳng.
C. Đúng. Bằng cách biểu diễn tương tự như trên ta có
D. Đúng. Biểu diễn giống đáp án A ta có .
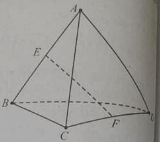
Câu 25: Cho tứ diện ABCD có các cạnh đều bằng a. Hãy chỉ ra mệnh đề sai trong các mệnh đề sau đây:
A.
B.
C.
D. hay
Đáp án: C
Giải thích:
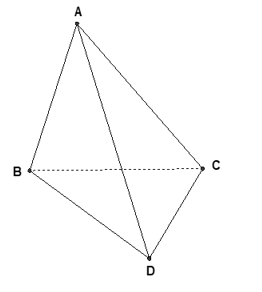
Vì ABCD là tứ diện đều nên các tam giác ABC, BCD, CDA, ABD là các tam giác đều.
A. Đúng vì
B. Đúng vì
C. Sai vì
D. Đúng vì
Câu 26: Cho tứ diện ABCD. Đặt gọi G là trọng tâm của tam giác BCD. Trong các đẳng thức sau, đẳng thức nào đúng?
A.
B.
C.
D.
Đáp án: B
Giải thích:
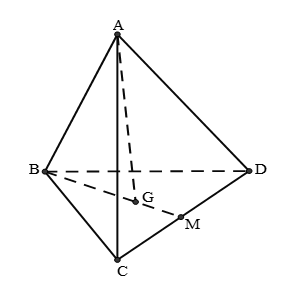
Gọi M là trung điểm BC.
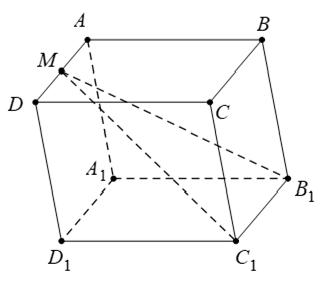
Câu 27: Cho hình hộp . Gọi M là trung điểm AD. Chọn đẳng thức đúng.
A.
B.
C.
D.
Đáp án: B
Giải thích:
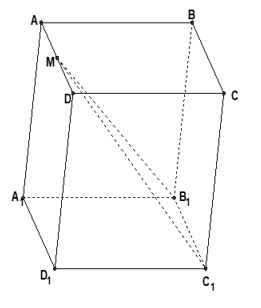
A. Sai vì
B. Đúng vì
C. Sai. theo câu B suy ra
D. Đúng vì
Câu 28: Cho tứ diện ABCD và điểm G thỏa mãn (G là trọng tâm của tứ diện). Gọi là giao điểm của GA và mp. Trong các khẳng định sau, khẳng định nào đúng?
A.
B.
C.
D.
Đáp án: C
Giải thích:
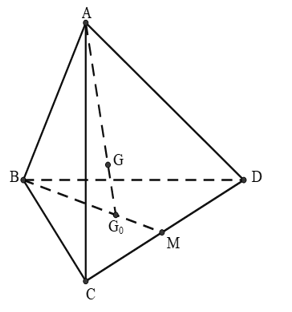
Theo đề: là giao điểm của GA và mp
là trọng tâm tam giác BCD.
Ta có:
Câu 29: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD, BC. Trong các khẳng định sau, khẳng định nào sai?
A. Các vectơ đồng phẳng.
B. Các vectơ không đồng phẳng.
C. Các vectơ đồng phẳng.
D. Các vectơ đồng phẳng.
Đáp án: C
Giải thích:
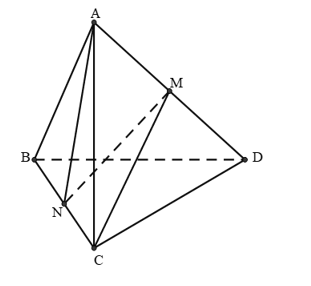
A. Đúng vì
B. Đúng vì từ N ta dựng véctơ bằng véctơ thì không nằm trong mặt phẳng .
C. Sai. Tương tự đáp án B thì không nằm trong mặt phẳng .
D. Đúng vì
Câu 30: Cho tứ diện ABCD. Người ta định nghĩa “ G là trọng tâm tứ diện ABCD khi ”. Khẳng định nào sau đây sai ?
A. G là trung điểm của đoạn IJ (I , J lần lượt là trung điểm AB và CD)
B. G là trung điểm của đoạn thẳng nối trung điểm của AC và BD
C. G là trung điểm của đoạn thẳng nối trung điểm của AD và BC
D. Chưa thể xác định được.
Đáp án: D
Giải thích:
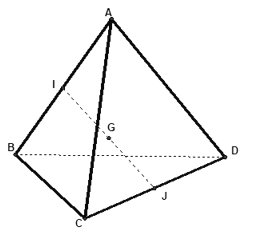
Ta có:
G là trung điểm IJ nên đáp án A đúng
Tương tự cho đáp án B và C cũng đúng.
Câu 31: Cho tứ diện ABCD, E và F lần lượt là trung điểm của AB và CD, AB = 2a, CD = 2b và EF = 2c. M là một điểm bất kì.
MA2 + MB2 bằng:
A. 2ME2 + 2a2
B. 2MF2 + 2a2
C. 2ME2 + 2b2
D. 2MF2 + 2b2
Đáp án: B
Giải thích:
MA2 = (ME→ + EA→ )2 = ME2 + EA2 + 2ME→.EA→
MB2 = (ME→ + EB→ )2 = ME2 + EB2 + 2ME→.EB→
Suy ra: MA2 + MB2 = 2ME2 + 2a2 (do EA→ + EB→ = 0→)
Câu 32: Cho hình hộp ABCD.A1B1C1D1 với tâm O. Chọn đẳng thức sai.
Đáp án: A
Giải thích:
Áp dụng quy tắc hình bình hành ta có :
Câu 33: Cho hình hộp ABCD.A1B1C1D1. Chọn đẳng thức sai?
Đáp án: C
Giải thích:
Chọn D.
Ta xét các phương án :
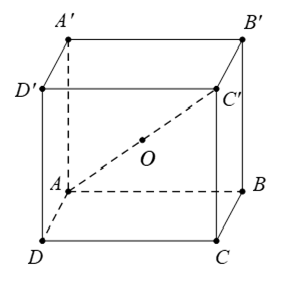
Câu 34: Cho hình lập phương ABCD.A1B1C1D1. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng?
Đáp án: B
Giải thích:
Theo quy tắc hình hộp:
Câu 35: Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?
Đáp án: D
Giải thích:
+ A đúng theo định nghĩa trọng tâm tứ diện.
+ B đúng do tính chất của trọng tâm tứ diện.
+ Do G là trọng tâm tứ diện ABCD
⇒ D đúng
Câu 36: Cho tứ diện ABCD và I là trọng tâm tam giác ABC. Đẳng thức đúng là.
Đáp án: D
Giải thích:
Vì I là trọng tâm tam giác ABC nên:
Câu 37: Cho hình hộp ABCD.A’B’C’D’. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai ?
Đáp án: C
Giải thích:
Câu 38: Cho hình hộp ABCD. A’B’C’D’ tâm O. Khẳng định nào dưới đây là sai ?
Đáp án: C
Giải thích:
Dựa vào đáp án, ta thấy rằng:
Câu 39: Cho hình hộp ABCD.A1B1C1D1. Gọi M là trung điểm của AD. Khẳng định nào dưới đây là đúng ?
Đáp án: B
Giải thích:
Dựa vào đáp án, ta thấy rằng:
Câu 40: Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức P = MA2 + MB2 + MC2 đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC.
B. M là tâm đường tròn ngoại tiếp tam giác ABC.
C. M là trực tâm tam giác BAC
D. M là tâm đường tròn nội tiếp tam giác ABC.
Đáp án: A
Giải thích:
Gọi G là trọng tâm tam giác ABC ⇒ G cố định và GA→ + GB→ + GC→ = 0→
Dấu bằng xảy ra
Vậy Pmin = GA2 + GB2 + GC2 với M ≡ G là trọng tâm tam giác ABC
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác
Trắc nghiệm Hai đường thẳng vuông góc có đáp án
Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
Trắc nghiệm Hai mặt phẳng vuông góc có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án