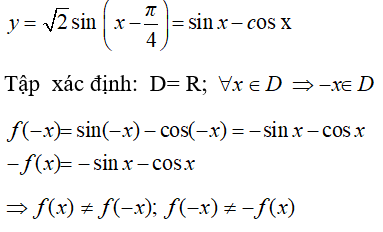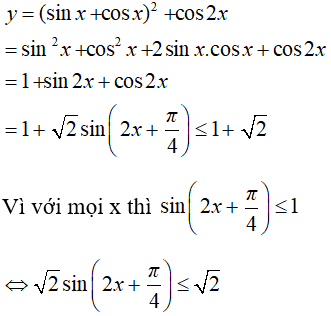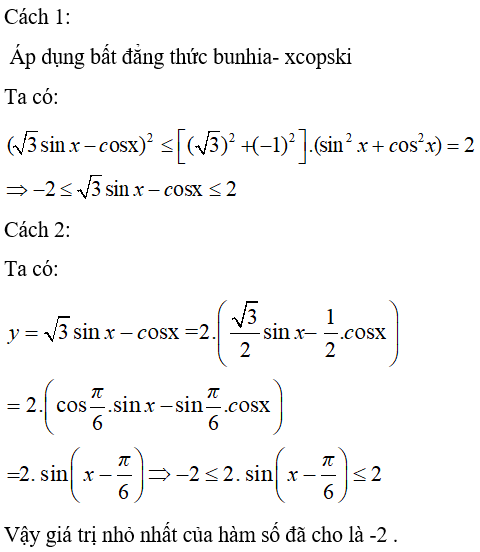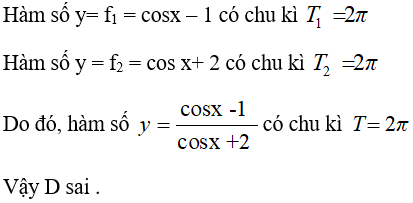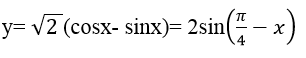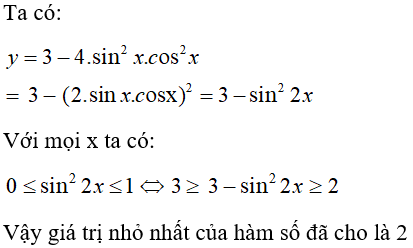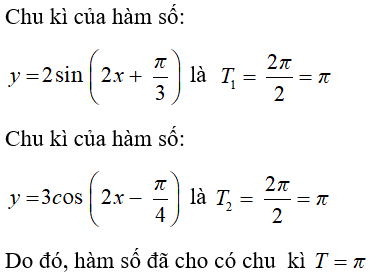TOP 40 câu Trắc nghiệm Hàm số lượng giác (có đáp án 2023) – Toán 11

Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 1: Hàm số lượng giác có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 1.

1 4,810 12/01/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác

Bài giảng Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác

Câu 1: Tìm tập xác định của hàm số $y = \sqrt{1 + s inx}$

A. $D = [- 1;+ \infty)$

B. $D = ℝ$

C. $D = ℝ \ \{\frac{π}{2} + k π; k \in ℤ\}$

D. $D = (- \infty; - 1]$

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số $y = \sqrt{1 + \sin x}$ xác định

$\Leftrightarrow 1 + \sin x \geq 0$

$\Leftrightarrow \sin x \geq - 1$ luôn đúng $\forall x \in ℝ$

Câu 2: Cho $P = \sin (π + α) . \cos (π - α)$ và $Q = \sin (\frac{π}{2} - α) . \cos (\frac{π}{2} + α)$

Mệnh đề nào dưới đây là đúng

A. $P + Q = 2$

B. $P + Q = 0$

C. $P + Q = - 1$

D. $P + Q = 1$

Hiển thị đáp án

Đáp án: B

Giải thích:

$P = \sin (π + α) \cos (π - α)$

$= \sin α \cos α;$

$Q = \sin (\frac{π}{2} - α) \cos (\frac{π}{2} + α)$

$= - \cos α \sin α$

Vậy $P + Q = 0$ .

Câu 3: Tập xác định của hàm số $y = \frac{1}{2 \cos x - \sqrt{3}}$ là

A. $D = ℝ \ \{\frac{π}{6} + k 2 π, k \in ℤ\}$

B. $D = ℝ \ \{\frac{π}{3} + k 2 π, k \in ℤ\}$

C. $D = ℝ \ \{\frac{π}{6} + k 2 π, - \frac{π}{6} + k 2 π, k \in ℤ\}$

D. $D = ℝ \ \{\frac{π}{3} + k 2 π, \frac{2 π}{3} + k 2 π, k \in ℤ\}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có y xác định khi $2 \cos x - \sqrt{3} \neq 0$

$\Leftrightarrow \cos x \neq \frac{\sqrt{3}}{2}$

$\Leftrightarrow \{\begin{cases} x \neq \frac{π}{6} + k 2 π \\ x \neq - \frac{π}{6} + k 2 π \end{cases}$ .

Câu 4: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 3 \sin 2 x - 5$ lần lượt là

A. -8 và -2

B. 2 và 8

C. -5 và 2

D. - và 3

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $- 1 \leq \sin 2 x \leq 1$

$\begin{array}{l} \Leftrightarrow - 3 \leq 3 \sin 2 x \leq 3 \\ \Leftrightarrow - 8 \leq 3 \sin 2 x - 5 \leq - 2 \end{array}$

Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 3 \sin 2 x - 5$ lần lươt là -8 và -2 .

Câu 5: Cho $α \in (- \frac{π}{3}; \frac{π}{3})$ . Trong những khẳng định sau, khẳng định nào đúng?

A. $\cos (α + \frac{π}{3}) > 0$

B. $\cot (α + \frac{π}{3}) > 0$

C. $\tan (α + \frac{π}{3}) > 0$

D. $\sin (α + \frac{π}{3}) > 0$

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì $- \frac{π}{3} < α < \frac{π}{3}$

$\to 0 < α + \frac{π}{3} < \frac{2 π}{3}$

suy ra $\sin (α + \frac{π}{3}) > 0$ .

Câu 6: Cho $α \in (\frac{π}{2}; π); \sin α = \frac{1}{3}$ . Giá trị của biểu thức $P = \sin α + \cos α + 1$ là

A. $\frac{4 + 2 \sqrt{2}}{3}$

B. $\frac{12 + 2 \sqrt{2}}{9}$

C. $\frac{12 - 2 \sqrt{2}}{9}$

D. $\frac{4 - 2 \sqrt{2}}{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\cos^{2} α = 1 - \sin^{2} α = 1 - \frac{1}{9} = \frac{8}{9},$

vì $α \in (\frac{π}{2}; π)$ nên $\cos α = - \frac{2 \sqrt{2}}{3}$

Vậy $P = \sin α + \cos α + 1$

$= \frac{1}{3} - \frac{2 \sqrt{2}}{3} + 1$

$= \frac{4 - 2 \sqrt{2}}{3}$

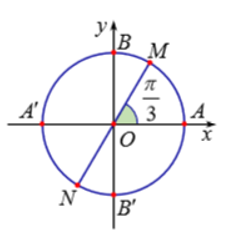
Câu 7: Trên hình vẽ sau các điểm M , N là những điểm biểu diễn của các cung có số đo là:

Trắc nghiệm Hàm số lượng giác có đáp án – Toán lớp 11 (ảnh 3)

A. $\frac{π}{3} + k 2 π, k \in ℤ$

B. $\frac{π}{3} + k \frac{π}{2}; k \in ℤ$

C. $\frac{4 π}{3} + k π, k \in ℤ$

D. $\frac{- π}{3} + k π, k \in ℤ$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: Cung có số đo $\frac{4 π}{3} + k π, k \in ℤ$ biểu diễn hai điểm M, N có số đo cung lần lượt là $\frac{π}{3}; \frac{4 π}{3}$ .

Câu 8: Cho $\cot α = 2$ Giá trị của biểu thức $P = \frac{\sin α + \cos α}{\sin α - c o s α}$ là

A. -3

B. 3

C. 1

D. -1

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì $\cot α = 2$ nên $\sin α \neq 0$

Chia tử và mẫu của biểu thức P cho $\sin α$

ta được $P = \frac{1 + \cot α}{1 - \cot α} = \frac{1 + 2}{1 - 2} = - 3$ .

Câu 9: Đồ thị hàm số trên hình vẽ là đồ thị của hàm số nào

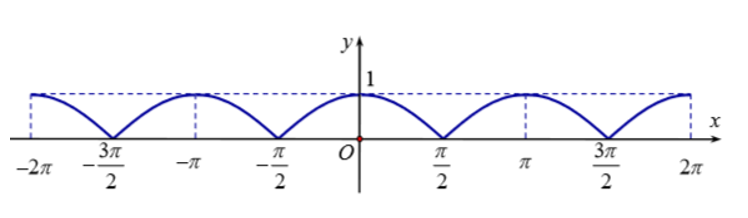
Trắc nghiệm Hàm số lượng giác có đáp án – Toán lớp 11 (ảnh 4)

A. $y = |\tan x|$

B. $y = |\cos 2 x|$

C. $y = |\cos x|$

D. $y = |\sin x|$

Hiển thị đáp án

Đáp án: C

Giải thích:

Nhận xét:

+) $x = \frac{π}{2} + k π (k \in ℤ)$ thì $y = 0$ . Suy ra loại B và D

+) $x = 0$ thì y = . Suy ra loại A

Vậy đáp án đúng là C.

Câu 10: Đẳng thức nào sau đây là đúng?

A. $\sin^{4} x + \cos^{4} x = 1 - \frac{1}{2} \sin^{2} 2 x$

B. $\sin 4 x = 2 \sin x \cos x \cos 2 x$

C. $\cos 2 x = (\sin x - \cos x) (\sin x + \cos x)$

D. $\cos (a + b) = \sin a \sin b - \cos a \cos b$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\sin^{4} x + \cos^{4} x$

$= {(\sin^{2} x + \cos^{2} x)}^{2} - 2 \sin^{2} x \cos^{2} x$

$= 1 - \frac{1}{2} \sin^{2} 2 x$ .

Câu 11: Tập xác định của hàm số $y = \frac{\sin 2 x + \cos x}{\tan x - \sin x}$ là

A. $ℝ \ \{k π, k \in ℤ\}$

B. $ℝ \ \{\frac{π}{2} + k π; k \in ℤ\}$

C. $ℝ \ \{k \frac{π}{2}; k \in ℤ\}$

D. $ℝ \ \{\frac{π}{2} + k π, k 2 π, k \in ℤ\}$

Hiển thị đáp án

Đáp án: C

Giải thích:

ĐKXĐ: $\{\begin{cases} \tan x - \sin x \neq 0 \\ \cos x \neq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} \sin x (1 - \cos x) \neq 0 \\ \cos x \neq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} \sin x \neq 0 \\ \cos x \neq 1 \\ \cos x \neq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq k π \\ x \neq k 2 π \\ x \neq \frac{π}{2} + k π \end{cases} (k \in ℤ)$ .

Câu 12: Tập xác định của hàm số $y = \sqrt{1 + \cot^{2} 2 x}$ là

A. $D = ℝ \ \{k 180 °; k \in ℤ\}$

B. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$

C. $D = ℝ \ \{k \frac{π}{2}, k \in ℤ\}$

D. $D = ℝ$

Hiển thị đáp án

Đáp án: C

Giải thích:

ĐKXĐ: $\{\begin{cases} 1 + \cot^{2} 2 x \geq 0 (\forall x \in ℝ) \\ \sin 2 x \neq 0 \end{cases}$

$\Leftrightarrow x \neq k \frac{π}{2} (k \in ℤ)$ .

Câu 13: Hàm số $y = \sqrt{\frac{\sin (x + \frac{π}{6}) + 3}{1 - \cos x}}$ có tập xác định là

A. $D = ℝ \ \{k 2 π, k \in ℤ\}$

B. $D = ℝ \ \{k π; k \in ℤ\}$

C. $D = ℝ \ \{\frac{π}{2} + k 2 π; k \in ℤ\}$

D. $D = ℝ \ \{\frac{π}{2} + k π; k \in ℤ\}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số xác định khi:

$1 - \cos x \neq 0$

$\Leftrightarrow x \neq k 2 π, k \in ℤ$

Câu 14: Hàm số nào tuần hoàn với chu kì $T = 3 π$

A. $y = 2 \cos 2 x$

B. $y = \sin (\frac{x}{3})$

C. $y = \sin (\frac{2 x}{3})$

D. $y = 2 \sin 3 x$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Chu kì tuần hoàn của hàm số $[\begin{array}{l} \sin (a x) \\ \cos (a x) \end{array}$ là $\frac{2 π}{|a|}$

Chu kì tuần hoàn của hàm số $y = \sin (\frac{2 x}{3})$ là $\frac{2 π}{|a|} = \frac{2 π}{|\frac{2}{3}|} = 3 π$ .

Câu 15: Điều kiện xác định của hàm số $y = \tan 2 x$ là

A. $x \neq \frac{π}{4} + k π (k \in ℤ)$

B. $x \neq \frac{π}{4} + k \frac{π}{2} (k \in ℤ)$

C. $x \neq \frac{π}{8} + k \frac{π}{2} (k \in ℤ)$

D. $x \neq \frac{π}{2} + k π (k \in ℤ)$

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số xác định khi:

$\cos 2 x \neq 0$

$\Leftrightarrow 2 x \neq \frac{π}{2} + k π$

$\Leftrightarrow x \neq \frac{π}{4} + k \frac{π}{2}; k \in ℤ$ .

Câu 16: Tìm mệnh đề đúng trong các mệnh đề sau?

A. Hàm số $y = \sin x$ đồng biên trên mỗi khoảng $(\frac{π}{2} + k 2 π; π + k 2 π)$ và nghịch biên trên mỗi khoảng $(π + k 2 π, k 2 π)$ với $k \in ℤ$

B. Hàm số $y = \sin x$ đồng biên trên mỗi khoảng $(\frac{π}{2} + k 2 π; \frac{3 π}{2} + k 2 π)$ và nghịch biên trên mỗi khoảng $(- \frac{π}{2} + k 2 π, k 2 π)$ với $k \in ℤ$

C. Hàm số $y = \sin x$ đồng biên trên mỗi khoảng $(- \frac{3 π}{2} + k 2 π; \frac{5 π}{2} + k 2 π)$ và nghịch biên trên mỗi khoảng $(\frac{π}{2} + k 2 π, \frac{π}{2} + k 2 π)$ với $k \in ℤ$

D. Hàm số $y = \sin x$ đồng biên trên mỗi khoảng $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ và nghịch biên trên mỗi khoảng $(\frac{π}{2} + k 2 π, \frac{3 π}{2} + k 2 π)$ với $k \in ℤ$

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số $y = sinx$ đồng biến trên mỗi khoảng $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ và nghịch biến trên mỗi khoảng $(\frac{π}{2} + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ$ .

Câu 17: Tập xác định của hàm số $y = \frac{\cot x}{1 + \cos x}$ là

A. $D = ℝ \ \{k π, k \in ℤ\}$

B. $D = ℝ \ \{π + k 2 π, k \in ℤ\}$

C. $D = ℝ \ \{- \frac{π}{2} + k π; k \in ℤ\}$

D. $D = ℝ \ \{k \frac{π}{2}; k \in ℤ\}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Điều kiện $\{\begin{cases} \sin x \neq 0 \\ 1 + \cos x \neq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq k π \\ x \neq π + k 2 π \end{cases}$

$\Leftrightarrow x \neq k π, k \in ℤ$

Vậy TXĐ của hàm số là $D = ℝ \ \{k π; k \in ℤ\}$ .

Câu 18: Tập xác định của hàm số $y = \cot (x - \frac{π}{4}) + \tan (x - \frac{π}{4})$ là

A. $D = ℝ \ \{k π, k \in ℤ\}$

B. $D = ℝ \ \{k 2 π, k \in ℤ\}$

C. $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2}; k \in ℤ\}$

D. $D = ℝ \ \{k \frac{π}{2}; k \in ℤ\}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện $\{\begin{cases} \sin (x - \frac{π}{4}) \neq 0 \\ \cos (x - \frac{π}{4}) \neq 0 \end{cases}$

$\Leftrightarrow \sin (2 x - \frac{π}{2}) \neq 0$

$\Leftrightarrow 2 x - \frac{π}{2} \neq k π$

$\Leftrightarrow x \neq \frac{π}{4} + k \frac{π}{2}; k \in ℤ$

Vậy TXĐ của hàm số là $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2}; k \in ℤ\}$ .

Câu 19: Tập xác định của hàm số $y = \sqrt{\frac{1 + \cos x}{1 - \cos x}}$ là

A. $D = ℝ \ \{k π, k \in ℤ\}$

B. $D = ℝ$

C. $D = ℝ \ \{k 2 π; k \in ℤ\}$

D. $D = ℝ \ \{\frac{π}{2} + k 2 π; k \in ℤ\}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện $\{\begin{cases} \frac{1 + \cos x}{1 - \cos x} \geq 0 \\ 1 - \cos x \neq 0 \end{cases}$

$\Leftrightarrow 1 - \cos x \neq 0$

$\Leftrightarrow \cos x \neq 1 \Leftrightarrow x \neq k 2 π, k \in ℤ$

Vậy TXĐ của hàm số là $D = ℝ \ \{k 2 π; k \in ℤ\}$ .

Câu 20: Giá trị lớn nhất của hàm số $y = \cos x - 3 \sin x$ là

A. -2

B. 4

C. 10

D. $\sqrt{10}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi $y_{0}$ là một giá nằm trong tập giá trị của hàm số $y = \cos x - 3 \sin x$ .

Khi đó, tồn tại $x \in ℝ$ thỏa mãn phương trình $y_{0} = \cos x - 3 \sin x (1)$

Điều kiện để (1) có nghiệm là

${(- 3)}^{2} + 1^{2} \geq y_{0}^{2}$

$\Leftrightarrow y_{0}^{2} \leq 10$

$\Leftrightarrow - \sqrt{10} \leq y_{0} \leq \sqrt{10}$

Vậy giá trị lớn nhất của hàm số bằng $\sqrt{10}$ .

Câu 21: Tập giá trị của hàm số $y = 1 - 2 |\sin 2 x|$ là

A. $[1; 3]$

B. $[- 1; 1]$

C. $[- 1; 3]$

D. $[- 1; 0]$

Hiển thị đáp án

Đáp án: B

Giải thích:

Do $- 1 \leq \sin 2 x \leq 1$

$\Rightarrow 0 \leq |\sin 2 x| \leq 1$

$\Leftrightarrow - 2 \leq - 2 |\sin 2 x| \leq 0$

$\Leftrightarrow - 1 \leq 1 - 2 |\sin 2 x| \leq 1$

Ta có: $y = - 1 \Leftrightarrow 1 - 2 |\sin 2 x| = - 1$

$\Leftrightarrow |\sin 2 x| = 1 \Leftrightarrow \cos 2 x = 0$

$\Leftrightarrow 2 x = \frac{π}{2} + k π$

$\Leftrightarrow x = \frac{π}{4} + k \frac{π}{2} (k \in ℤ)$

$y = 1 \Leftrightarrow 1 - 2 |\sin 2 x| = 1$

$\Leftrightarrow |\sin 2 x| = 0 \Leftrightarrow \sin 2 x = 0$

$\Leftrightarrow 2 x = k π$

$\Leftrightarrow x = k \frac{π}{2} (k \in ℤ)$

Vậy tập giá trị của hàm số là $[- 1; 1]$ .

Câu 22: Tập giá trị của hàm số $y = 2 + \sqrt{1 - \sin^{2} 2 x}$ là

A. $[1; 2]$

B. $[0; 2]$

C. $[1; 3]$

D. $[2; 3]$

Hiển thị đáp án

Đáp án: D

Giải thích:

Do $- 1 \leq \sin 2 x \leq 1$

$\Rightarrow 0 \leq \sin^{2} 2 x \leq 1$

$\Leftrightarrow 0 \leq 1 - \sin^{2} 2 x \leq 1$

$\Leftrightarrow 0 \leq \sqrt{1 - \sin^{2} 2 x} \leq 1$

$\Leftrightarrow 2 \leq 2 + \sqrt{1 - \sin^{2} 2 x} \leq 3$

Ta có $y = 2$

$\Leftrightarrow 2 + \sqrt{1 - \sin^{2} 2 x} = 2$

$\Leftrightarrow \sqrt{1 - \sin^{2} 2 x} = 0$

$\Leftrightarrow \cos 2 x = 0$

$\Leftrightarrow x = \frac{π}{4} + k \frac{π}{2} (k \in ℤ)$

$y = 3$

$\Leftrightarrow 2 + \sqrt{1 - \sin^{2} 2 x} = 3$

$\Leftrightarrow \sqrt{1 - \sin^{2} 2 x} = 1$

$\Leftrightarrow \sin 2 x = 0$

$\Leftrightarrow x = k \frac{π}{2} (k \in ℤ)$

Vậy tập giá trị của hàm số $y = 2 + \sqrt{1 - \sin^{2} 2 x}$ là $[2; 3]$ .

Câu 23: Giá trị nhỏ nhất của hàm số $y = 2 + \sin x \cos x$ là

A. $\frac{5}{2}$

B. $\frac{3}{2}$

C. $\frac{2}{3}$

D. 1

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $y = 2 + \sin x \cos x = 2 + \frac{1}{2} \sin 2 x$

Ta lại có

$- 1 \leq \sin 2 x \leq 1, \forall x$

$\Leftrightarrow - \frac{1}{2} \leq \frac{1}{2} \sin 2 x \leq \frac{1}{2}, \forall x$

$\Leftrightarrow \frac{3}{2} \leq 2 + \frac{1}{2} \sin 2 x \leq \frac{5}{2}, \forall x$

$\Leftrightarrow \frac{3}{2} \leq y \leq \frac{5}{2}, \forall x$

$y = \frac{3}{2} \Leftrightarrow \sin 2 x = - 1$

$\Leftrightarrow 2 x = - \frac{π}{2} + k 2 π$

$\Leftrightarrow x = - \frac{π}{4} + k π; k \in ℤ$

Vậy giá trị nhỏ nhất của hàm số $y = 2 + \sin x \cos x$ là $\frac{3}{2}$ .

Câu 24: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 7 - 2 \cos (x + \frac{π}{4})$ lần lượt là

A. -2 và 7

B. -2 và 2

C. 5 và 9

D. 4 và 7

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $- 1 \leq \cos (x + \frac{π}{4}) \leq 1, \forall x$

$\Leftrightarrow 2 \geq - 2 \cos (x + \frac{π}{4}) \geq - 2, \forall x$

$\Leftrightarrow 9 \geq 7 - 2 \cos (x + \frac{π}{4}) \geq 5, \forall x$

$\Leftrightarrow 9 \geq y \geq 5, \forall x$

$y = 9 \Leftrightarrow \cos (x + \frac{π}{4}) = - 1$

$\Leftrightarrow x + \frac{π}{4} = π + k 2 π$

$\Leftrightarrow x = \frac{3 π}{4} + k 2 π, k \in ℤ$

$y = 5 \Leftrightarrow \cos (x + \frac{π}{4}) = 1$

$\Leftrightarrow x + \frac{π}{4} = k 2 π$

$\Leftrightarrow x = - \frac{π}{4} + k 2 π, k \in ℤ$

Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 7 - 2 \cos (x + \frac{π}{4})$ lần lượt là 5 và 9.

Câu 25: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 4 \sqrt{s inx + 3} - 1$ lần lượt là

A. $\sqrt{2}$ và 2

B. 2 và 4

C. $4 \sqrt{2}$ và 8

D. $4 \sqrt{2} - 1$ và 7

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$- 1 \leq sinx \leq 1, \forall x$

$\Leftrightarrow 2 \leq s i n x + 3 \leq 4, \forall x$

$\Leftrightarrow \sqrt{2} \leq \sqrt{\sin x + 3} \leq 2, \forall x$

$\Leftrightarrow 4 \sqrt{2} - 1 \leq 4 \sqrt{\sin x + 3} - 1 \leq 7$

$\Leftrightarrow 4 \sqrt{2} - 1 \leq y \leq 7, \forall x$

$y = 4 \sqrt{2} - 1 \Leftrightarrow \sin x = - 1$

$\Leftrightarrow x = - \frac{π}{2} + k 2 π, k \in ℤ$

$y = 7 \Leftrightarrow \sin x = 1$

$\Leftrightarrow x = \frac{π}{2} + k 2 π, k \in ℤ$

Vậy giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 4 \sqrt{\sin x + 3} - 1$ lần lượt là $4 \sqrt{2} - 1$ và 7

Câu 26: Hàm số nào sau đây đồng biên trên khoảng $(\frac{π}{2}; π)$

A. $y = sinx$

B. $y = cosx$

C. $y = \tan x$

D. $y = \cot x$

Hiển thị đáp án

Đáp án: C

Giải thích:

Nhìn vào đồ thị hàm $y = \tan x$ ta thấy trong khoảng $(\frac{π}{2}; π)$ đồ thị hàm số là 1 đường cong đi lên. Do vậy, hàm số đồng biến trên khoảng 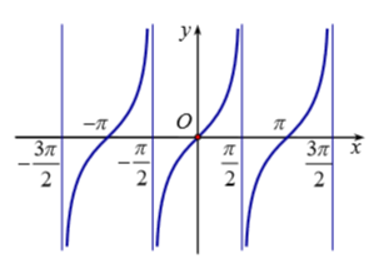$(\frac{π}{2}; π)$ Trắc nghiệm Hàm số lượng giác có đáp án – Toán lớp 11 (ảnh 5)

Câu 27: Để có đồ thị hàm số $y = \cos x$ , ta thực hiện phép tịnh tiến đồ thị $y = \sin x$ theo véctơ:

A. $\vec{v} = (- π; 0)$

B. $\vec{v} = (π; 0)$

C. $\vec{v} = (- \frac{π}{2}; 0)$

D. $\vec{v} = (\frac{π}{2}; 0)$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: Theo biểu thức tọa độ của phép tịnh tiến $\{\begin{cases} x' = x + a \\ y' = y + b \end{cases}$

Khi $\vec{v} = (- \frac{π}{2}; 0)$ ta có

$\{\begin{cases} x' = x - \frac{π}{2} \\ y' = y \end{cases} \Leftrightarrow \{\begin{cases} x = x' + \frac{π}{2} \\ y = y' \end{cases}$

Thay vào $y = \sin x$ ta được

$y' = \sin (\frac{π}{2} + x')$

$= \cos (- x') = \cos x'$ .

Câu 28: Đẳng thức nào sai?

A. $\sin a + \sin b = 2 \sin \frac{a + b}{2} . \cos \frac{a - b}{2}$

B. $\cos a - \cos b = - 2 \sin \frac{a + b}{2} . s i n \frac{a - b}{2}$

C. $1 - \sin x = 2 \sin^{2} (\frac{π}{4} - \frac{x}{2})$

D. $\cos a . \sin b$

$= \frac{1}{2} [\sin (a - b) + \sin (a + b)]$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\cos a . \sin b$

$= \frac{1}{2} [\sin (a - b) + \sin (a + b)]$ .

Câu 29: Chọn khẳng định đúng trong các khẳng định sau:

A. Hàm số $y = \sin 2 x$ là hàm số chẵn

B. Hàm số $y = \sin 2 x$ tuần hoàn với chu kì $T = π$

C. Hàm số $y = \sin 2 x$ tuần hoàn với chu kì $T = 2 π$

D. Đồ thị hàm số $y = \sin 2 x$ nhận trục Oy là trục đối xứng.

Hiển thị đáp án

Đáp án: B

Giải thích:

Chu kì tuần hoàn của hàm số $y = \sin (2 x)$ là $\frac{2 π}{|2|} = \frac{2 π}{|2|} = π$ .

Câu 30: Hàm số nào sau đây là hàm số chẵn?

A. $y = \cos (x - \frac{π}{2})$

B. $y = \tan (x - \frac{π}{2})$

C. $y = \sin (x^{2} - \frac{π}{2})$

D. $y = \cot x$

Hiển thị đáp án

Đáp án: C

Giải thích:

+ Đáp án A sai vì

$f (x) = \cos (x - \frac{π}{2}) = - \sin x$

$\Rightarrow f (- x) = - \sin (- x) = \sin x$

$\Rightarrow f (- x) \neq f (x)$

+ Đáp án B sai vì

$f (x) = \tan (x - \frac{π}{2}) = - \cot x$

$\Rightarrow f (- x) = - \cot (- x) = \cot x$

$\Rightarrow f (- x) \neq f (x)$

+ Đáp án D sai vì

$f (- x) = \cot (- x) = - \cot x$

$\Rightarrow f (- x) \neq f (x)$

+ Đáp án C đúng vì

$f (- x) = \sin ({(- x)}^{2} - \frac{π}{2})$

$= \sin (x^{2} - \frac{π}{2})$

$\Rightarrow f (- x) = f (x)$

Câu 31: Trong các hàm số sau, hàm số nào không là hàm chẵn và cũng không là hàm lẻ?

A. y = tanx - 1/sinx.

B. y = √2 sin(x - π/4).

C. y = sinx + tanx.

D. y = sin⁴x – cos⁴x.

Hiển thị đáp án

Đáp án: B

Giải thích:

Xét phương án B:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Do đó, hàm số đã cho không là hàm chẵn và cũng không phải là hàm lẻ

Câu 32: Hàm số y = (sinx + cosx)² + cos2x có giá trị lớn nhất là:

A. 1+√2

B. 3

C. 5

D. √2

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Suy ra hàm số có giá trị lớn nhất là 1 + √2

Câu 33: Hàm số y = √3sinx – cosx có giá trị nhỏ nhất là:

A. 1 – √3

B. - √3

C. – 2

D. – 1 – √3

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 34: Cho hàm số y = (cosx-1)/(cosx+2). Mệnh đề nào trong số các mệnh đề sau đây là sai?

A. Tập xác định của hàm số là ℝ.

B. Hàm số có giá trị lớn nhất bằng 0.

C. Hàm số có giá trị nhỏ nhất bằng - 2.

D. Hàm số tuần hoàn với chu kì T = 2.

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 35: Hàm số nào sau đây có giá trị lớn nhất bằng 2?

A. y = tanx – cotx

B. y = 2tanx

C. y = √2(cosx – sinx)

D. y = sin(2x - π/4)

Hiển thị đáp án

Đáp án: C

Giải thích:

Các hàm số y= tanx- cotx và y= 2tanx không có giá trị lớn nhất, hàm số y= sin(2x-π/4) có giá trị lớn nhất là 1. Cũng có thể nhận ngay ra đáp án C vì :

Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 36: Giá trị nhỏ nhất của hàm số y = 3- 4sin²xcos²x là:

A. – 1

B. 2

C. 1

D. 3

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 37: Hàm số y = √(1-cos2x) có chu kì là:

A. 2π

B. √2π

C. π

D. √π

Hiển thị đáp án

Đáp án: C

Giải thích:

Tập xác định của hàm số đã cho là R mà cos2x có chu kì là π nên y= √(1-cos2x) cũng có chu kì là π

Chọn đáp án C

Câu 38: Hai hàm số nào sau đây có chu kì khác nhau?

A. cos(x/2) và sin(x/2).

B. sinx và tanx.

C. cosx và cot(x/2).

D. tan2x và cot2x.

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số sinx có chu kì là 2π, hàm số tanx có chu kì là π

Vậy hai hàm số y = sinx và y = tan x có chu kì khác nhau.

Chọn đáp án B

Câu 39: Chu kì của hàm số y = 2sin(2x + π/3) -3cos(2x - π/4) là:

A. 2π

B. π

C. π/2

D. 4 π

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 40: Chu kì của hàm số y = sin2x -2cos3x là:

A. 2π

B. π

C. (2π)/3

D. π/3

Hiển thị đáp án

Đáp án: A

Giải thích:

Chu kì của hàm số y=sin2x là π, chu kì của hàm số y=cos3x là (2π)/3 nên chu kì của hàm số đã cho là 2π

Chọn đáp án A

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Phương trình lượng giác cơ bản có đáp án

Trắc nghiệm Một số phương trình lượng giác thường gặp có đáp án

Trắc nghiệm Ôn tập chương 1 có đáp án

Trắc nghiệm Quy tắc đếm có đáp án

Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp có đáp án

1 4,810 12/01/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3