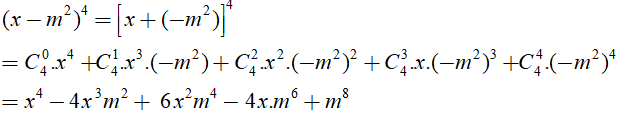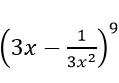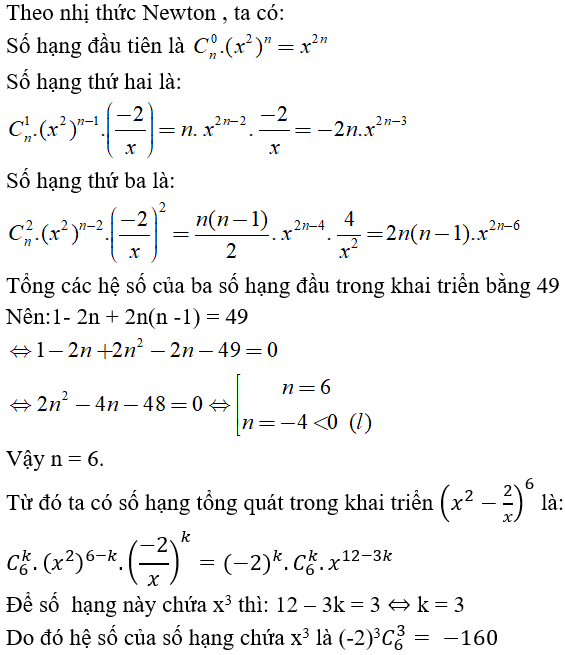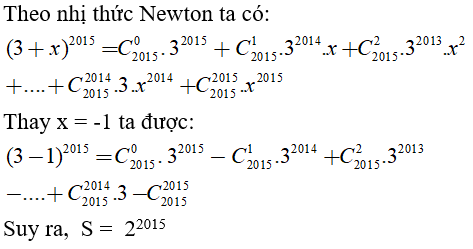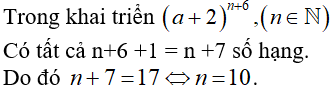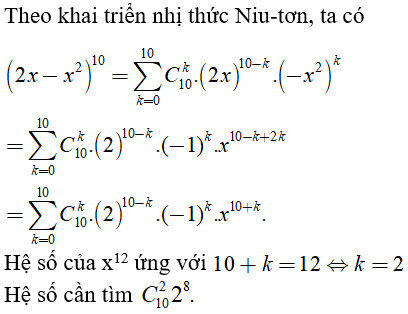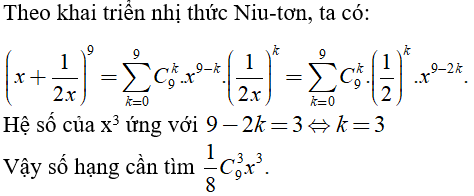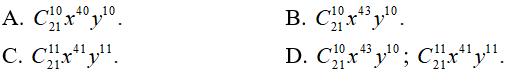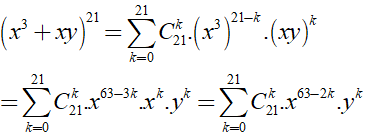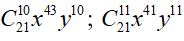TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án 2023) | Toán 11

Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 3: Nhị Thức Newton có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 3.

1 6,843 12/01/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 11 Bài 3: Nhị Thức Newton

Bài giảng Trắc nghiệm Toán 11 Bài 3: Nhị Thức Newton

Câu 1: Trong khai triển ${(3 x^{2} - y)}^{10}$ , hệ số của số hạng chính giữa là:

A. $3^{4} . C_{10}^{4}$

B. $- 3^{4} . C_{10}^{4}$

C. $3^{5} . C_{10}^{5}$

D. $- 3^{5} . C_{10}^{5}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Trong khai triển ${(3 x^{2} - y)}^{10}$ có tất cả 11 số hạng nên số hạng chính giữa là số hạng thứ .

Vậy hệ số của số hạng chính giữa là $- 3^{5} . C_{10}^{5}$ .

Câu 2: Trong khai triển ${(2 x - 5 y)}^{8}$ , hệ số của số hạng chứa $x^{5} . y^{3}$ là:

A. $- 22400$

B. $- 40000$

C. -8960

D. -4000

Hiển thị đáp án

Đáp án: A

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = {(- 1)}^{k} C_{8}^{k} . {(2 x)}^{8 - k} {(5 y)}^{k}$

$= {(- 1)}^{k} C_{8}^{k} {.2}^{8 - k} 5^{k} . x^{8 - k} . y^{k}$

Yêu cầu bài toán xảy ra khi . Khi đó hệ số của số hạng chứa $x^{5} . y^{3}$ là: $- 22400$ .

Câu 3: Trong khai triển ${(2 a - b)}^{5}$ , hệ số của số hạng thứ 3 bằng:

A. -80

B. 80

C. -10

D. 10

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: ${(2 a - b)}^{5}$

$= C_{5}^{0} {(2 a)}^{5} - C_{5}^{1} {(2 a)}^{4} b + C_{5}^{2} {(2 a)}^{3} b^{2} \dots$

Do đó hệ số của số hạng thứ 3 bằng $C_{5}^{2} .8 = 80$ .

Câu 4: Trong khai triển nhị thức ${(a + 2)}^{n + 6}, (n \in ℕ)$ . Có tất cả 17 số hạng. Vậy n bằng:

A. 17

B. 11

C. 10

D. 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Trong khai triển ${(a + 2)}^{n + 6}, (n \in ℕ)$ có tất cả n + 7 số hạng.

Do đó $n + 7 = 17 \Leftrightarrow n = 10$ .

Câu 5: Trong khai triển ${(x + \frac{2}{\sqrt[]{x}})}^{6}$ , hệ số của $x^{3}, (x > 0)$ là:

A. 60

B. 80

C. 160

D. 240

Hiển thị đáp án

Đáp án: C

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{6}^{k} . x^{6 - k} 2^{k} . x^{- \frac{1}{2} k}$

Yêu cầu bài toán xảy ra khi

$6 - k - \frac{1}{2} k = 3 \Leftrightarrow k = 3$ .

Khi đó hệ số của $x^{3}$ là: $C_{6}^{3} {.2}^{3} = 160$ .

Câu 6: Trong khai triển ${(a^{2} + \frac{1}{b})}^{7}$ , số hạng thứ 5 là:

A. $35. a^{6} . b^{- 4}$

B. $- 35. a^{6} . b^{- 4}$

C. $35. a^{4} . b^{- 5}$

D. $- 35. a^{4} . b$

Hiển thị đáp án

Đáp án: A

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{7}^{k} . a^{14 - 2 k} . b^{- k}$

Vậy số hạng thứ 5 là

$T_{5} = C_{7}^{4} . a^{6} . b^{- 4} = 35. a^{6} . b^{- 4}$

Câu 7: Trong khai triển ${(2 a - 1)}^{6}$ , tổng ba số hạng đầu là:

A. $2 a^{6} - 6 a^{5} + 15 a^{4}$

B. $2 a^{6} - 15 a^{5} + 30 a^{4}$

C. $64 a^{6} - 192 a^{5} + 480 a^{4}$

D. $64 a^{6} - 192 a^{5} + 240 a^{4}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

${(2 a - 1)}^{6}$

$= C_{6}^{0} {.2}^{6} a^{6} - C_{6}^{1} {.2}^{5} a^{5} + C_{6}^{2} {.2}^{4} a^{4} - ...$

Vậy tổng 3 số hạng đầu là $64 a^{6} - 192 a^{5} + 240 a^{4}$ .

Câu 8: Trong khai triển ${(x + \frac{8}{x^{2}})}^{9}$ , số hạng không chứa x là:

A. 4308

B. 86016

C. 84

D. $43008$

Hiển thị đáp án

Đáp án: D

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{9}^{k} . x^{9 - k} 8^{k} . x^{- 2 k}$

Yêu cầu bài toán xảy ra khi

$9 - k - 2 k = 0 \Leftrightarrow k = 3$ .

Khi đó số hạng không chứa x là: $C_{9}^{3} {.8}^{3} = 43008$ .

Câu 9: Trong khai triển ${(2 x - 1)}^{10}$ , hệ số của số hạng chứa $x^{8}$ là:

A. -11520

B. 45

C. 256

D. 11520

Hiển thị đáp án

Đáp án: D

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{10}^{k} {.2}^{10 - k} . x^{10 - k} . {(- 1)}^{k}$

Yêu cầu bài toán xảy ra khi

$10 - k = 8 \Leftrightarrow k = 2$ .

Khi đó hệ số của số hạng chứa $x^{8}$ là: $C_{10}^{2} {.2}^{8} = 11520$ .

Câu 10: Trong khai triển ${(a - 2 b)}^{8}$ , hệ số của số hạng chứa $a^{4} . b^{4}$ là:

A. 1120

B. 560

C. 140

D. 70

Hiển thị đáp án

Đáp án: A

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{8}^{k} . a^{8 - k} . {(- 2)}^{k} . b^{k}$

Yêu cầu bài toán xảy ra khi k = 4.

Khi đó hệ số của số hạng chứa $a^{4} . b^{4}$ là: $C_{8}^{4} {.2}^{4} = 1120$ .

Câu 11: Trong khai triển ${(3 x - y)}^{7}$ , số hạng chứa $x^{4} y^{3}$ là:

A. $- 2835 x^{4} y^{3}$

B. $2835 x^{4} y^{3}$

C. $945 x^{4} y^{3}$

D. $- 945 x^{4} y^{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{7}^{k} {.3}^{7 - k} x^{7 - k} . {(- 1)}^{k} . y^{k}$

Yêu cầu bài toán xảy ra khi k = 3 .

Khi đó hệ số của số hạng chứa $x^{4} . y^{3}$ là:

$- C_{7}^{3} {.3}^{4} . x^{4} . y^{3} = - 2835. x^{4} . y$ .

Câu 12: Trong khai triển ${(0,2 + 0,8)}^{5}$ , số hạng thứ tư là:

A. 0,0064

B. 0,4096

C. 0,0512

D. 0,2048

Hiển thị đáp án

Đáp án: D

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{5}^{k} . {(0, 2)}^{5 - k} . {(0, 8)}^{k}$

Vậy số hạng thứ tư là

$T_{4} = C_{5}^{3} . {(0, 2)}^{2} . {(0, 8)}^{3} = 0, 2028$

Câu 13: Trong khai triển ${(x - \sqrt{y})}^{16}$ , tổng hai số hạng cuối là:

A. $- 16 x \sqrt{y^{15}} + y^{8}$

B. $- 16 x \sqrt{y^{15}} + y^{4}$

C. $16 x y^{15} + y^{4}$

D. $16 x y^{15} + y^{8}$

Hiển thị đáp án

Đáp án: A

Câu 14: Tính tổng sau:

$S = C_{n}^{1} 3^{n - 1} + 2 C_{n}^{2} 3^{n - 2} + ... + n C_{n}^{n}$

A. $n {.4}^{n - 1}$

B. 0

C. 1

D. $4^{n - 1}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $S = 3^{n} \sum_{k = 1}^{n} k C_{n}^{k} {(\frac{1}{3})}^{k}$

Vì $k C_{n}^{k} {(\frac{1}{3})}^{k} = n {(\frac{1}{3})}^{k} C_{n - 1}^{k - 1}$ nên

$S = 3^{n} . n \sum_{k = 1}^{n} {(\frac{1}{3})}^{k} C_{n - 1}^{k - 1}$

$= 3^{n - 1} . n \sum_{k = 0}^{n - 1} {(\frac{1}{3})}^{k} C_{n - 1}^{k}$ .

Câu 15: Trong khai triển ${(8 a^{2} - \frac{1}{2} b)}^{6}$ , hệ số của số hạng chứa $a^{9} b^{3}$ là:

A. $- 80 a^{9} . b^{3}$

B. $- 64 a^{9} . b^{3}$

C. $- 1280 a^{9} . b^{3}$

D. $60 a^{6} . b^{4}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = {(- 1)}^{k} C_{6}^{k} {.8}^{6 - k} a^{12 - 2 k} {.2}^{- k} b^{k}$

Yêu cầu bài toán xảy ra khi k = 3 .

Khi đó hệ số của số hạng chứa $a^{9} b^{3}$ là: $- 1280 a^{9} . b^{3}$ .

Câu 16: Hệ số của $x^{3} y^{3}$ trong khai triển ${(1 + x)}^{6} {(1 + y)}^{6}$ là:

A. 20

B. 800

C. 36

D. 400

Hiển thị đáp án

Đáp án: D

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{6}^{k} . x^{k} . C_{6}^{m} . y^{m}$

Yêu cầu bài toán xảy ra khi k = m = 3 .

Khi đó hệ số của số hạng chứa $x^{3} y^{3}$ là: $C_{6}^{3} . C_{6}^{3} = 400$ .

Câu 17: Số hạng chính giữa trong khai triển ${(3 x + 2 y)}^{4}$ là:

A. $C_{4}^{2} x^{2} y^{2}$

B. $6 {(3 x)}^{2} {(2 y)}^{2}$

C. $6 C_{4}^{2} x^{2} y^{2}$

D. $36 C_{4}^{2} x^{2} y^{2}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Số hạng chính giữa trong khai triển trên là số hạng thứ ba:

$C_{4}^{2} {(3 x)}^{2} {(2 y)}^{2} = 6 {(3 x)}^{2} {(2 y)}^{2}$ .

Câu 18: Trong khai triển ${(x - y)}^{11}$ , hệ số của số hạng chứa $x^{8} . y^{3}$ là

A. $C_{11}^{3}$

B. $- C_{11}^{3}$

C. $- C_{11}^{5}$

D. $C_{11}^{8}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Số hạng tổng quát trong khai triển trên là

$T_{k + 1} = C_{11}^{k} . x^{11 - k} . {(- 1)}^{k} . y^{k}$

Yêu cầu bài toán xảy ra khi k = 3.

Khi đó hệ số của số hạng chứa $x^{8} . y^{3}$ là: $- C_{11}^{3}$ .

Câu 19: Tìm hệ số của $x^{7}$ trong khai triển thành đa thức của ${(2 - 3 x)}^{2 n}$ , biết n là số nguyên dương thỏa mãn: $C_{2 n + 1}^{1} + C_{2 n + 1}^{3} + ... + C_{2 n + 1}^{2 n + 1} = 1024$ .

A. 2099529

B. -2099520

C. -2099529

D. 2099520

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$\{\begin{cases} \sum_{k = 0}^{2 n + 1} C_{2 n + 1}^{k} = 2^{2 n + 1} \\ \sum_{i = 0}^{n} C_{2 n + 1}^{2 i + 1} = \sum_{i = 0}^{n} C_{2 n + 1}^{2 i} \end{cases}$

$\Rightarrow \sum_{i = 0}^{n} C_{2 n + 1}^{2 i + 1} = 2^{2 n} = 1024$

$\Rightarrow n = 5$

Suy ra :

${(2 - 3 x)}^{2 n}$

$= \sum_{k = 0}^{10} C_{10}^{k} 2^{10 - k} . {(- 3)}^{k} x^{k}$

Hệ số của $x^{7}$ là

$C_{10}^{7} {.2}^{3} . {(- 3)}^{7} = - 2099520$ .

Câu 20: Tìm hệ số của $x^{9}$ trong khai triển

$f (x) = {(1 + x)}^{9} + ... + {(1 + x)}^{14}$

A. 8089

B. 8085

C. 3003

D. 11312

Hiển thị đáp án

Đáp án: C

Giải thích:

Hệ số của :

$C_{9}^{9} + C_{10}^{9} + C_{11}^{9} + C_{12}^{9} + C_{13}^{9} + C_{14}^{9}$

$= 3003$ .

Câu 21: Tìm hệ số của $x^{5}$ trong khai triển đa thức của $x {(1 - 2 x)}^{5} + x^{2} {(1 + 3 x)}^{10}$ :

A. 3320

B. 2130

C. 3210

D. 1313

Hiển thị đáp án

Đáp án: A

Giải thích:

Đặt $f (x) = x {(1 - 2 x)}^{5} + x^{2} {(1 + 3 x)}^{10}$

Ta có :

$f (x)$

$= x \sum_{k = 0}^{5} C_{5}^{k} {(- 2)}^{k} . x^{k}$

$+ x^{2} \sum_{i = 0}^{10} C_{10}^{i} {(3 x)}^{i}$

$= \sum_{k = 0}^{5} C_{5}^{k} {(- 2)}^{k} . x^{k + 1}$

$+ \sum_{i = 0}^{10} C_{10}^{i} 3^{i} . x^{i + 2}$

Vậy hệ số của $x^{5}$ trong khai triển đa thức của $f (x)$ ứng với k = 4 và i = 3 là:

$C_{5}^{4} {(- 2)}^{4} + C_{10}^{3} {.3}^{3} = 3320$ .

Câu 22: Tính tổng sau: $S = \frac{1}{2} C_{n}^{0} - \frac{1}{4} C_{n}^{1} + ... + \frac{{(- 1)}^{n}}{2 (n + 1)} C_{n}^{n}$

A. $\frac{1}{2 (n + 1)}$

B. 1

C. 2

D. $\frac{1}{(n + 1)}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$S = \frac{1}{2} (C_{n}^{0} - \frac{1}{2} C_{n}^{1} + ... + \frac{{(- 1)}^{n}}{n + 1} C_{n}^{n})$

Vì $\frac{{(- 1)}^{k}}{k + 1} C_{n}^{k} = \frac{{(- 1)}^{k}}{n + 1} C_{n + 1}^{k + 1}$ nên:

$S = \frac{1}{2 (n + 1)} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n + 1}^{k + 1}$

$= \frac{- 1}{2 (n + 1)} (\sum_{k = 0}^{n + 1} {(- 1)}^{k} C_{n + 1}^{k} - C_{n + 1}^{0})$

$= \frac{1}{2 (n + 1)}$ .

Câu 23: Tổng $T = C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + C_{n}^{3} + ... + C_{n}^{n}$ bằng:

A. $T = 2^{n}$

B. $T = 2^{n} - 1$

C. $T = 2^{n} + 1$

D. $T = 4^{n}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Tính chất của khai triển nhị thức Niu – Tơn.

Câu 24: Tính giá trị của tổng $S = C_{6}^{0} + C_{6}^{1} + .. + C_{6}^{6}$ bằng:

A. 64

B. 48

C. 72

D. 100

Hiển thị đáp án

Đáp án: A

Giải thích:

${S = C}_{6}^{0} {+C}_{6}^{1} + ... {+C}_{6}^{6} = 2^{6} = 64$

Câu 25: Khai triển ${(x + y)}^{5}$ rồi thay x , y bởi các giá trị thích hợp. Tính tổng

$S = C_{5}^{0} + C_{5}^{1} + ... + C_{5}^{5}$

A. 32

B. 64

C. 1

D. 5

Hiển thị đáp án

Đáp án: A

Giải thích:

Với $x = 1, y = 1$ ta có

${S= C}_{5}^{0} {+C}_{5}^{1} + ... {+C}_{5}^{5} = {(1 + 1)}^{5} = 32$ .

Câu 26: Tìm hệ số của $x^{7}$ trong khai triển biểu thức sau:

$f (x) = {(1 - 2 x)}^{10}$

A. -15360

B. 15360

C. -15363

D. 15363

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $f (x) = \sum_{k = 0}^{10} C_{n}^{k} 1^{10 - k} {(- 2 x)}^{k}$

$= \sum_{k = 0}^{10} C_{10}^{k} {(- 2)}^{k} x^{k}$

Số hạng chứa $x^{7}$ ứng với giá trị k = 7 .

Vậy hệ số của $x^{7}$ là: $C_{10}^{7} {(- 2)}^{7} = - 15360$ .

Câu 27: Tìm hệ số của $x^{7}$ trong khai triển biểu thức sau: $h (x) = x {(2 + 3 x)}^{9}$

A. 489889

B. 489887

C. -489888

D. 489888

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có ${(2 + 3 x)}^{9} = \sum_{k = 0}^{9} C_{9}^{k} 2^{9 - k} {(3 x)}^{k}$

$= \sum_{k = 0}^{9} C_{9}^{k} 2^{9 - k} 3^{k} . x^{k}$

$\Rightarrow h (x) = \sum_{k = 0}^{9} C_{9}^{k} 2^{9 - k} 3^{k} x^{k + 1}$ .

Số hạng chứa $x^{7}$ ứng với giá trị k thỏa $k + 1 = 7 \Leftrightarrow k = 6$

Vậy hệ số chứa $x^{7}$ là: $C_{9}^{6} 2^{3} 3^{6} = 489888$ .

Câu 28: Tìm hệ số của $x^{7}$ trong khai triển biểu thức sau:

$g (x) = {(1 + x)}^{7} + {(1 - x)}^{8} + {(2 + x)}^{9}$

A. 29

B. 30

C. 31

D. 32

Hiển thị đáp án

Đáp án: A

Giải thích:

Hệ số của $x^{7}$ trong khai triển ${(1 + x)}^{7} = \sum_{k = 0}^{7} C_{7}^{k} x^{k}$ là : $C_{7}^{7} = 1$

Hệ số của $x^{7}$ trong khai triển ${(1 - x)}^{8} = \sum_{k = 0}^{8} C_{8}^{k} {(- 1)}^{k} x^{k}$ là : $C_{8}^{7} {(- 1)}^{7} = - 8$

Hệ số của $x^{7}$ trong khai triển ${(1 + x)}^{9} = \sum_{k = 0}^{9} C_{9}^{k} x^{k}$ là : $C_{7}^{9} = 36$ .

Vậy hệ số chứa $x^{7}$ trong khai triển $g (x)$ thành đa thức là: 29.

Chú ý:

* Với $a \neq 0$ ta có: $a^{- n} = \frac{1}{a^{n}}$ với $n \in ℕ$ .

* Với $a \geq 0$ ta có: $\sqrt[n]{a^{m}} = a^{\frac{m}{n}}$ với $m, n \in ℕ; n \geq 1$ .

Câu 29: Tính các tổng sau:

$S_{3} = 2.1. C_{n}^{2} + 3.2 C_{n}^{3} + ... + n (n - 1) C_{n}^{n}$ .

A. $n (n - 1) 2^{n - 2}$

B. $n (n + 2) 2^{n - 2}$

C. $n (n - 1) 2^{n - 3}$

D. $n (n - 1) 2^{n + 2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $k (k - 1) C_{n}^{k}$

$= \frac{n!}{(k - 2)! (n - k)!}$

$= n (n - 1) C_{n - 2}^{k - 2}$

$\Rightarrow S_{3} = n (n - 1) \sum_{k = 2}^{n} C_{n - 2}^{k - 2}$

$= n (n - 1) 2^{n - 2}$ .

Câu 30: Tính tổng $S = C_{n}^{0} + \frac{3^{2} - 1}{2} C_{n}^{1} + ... + \frac{3^{n + 1} - 1}{n + 1} C_{n}^{n}$

A. $S = \frac{4^{n + 1} - 2^{n + 1}}{n + 1}$

B. $S = \frac{4^{n + 1} + 2^{n + 1}}{n + 1} - 1$

C. $S = \frac{4^{n + 1} - 2^{n + 1}}{n + 1} + 1$

D. $S = \frac{4^{n + 1} - 2^{n + 1}}{n + 1} - 1$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $S = S_{1} - S_{2}$ , trong đó

$S_{1} = C_{n}^{0} + \frac{3^{2}}{2} C_{n}^{1} + ... + \frac{3^{n + 1}}{n + 1} C_{n}^{n}$

$S_{2} = \frac{1}{2} C_{n}^{1} + \frac{1}{3} C_{n}^{2} + ... + \frac{1}{n + 1} C_{n}^{n}$

Ta có $S_{2} = \frac{2^{n + 1} - 1}{n + 1} - 1$

Tính $S_{1} = ?$

Ta có: $\frac{3^{k + 1}}{k + 1} C_{n}^{k} = 3^{k + 1} \frac{n!}{(k + 1)! (n - k)!}$

$= \frac{3^{k + 1}}{n + 1} \frac{(n + 1)!}{(k + 1)! [(n + 1) - (k + 1)]!}$

$= \frac{3^{k + 1}}{n + 1} C_{n + 1}^{k + 1}$

$\Rightarrow S_{1} = \frac{1}{n + 1} \sum_{k = 0}^{n} 3^{k + 1} C_{n + 2}^{k + 1} - 2 C_{n}^{0}$

$= \frac{1}{n + 1} (\sum_{k = 0}^{n + 1} 3^{k} C_{n + 1}^{k} - C_{n}^{0}) - 2 C_{n}^{0}$

$= \frac{4^{n + 1} - 1}{n + 1} - 2$ .

Vậy $S = \frac{4^{n + 1} - 2^{n + 1}}{n + 1} - 1$ .

Câu 31. Khai triển biểu thức (x-m²)⁴ thành tổng các đơn thức:

A. x⁴ –x³m+x²m² + m⁴

B. x⁴ –x³m²+x²m⁴ –xm⁶+ m⁸

C. x⁴ –4x³m+6x²m² -4xm+ m⁴

D. x⁴ –4x³m²+6x²m⁴ – 4xm⁶+ m⁸

Hiển thị đáp án

Đáp án: D

Giải thích:

Sử dụng nhị thức Niuton với a = x, b = - m²

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 32. Tìm số hạng không chứa x trong khai triển Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

A. 2268

B. -2268

C. 84

D. -27

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 33. Xác định hệ số của số hạng chứa x3 trong khai triển (x²-2/x)ⁿ nếu biết tổng các hệ số của ba số hạng đầu trong khai triển đó bằng 49.

A. 160

B. -160

C. 160x³

D. -160x³

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 34. Tính tổng S = 3²⁰¹⁵.C₂₀₁₅-3²⁰¹⁴.C₂₀₁₅¹+3²⁰¹³.C₂₀₁₅²-…+3C₂₀₁₅²⁰¹⁴ -C₂₀₁₅²⁰¹⁵

A. 22015

B. -22015

C. 32015

D. 42015

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 35. Trong khai triển nhị thức (a + 2)^{n + 6}, (n ∈ N). Có tất cả 17 số hạng. Vậy n bằng:

A. 17

B. 11

C. 10

D. 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 36. Tìm hệ số của x¹² trong khai triển (2x - x²)¹⁰

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 37. Tìm số hạng chứa x³ trong khai triển Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 38. Tìm số hạng đứng giữa trong khai triển (x³+ xy)²¹

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Hiển thị đáp án

Đáp án: D

Giải thích:

Theo khai triển nhị thức Niu-tơn, ta có

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Suy ra khai triển (x³+ xy)²¹ có 22 số hạng nên có hai số hạng đứng giữa là số hạng thứ 11 (ứng với k = 10) và số hạng thứ 12 (ứng với k = 11). Vậy hai số hạng đứng giữa cần tìm là

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 39. Tìm hệ số của x⁵ trong khai triển P(x) = x(1 - 2x)⁵ + x²(1 + 3x)¹⁰

A. 80

B. 3240

C. 3320

D. 259200

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Câu 40. Tìm hệ số của x5 trong khai triển : P(x) = (1 + x) + 2(1 + x)² + ... + 8(1 + x)⁸.

A. 630

B. 635

C. 636

D.637

Hiển thị đáp án

Đáp án: C

Giải thích:

Các biểu thức (1 + x), (1 + x)², ⋯, (1 + x)⁴ không chứa số hạng chứa x⁵.

Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:

Trắc nghiệm Phép thử và Biến cố có đáp án

Trắc nghiệm Xác suất của biến cố có đáp án

Trắc nghiệm Ôn tập chương 2 có đáp án

Trắc nghiệm Phương pháp quy nạp toán học có đáp án

Trắc nghiệm Dãy số có đáp án

1 6,843 12/01/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3