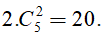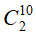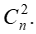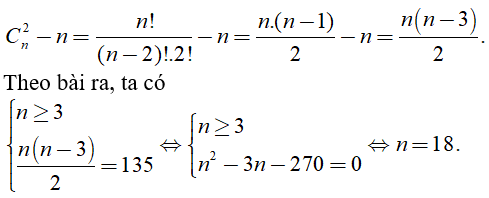TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án 2023) – Toán 11
Bộ 40 câu hỏi trắc nghiệm Toán lớp 11 Bài 2: Hoán Vị - Chỉnh Hợp – Tổ Hợp có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 11 Bài 2.
Trắc nghiệm Toán 11 Bài 2: Hoán Vị - Chỉnh Hợp – Tổ Hợp
Bài giảng Trắc nghiệm Toán 11 Bài 2: Hoán Vị - Chỉnh Hợp – Tổ Hợp
Câu 1. Cho . Số hoán vị của ba phần tử của A là:
A. 4
B. 5
C. 6
D. 7
Đáp án: C
Giải thích:
Số hoán vị của ba phần tử của A là 3! = 6.
Câu 2. Một lớp học có 30 học sinh, trong đó có 18 em giỏi Toán, 14 em giỏi văn và 10 em không giỏi môn nào. Số tất cả các em giỏi cả văn lẫn toán là:
A. 20
B. 12
C. 24
D. 48
Đáp án: B
Giải thích:
Số học sinh giỏi ít nhất 1 môn là:
30 – 10 = 20
Số học sinh giỏi cả văn lẫn toán là:
18 + 14 – 20 = 12.
Câu 3. Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
A. 60
B. 180
C. 330
D. 90
Đáp án: A
Giải thích:
Chọn 3 học sinh lớp 12 có cách, chọn 1 học sinh lớp 11 có cách, chọn 1 học sinh lớp 10 có cách. Do đó có cách chọn.
Câu 4. Số hoán vị của n phần tử là:
A.
B.
C.
D.
Đáp án: D
Giải thích:
Số hoán vị của n phần tử là
Câu 5. Có bao nhiêu số có 4 chữ số khác nhau được tạo thành từ các số 1, 2, 3, 4, 5?
A.
B.
C.
D.
Đáp án: C
Giải thích:
Số có 4 chữ số khác nhau tạo thành từ tập trên là .
Câu 6. Cho với . Mệnh đề nào có giá trị sai?
A.
B.
C.
D.
Đáp án: A
Giải thích:
Ta có nên A sai.
Câu 7. Từ 6 chữ số 0, 1, 2, 3, 4, 5 ta lập được bao nhiêu số chẵn, mỗi số gồm 5 chữ số khác nhau?
A. 120
B. 192
C. 312
D. 216
Đáp án: C
Giải thích:
Giả sử số đó là .
Trường hợp 1: chọn có cách có số thỏa mãn
Trường hợp 2: chọn có 4 cách chọn, chọn có cách có cách
Do đó có số thỏa mãn.
Câu 8. Có 18 đội bóng đá tham gia thi đấu. Mỗi đội chỉ có thể nhận nhiều nhất là một huy chương và đội nào cũng có thể đoạt huy chương. Khi đó, số cách trao 3 loại huy chương vàng, bạc, đồng cho ba đội nhất nhì ba là:
A. 51
B. 4896
C. 125
D. 12070
Đáp án: B
Giải thích:
Ta có 3 đội bất kì trong 18 đội đều có khả năng đạt huy chương, và thứ tự của 3 đội này sẽ cho biết loại huy chương mà mỗi đội nhận, đo đó số cách trao cần tìm: .
Câu 9. Cho số . M có tất cả bao nhiêu ước số dương?
A. 60
B. 13
C. 140
D. 120
Đáp án: D
Giải thích:
Số ước dương là: .
Câu 10. Có bao nhiêu số là ước dương của và chia hết cho ?
A. 30
B. 150
C. 60
D. 120
Đáp án: B
Giải thích:
Để ý rằng .
Với mỗi ước dương của khi nhân với đều là ước dương của thỏa mãn yêu cầu đề. Số ước dương cần tìm là: .
Câu 11. Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu?
A. 18
B. 9
C. 22
D. 4
Đáp án: B
Giải thích:
Số cách lấy hai viên bi cùng màu đỏ là .
Số cách lấy hai viên bi cùng màu xanh là .
Như vậy số cách lấy dc hai viên bi cùng màu là cách.
Câu 12. Một tổ học sinh có 5 nam và 5 nữ xếp thành 1 hàng dọc sao cho không có học sinh cùng giới tính đứng kề nhau. Số cách xếp là:
A. 5!.5!
B. 2.(5!)2
C. 10!
D. 2.5!
Đáp án: B
Giải thích:
Theo bài ra, ta thấy cách sắp xếp chính là việc nam nữ đứng xen kẽ nhau.
Như vậy sẽ có hai trường hợp, hoặc là bạn nam đứng đầu hàng hoặc là bạn nữ đứng đầu hàng.
Và 5 bạn nam thay đổi vị trí cho nhau tương ứng với 5! cách.
Tương tự với 5 bạn nữ thay đổi vị trí tương ứng với 5! cách.
Vậy số cách sắp xếp cần tìm .
Câu 13. Cho 5 chữ số 0, 1, 2, 3, 4. Có bao nhiêu số gồm 5 chữ số khác nhau được tạo thành từ 5 chữ số trên?
A. 120
B. 96
C. 24
D. 28
Đáp án: B
Giải thích:
Gọi số cần tìm có dạng , khi đó
+) Có 4 cách chọn chữ số a (trừ chữ số 0).
+) Có 4 cách chọn chữ số b.
+) Có 3 cách chọn chữ số c.
+) Có 2 cách chọn chữ số d.
+) Có 1 cách chọn chữ số e.
Vậy có tất cả 4.4.3.2.1 = 96 số cần tìm.
Câu 14. Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 9?
A. 16
B. 18
C. 20
D. 14
Đáp án: A
Giải thích:
Gọi số cần tìm có dạng với .
Vì nên suy ra tổng các chữ số .
Khi đó .
TH1. Với suy ra có 2.2 = 4 số thỏa mãn yêu cầu.
TH2. Với suy ra có 3! = 6 số thỏa mãn yêu cầu.
TH3. Với suy ra có 3! = 6 số thỏa mãn yêu cầu.
Vậy có thể lập được 16 số tự nhiên thỏa mãn bài toán.
Câu 15. Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?
A. 120
B. 60
C. 30
D. 40
Đáp án: A
Giải thích:
Số có 5 chữ số khác nhau dc tạo thành từ tập trên là 5! = 120.
Câu 16. Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:
A. 25
B. 10
C. 10!
D. 40
Đáp án: C
Giải thích:
Số cách xếp là 10!.
Câu 17. Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này, ta lập các số chẵn có 5 chữ số khác nhau. Số các số có thể lập được là:
A. 120
B. 48
C. 32
D. 40
Đáp án: B
Giải thích:
Giả sử số đó là . Chọn có 2 cách, chọn có 4! cách
Do đó có số thỏa mãn.
Câu 18. Dũng có 8 người bạn. Dũng muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối tuần. Nhưng trong 8 người bạn đó, có 2 bạn là Hùng và Tuấn không thích đi chơi với nhau. Như vậy số cách chọn nhóm 4 người để về quê của Dũng là?
A.
B.
C.
D.
Đáp án: C
Giải thích:
TH1. Trong 4 bạn được mời, có Hùng nhưng không có Tuấn.
Số cách chọn nhóm 4 người trong trường hợp này là cách.
TH2. Tương tự TH1, có Tuấn nhưng không có Hùng nên số cách chọn là cách.
TH3. Trong 4 bạn được mời, không có cả Hùng và Tuấn.
Số cách chọn nhóm 4 người trong trường hợp này là cách.
Vậy số cách chọn cần tìm là cách.
Câu 19. Một tổ có 6 học sinh, trong đó có 3 học sinh nam và 3 học sinh nữ. Hỏi có bao nhiêu cách xếp các học sinh trong tổ thành một hàng dọc sao cho nam, nữ đứng xen kẽ nhau?
A. 36
B. 42
C. 102
D. 72
Đáp án: D
Giải thích:
Ta xét hai trường hợp:
TH1. Bạn nam đứng đầu hàng, khi đó số cách sắp xếp là 3.2.3! = 36 cách.
TH2. Bạn nữ đứng đầu hàng, tương tự TH1, suy ra có 36 cách sắp xếp.
Vậy có 72 cách sắp xếp thỏa mãn yêu cầu bài toán.
Câu 20. Hai đơn vị thi đấu cờ tướng A và B lần lượt có 5 người và 6 người. Cần chọn ra mỗi đơn vị 3 người để ghép cặp thi đấu với nhau. Hỏi có bao nhiêu cách thực hiện như thế?
A. 1200
B.
C.
D.
Đáp án: A
Giải thích:
Số cách chọn 3 người từ đơn vị A là cách.
Số cách chọn 3 người từ đơn vị B là cách.
Lấy 1 người trong đơn vị A đi ghép cặp đấu với 1 trong 3 người ở đơn vị B, ta được 3 cách.
Lấy 1 người trong 2 người còn lại ở đơn vị A đi ghép cặp đấu với 1 trong 2 người còn lại ở đơn vị B, ta được 2 cách.
Vậy có cách thực hiện việc ghép cặp thi đấu.
Câu 21. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Hỏi có bao nhiêu cách tuyển chọn?
A. 240
B. 260
C. 126
D. Kết quả khác
Đáp án: C
Giải thích:
Số cách chọn ban quản trị gồm 1 nam và 3 nữ là cách.
Số cách chọn ban quản trị gồm 2 nam và 2 nữ là cách.
Số cách chọn ban quản trị gồm 3 nam và 1 nữ là cách.
Số cách chọn ban quản trị gồm 4 nam là cách.
Số cách chọn ban quản trị gồm 4 nữ là cách.
Vậy tổng số cách chọn cần tìm là
Câu 22. Có bao nhiêu cách chọn và sắp thứ tự 5 cầu thủ để đá bóng luân lưu 11m. Biết rằng cả 11 cầu thủ đều có khả năng như nhau.
A. 55440
B. 20680
C. 32456
D. 41380
Đáp án: A
Giải thích:
Số cách chọn 5 cầu thủ trong 11 cầu thủ và sắp xếp có thứ tự là .
Câu 23. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?
A. 240
B. 260
C. 126
D. Kết quả khác
Đáp án: D
Giải thích:
Số cách chọn ban quản trị gồm 1 nam và 3 nữ là cách.
Số cách chọn ban quản trị gồm 2 nam và 2 nữ là cách.
Số cách chọn ban quản trị gồm 3 nam và 1 nữ là cách.
Vậy tổng số cách chọn cần tìm là
cách.
Câu 24. Một lớp có 50 học sinh. Hỏi có bao nhiêu cách phân công 3 học sinh để làm vệ sinh lớp học trong một ngày?
A. 117600
B. 128500
C. 376
D. 436
Đáp án: A
Giải thích:
Số cách phân công 3 học sinh để làm vệ sinh lớp học là .
Câu 25. Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?
A. 200
B. 30
C. 300
D. 120
Đáp án: D
Giải thích:
Cố định 3 tem thư xếp theo hàng ngang từ trái sang phải là các vị trí 1, 2, 3.
Rõ ràng nếu có 3 bì thư thì mỗi thứ tự xếp 3 bì thư này từ trái sáng phải cũng chính là cách dán.
Số cách làm cần tìm là: .
Câu 26. Từ 12 người, người ta thành lập một ban kiểm tra gồm 2 người lãnh đạo và 3 ủy viên. Hỏi có bao nhiêu cách thành lập ban kiểm tra?
A.
B.
C.
D. Kết quả khác
Đáp án: A
Giải thích:
Số cách chọn 2 lãnh đạo từ 12 người đã cho:
Số cách chọn 3 ủy viên từ 10 người còn lại:
Tổng số cách thành lập ban kiểm tra: .
Câu 27. Có 4 cuốn sách toán khác nhau, 3 sách lý khác nhau, 2 sách hóa khác nhau. Muốn sắp và một kệ dài các cuốn sách cùng môn kề nhau, 2 loại toán và lý phải kề nhau thì số cách sắp là:
A. 4!.3!.2!
B. 2.4!.3!.2!
C. 3.4!.3!.2!
D. 4.4!.3!.2!
Đáp án: D
Giải thích:
Đối với 3 vị trí của 3 loại sách thì sách hóa chỉ có thể đứng ở đầu hoặc cuối: 2 cách chọn.
Tương ứng mỗi vị trí của loại sách hóa thì số cách xếp các cuốn sách hóa là: 2!
Tương tự, số cách xếp toán và lý là: 2.4!.3!
Vậy tổng số cách xếp cần tìm: 2.4!.3!.(2!.2) = 4.4!.3!.2!.
Câu 28. Từ các số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số có 7 chữ số khác nhau mà hai chữ số chẵn đứng kề nhau?
A. 6!
B. 2.6!
C. 7!
D. 2.7!
Đáp án: B
Giải thích:
Số số có 7 chữ số khác nhau lập từ các chữ số đã cho: 7!
Xếp 4 chữ số lẻ trên 1 hàng ngang với vị trí bất kì: 4! Cách.
Ở đây giữa sẽ tạo thành 5 khoảng trống (bao gồm 3 khoảng trống giữa hai chữ số lẻ và 2 khoảng trống tại vị trí đầu và cuối). Ở mỗi khoảng trống, ta sẽ điền các chữ số chẵn 2, 4, 6 vào không kể thứ tự sao cho mỗi khoảng trống chỉ có 1 chữ số chẵn:
Cách xếp này cũng chính là số số thỏa yêu cầu đề: .
Câu 29. Có 3 môn thi Toán, Lí, Hóa cần xếp vào 3 buổi thi, mỗi buổi 1 môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:
A. 3!
B. 2!
C. 3! – 2!
D. 5
Đáp án: C
Giải thích:
Số cách xếp bất kì 3 môn vào 3 buổi thi bất kì là: 3!
Giả sử môn Toán luôn thi buổi đầu, thì số cách xếp 2 môn còn lại vào bất kì 2 buổi còn lại là: 2!
Vậy số cách xếp cần tìm: 3! – 2!.
Câu 30. Có 12 tay đua xe đạp cùng xuất phát trong một cuộc đua để chọn ra 3 người về đích đầu tiên. Số kết quả có thể xảy ra là:
A. 1250
B. 1320
C. 220
D. 240
Đáp án: C
Giải thích:
Ở đây yêu cầu 3 người về đích đầu tiên, nên giữa 3 người này không cần phải phân định thứ tự nhất nhì ba. Số kết quả xảy ra là: .
Câu 31. Cho 10 điểm phân biệt A1, A2, ..., A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
A. 96 tam giác.
B. 60 tam giác.
C. 116 tam giác.
D. 80 tam giác.
Đáp án: C
Giải thích:
Số cách lấy 3 điểm từ 10 điểm phân biệt là 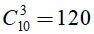
Số cách lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 là 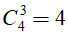
Khi lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 thì sẽ không tạo thành tam giác.
Như vậy, số tam giác tạo thành : 120 - 4 = 116 tam giác.
Câu 32. Cho hai đường thẳng song song d1 và d2. Trên d1 lấy 17 điểm phân biệt, trên d2 lầy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
A. 5690
B. 5960
C. 5950
D. 5590
Đáp án: C
Giải thích:
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d1 và 2 điểm thuộc d2: có 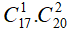
TH2. Chọn 2 điểm thuộc d1 và 1 điểm thuộc d2: có 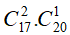
Như vậy, ta có 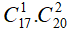
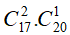
Câu 33. Số giao điểm tối đa của 5 đường tròn phân biệt là:
A. 10
B. 20
C. 18
D. 22
Đáp án: B
Giải thích:
Hai đường tròn phân biệt cho tối đa hai giao điểm.
Và 5 đường tròn phân biệt cho số giao điểm tối đa khi 2 đường tròn bất kỳ trong 5 đường tròn đôi một cắt nhau.
Vậy số giao điểm tối đa của 5 đường tròn phân biệt là
Câu 34. Với đa giác lồi 10 cạnh thì số đường chéo là
A. 90
B. 45
C. 35
D. Một số khác.
Đáp án: C
Giải thích :
Đa giác lồi 10 cạnh thì có 10 đỉnh.
Lấy hai điểm bất kỳ trong 10 đỉnh của đa giác lồi ta được số đoạn thẳng gồm cạnh và đường chéo của đa giác lồi.
Do đó, tổng số cạnh và đường chéo của đa giác là:
Suy ra,số đường chéo cần tìm là 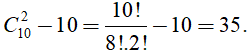
Câu 35. Cho đa giác đều n đỉnh, n ∈ N và n ≥ 3 Tìm n biết rằng đa giác đã cho có 135 đường chéo.
A. n = 15
B. n = 27
C. n = 8
D. n = 18
Đáp án: D
Giải thích:
Đa giác lồi n đỉnh thì có n cạnh.
Nếu vẽ tất cả các đoạn thẳng nối từng cặp trong n đỉnh này thì có một bộ gồm các cạnh và các đường chéo.
Vậy để tính số đường chéo thì lấy tổng số đoạn thẳng dựng được trừ đi số cạnh,
• Tất cả đoạn thẳng dựng được là bằng cách lấy ra 2 điểm bất kỳ trong n điểm, tức là số đoạn thẳng chính là số tổ hợp chập 2 của n phần tử.
Như vậy, tổng số đoạn thẳng là
• Số cạnh của đa giác lồi là n
Suy ra số đường chéo của đa giác đều n đỉnh là:
Câu 36. Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được tạo ra từ các số khác 0 mà trong mỗi số luôn luôn có mặt hai chữ số chẵn và hai chữ số lẻ?
A.
B.
C.
D.
Đáp án: C
Giải thích:
Số cách chọn 2 số chẵn trong tập hợp {2; 4; 6; 8} là: 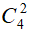
Số cách chọn 2 số lẻ trong tập hợp {1; 3; 5; 7; 9} là: 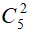
Số cách hoán vị 4 chữ số đã chọn lập thành 1 số tự nhiên là: 4! cách.
Vậy có 4!*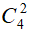
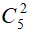
Câu 37. Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai màu.
A. 300
B. 310
C. 320
D. 330
Đáp án: B
Giải thích:
Các viên bi lấy ra có đủ cả 2 màu nên ta có các trường hợp:
Cách 2. Dùng phần bù. Số cách chọn 4 viên bi tùy ý từ 11 viên bi là: 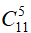
Số cách chọn 4 viên bi màu trắng là: 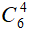
Số cách chọn 4 viên bi là màu xanh là: 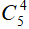
Vậy có 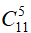
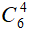
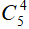
Câu 38. Từ 20 người cần chọn ra một đoàn đại biểu gồm 1 trưởng đoàn, 1 phó đoàn, 1 thư kí và 3 ủy viên. Hỏi có bao nhiêu cách chọn đoàn đại biểu ?
A. 4651200
B. 4651300
C. 4651400
D. 4651500
Đáp án: A
Giải thích:
Câu 39. Một nhóm đoàn viên thanh niên tình nguyện về sinh hoạt tại một xã nông thôn gồm có 21 đoàn viên nam và 15 đoàn viên nữ. Hỏi có bao nhiêu cách phân chia 3 nhóm về 3 ấp để hoạt động sao cho mỗi ấp có 7 đoàn viên nam và 5 đoàn viên nữ?
Đáp án: D
Giải thích:
Nhóm thứ 1: chọn 7 nam từ 21 bạn nam, chọn 5 nữ từ 15 bạn nữ nên số cách chọn nhóm thứ nhất là: 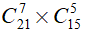
Nhóm thứ 2: chọn 7 nam từ 14 bạn nam còn lại, chọn 5 nữ từ 10 bạn nữ còn lại nên số cách chọn nhóm thứ hai là: 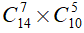
Số cách chọn nhóm thứ ba là: 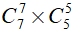
Vậy có 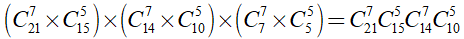
Câu 40. Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh trong số học sinh giỏi đó sao cho mỗi khối có ít nhất 1 học sinh?
A. 85
B. 58
C. 508
D. 805
Đáp án: D
Giải thích:
Số cách chọn 6 học sinh bất kì trong 12 học sinh là: 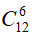
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 10 ( hay 6 học sinh từ khối 11 và 12) là: 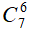
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 11 (hay 6 học sinh từ khối 10 và 12) là: 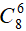
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 12 (hay 6 học sinh từ khối 10 và 11) là: 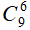
Vậy có 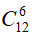
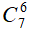
Các câu hỏi trắc nghiệm Toán lớp 11 có đáp án, chọn lọc khác:
Trắc nghiệm Nhị Thức Newton có đáp án
Trắc nghiệm Phép thử và Biến cố có đáp án
Trắc nghiệm Xác suất của biến cố có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án